条件故障下3-元n-立方体的容错分析

秦学姣

(新疆医科大学 厚博学院，新疆 克拉玛依 834000)

在设计一个互连网络时，容错性是一个基本原则，边连通性是衡量互连网络容错性的一个重要指标。图G的边连通度，记作λ(G)，定义为使G不连通时需删除的最小边数。然而，边连通度往往低估了多处理系统的容错能力。在很多情况下，当故障边数大于边连通度时，一个具有故障边的网络仍可能是连通的，或者存在较大的连通分支[1-3]。因此，互连网络的容错性与带有故障边的网络的较大连通分支的顶点数密切相关。

假设F是图G的一故障边集，G-F是从G中删除F得到的图,u和v是图G-F中的两个顶点，我们关心的是G-F中u和v之间的边不相交无故障路径的数目。我们将此问题考虑为边故障条件下的Menger定理[4]。近年来，学者们对互连网络的Menger特性进行了大量的研究[5-7]。特别地，Qiao等[6]研究了条件故障下的超立方体和折叠超立方体的强Menger边连通性。

k-元n-立方体是一类重要的互连网络。一方面，其包括了传统的互连网络作为其子类，如环(1-元n-立方体)、超立方体(2-元n-立方体)和环面(k-元 2-立方体)。另一方面，目前已经建立了多个大型并行分布式计算系统，如Gray T3D、J-machine、iWarp和Blue Gene，都是基于k-元n-立方体的拓扑结构。近年来，k-元n-立方体的许多拓扑性质得到了广泛的研究[8-13]。例如，Li等[9]考虑了路限制条件下将路和圈嵌入到3-元n-立方体中的问题；Yuan等[11]研究了3-元n-立方体网络的g-好邻点条件可诊断性。目前，有关条件故障下k-元n-立方体的强Menger性的研究较少。本文研究了具有条件边故障的3-元n-立方体网络的较大连通分支和强Menger边连通性。

1 预备知识

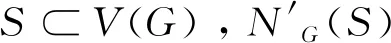
定义1[5]连通图G称为条件边故障下的f-强Menger连通度，是指在F⊂E(G),|F|≤f和δ(G-F)≥2条件下，G-F中任意一对顶点u和v之间存在min{degG-F(u),degG-F(v)}条边不交的无故障路。

2 带有故障边的3-元n-立方体的较大连通分支

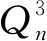
取(t+1)组3-元子立方体，其顶点集互不相交。用Qi代表第i组3-元子立方体，这里0≤i≤t。而每一个Qi包含xi个3-元yi-维子立方体，记做Qi,1,…，Qi,xi。

Qi,ji表示第ji个3-元yi-维子立方体，这里0≤i≤t,1≤ji≤xi≤2。G1可以用一种递归的方式得到。给定Q0,j0，其包含x0个3-元y0-维子立方体，在不产生歧义的时候，我们也使用U1U2…Uy0-1Uy0(j0-1)00…00来代表Q0,j0，3-元yi-维子立方体Qi,ji(i>0)是指Qi-1,xi-1把第(yi-1+1)位的(ji-1-1)改为xi-1，把Qi-1,xi-1的第(yi+1)位坐标改为(ji-1)而获得。除了第(yi-1+1)位坐标外，令第(yi+2)位坐标到第yi-1位坐标都是0。G1的构造如图1所示。

图1 G1的构造

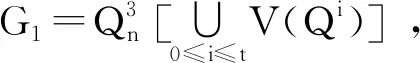
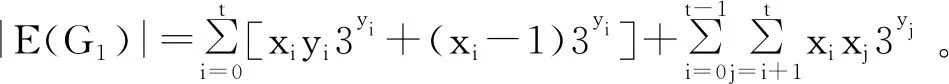
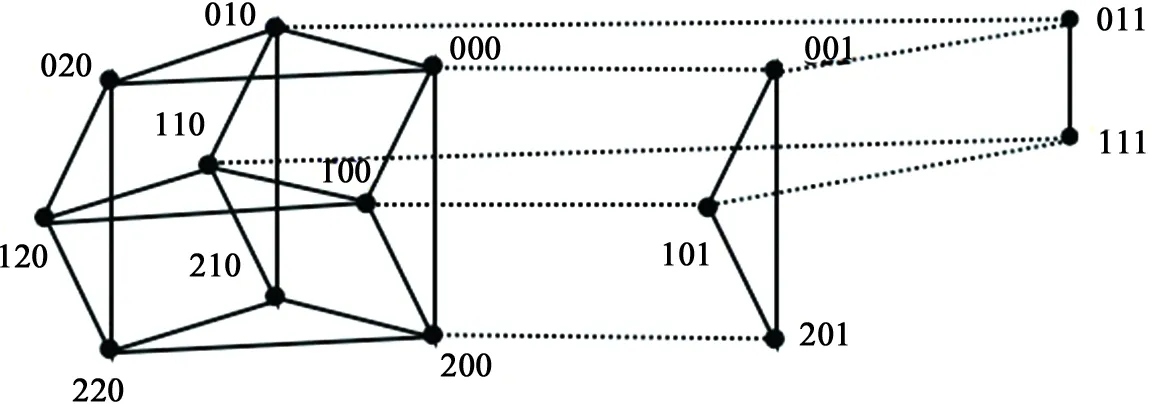
图的图示

为了方便理解这个构造的方法，下面举一个具体的例子(图2)：

构造如下：

Q0,j0,j0=1:U1U20；

Q1,j1,j1=1:U101；

Q2,j2,j2=1,2:011,111。

且V(G1)={000,100,200,010,110,210,020,120,220}∪{001,101,201}∪{011}∪{111}={000,100,200,010,110,210,020,120,220,001,101,201,011,111}。

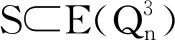
按照这个定理的结论，我们可以得到表1。

表1 带有故障边的的较大连通分支

3 带有条件边故障的的强Menger边连通度

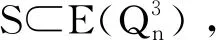
证明：使用数学归纳法来证明。当n=2时，引理结论显然成立。假设引理对n-1时结论成立。下面证明引理对n结论成立，这里n≥3。

情况1 |S2|≤4n-7

情形1.1 |S0|≤|S1|≤|S2|≤2n-3

情形1.2 |S0|≤|S1|≤2n-3且2n-2≤|S2|≤4n-7

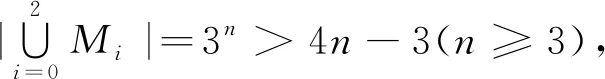
情形1.3 |S0|≤2n-3且2n-2≤|S1|≤|S2|≤4n-7

情况2 |S0|≤|S1|≤4n-7且4n-6≤|S2|≤4n-3

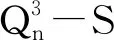
综上所述，引理得证。

注解3.2 引理3.1的结果是最优的。

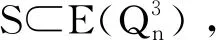
证明方法与引理3.1类似，故略。

注解3.4 引理3.3的结果是最优的。

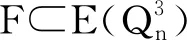
情况1 |V(H)|=3n-1

情况2 |V(H)|=3n-2

下面，证明这个结论是最优的。

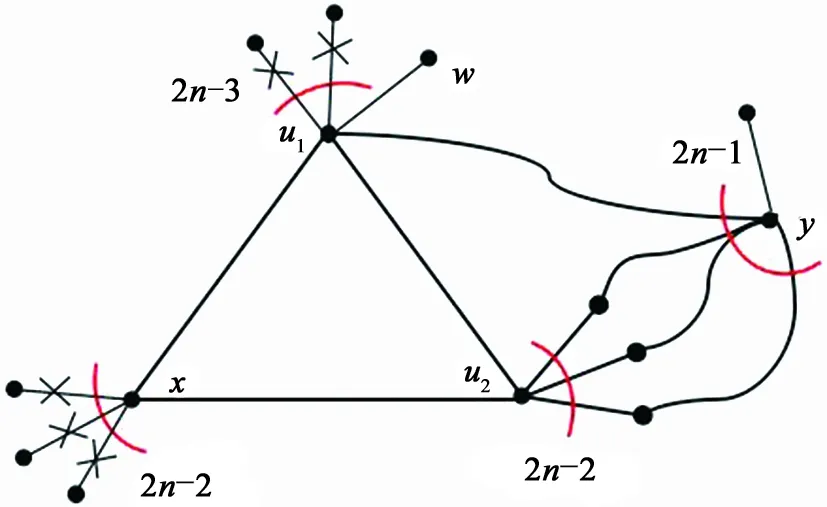
图3 定理3.5的图示Fig.3 Illustration for the Theorem 3.5