深孔弧形钢闸门支铰钢梁结构分析计算

黄臣勇，何 伟，李云峰

(贵州省水利水电勘测设计研究院有限公司，贵州 贵阳 550002)

对于布置在隧洞进口端的高水头弧形工作闸门，为方便安装和支铰找平通常采用在支铰后侧设置一根钢结构梁，支铰推力通过该梁传递给钢筋混凝土结构或基岩。在对该梁进行截面设计时因计算模型选择不当或考虑不周全都可能出现设计错误，造成安全隐患。本文以设计实例为基础就该梁计算常见的三种方法进行对比计算，并用ANSYS建立有限元模型进行验证。

1 工程概况

某工程泄洪洞弧形钢闸门孔口尺寸为5.5×6-74 m，总水压力为38005 kN，在启门力、自重和总水压力作用下单只支铰推力为19240 kN。闸门支铰支承在二期混凝土内的钢结构梁上，钢梁采用箱型截面，钢材采用为Q345C，钢箱梁宽1750 mm，高为1220 mm，上翼缘厚为60 mm，下翼缘(与混凝土接触)厚为40 mm，腹板厚30 mm，钢梁两端伸入闸墩侧墙各1000 mm，全程长为7500 mm，闸门布置形式见图1，钢箱梁截面见图2，截面几何参数见表1。

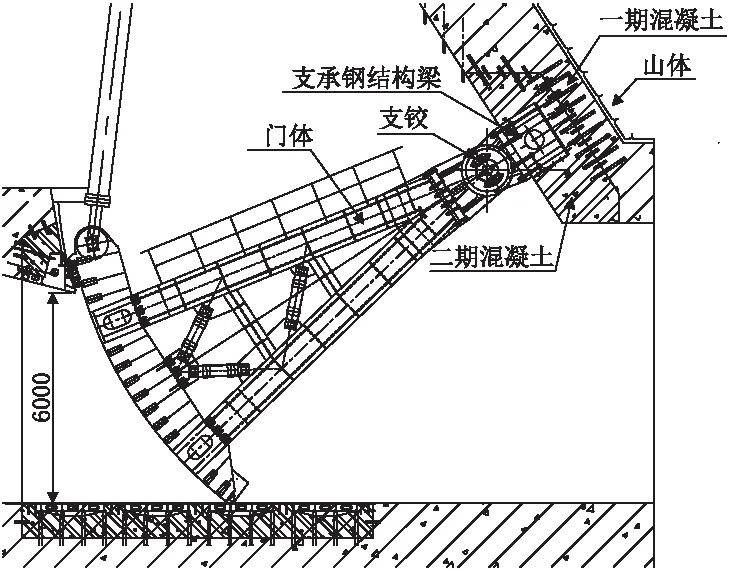
图1 闸门总图布置

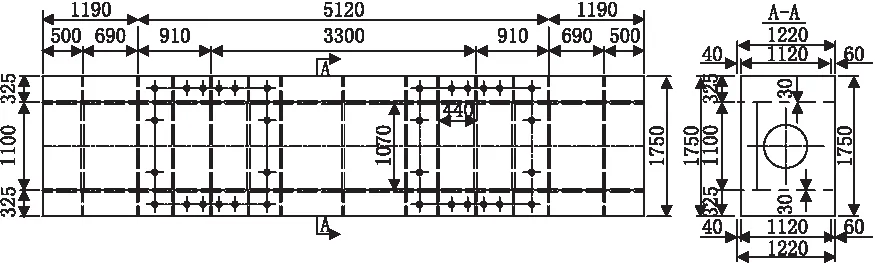
图2 钢结构梁截面

表1 钢箱梁几何参数表

2 三种计算方法验算计算

支铰钢梁计算方法常采用以下三种方法进行。①按钢结构柱脚底板计算，该计算方法主要计算与支铰座板接触面的上翼缘板厚度，其余按构造要求和满足局部稳定的方法确定腹板厚度和肋板间距；②采用倒梁法计算钢梁弯矩，该计算方法将支铰推力换算为线荷载作用在梁上，支铰位置假设为两个简支点，根据计算弯矩和剪力设计验算截面；③按弹性地基梁计算钢梁弯矩，该计算方法为文克尔有限元法，设计方式与倒梁法类似。

2.1 按柱脚底板计算

按钢结构柱脚底板计算方法确定钢梁上翼缘厚度，首先根据钢梁肋板分布确定计算区域。在荷载作用区域肋板将区隔划分为三边支承区域8个，四边固定区域4个。三边支承区和四边支承区边长最大区域为最不利分区，选取两个最不利区进行厚度计算。

三边支承区隔厚度计算：

区隔固定边长a=310 mm，自由边长度b=450 mm，a/b=0.775，查表得β=0.095。

弯矩计算：M=βσb2=0.095×7.07×4502=136009 N·mm

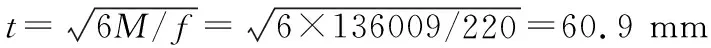
四边支承区隔厚度计算：

区隔长边a=1070 mm，短边长度b=450 mm，a/b=2.38，查表得β=0.125。

弯矩计算：M=βσb2=0.125×7.07×4502=178959 N·mm

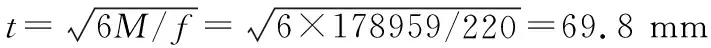
按柱脚板计算方式计算支铰钢梁上翼缘板厚应大于69.8 mm。该计算方法将钢梁假设为一个刚性无限大的支座，在受力过程中不发生变形，用该方法计算上翼缘板厚度较为保守也不合理，支铰座板已经按柱脚底板计算方法确定厚度，支铰底板有足够刚度，可以限制钢梁上翼缘的变形，可均匀将荷载传递到钢梁腹板和肋板上。

该计算方法未整体考虑梁的受力情况，对传递荷载起关键作用的腹部、下翼缘等构件未进行受力计算，采用该方法计算不够全面，建议不采用。

2.2 按倒梁法计算

作用在支铰钢梁上的两个推力大小相等，间距较小，且为对称布置，传递荷载的闸门支臂刚度较大，支铰钢梁的受力方式与条形基础相同，采用倒梁法计算钢梁内力是比较符合实际情况的。基底反力假设按均匀线性分布，钢梁按倒梁法计算模型为一跨双悬臂连续梁，梁中间跨度为L1=3.2 m，悬臂端长L2=2.1 m，均布线荷载为q=5130.67 kN/m。

支座位置弯矩计算：M=q×L22/2=5130.67×2.12/2=11313.2 kN/m。

支座位置剪力计算：T=q×L2=5130.67×2.1=10774.4 kN。

跨中位置弯矩计算：M=5130.67×(3.3/2+2.1)2/2-19240×3.2/2=4329 kN·m。

跨中位置剪力计算：T=19240-10774.4=8465.6 kN。

支座位置为最不利截面，该截面验算如下：

弯应力计算：σ=Mmax/Wxmin=11313200000/94865853=119.5 N/mm2

剪应力计算：τ=T×Sx/(Ix×tw)=10774400×59373484/(65281964663×60)=163 N/mm2

按倒梁法计算支铰钢梁受剪力控制，剪应力不满足规范要求。

2.3 按弹性地基梁计算

支铰钢梁在受力过程中会与混凝土之间变形协调一致，钢梁与基础混凝土始终保持接触不出现分离现象；在支铰推力和基础反力处于静力平衡状态，支铰钢梁满足弹性地基梁计算假设的两个基本条件。采用弹性地基梁假设对支铰钢梁进行内力分析也是合理的。弹性地基梁计算过程复杂，随着计算机软件的发展通用有限元软件均可完成相关计算。本文采用SAP2000通用有限元软件进行内力计算。基础弹簧刚度按钢筋混凝土结构取7490 kN/m。计算弯矩和剪力见图3和图4，最大弯矩M=9566.2 kN·m，对应剪力Q=1022.2 kN；最大剪力Q=7378.6kN，对应位置弯矩为M=5376.2 kN·m。

图3 弯矩图

图4 剪力图

弯矩最大截面验算：

弯应力计算：σ=Mmax/Wxmin=956620000、94865853=100.8 N/mm2

剪应力计算：τ=T×Sx/(Ix×tw)=1022200×59373484/(65281964663×60)=15.4 N/mm2

剪力最大截面验算：

弯应力计算：σ=Mmax/Wxmin=5376200000/94865853=56.7 N/mm2

剪应力计算：τ=T×Sx/(Ix×tw)=7378600×59373484/(65281964663×60)=111.8 N/mm2

按弹性地基梁计算钢梁各项应力满足规范要求。

3 有限分析计算

3.1 有限计算模型

采用ANSYS有限元软件对支铰钢梁和梁后混凝土建立整体模型进行分析。模型中支铰钢梁采用shell63单元，材料为Q345B低合金钢，弹性模量E为206 GPa，泊松比为0.3，其容许应力为[σ]=220 MPa，[τ]=130 MPa；混凝土采用sold45单元，混凝土结构强度等级为C40，弹性模量E为0.325 GPa，泊松比为0.2，承压容许应力[σ]=14 MPa。在对钢梁和混凝土单元进行网格划分时两个接触面网格划分一致，节点通过耦合连接在一起。支铰推力换算为面荷载施加在闸门支座作用面上，混凝土后表面所有节点约束6个自由度。为使计算结果尽可能精确钢梁采用四边形网格划分，混凝土结构采用六面体网格划分，共划分159530个单元，594598个节点。

3.2 计算结果

通过有限元分析提取钢梁变形、弯应力、剪应力、混凝土表面应力分布等主要数据见图5～图9。

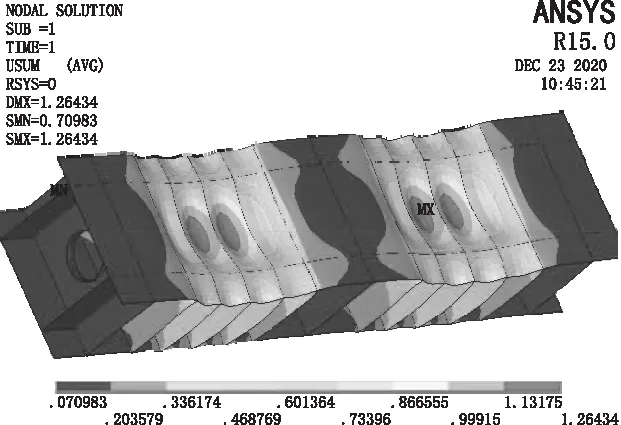
图5 钢梁变形云图

图6 钢梁剪应力分布云图

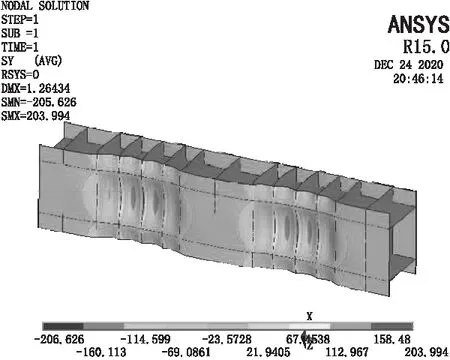
图7 钢梁弯应力分布云图

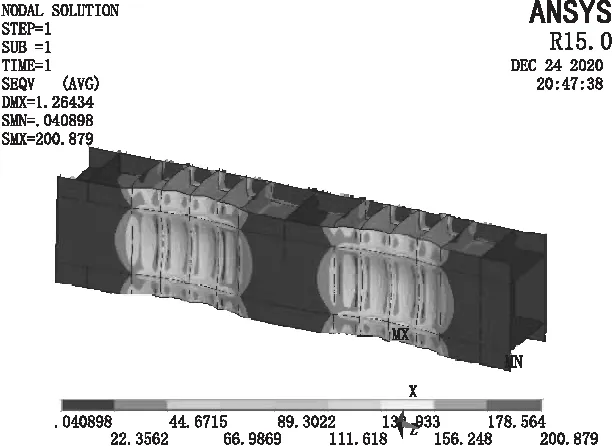
图8 钢梁折算应力分布图

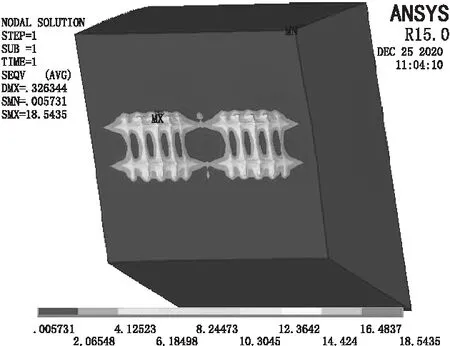
图9 混凝土表面压应力分布

根据有限元计算分析结果显示钢梁各项应力均满足规范要求的容许应力值，钢梁与混凝土接触面存在压应力超过混凝土容许承压值的情况。

4 计算结果对比分析

本例采用柱脚底板验算、倒梁法验算、弹性地基梁法三种方法进行验算，并采用ANSYS有限元软件进行复核。采用柱脚底板验算方法不能全面反映该梁的受力特征就不列入对比，故对其余三种方法计算结果进行对比，对比结果见表2。

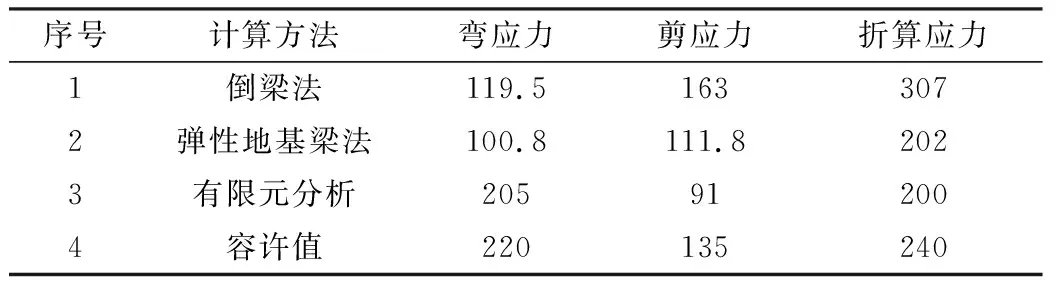
表2 计算结果对比 单位：N/mm2

通过对比发现三种计算方法均能反应钢梁的受力情况，倒梁法是一种保守计算方法，在不考虑基础变形对应力的释放，计算结果偏安全。弹性地基梁法和ANSYS分析计算都属于有限元计算，这两种方法计算结果比较接近(扣除ANSYS中应力集中点)，能真实反映实际受力情况。

采用ANSYS分析还显示基础混凝土承压应力达到18.5 MPa，超过容许值，这是其余两种计算方法不能反映的；当腹板和肋板将荷载传递到下翼缘时，下翼缘板厚度较小时，刚度不足，下翼缘发生弯曲变形，与混凝土接触面变小，导致局部承压应力超标。将下翼缘厚度调整为70 mm后混凝土承压应力计算结果见图10。当钢梁下翼缘厚度增大，刚度变大后混凝土面承压应力为12.6 MPa。通过调整下翼缘厚度对比计算分析，钢梁与混凝土接触面翼缘厚度采用柱脚板验算方法进行厚度复核是有必要和合理的。

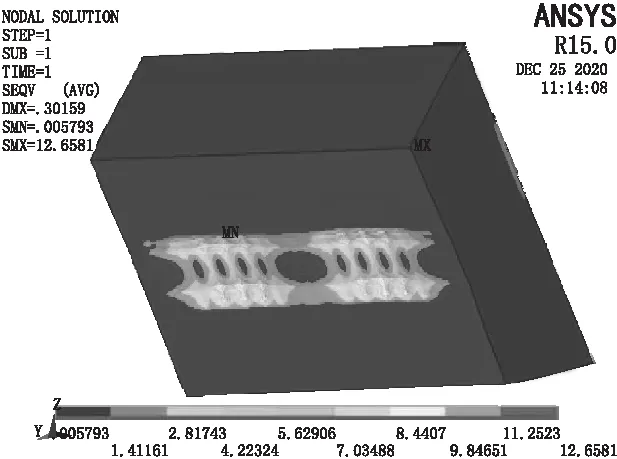
图10 混凝土承压应力分布土

通过对比分析计算可知本例支铰钢梁截面设置不合理，钢梁上翼缘厚度较大，下翼缘厚度不足，将钢梁上翼缘厚度调整为40 mm，下翼缘厚度调整为70 mm，截面各项指标均满足规范要求。

5 结论

深孔弧形闸门为方便安装如设置支撑钢梁，且钢梁埋入混凝土结构中，在对钢梁进行设计应对截面强度进行验算，且与混凝土接触面的翼缘板应按钢结构中柱脚底板计算方法对厚度进行复核，防止混凝承压应力超标。截面强度验算采用弹性地基梁法或有限元分析可以更真实地反映梁的受力情况，减小板件的厚度为制作和安装提供方便。