伪核逆的广义Cline公式和广义Jacobson引理
2021-08-18管健行宋贤梅李明珠
管健行,宋贤梅,李明珠
(安徽师范大学 数学与统计学院,安徽 芜湖 241002)
引言

Cline[7]证明了环中若ab是Drazin可逆的,则ba是Drazin可逆的。此时(ba)D=b[(ab)D]2a,称之为Cline公式。Liao[8]证明了Cline公式适用于广义Drazin逆。近几年,许多学者对Cline公式也进行了各种形式的推广。Zeng[9]研究在dbd=acd,aca=dba条件下广义逆的Cline公式。Chen[10]研究环中Drazin逆,广义Drazin逆,伪Drazin逆在dbd=acd,bdb=bac条件下的Cline公式。Shi等[6]研究了当ab有伪核逆,则ba有伪核逆的充分必要条件。
受此启发,本文研究了在dbd=acd,bdb=bac条件和dbd=acd,aca=dba条件下伪核逆的广义Cline公式和广义Jacobson引理。为了简便,我们将条件dbd=acd,bdb=bac记为条件1,条件dbd=acd,aca=dba记为条件2。文中的第二部分,我们给出了在条件1下ac是伪核可逆,则bd是伪核可逆的充分必要条件,且由ac的伪核逆给出了bd的伪核逆。第三部分研究了在条件2下ac(或bd)是伪核可逆,则bd(或ac)是伪核可逆的充分必要条件,且由ac(或bd)的伪核逆给出了bd(或ac)的伪核逆。第四部分我们给出了在条件1下1-ac是伪核可逆,则1-bd是伪核可逆的充分必要条件,且由1-ac的伪核逆给出了1-bd的伪核逆。第五部分,我们给出了在条件2下1-ac(或1-bd)是伪核可逆,则1-bd(或1-ac)是伪核可逆的充分必要条件,且由1-ac(或1-bd)的伪核逆给出了1-bd(或1-ac)的伪核逆。
最后,为了讨论的方便,给出文中需要的定义与符号。
设R是有单位元的结合环,若存在映射*:R→R使得对所有的x,y∈R,均满足(1)(x+y)*=x*+y*,(2)(xy)*=y*x*,(3)(x*)*=x,则称R是*-环。
定义1[11]a∈R是伪核可逆当且仅当存在x∈R满足下列条件:
(1)xam+1=am,整数m≥1;(2)ax2=x;(3)(ax)*=ax。
若这样的x存在,则它是唯一的且称之为a的伪核逆(记为a)。
定义2[11]a∈R是对偶伪核可逆当且仅当存在y∈R满足下列条件:
(1)am+1y=am,整数m≥1;(2)y2a=y;(3)(ya)*=ya。
若这样的y存在,则它是唯一的且称之为a的对偶伪核逆(记为a)。
环R中伪核可逆元素的集合记为R,对偶伪核可逆元素的集合记为R。记α(1,3)是α的{1,3}逆,α(1,4)是α的{1,4}逆。
1 伪核逆在条件1下的Cline公式
[6]中的定理4.5研究了当ab是伪核可逆,则ba是伪核可逆的充分必要条件是b(ab)Da∈R{1,3}。同样地,本节讨论了在条件1下当ac是伪核可逆,则bd是伪核可逆的充分必要条件是b(ac)Dd∈R{1,3}。
引理1.1设a,b,c,d∈R,满足条件1。若α=ac∈RD,则β=bd∈RD。此时,βD=b(αD)2d。
证明: 令x=b(αD)2d,易知
b(αD)2dbd=b(αD)2acd=bαDd,b(αD)2dbdb(αD)2d=b(αD)2dbd。因为b(αD)2dbdb(αD)2d=bαDdb(αD)2d,又因为αD与ac可交换,由dbac=dbdb=acdb知αD与db可交换,所以
b(αD)2dbdb(αD)2d=bαDdb(αD)2d=b(αD)2d
此外,
(bd)k+2b(αD)2d=b(ac)k+1db(αD)2d=b(ac)k+1(αD)2acd=b(ac)kd=(bd)k+1,
因此,bd是Drazin可逆,且βD=b(αD)2d。
引理1.2[6,引理3.1]设a∈R且I(a)=m,则:
(1)aa=ak(a)k,任意的整数k≥1;
(2)aaa=a;
(3)ak(a)kak=ak,任意的整数k≥1;
(4)a∈RD且i(a)=m,同时,aD=(a)m+1am。
引理1.3[6,定理3.3]若a∈RD,则下列条件等价:
(1)a∈R;
(2)aa∈R{1,3};
(3)aπ∈R{1,4}。
此时,aaD∈(aaD){1,3},(1-aa)∈aπ{1,4},且
a=aD(aaD)(1,3)=aD(1-(aπ)(1,4)aπ),
对任意的(aaD)(1,3)∈(aaD){1,3}和(aπ)(1,4)∈aπ{1,4}。
引理1.4[6,定理3.4]若a∈RD,则下列条件等价:
(1)a∈R;
(2)aaD∈R{1,4};
(3)aπ∈R{1,3}。
此时,aa∈(aaD){1,4},1-aa∈aπ{1,3},且
a=(aaD)(1,4)aD=(1-aπ(aπ)(1,3))aD,
对任意的(aaD)(1,4)∈(aaD){1,4}和(aπ)(1,3)∈aπ{1,3}。
定理1.5设a,b,c,d∈R,满足条件1。若ac∈R,则bd∈R当且仅当b(ac)Dd∈R{1,3}。此时,(bd)=b((ac)D)2d(b(ac)Dd)(1,3)。
证明令α=ac,β=bd。因为α=ac∈R,由引理1.2知α∈RD,根据引理1.3知ααD∈R{1,3}。
由引理1.1可知,β∈RD且βD=b(αD)2d。因为
ββD=bdb(αD)2d=bac(αD)2d=bαDd,
所以由引理1.3知β∈R⟺bαDd∈R{1,3}。此时,对于任意的(bαDd)(1,3)∈(bαDd){1,3},有
β=βD(ββD)(1,3)=b(αD)2d(bαDd)(1,3)
注1.6若α∈R,由引理1.2知α∈RD且αD=(α)k+1αk,其中I(α)=k,定理1.5中的β可写为:
β=b((α)k+1αk)2d(bαDd)(1,3)。
定理1.7设a,b,c,d∈R,满足条件1。若ac∈R,则bd∈R当且仅当b(ac)Dd∈R{1,4}。此时,(bd)=(b(ac)Dd)(1,4)b((ac)D)2d
证明令α=ac,β=bd,因为α=ac∈R,由引理1.2知α∈RD。根据引理1.1可知,β∈RD且βD=b(αD)2d。
因为β∈RD和ββD=bαDd,所以由引理1.4知
β∈R⟺bαDd∈R{1,4}。
此时,对于任意的(ββD)(1,4)∈(ββD){1,4},有
β=(bαDd)(1,4)b(αD)2d=(b(ac)Dd)(1,4)b(ac)D)2d。
注1.8由注1.6,知αD=(α)k+1αk,所以定理1.7中的β可写为:
β=(bαDd)(1,4)b(α)k+1αk)2d
2 伪核逆在条件2下的Cline公式
本节主要研究了在条件2下当ac(或bd)是伪核可逆,则bd(或ac)是伪核可逆的充分必要条件。
引理2.1[9,定理2.1]设a,b,c,d∈R,满足条件2。则ac∈RD⟺bd∈RD。此时,(ac)D=d((bd)D)3bac和(bd)D=b((ac)D)2d。
定理2.2设a,b,c,d∈R,满足条件2。若bd∈R,则ac∈R当且仅当d((bd)D)2bac∈R{1,3}。
此时,(ac)=d((bd)D)3bac[d((bd)D)2bac](1,3)。
证明令α=ac,β=bd。因为β=bd∈R,由引理1.2知β∈RD,根据引理1.3知ββD∈R{1,3}和ββ∈(ββD){1,3}。
由引理2.1可知,α∈RD且αD=d(βD)3bac。因为ααD=acd(βD)3bac=dbd(βD)3bac=d(βD)2bac,所以由引理1.3知ac∈R⟺d((bd)D)2bac∈R{1,3}。
此时,对于任意的(d(βD)2bac)(1,3)=d(βD)2bac{1,3},由引理1.3有
α=αD(ααD)(1,3)=d(βD)3bac(d(d(βD)2bac)(1,3)。
定理2.3设a,b,c,d∈R,满足条件2。若ac∈R,bd∈R当且仅当b(ac)Dd∈R{1,3}。此时,(bd)=b((ac)D)2d(b(ac)Dd)(1,3)。
证明与定理2.2类似。
定理2.4设a,b,c,d∈R,满足条件2。若bd∈R,则ac∈R当且仅当d((bd)D)2bac∈R{1,4}。
此时,(ac)=(d((bd)D)2bac)(1,4)d((bd)D)3bac
证明:令α=ac,β=bd,因为α=ac∈R,由引理1.2知β∈RD。根据引理2.1可知,α∈RD且αD=d(βD)3bac。
因为ααD=acd(βD)3bac=dbd(βD)3bac=d(βD)2bac,所以由引理1.4知,ac∈R⟺d((bd)D)2bac∈R{1,4}。
此时,对于任意的(d((bd)D)2bac)(1,4)∈d((bd)D)2bac{1,4},有
(ac)=(ac(ac)D)(1,4)(ac)D=(d((bd)D)2bac)(1,4)d((bd)D)3bac。
定理2.5设a,b,c,d∈R,满足条件2。若ac∈R,则bd∈R当且仅当b(ac)Dd∈R{1,4}。此时,(bd)=(b(ac)Dd)(1,4)b((ac)D)2d
证明与定理2.4相类似。
3 伪核逆在条件1下的Jacobson引理
[6]研究了1-ab是伪核可逆,则1-ba是伪核可逆的充分必要条件,且由1-ab的伪核逆给出了1-ba的伪核逆。本节给出了在条件1下,1-ac是伪核可逆,则1-bd是伪核可逆当且仅当b(1-ac)πrd∈R{1,4}。
定理3.1设a,b,c,d∈R,满足条件1。若1-ac∈R,则1-bd∈R当且仅当b(1-ac)πrd∈R{1,4}。其中r=1+(1-ac)+…+(1-ac)k-1。此时,
(1-bd)=(1+b(1-ac)Dd)[1-(b(1-ac)πrd)(1,4)b(1-ac)πrd]。
证明令α=1-ac,β=1-bd,I(α)=k。因为1-ac∈R,由引理1.2知α∈RD且i(α)=k。由引理1.3知απ∈R{1,4},所以根据[4,定理2.3],可知β∈RD且βD=1+bαDd-bαπrd,其中r=1+(1-ac)+…+(1-ac)k-1。所以
βπ=1-ββD
=1-(1-bd)(1+bαDd-bαπrd)
=1-(1-bd)-(1-bd)bαDd+(1-bd)bαπrd
=bd-bαDd+bdbαDd+bαπrd-bdbαπrd
=bαπrd+b[1-αD+(1-α)αD-(1-α)απr]d
=bαπrd+b[1-ααD-(1-α)απr]d
=bαπrd
因此,由引理1.3可得β∈R⟺βπ=b(1-ac)πrd∈R{1,4}。
此时,对于任意的(βπ)(1,4)∈βπ{1,4},由引理1.3可得
β=βD[1-(βπ)(1,4)βπ]。
又因为βD=1+bαDd-bαπrd=(1+bαDd)(1-bαπrd),则
β=βD[1-(βπ)(1,4)βπ]
=(1+bαDd)(1-bαπrd)[1-(bαπrd)(1,4)bαπrd]
=(1+bαDd)[1-(bαπrd)(1,4)bαπrd]
注3.2若α∈R,由引理1.2知α∈RD且αD=(α)k+1αk,其中I(α)=k。此时定理3.1中的β可写为:
β=(1+b(α)k+1αkd)[1-(bαπrd)(1,4)bαπrd]
若令定理3.1中I(1-ab)=1, 我们有下面的推论:
推论3.3设a,b,c,d∈R,满足条件1。若α=1-ac∈R,β=1-bd∈R当且仅当b(1-ac)πd∈R{1,4}。
此时,β=(1+bα#d)[1-(bαπd)(1,4)bαπd]。
定理3.4设a,b,c,d∈R,满足条件1。若α=1-ac∈R,则β=1-bd∈R当且仅当b(1-ac)πrd∈R{1,3}。其中r=1+(1-ac)+…+(1-ac)k-1。
此时,(1-bd)=(1-b(1-ac)πrd(b(1-ac)πrd)(1,3))(1+bαDd)。
证明:因为α∈R,由引理1.2知α∈RD且i(α)=k。根据[4,定理2.3],可知β∈RD且βD=1+bαDd-bαπrd,其中r=1+(1-ac)+…+(1-ac)k-1。此外,我们知βπ=bαπrd。因此,由引理1.4可得β∈R⟺bαπrd∈R{1,3}。
此时,对任意的(βπ)(1,3)∈βπ{1,3},有β=(1-βπ(βπ)(1,3))βD,则
β=[1-bαπrd(bαπrd)(1,3)](1+bαDd)(1-bαπrd)
=(1-bαπrd(bαπrd)(1,3))(1+bαDd)
4 伪核逆在条件2下的Jacobson引理
本节研究了在条件2下当ac(或bd)是伪核可逆,则bd(或ac)是伪核可逆的充分必要条件。
定理4.1设a,b,c,d∈R,满足条件2。若1-ac∈R,则1-bd∈R当且仅当bac(1-ac)πr′d∈R{1,4}。
其中r′=1+(1-acac)+…+(1-acac)k-1。此时
β=(1+bacαDd+bd)[1-(bac(1-ac)πr′d)(1,4)bac(1-ac)πr′d]
证明:令α=1-ac,β=1-bd,I(α)=k。因为1-ac∈R,由引理1.2知α∈RD且i(α)=k。由引理1.3知απ∈R{1,4},所以由[5,定理3.1]知β=1-bd∈RD和βD=βn(1+bd+bacαDd)n+1,所以ββD=βn+1(1+bd+bacαDd)n+1=(1-bacαπd)n+1。
由Drazin逆的唯一性知当n≥k时,(1-bacαπd)n都相等。因此ββD=(1-bacαπd)k+1=(1-bacαπd)k。从而
βπ=1-ββD=1-(1-bacαπd)k=bacαπd[1+(1-bacαπd)+…+(1-bacαπd)k-1]。
因为d(1-bacαπd)=d-dbacαπd=d-acacαπd=(1-acacαπ)d,且απac=acαπ,所以
απd(1-bacαπd)i=απ(1-απacac)id=(απ-απacac)id=απ(1-acac)id。
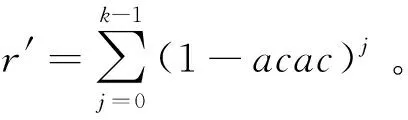
因此,由引理1.3知β∈R⟺βπ=bacαπr′d∈R{1,4}。此时,对于任意的(βπ)(1,4)∈βπ{1,4},由引理1.3有β=βD[1-(βπ)(1,4)βπ]。根据[5,定理3.1],知
βD=(1-bacαπr′d)(1+bd)+bacαDd=(1+bd+bacαDd)(1-bacαπr′d)。
因此,
βD=βD[1-(βπ)(1,4)βπ]
=(1+bd+bacαDd)(1-bacαπr′d)[1-(bacαπr′d)(1,4)bacαπr′d]
=(1+bd+bacαDd)[1-(bacαπr′d)(1,4)bacαπr′d]
定理4.2设a,b,c,d∈R,满足条件2。若1-bd∈R,则1-ac∈R当且仅当d(1-bd)πrbac∈R{1,4}。
其中r=1+(1-bdbd)+…+(1-bdbd)k-1。此时
(1-ac)=(1+d(1-ac)Dbac+ac)[1-(d(1-bd)πrbac)(1,4)d(1-bd)πrbac]。
证明与定理4.1证明类似。
注4.3由引理1.2知,若α∈R,则α∈RD,且αD=(α)k+1αk。其中I(α)=k。因此定理4.1中的β可表示为:
β=(1+bd+bac(α)k+1αkd)[1-(bacαπr′d)(1,4)bacαπr′d]。
类似地,α=(1+ac+d(β)k+1βkbac)[1-(dβπrbac)(1,4)dβπrbac]。
定理4.4设a,b,c,d∈R,满足条件2。若1-ac∈R,则1-bd∈R当且仅当bacαπr′d∈R{1,3}。
其中r′=1+(1-acac)+…+(1-acac)k-1。此时,
(1-bd)=[1-bacαπr′d(bacαπr′d)(1,3)](1+bd+bacαDd)。
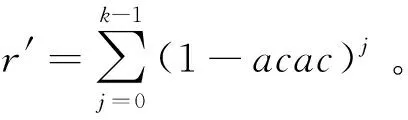
此时,对于任意的(βπ)(1,3)∈βπ{1,3},由引理1.4有β=(1-βπ(βπ)(1,3))βD。因此
β=[1-bacαπr′d(bacαπr′d)(1,3)](1+bd+bacαDd)(1-bacαπr′d)
=[1-bacαπr′d(bacαπr′d)(1,3)](1+bd+bacαDd)。
