针对轨道车辆走行部关键部件故障的智能识别研究
2021-08-17周宏祥尧辉明
周宏祥 尧辉明
摘 要:针对轨道车辆走行部关键部件的故障识别问题,本文提出了利用蚁群算法对弹簧的状态参数进行估计。通过对轨道车辆横向动力学方程建立的多元线性回归模型进行处理,得到约束模型。利用蚁群算法的寻优特性,在弹簧的正常、轻微故障和断裂的情况下对约束模型进行寻优计算,验证该算法的有效性。结果表明:该方法可以有效准确地估计轨道车辆走行部关键部件弹簧的实际参数值。通过比较估计值和正常值,可及时判断弹簧的状态,该参数估计方法可为轨道车辆悬挂系统关键部件状态监测提供重要的理论依据。
关键词:轨道车轮;动力学模型;蚁群算法;参数估计;寻优处理
中图分类号:TP391 文献标识码:A DOI:10.3969/j.issn.1003-6970.2021.03.024
本文著录格式:周宏祥,尧辉明.针对轨道车辆走行部關键部件故障的智能识别研究[J].软件,2021,42(03):086-089+102
Research on Intelligent Recognition of Failures of Key Components of Rail Vehicle Running Parts
ZHOU Hongxiang, YAO Huiming
(School of Urban Rail Transit, Shanghai University of Engineering Science, Shanghai 201620)
【Abstract】:Aiming at the problem of fault identification of the key components of the running part of rail vehicles, this paper proposes the use of ant colony algorithm to estimate the state parameters of the spring. By processing the multiple linear regression model established by the rail vehicle lateral dynamics equation, the constraint model is obtained. Using the optimization characteristics of the ant colony algorithm, the constraint model is optimized under the condition of normal, minor failure and breakage of the spring to verify the effectiveness of the algorithm. The results show that the method can effectively and accurately estimate the actual parameter values of the springs of the key components of the running gear of rail vehicles. By comparing the estimated value with the normal value, the state of the spring can be judged in time. This parameter estimation method can provide an important theoretical basis for the state monitoring of the key components of the rail vehicle suspension system.
【Key words】:rail wheel;dynamic model;ant colony algorithm;parameter estimation;optimization processing
0引言
目前,信号分析的方法是悬挂系统在线监测主要使用的方法,轨道车辆悬挂系统关键部件的幅值、频率特性以及对动力学参数的统计特征等关键部件的检测信号特性的突变是信号分析方法的主要研究对象,同时需要将较多的传感器安装在轨道车辆走行部的指定位置处。但是监测结果精度较低,有一定的局限性[1]。
相对于信号分析方法而言,参数估计以可操作性强等优点逐渐被广泛应用于故障状态监测领域中,为了达到估计轨道车辆关键部件的实际参数值的目的,仅需要通过安装在轨道车辆上的传感器获取车辆振动的信息,通过运算处理即可。文献[2]提等人通过采用粒子滤波算法对城市轨道交通车辆走行部关键部件参数进行仿真分析,验证了粒子滤波的参数估计算法能有有效的对车辆参数进行预测,有一定的工程应用价值。文献[3]利用率振动加速度的评判方法在对车轮缺陷的频率特征进行分析时,针对车轮的缺陷搭建车轮信息的数据采集装置进行分析但是工程可用性低。在利用算法进行参数估计时,算法自身的缺陷也会导致参数估计的结果精度低等问题,它们不能收敛到全局最优解,并且与初始值具有相关性。
针对上述问题,本文建立轨道车辆系统横向状态空间模型,针对对算法初始值要求过高以及因参数优化不能收敛到全局最优解的问题,提出利用蚁群算法为研究轨道车辆走行部关键部件弹簧的参数估计提供了一种较为理想的解决方案。
1 轨道车辆系统横向状态空间模型
1.1 参数估计模型
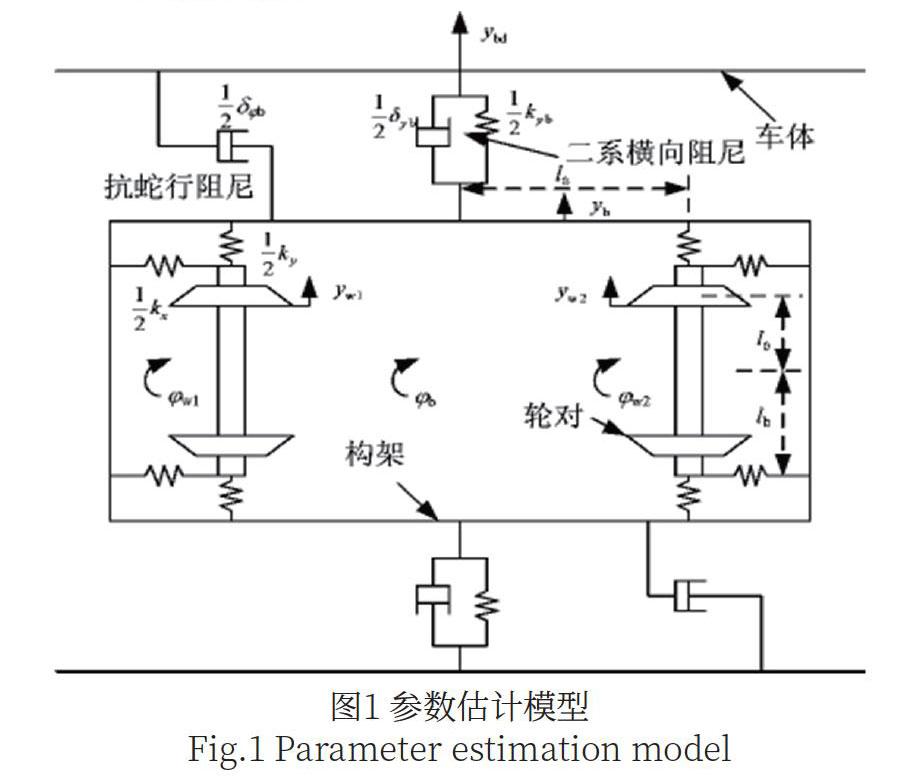
如图1所示的轨道车辆参数估计模型示意图[4],针对模型中示出的部分车体模型主要包括:轨道车辆走行部轮对,1个横向运动的自由度和构架均有横向和摇头运动的2个自由度。
图中:参数yw1和yw2分别为2个轮对的横向位移;参数yb表示为构架的横向位移;参数ybd表示为车体的横向位移;参数kx是一系纵向刚度;参数和分别为2个轮对的摇头角;参数表示为构架的摇头角;参数ky表示为横向刚度;参数kyb表示为二系横向刚度;参数l0表示为轨距的一半;参数la表示为转向架轴距的一半;参数lb为一系悬挂横向跨距的一半[5];参数δyb表示为二系横向阻尼;参数分别为和抗蛇行阻尼。
该参数估计模型的振动方程包括
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
式中:2个轮对处的轨道横向不平顺用yt1和yt2分别进行表示;2个轮对在轮轨接触点处的横向位移yd1和yd2分别进行表示;mw1和mw2分别为2个轮对的质量;构架和车体的质量用mb和mbd分别进行表示;纵向和横向蠕滑系數用f11和f22分别进行表示;2个轮对的转到惯量用Iw1和Iw2分别进行表示;构架转动惯量用Ib进行表示;轮对等效锥度用λ进行表示;车轮滚动半径用r0进行表示。
1.2 轨道车辆系统横向状态空间模型
把轨道车辆系统的横向参数估计模型中的振动方程变化为动态空间的方程如下。
(10)
(11)
其中,
w=,。
式中:参数w表示为信息反馈状态噪声,也就是轨道横向不平顺;参数为16×16型的矩阵;参数为16×2型的矩阵;参数H为5×16型的矩阵,可以由矩阵得到。
因式(10)为时间t的连续函数,因此使其离散后可得[6]
(12)
设Ts为采样时间间隔,在初始时刻t0=kTs的状态为x(kTs),则t=(k+1)Ts时刻的状态可以表示为
(13)
其中,
(14)
在时间区间[kTs,(k+1)Ts],当Ts足够小,w(τ)可以近似为常数w(kTs),则式(14)变换为
(15)
式中:I为16×16型的单位矩阵。
将式(15)代入式(13)可得
(16)
令,,,由上可得系统的横向动态空间模型为
(17)
(18)
2 蚁群算法在参数估计中的应用
蚁群算法的基本思路是在蚁群算法中,将单只蚂蚁理解为待估计的参数组合,是模型参数估计问题中的一个最优候选解,个体的维数就代表着待估计的参数个数p+1,设蚁群数为m,那么蚁群中第i个蚂蚁个体的位置可以表示为:
另外,求适值函数最小值的优化问题,通过蚁群算法进行处理[7]。
(19)
首先,将单只蚂蚁理解为待估计的参数组合,是模型参数估计问题中的一个最优候选解,个体的维数就代表着待估计的参数个数p+1,设蚁群数为n,那么蚁群中第i个蚂蚁个体的位置可以表示为:
。
选取适当的,使得最小。
基本实现步骤如下所示:
(1)初始化蚁群算法中的各项参数,对蚁群中蚂蚁的位置进行初始化;
(2)根据路径信息和初始参数信息,计算状态转移概率,增加随机性和遍历性,避免陷入局部最优,计算适应度函数值,设为初始信息素,计算状态转移概率;
(3)蚂蚁向最优解转移,单次行程结束后更新信息素;
(4)记录当前蚂蚁的最优位置;
(5)不断迭代,最终找到最优路径。
3 仿真计算
采用蚁群计算法对内容进行了详细的研究。本文将经过处理后的美国六级轨道谱的时域信号作为外部激励,输送到轨道车辆的参数估计模型之中。与此同时会得到振动响应数据,然后利用轨道车辆的动力学方程对弹簧刚度K和阻尼C进行求解,将获取的弹簧刚度K的值和阻尼C的值与参数估计模型的设定值进行比较,根据两者的差值大小来判断此时参数估计模型中,对应参数的关键部件的状态。由于一些因素的影响,需要对获取的数据进行处理,去除一些不符合实际的数据,本文采取200个正常状态下弹簧刚度和阻尼的结果数据如图2、图3所示:
当在仿真实验中获取到一些正常状态下的弹簧的横向刚度时,需要通过蚁群算法对抽选的数据进行优化处理,对轨道车辆的参数模型中的关键部件参数进行估计计算的本质上是探究最小解的过程。通过利用蚁群算法所得到的估计值和真实设定值之间的误差大小,来判断对应参数的关键部件的故障程度。其中在轨道车辆的参数估计模型中,将参数估计模型中关键部件Ky设置成368MN/m,Cy设置成12000N·s/m,轨道车辆走行部关键部件处于正常使用的状态下,利用蚁群算法对弹簧刚度进行寻优计算后,横向悬挂弹簧刚度Ky的参数值为385.44MN/m,如图4所示。横向阻尼Cy的值为11519.4N·s/m,如图5所示。
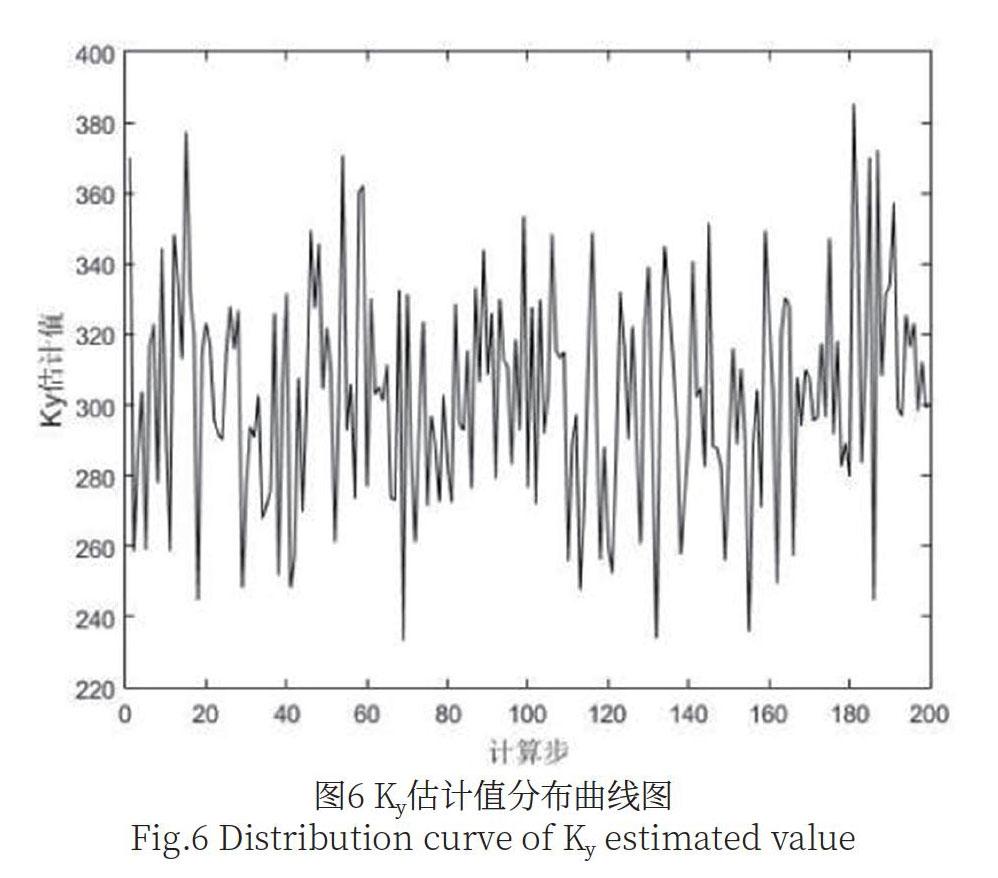
当弹簧处于轻微故障时,此时相关的性能参数就会衰减0%~25%,因此我们设置弹簧刚度的参数性能衰退20%,当弹簧处于轻微故障时,弹簧刚度参数的估计值分布曲线如图6所示:
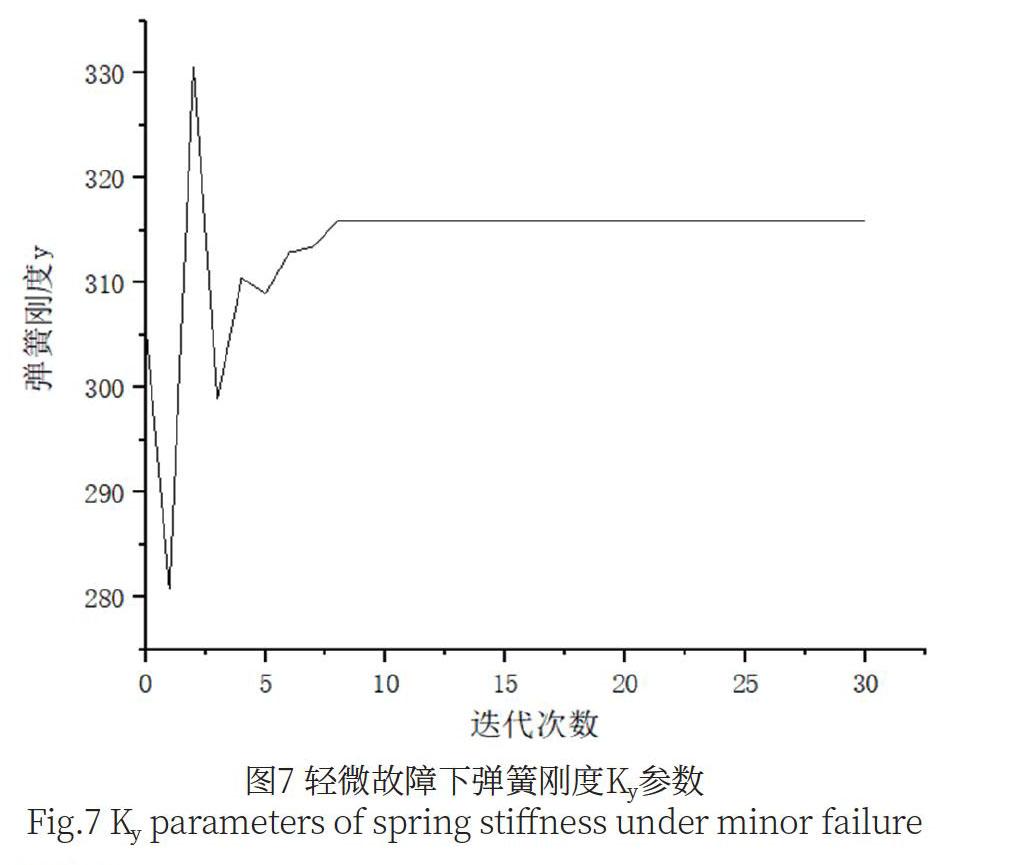
利用蚁群算法对关键部件参数进行估计。在轨道车辆转向架弹簧在轻微故障下运行时,利用蚁群算法对弹簧刚度进行寻优计算后,其横向悬挂弹簧刚度Ky的参数值为315.93MN/m,如图7所示。
4结论
本文通过建立的参数估计模型,引入蚁群算法对轨道车辆走行部关键部件弹簧在正常状态、轻微故障两种不同状态下,对弹簧的状态参数进行估计,结果表明:该方法对算法的初始值的要求不高,但是由于全局搜索能力强、收敛性好,对轨道车辆走行部关键部件弹簧的实际参数值能够进行有效估计,并且精度较高。
参考文献
[1] 漆瑾.高速机车走行部实时在线监测与诊断方法的研究[D].成都:西南交通大学,2006.
[2] LI P,GOODALL R,WESTON P.Estimation of Railway Vehicle Suspension Parameters for Condition Monitoring[J].Control Engineering Practice,2007,15(1): 43-55.
[3] 杨凯.车轮踏面擦伤检测系统研究[D].成都:西南交通大学,2005.
[4] 王福天.车辆系统动力学[M].北京:中国铁道出版社,1994.
[5] 方宇,陈龙,李晓斌,等.基于再次均匀采样策略改进轨道车辆二系悬挂系统参数估计方法[J].中国铁道科学,2013,34(3):72-78.
[6] 谢克明.现代控制理论[M].北京:清华大学出版社,2007.
[7] 李朝辉.连续域蚁群算法的改进研究及在参数估计中的应用[D].长沙:中南大学,2011.
