船体结构冰载荷的远场识别方法及试验验证

孔 帅，陈晓东，崔洪宇，季顺迎

（1.中国船舶科学研究中心，江苏无锡 214082；2.大连理工大学工业装备结构分析国家重点实验室，辽宁大连 116024）

0 引 言

全球气候变暖导致北极海冰加速融化，连接欧亚大陆的北极航道从最初的尝试性通航变成了现今的运营常态化、商业化[1]。冰区船舶作为航运重要载体，其结构安全性不容忽视，不仅需要严格按照规范设计建造和定期检修，更需要冰载荷监测系统以实时评估冰载荷是否会对结构造成损伤或永久性损坏[2-3]。基于船体艏部、舯部及螺旋桨冰激响应应变的冰载荷识别技术是目前主流技术手段[4-8]。而实际测量中船体结构往往会因防水舱、线缆舱等密闭结构导致需要监测区域的空间狭小、不宜布置传感器。工程中可采用远场监测技术解决不可接近、载荷场易受传感器干扰和传感器不便安装的载荷识别问题[9-11]。

冰区航行船舶外板结构的冰载荷识别通常基于影响系数矩阵法，其影响系数矩阵是在静力分析基础上通过依次对测量子区域施加单位载荷得到[4-6]。影响系数矩阵法采用直接求逆办法识别冰载荷，而影响系数矩阵可能会因自身的病态性和测量信号的噪声而导致解与真实载荷之间存在较大的偏差。为防止载荷反演过程中出现解不稳定的问题，需要向原始载荷识别模型中引入附加条件而使之变为可稳定求解系统的正则化方法[12]。根据求解目的和精度要求，已发展出众多的正则化技术，如通过引入滤子函数的截断奇异值分解法[13]和Tikhonov 法[12]，对工程中的不适定问题具有较好的效果[7,14-15]。但当求解矩阵规模较大或极度病态时，则需采用正则化能力更强的迭代式算法，如采用新型分数阶迭代型Tikhonov算法可以很好识别旋转结构所受的载荷[16]，采用Gram-Schmid正交化预处理的最小二乘QR 分解方法对桥梁上移动载荷识别精度很高[17]。适用于求解大维数、非对称和非正定方程的共轭梯度最小二乘算法(Conjugate Gradient Least Squares)是一种高效的迭代式算法[18]，可很好地识别壳结构和锯齿结构所受的环境载荷[19-20]。动载荷识别算法是基于递推连锁计算格式的，其初值敏感性和误差累积等特性极易受噪声信号影响[21]，故合理有效的滤波器可有效降低噪声的影响[22]。

为实现对船体外板结构冰载荷的远场监测，本文将构建一种基于Green 核函数、共轭梯度最小二乘迭代式正则化算子和移动平均滤波技术的冰载荷识别模型，并采用数值仿真和船体外板载荷识别试验对该模型进行评估。

1 船体结构冰载荷远场识别中的载荷反演问题

现有船体结构冰载荷监测系统中的影响系数矩阵法尚不具备解决远场监测的能力，因而，适宜的反演理论和正则化方法是实现船体结构冰载荷远场监测和提升反演精度的关键途径。

1.1 冰载荷远场监测中典型破冰船外板结构模型

各国的破冰船外板结构因依据不同的冰级规范而有差别，本文建立的典型破冰船外板结构模型主要参考中国极地科考破冰船“雪龙2 号”外板结构形式和其他学者关于典型破冰船外板冰载荷承载力研究工作[23]，该外板结构由船舶肋骨、强肋骨、纵桁和外板组成，其具体尺寸信息标记于图1中。在冰载荷反演过程中，船体结构假设处于线弹性阶段[3-6,24]。结构阻尼选择为比例阻尼。弹性模量为206 GPa，泊松比为0.3，结构钢材密度为7 850 kg/m3。边界条件参考ABS 冰级船规范标准，在模型上下平面内的边设置为在x方向自由，左右平面内的边设置为关于yoz面对称[23]。图中方框区域为不便安装测试设备但需重点监测的区域，监测区域大小为3 m×2.8 m。远场测量的位置选择在距离监测区域1.2 m 的肋骨上，并选择船体的冰激应变作为测量的响应信号。

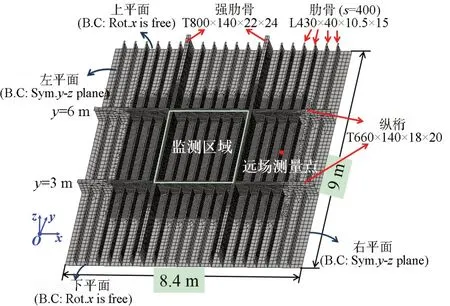
图1 典型破冰船外板结构有限元模型Fig.1 FE model of the typical shell structure of an ice breaker

1.2 利用Green核函数建立冲击载荷与应变间的响应关系

对于任意t时刻作用在船舶结构上单位冲击载荷可用狄拉克函数来定义，其函数如图2（a）所示;在监测区域施加单位载荷后，其监测点对应应变的核函数响应如图2（b）所示。

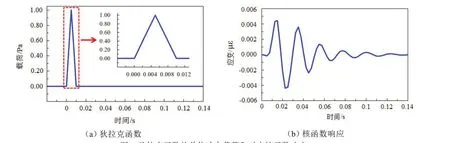
图2 狄拉克函数的单位冲击载荷和对应核函数响应Fig.2 Unit impact load of Dirac function and the corresponding kernel response

根据线性时不变系统的叠加原理可知，系统的响应可表示成单位脉冲载荷与冲击载荷的卷积，由此建立监测点冲击载荷与远场测量点应变间的响应关系，即式中，gi为ti=i·Δt时刻的Green函数。

由此建立基于Green 核函数的冰载荷远场监测反演的正问题，由gi分别组成冰载荷反演的Green核矩阵G，即

式中，ε、p分别为应变信号和施加的冲击载荷。

实船冰载荷识别中，根据已经建立的核矩阵G和测量的应变信号ε进行求解获得冰载荷时程p。

1.3 冰载荷远场识别系统不适定性的分析

采用Green 核函数的动载荷识别问题，其核矩阵G通常是病态的，这里从矩阵G极大的条件数可知，矩阵G几乎是奇异的。

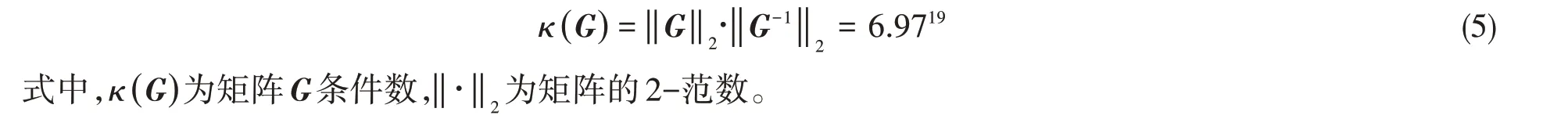
矩阵本身病态性是衡量系统求解稳定性的一个指标，同时测量中混入噪声的应变(即εerr)影响也不容忽视。根据奇异值分解定理，式（4）的解可表示为

式中，σi为Green 核函数矩阵G的奇异值，ui和vi分别为矩阵G的左右奇异向量，εerr,ui表示εerr和ui的内积，即广义傅里叶系数。

分析式（6）可知，冰载荷识别系统解的稳定性主要由Green 矩阵的小奇异值和测试信号噪声水平两个因素决定。式（6）可采用直接求逆办法求解的充要条件是系统应满足Picard 条件，即广义傅里叶系数的下降速度要比奇异值的下降速度快[25]。

由此可知，可采用Picard 曲线对求解系统的病态程度进行量化分析。图3（a）为没有噪声信号时的Picard 曲线，可看出此时广义傅里叶系数的下降速度并不比奇异值下降速度快，二者之间的比值呈现出稳定上升的趋势。图3（b）是噪声水平为5%时的Picard曲线，可以看出此时广义傅里叶系数的下降速度已远远小于奇异值的下降速度，该系统处于严重病态程度。因而，船体结构远场载荷识别中不管是否有噪声信号干扰，采用直接求逆的办法都不可行，必须采用正则化方法控制解的误差。

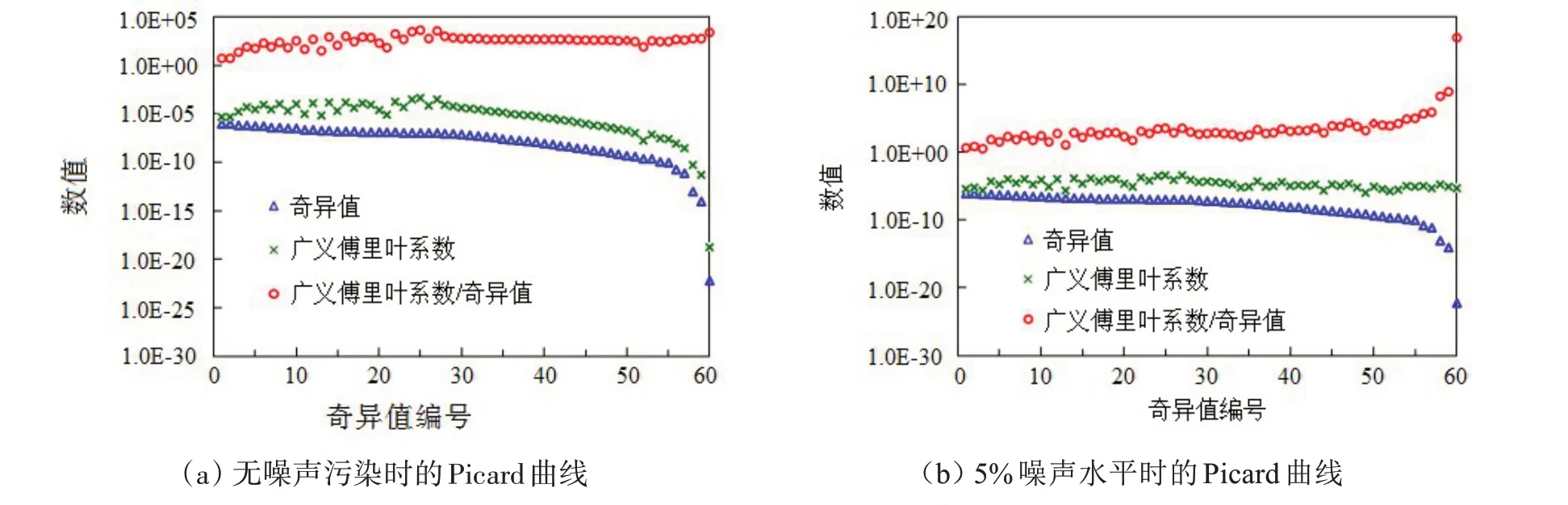
图3 两种噪声水平下的Picard曲线Fig.3 Picard curves under two noise levels

2 共轭梯度最小二乘正则化算法与移动平均滤波

采用共轭梯度最小二乘正则化算法可较好地解决非线性和非正定矩阵的求解问题，其迭代算法在识别精度和抗噪性等方面优势明显[19]。为进一步提升识别模型抗噪性，本文引入应用较多且滤波效果明显的移动平均滤波技术[22]。

2.1 共轭梯度最小二乘迭代算法及其终止迭代法则

载荷反演中提高求解精度的问题属于数学优化中的最小二乘问题，采用求解技术使反演的解与真实解之间误差的平方和最小

式中，pk为采用共轭梯度最小二乘算法经过k次迭代后的解。

共轭梯度算法首先要对矩阵G进行正规化处理和相关计算量的初始化：

式中，p1为共轭梯度算法的初始解，r1=εerr为解的残差的初始值，q1为共轭迭代过程中间量的初始值。

当k＞1 时，共轭梯度最小二乘迭代算法过程为

式中，αk、βk、qk为共轭迭代过程中间量，rk为迭代k次之后解的残差。

因共轭梯度算法为半收敛算法，合理的迭代终止法则有助减少算法的“过拟合”和“欠拟合”问题。本文采用Paige等[26]和Chang等[27]针对最小二乘问题提出的终止迭代法则

式中，γ为小于1的正数。

2.2 移动平均滤波

船体冰激应变信号经传感器转换和桥路放大器处理后不可避免地要混入干扰的噪声信号，同时因外板结构刚度较大和监测距离较远，会导致信号的幅值较小，因而采集得到的应变信号噪声水平会很高。为进一步降低信号噪声对反演结果精度的影响，本文采用移动平均的滤波技术进行信号处理。移动平均滤波器可以对输入信号进行平滑，起到低通滤波的效果，

式中，εˉ(t)为经移动平均滤波器处理后的应变信号，ε(t)为原应变信号，Ta为移动平均时间。

至此，建立了基于Green 核函数、共轭梯度最小二乘法和移动平均滤波技术的船体结构冰载荷远场监测模型，可采用数值仿真和结构试验对模型的识别效果进行评估。

3 冰载荷远场识别模型的数值分析和试验验证

冰区航行时，船舶肋骨作为结构主要承力构件而易发生结构破损[28-29]，实船冰载荷监测系统的应变传感器通常会布置在船舶肋骨上[5-6，24]。因而，可通过外板结构冰载荷识别数值仿真技术和外板载荷识别试验评估在船舶肋骨上进行远场监测的可能性和准确性。

3.1 典型外板结构冰载荷远场识别的数值分析

船-冰作用中的冰载荷呈现出三角波的函数形式，因而可在数值仿真中采用三角波模拟海冰载荷时程[6，28]。在图1中的监测区域施加如图4中实线所示的冰载荷时程，因实船测量中冰载荷具有很强的随机性[30]，其施加载荷时程的峰值和周期也设置成不同的。采用冰载荷远场识别模型对其冰载荷进行识别，从图4 的时程曲线对比可知共轭梯度最小二乘迭代算法反演的载荷时程能准确地对应上冲击载荷的信号时程，但采用直接求逆反演的载荷时程已严重偏离施加载荷的时程。

图4 远场冰载荷时程曲线及反演结果Fig.4 History curve of ice loads in the far-field and identification results

为评估该数值模型的反演效果，本文引入相对误差和相关性系数评估反演结果和真实施加载荷之间的拟合精度和相关性，其定义为

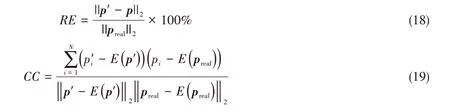
式中，RE和CC分别为相对误差和相关性系数，p'和preal分别为反演结果和真实施加载荷列向量，p'i和pi分别为第i个时间点时的反演载荷和真实施加载荷，E(·)表示列向量均值。

在实际结构测量中，带噪声应变信号εerr可写作

式中，εerr为含有噪声信号的应变信号，lnoise为百分数，std(ε)为ε标准差，代表噪声的水平，rand(-1,1)为(-1,1)之间的随机数。

为评估远场冰载荷识别模型的正则化能力及抗噪能力，直接将式（20）中定义的噪声信号施加到船体冰激应变中，噪声水平由1%增加到20%，增加步长为1%，图5为不同噪声水平下未经滤波处理和经过滤波处理识别结果的相对误差和相关性系数。分析可知，即使在20%噪声水平影响下，未经滤波处理的识别结果的相对误差也能维持在10%以内；相关性系数越接近1 说明信号之间的整体相关性越强，模拟中的相关性系数一直维持在0.99 以上说明其反演载荷可始终对应上施加载荷，未出现较大偏差。另外，经滤波处理后的结果相对误差明显降低、反演结果的相关性系数明显升高，说明其滤波器的降噪效果明显。因此，该模型中的正则化算子和滤波器可很好地控制反演矩阵中小奇异值和噪声信号的影响。

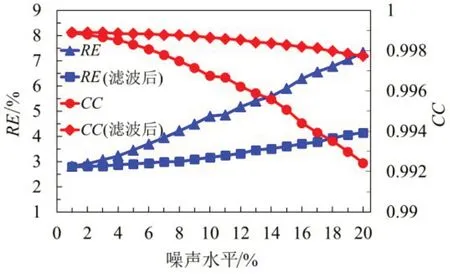
图5 不同噪声信号水平下相对误差与相关性系数Fig.5 Relative errors and correlation coefficients at different noise levels

3.2 船体远场冰载荷识别模型的试验验证

为评估识别模型在实际应用中的适用性和准确性，船体外板载荷远场识别试验在结构试验台上进行。图6（a）为载荷监测点与远场测量点在外板结构上的分布示意图，通过记录远场测量点的应变信号和载荷识别模型对监测点载荷时程进行识别。图6（b）为试验设备的整体视图，试验设备由施加载荷装置、外板结构和数据采集器三部分组成。船体外板结构由外板、肋骨和纵桁等强框架组成，如图6（c）所示。

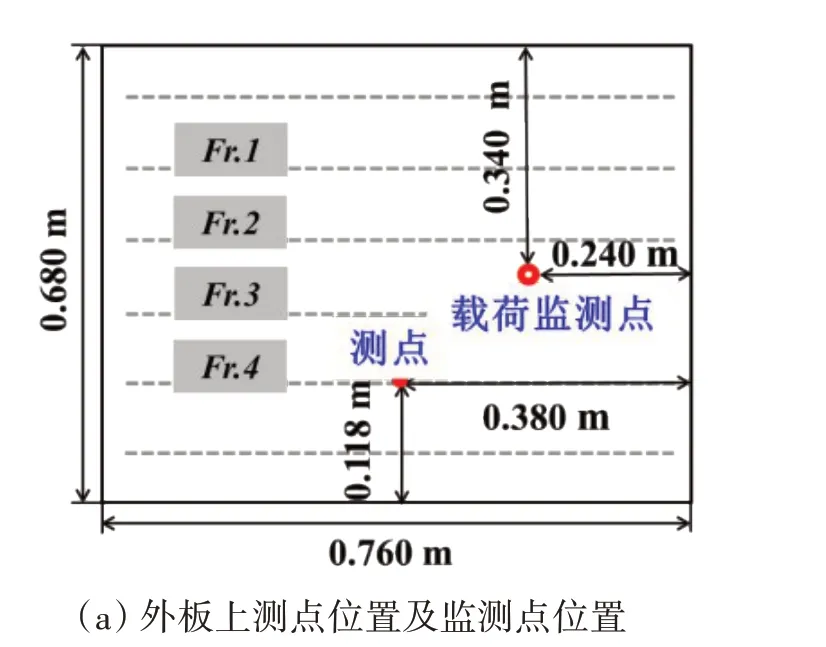
图6 船体外板远场载荷识别试验Fig.6 Far-field load identification test of the ship shell structure

为保证肋骨与真实结构之间的结构相似性最大化[28]，肋骨纵向端部与纵绗相固定，且监测及测量的位置均远离边界。试验模型中的板都采用3 mm 厚的铝合金板，弹性模量、材料密度和泊松比分别为70 GPa、2700 kg/m3和0.3。各国学者把船舶外板结构冰载荷识别中的边界条件通常设置为固支或接近固支[4-5]，故本文试验模型边界采用螺栓和边条的组合方式进行约束，同时数值模型中的边界条件也设为固支。在通过装置施加载荷的过程中，船舶外板结构并未出现影响到载荷识别精度的冰激振动现象。模型处于线弹性状态，结构阻尼采用比例阻尼。应变信号由DH5922N 进行采集，采样频率为10 kHz，数据采集过程中采用抗混滤波器。应变片采用带温度补偿片的半桥连接方式，同时采用靠近肋骨边缘且其方向平行于外板的贴片方式。本文采用速比为36∶1、螺距为6 mm的减速型丝杠升降机装置施加载荷，通过手摇方式控制丝杠升降（图6（b）所示的手摇装置），丝杠升降过程中对试样加载力由图6（b）所示的压力传感器直接测量得到。

采用加载设备对载荷图6（c）中的监测点施加两次载荷时程，加载的时程曲线如图7（a）和图7（b）所示，加载的时程曲线也呈现三角波的形式。对应的应变时程曲线如图7（c）和图7（d）中的细实线所示，可看出两次加载工况应变信号的噪声水平在整个时程都高于40%。采用移动平均滤波后的应变时程如图7（c）和图7（d）中的的粗实线所示，其信号可以较为准确地描述原信号的时程特征。实船测量中的冰载荷与肋骨上应变间的关系是无法校验的，仅能通过加载装置进行验证。对比Ricth等[4]和Suominen 等[5]的冰区船舶加载试验可知，本文测量得到的应变-加载力之间的对应性与其是一致的。

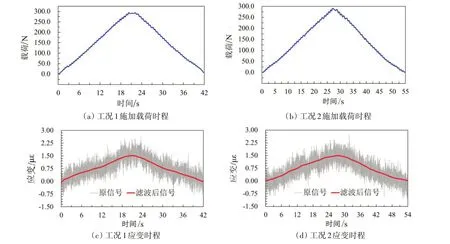
图7 原应变信号及经移动平均滤波器处理后的信号Fig.7 Original strain signals and the signals processed by the moving average filter

反演的载荷时程如图8中的方形点所示，载荷信号整体上呈现出三角波的形式，反演信号的采样频率为2 Hz。施加的载荷信号如图8 中实线所示。对比二者信号时程可知，整个时程均可以很好地对应施加载荷的时程曲线。两个工况下识别的相对误差分别为5.73%和12.59%，相关性系数分别为0.997和0.996。识别载荷误差主要来自于真实结构与数值模型之间不可避免的误差和应变信号较大的噪声水平。

图8 施加载荷时程及反演载荷时程Fig.8 Time history curves of the applied loads and the identified loads

4 结 语

实船的冰载荷监测是保障冰区航行船舶结构安全、认知不同航行模式及不同冰型下冰载荷特征的重要途径。本文提出的船舶结构冰载荷远场识别模型是对原有冰载荷监测方案的扩展，可提升船体结构冰载荷监测范围，从而提升对船舶全船尺度下冰载荷分布的认知水平。通过对冰载荷远场问题适定性分析可知，其系统已达到不能直接求解的极度病态程度。对比直接求逆的办法可知，引入的共轭梯度最小二乘算法和对应迭代终止准则的正则化算子可很好地提升模型的载荷识别能力。结合正则化方法及移动平均滤波技术的识别模型识别了试验中两个工况的施加载荷，其时程特征都能较为准确地对应，也验证了该方法在工程中应用的可行性。为提高识别模型的反演精度及计算效率，下一步将从设计滤波器和迭代终止判断等方面出发对真实冰载荷进行识别分析，从而将其扩展到实船的冰载荷监测中。