四元域上多项式乘法Toom-3算法及其在量子密钥分发中的应用

黄观金,周华旭,陈创波,高鹏,凌杰

(1南方电网调峰调频发电有限公司信息通信分公司,广东 广州 510700;2安徽问天量子科技股份有限公司,安徽 芜湖 210042)

0 引言

1984年,IBM信息物理学家Bennett与加拿大蒙特利尔大学教授Brassard提出历史上第一个量子密钥分发(QKD)协议,简称BB84协议。此后,无论是理论与安全性证明,还是试验与应用均取得了长足的进展。其中,我国在QKD领域一直走在世界的前列。2009年,郭光灿小组建成了世界上首个量子政务网-芜湖“量子政务网”,在量子密码的实用化道路上建立了第一个里程碑,标志着我国量子保密通信技术已具备应用水平。2016年8月,我国成功发射全球首颗量子通信科学实验卫星“墨子号”。“墨子号”卫星在世界上首次实现了1200 km低轨卫星和地面站间量子密钥分发,突破了传输距离的极限,并在星地之间1400 km链路完成单光子量子比特隐形传态,为超远距离量子通信组网奠定了基础。

QKD采用两组非正交量子态作为信息载体,在通信双方实现对称密钥分发,其安全性由量子不可分割、测不准原理、未知量子态不可精确测量等量子力学原理保证,具有信息论可证明安全性。再结合一次一密方案可以实现无条件安全的保密通信。QKD分发主要包含以下几个阶段:量子信号制备、传输与测量、对基、纠错和安全增强等。在安全增强中需要使用通用哈希函数对密钥进行压缩,提取出安全密钥,其具体实现包括基于模算术、基于二元矩阵乘法和基于有限域乘法的安全增强方法,主要的计算复杂度分别在于大整数乘法、二元矩阵乘法和有限域上多项式乘法。QKD的安全性分析一般要求数据量至少要达到105～106量级,因此安全增强的效率特别依赖于实现这几类乘法的算法选择及其复杂度。

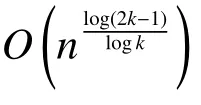
QKD中安全增强均基于二元域,且长度超过105。在数据量大时,会考虑用并行计算或硬件实现来提升性能,Karatsuba算法速度偏慢,Schonhage-Strassen/FFT虽然速度快但是需要消耗大量资源,Toom-3比较适中。但是二元域上多项式乘法Toom-3算法直到2007年才由Bodrato[4]给出,该算法需要额外执行小多项式的乘法和除法,其中除法并不适合并行计算与硬件实现。

本文提出一种四元域上多项式乘法Toom-3算法并给出详细的计算公式,进而提供了一种新的基于有限域乘法的安全增强方法,该方法适用于长度n=2m(其中m为奇数)的情形。所提出算法不需要额外进行小多项式除法,实际复杂度优于二元域上多项式乘法Toom-3算法,适合并行计算与硬件实现。

1 基于四元域上多项式乘法的安全增强方法

QKD在量子传输及纠错阶段均会泄露信息,安全增强使用通用哈希函数来压缩泄露的信息,并提取出安全密钥。假设安全增强前的密钥为n bit,QKD安全性分析根据合适的GLLP公式计算可提取的安全密钥量为k bit。记二元域F2=GF(2)={0,1},集合,其中k≤n为正整数。文献[5]提出使用通用哈希函数族来实现安全增强。通用哈希函数族的定义如下。

1.1 基于二元域上多项式乘法的安全增强实现方式

在上述安全增强过程中,最耗时间的是步骤4,需要进行二元域上多项式的乘法。二元域上多项式的乘法也有多种算法选择,例如引言中介绍的Karatsuba、Toom-3和Sch¨onhage-Strassen算法。其中文献[4]给出的Toom-3算法需要进行小多项式的乘法和除法,为改进安全增强的复杂度,下文提出一种基于四元域上多项式乘法的安全增强方法。

1.2 基于四元域上多项式乘法的安全增强实现方式

步骤5:对h进行投影,得到Projn,k(h)=(h0,h1,···,hk-1)∈F2k,即为安全增强的输出。

其中最耗时间的仍然是步骤4,需要进行四元域上多项式的乘法。四元域上多项式的乘法同样也有多种算法选择,如引言中介绍的Karatsuba、Toom-3和Sch¨onhage-Strassen算法。

2 四元域上多项式乘法Toom-3算法

Toom-3算法采用分治的思想将长多项式乘法分解为多个短多项式乘法,再递归循环将短多项式乘法分解为更短多项式乘法,最终获得性能上的优化。

四元域上多项式乘法Toom-3算法可分为5个步骤,具体计算与公式如下所述。

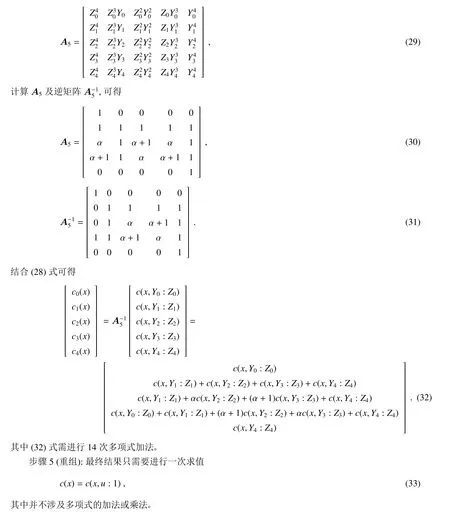
3 四元域上多项式乘法Toom-3算法复杂度分析

上一节四元域上多项式乘法Toom-3算法的复杂度分析如表1所示。在对多项式 f(x)∈F4[x]进行数量乘法αf(x)时,其复杂度等同于多项式的加法。另外,点P5的选取与矩阵计算等均是固定的,故不纳入计算复杂度中。

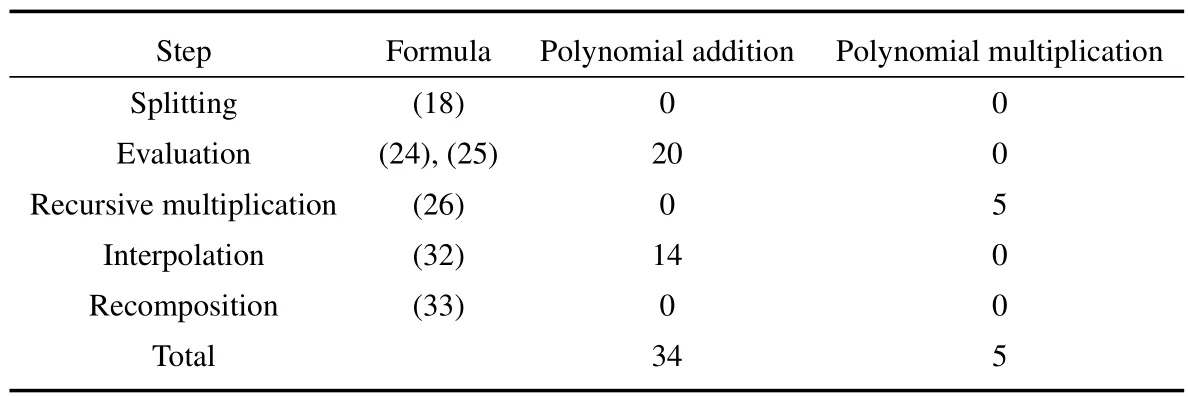
表1 四元域上多项式乘法Toom-3算法复杂度分析Table 1 Complexity analysis of Toom-3 algorithm for polynomial multiplication over finite field F4

4 总结与展望

提出一种四元域上多项式乘法Toom-3算法并给出详细的计算公式,并利用该算法实现基于有限域乘法的安全增强方法。与基于模算术或基于二元矩阵乘法的安全增强方法相比,所提出方法需求的随机数数量减半,算法复杂度达到了O(n1.465)。由于没有使用多项式除法,且Toom-3的算法本身采用分治思想,适合并行计算或硬件实现。目前QKD的密钥生成速度还无法真正保障一次一密对密钥量的需求,而安全增强速度的提升将为高速QKD的发展提供重要保障。

所提出方法的一个重要创新点在于通过考虑二元域的扩张,使得有限域上Toom-Cook系列算法成为可能。沿着相同的方向,可以考虑二元域的更高次扩张,实现更高次的Toom-k算法,也可以考虑其他非特征2有限域上的Toom-Cook系列算法,提供适合并行计算或硬件实现的更优QKD安全增强方法。