基于自适应门限的改进BigBand算法

庞 健 秦明伟 王 焕 姚远程

(西南科技大学信息工程学院，特殊环境机器人技术四川省重点实验室，四川绵阳 621000)

1 引 言

随着无线通信技术的迅猛发展，可供使用的频通信段越来越紧缺。同时，授权用户所分配的频段资源长时间空闲、非授权用户可使用的频段资源稀少。认知无线电技术(Cognitive Radio，CR)可通过高效地分配频段资源，提高频谱利用率，解决频谱资源匮乏问题。

频谱感知是实现认知无线电的基础和前提，尤其是GHz宽带频谱感知。根据奈奎斯特采样定理，采集高速率信号要求高采样率的模数转换器(Analog Digital Converter，ADC)。目前，由于高速、高性能的ADC工艺复杂、价格昂贵等原因，变得难以获取。

2006年，D.Donoho等人提出了采样率远低于采样定理的压缩感知技术(Compressive Sensing，CS)。其最大的特点是随机采样、边采样边压缩，能有效降低认知系统重建信号时所需的采样率，为认知无线电宽带频谱感知技术的实现提供了可行性方案。但在实际运用中，压缩感知也存在着计算复杂度高、硬件开销大、实时性难以保证等问题。

2014年，Hassanieh等人提出了BigBand欠采样算法。该算法的基本原理是利用信号时域时延与信号频域相位变化的关系，确定混叠频点的位置和幅值，最终从欠采样信号中恢复出宽带频谱。经理论验证，在理想条件下，利用两块42MHz和两块50MHz的ADC可以捕获1.05GHz的带宽。但算法中大量的参数来自经验数据(例如频谱混叠后的门限阈值)，在低信噪比和噪声剧烈变化的环境下，频谱感知性能较差。

基于以上问题，本文针对BigBand算法中的门限问题，通过对环境噪声和信号的统计分析，提出一种基于自适应门限的改进BigBand算法，该算法主要特点是将噪声门限、信号门限与预设信号虚警概率及感知环境的信噪比相关联，并参考历史判决结果选取门限值，以提高BigBand算法的抗干扰性和检测性能。

2 BigBand算法

BigBand算法的难点及重点在于解决频谱混叠问题，主要为混叠频点频率和幅度计算。

2.1 频点分桶

信号的频域可表示为

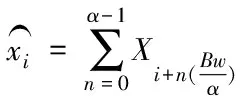
(1)

由式(1)可知，频点由间隔

α

均匀散列分布到同一个频率范围内(称之为桶)。频率

f

分布桶的位置为

i

=

f

(

Bw/S

),桶中的值是散列分布到桶中频点的值之和。

在大多数情况下，检测的频谱是稀疏的(频谱使用率在5%左右)，所以BigBand算法将桶的能量(即幅度平方)与接收器的噪声进行比较，将能量低于门限值的桶视为空桶并忽略，将焦点放在有信号的桶上。这样不仅能降低计算复杂度，还能提高频谱感知速度。

2.2 频率估计

若在同一个桶中只散列分布了一个大值频点(信号频点)，则认为不发生频谱冲突，此刻桶的频率值即为该单一大值频点的值，确定该大值频点频率值的过程称为频率估计。

在快速傅里叶变换(Fast Fourier Transformation,FFT)中，利用信号时域的偏移与频域的相位变化的关系，可以估计出频率

f

。

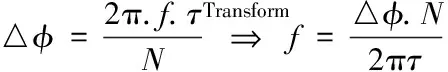
(2)

式中：

τ

——输入信号采样的时间偏移量。由于相位周期为2π，为了避免频率值较大时引起的相位环绕，

τ

的值必须非常小，理论上

τ

的阶数应为1

/Bw

。

2.3 频点冲突检测与处理2.3.1 频点冲突检测

若在同一桶中散列分布了两个或两个以上的大值频点，则认为发生了频谱冲突。冲突检测的方法利用FFT的相位旋转特性，具体如下。

未发生冲突时，即桶中只有一个大值频点，若延时前后该桶中频点的值分别用

X

′(

k

)，

X

′()(

k

)表示，则它们的关系可表示为

X

'()(

k

)=

X

′(

k

)

.e

2π=

X

(

f

)

.e

2π

(3)

在延时前后，频率值会随延时

τ

的改变而改变，但幅值是不变的，均为

X

(

f

)。当大值频点

f

和

f

′发生冲突时，延时前桶中的频点的值

X

′(

k

)为

X

′(

k

)=

X

(

f

)+

X

(

f

')

(4)

延时后该值为

X

'()(

k

)=

X

(

f

)

.e

2π+

X

(

f

′)

.e

2π

(5)

通过比较

X

′(

k

)和

X

′()(

k

)的幅度值是否相等，即可以检测出信号欠采样后是否发生了冲突。

2.3.2

频点冲突处理

互质采样(根据中国剩余定理)保证了两个频率在一次采样中发生碰撞，在另一次采样中不会发生碰撞。通过迭代的方法来解决冲突，即混叠频点的值减去非混叠频点的值得到混叠前两个频点的频率值。

捕获频谱带宽

Bw

，需要使用到两个ADC，它们的采样速率分别为

Bw/α

、

Bw/β

，

α

和

β

和互质。在前述还有一个延时

τ

的采样，因此BigBand算法分别需要两种不同采样率的低速ADC两个，具体算法流程如图1所示。

图1 BigBand算法流程图Fig.1 Flow chart of BigBand algorithm

3 自适应门限算法

3.1 门限问题分析

在传统BigBand算法中，对桶的门限设定主要依靠经验，将高于某一门限值的桶判定为信号桶，其余的桶设定为零。理想情况下，信号值相对于噪声值是一个相对大值，设置一个较高的门限就可以将噪声桶全部去掉，保留全部信号桶，最后通过解频谱混叠恢复出原始宽带频谱。

在实际情况中，因为环境中存在噪声干扰，每一个桶都是有值的，频谱混叠会使噪声的值被叠加放大。在复杂的环境下，信号淹没在噪声中，信号桶与噪声桶更是难以区分，一个合理的桶门限阈值至关重要，这个阈值既要能保证所有的信号桶被保留，又要尽可能多的去除噪声桶。由经验获得的门限阈值不适用于这种复杂环境。

3.2 门限算法

针对噪声不确定性及低信噪比的复杂环境，本文提出基于自适应门限的改进BigBand算法，该算法利用复杂环境的信噪比差异，动态调整桶的门限阈值，使判决门限与信噪比相关联，提高BigBand算法在复杂噪声环境下频谱感知的准确性。

首先，由预设虚警概率获得初始噪声桶阈值

λ

和信号桶阈值

λ

，再感知不同信道得到信道信噪比。然后根据信噪比获得两个桶阈值的加权因子，并通过加权因子调整门限阈值，最后根据历史数据选择新阈值作为门限进行判决与感知。根据信号虚警概率

P

可获得初始噪声桶门限

λ

和信号桶门限

λ

可表示为

(6)

(7)

判决门限的加权因子可表示为

(8)

式中：

T

——门限计算时的加权因子；

SNR

——频谱感知信道的信噪比；

N

——需要进行门限判决的被检测桶的数目。

依据加权因子对获得的初始门限阈值进行调整的计算公式为

λ

_

T

1=

λ

/T

(9)

λ

_

T

2=

λ

/T

(10)

考虑感知信道的历史使用情况，选择判决门限。若前一时刻检测到信号值即主用户存在(H)，则选择

λ

_

T

1作为当前检测的门限值；若前一时刻主用户不存在(H)，则选择

λ

_

T

2作为当前的门限值。门限判决方法流程如图2所示。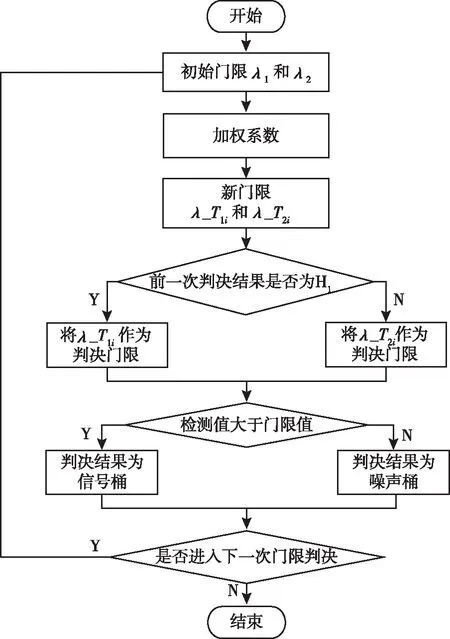

图2 门限判决方法流程图Fig.2 Flow chart of threshold judgment method

4 实验结果与分析

在信噪比为-17dB条件下，基于自适应门限的改进BigBand算法得到的桶门限，如图3所示。噪声桶门限可以滤去大部分的噪声桶，但还是会有部分少量噪声桶信号大于噪声门限，此时信号桶门限就可以发挥只保留信号桶作用。

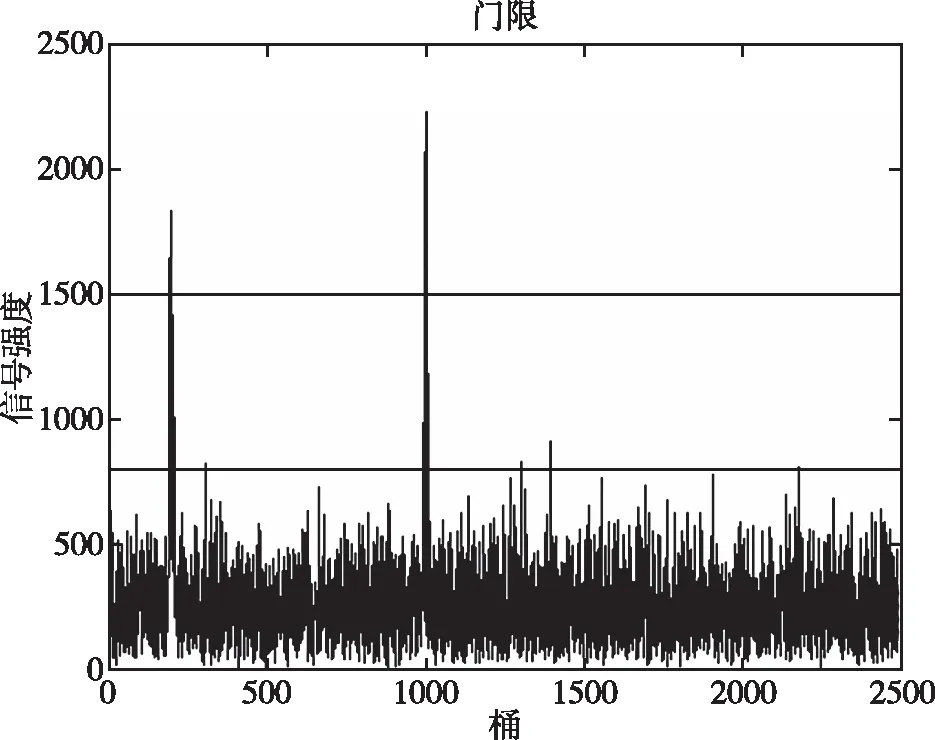
图3 SNR=-17dB时得到的门限域值波形图Fig.3 Wave of threshold value obtained when SNR=-17dB

为了进一步证明改进BigBand算法的有效性和感知的准确性，在matlab上对算法进行了验证。在信号不同的虚警概率条件下，测试改进BigBand算法与传统BigBand算法的检测性能，同时与经典的能量检测性能进行比较；并在不同信噪比条件下测试改进BigBand算法的频谱感知性能。

在信噪比为-17dB条件下，改进BigBand算法、BigBand传统算法和传统的能量检测算法的信号检测概率与信号虚警概率变化关系，如图4所示。从结果中可得，在固定信号虚警概率的条件下，改进BigBand算法的检测概率明显高于其他两种检测算法，频谱感知的准确性更好。在信号检测概率接近1时，改进算法的信号虚警概率明显低于传统BigBand算法。

图4 不同检测算法性能对比曲线图Fig.4 Comparison of detection performance based on different detection algorithms

在不同信噪比条件下，改进BigBand算法的信号检测概率与信号虚警概率变化关系，如图5所示。从仿真结果中可得，在信噪比条件一定时，检测性能随信号虚警概率的增加而变得更好。在信号虚警概率一定时，信噪比越高，信号检测性能越好即频谱感知准确性更好。同时，可以注意到，在不同信噪比条件下，信号的检测概率是趋于一致的，且变化范围较为接近。可以说明改进BigBand算法可以适应一定复杂程度的噪声环境。

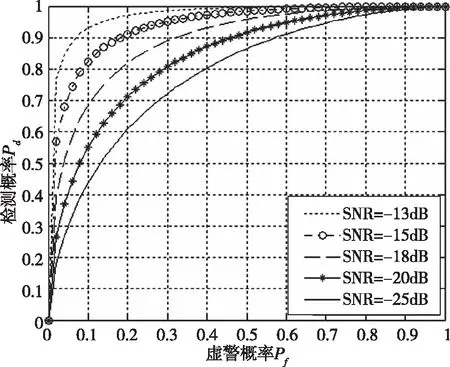
图5 不同信噪比环境下检测性能曲线图Fig.5 Detection performance curve under different SNR environments

5 结束语

本文针对BigBand算法在复杂噪声环境中感知性能较差的问题，对BigBand算法进行改进。在其依靠经验获取判决门限的基础上，利用预设信号虚警概率作为条件获得初始门限阈值，再通过感知信道的信噪比调整门限阈值，并参考信道的历史感知结果选择判决门限。MATLAB仿真结果表明，该算法的检测性能优于传统的BigBand算法，在低信噪比及噪声变化剧烈的环境下能考虑到环境噪声对检测性能的影响，具有较好的噪声环境适应性和抗干扰性。能进一步提高BigBand算法频谱感知的可靠性和准确性。