在轨质量测量仪地面校准技术研究
2021-08-17彭建国
廖 航 彭建国 周 鑫
(四川航天计量测试研究所,四川成都 610000)
1 引 言
在国家建设航天强国的战略思想指导下,中国航天事业正有序加速推进,已具备长期飞行、进行空间科学实验的技术条件。
在轨质量测量仪作为货运保障分系统重要便携手持设备,主要用于在轨微重力环境下的货包质量测量,在货运飞船撤离空间站时,为货舱内货物配平提供数据。为确保在轨质量测量仪在轨测量精度,上行前需进行地面校准。由于空间无重力场环境,无法使用常规校准方法和设备获取质量,测量不确定度不适用于实际情况,因此需要根据在轨质量测量仪设计原理、使用环境及测量对象,开展地面校准方法研究。
2 在轨质量测量仪地面校准方法
2.1 在轨测量原理及使用方法
微重力环境下物体质量测量面临以下问题。
1)常规地面测量方法均基于稳定重力场环境,而空间无重力场环境;
2)微重力环境下物体质量测量方法及校准技术存在能力短板;
3)基于在轨实际使用需求,测量设备需满足高精度、低功耗、轻量化的工程要求。
为解决上述问题,可使被测物体运动,通过测量与物体质量相关的物理量推算出物体质量。目前,国内外在轨实现质量测量的主流研究和使用方法有:利用振动原理、动量定理、牛顿第二定律和离心力原理四大类。
2.1.1
振动原理根据质量-弹簧系统自由振动的周期与总质量,满足式(1)可以计算出被测物体质量。目前通过飞行验证的质量测量设备有IM(俄)、BMMD(美)、SMMI(美)、SLAMMD(俄)。
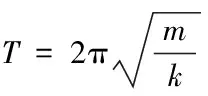
(1)
式中:T
——被测物体振动周期;k
——弹簧或杆等弹性元部件的回复力系数。2.1.2
动量定理利用标准质量物体与被测物体发生碰撞,通过测量两者发生碰撞前后的速度变化量,根据动量守恒定律如式(2),可计算出被测物体的质量,适用于刚性体物体质量测量
mΔν
=m
Δν
(2)
式中:m
——被测质量;Δν
——碰撞前后的速度变化量;m
——标准质量。或使被测物体碰撞力传感器,测量撞击过程中的作用力以及碰撞前后的速度变化,根据式(3)动量定理推算出质量
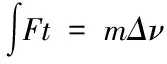
(3)
式中:F
——撞击过程中的力传感器作用力;Δν
——碰撞前后的速度变化。2.1.3
牛顿第二定律对被测物体施加外力使其做直线加速度运动(可通过对被测物体施加恒定外力实现直线加速运动,也可通过将被测物体安装在特定的运动机构上直接控制其进行直线加速运动),根据牛顿第二定律如式(4),在已知外力和加速度条件下,直接计算出被测物体的质量。
F
=ma
(4)
式中:F
——对物体施加的作用力;a
——加速度。2.1.4
离心力原理利用被测物体做标准圆周运动,其质量、离心力、质心旋转半径、旋转角速度满足离心力如式(3),利用外部测量工具获取各值,即可计算出被测物体质量为
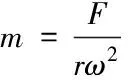
(5)
式中:F
——离心力;r
——质心旋转半径;ω
——旋转角速度。针对上述4种测量方式,对其测量实用性、被测对象要求、测量精度、系统复杂度及在轨实现难度分析见表1。
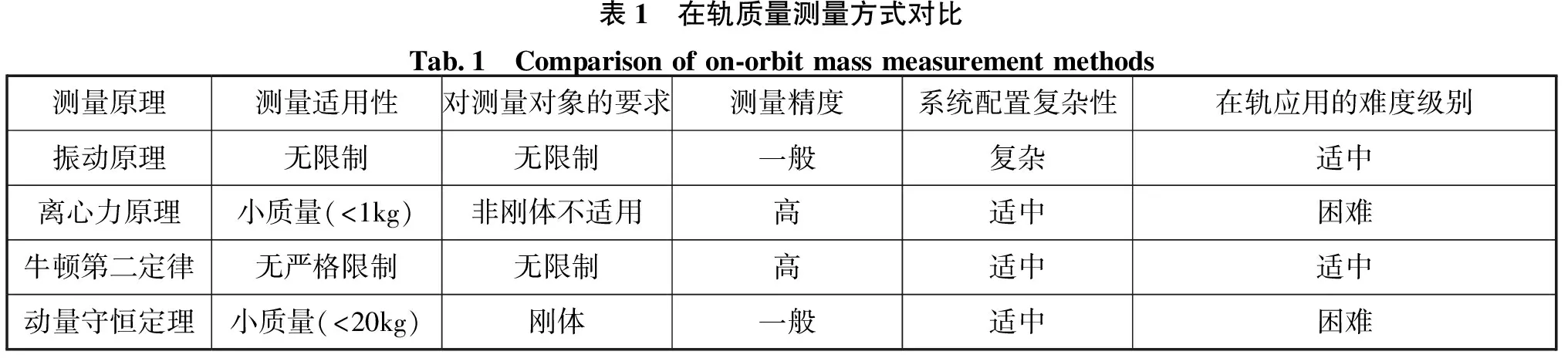
表1 在轨质量测量方式对比Tab.1 Comparison of on-orbit mass measurement methods测量原理测量适用性对测量对象的要求测量精度系统配置复杂性在轨应用的难度级别振动原理无限制无限制一般复杂适中离心力原理小质量(<1kg)非刚体不适用高适中困难牛顿第二定律无严格限制无限制高适中适中动量守恒定理小质量(<20kg)刚体一般适中困难
从表1可以看出,利用牛顿第二定律进行质量测量的设备精度高,系统实现难度小,综合性能最好。在轨质量测量仪实际测量货包时,宇航员和货包处在漂浮状态,自身姿态控制困难,动作迟缓费力,货包不能移动较大的距离和具有较高的运动速度,因此在轨质量测量仪采用小行程牛顿第二定律过程测量技术,根据在轨测量和操作要求,通过对捆扎后的货包施加快速拉动的作用力,使货包产生相应的加速度,计算得到货包的质量,测量原理如图1所示。

图1 在轨质量测量仪操作原理图Fig.1 Operation principle diagram of on-orbit mass measuring instrument
2.2 地面校准方法
地面校准方法按照“校准的过程应尽可能与在轨使用状态一致”的原则,需对在轨测量环境、被测对象以及测量方法进行深入研究分析,突破地面微重力环境模拟、测量过程算法模型搭建等关键技术,缩小测量过程天地差异,以更小的误差和更高的精度实现在轨质量测量仪地面校准系统研制,同时开发校准过程监测软件,对测量过程有效性进行实时监测,解决专用测试设备的地面校准问题。
通过调研类似环境与原理性仿真分析,研制了与在轨状态一致的校准专用货包,通过高塔悬吊式将货包悬吊一定高度,模拟了水平二维微重力环境,缩小天地差异。通过施加水平拉力拉动货包,使其获得一定的加速度,根据牛顿第二定律,实现在轨质量测量仪地面校准,其原理如图2所示。

图2 地面校准原理图Fig.2 Principle of ground calibration
3 地面专用校准装置研制
根据前述地面校准方法,研制地面校准系统,缩小测量环境天地差异,保持测量环境一致性,确保在轨质量测量仪测量精度,实现在轨质量测量仪的地面校准。根据货包结构特点和装载要求及质量测量原理,采用高塔悬吊式试验装置模拟水平二维微重力环境,由钢丝绳悬吊机构、可调水平升降工作台、三轴加速度输出检测装置、指向重力方向的力检测装置、固定质量测量仪拖板、一系列具有标准质量的被测货包和计算机系统组成,如图3所示。
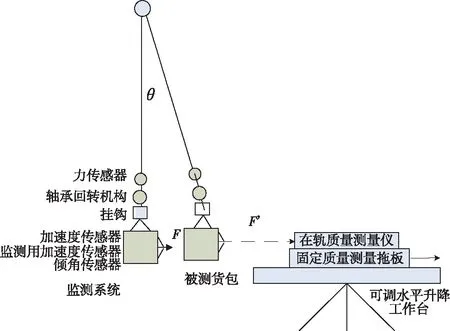
图3 地面校准装置示意图Fig.3 Ground calibration device schematic
3.1 校准专用货包研制
为尽可能与实际使用状态保持一致,按照在轨货包材料、外形、结构、力学特性和装载要求,设计了3种外形规格,研制不同的内衬赋型,达到均匀装载的要求,包体颜色均为本白色,并通过天平校准其质量,作为校准用的标准质量货包。
3.2 微重力环境模拟
测量仪在货运飞船微重力和正常大气压环境下使用,为实现上行前对其指标性能及测量精度进行验证,需在地面环境下模拟微重力环境。目前,根据国内外有关报道及相关资料显示,地面正常大气压环境下,模拟微重力环境主要方法有四类,见表2。
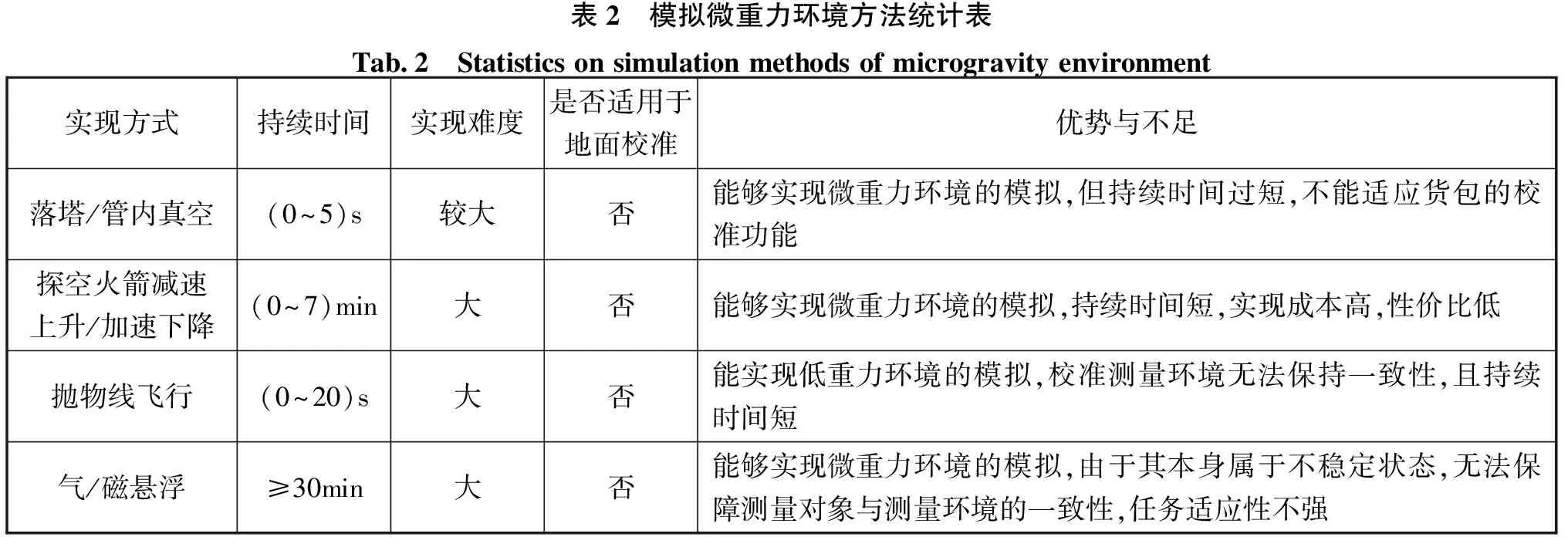
表2 模拟微重力环境方法统计表Tab.2 Statistics on simulation methods of microgravity environment实现方式持续时间实现难度是否适用于地面校准优势与不足落塔/管内真空(0~5)s较大否能够实现微重力环境的模拟,但持续时间过短,不能适应货包的校准功能探空火箭减速上升/加速下降(0~7)min大否能够实现微重力环境的模拟,持续时间短,实现成本高,性价比低抛物线飞行(0~20)s大否能实现低重力环境的模拟,校准测量环境无法保持一致性,且持续时间短气/磁悬浮≥30min大否能够实现微重力环境的模拟,由于其本身属于不稳定状态,无法保障测量对象与测量环境的一致性,任务适应性不强
由表2可知,上述模拟微重力环境的方法持续时间短、成本高、实现的漂浮状态不够稳定,均不适用于货包质量测量过程的校准需求,因此需要根据在轨质量测量仪实际操作使用工况和要求研究微重力环境模拟方法。
针对校准过程中货包结构、装载、质心位置、静稳定状态要求进行仿真分析和试验摸底,最终采用高塔悬吊的方式,用一定长度的悬吊绳将标准质量货包悬吊一定高度,使悬吊绳的拉力和货包的重力抵消,实现标准质量货包的水平二维平面漂浮,悬吊绳、挂钩和被测货包之间的连接关系如图4所示。
根据仿真试验结果,按25m的长度悬吊不同质量的货包选取不同直径的钢丝绳,在水平力拉动移动时,使货包的上升高度引起的加速度变化最小,同时确保钢丝绳的质量要小且柔韧。同时,为精确测量钢丝绳悬吊力的变化,按照不同的悬吊货包质量匹配不同量程的测力传感器。
3.3 可调水平工作台
由于前述微重力模拟环境是水平二维平面,测量货物时拉力也应水平,根据不同规格货物悬吊高度与姿态,设计可调水平升降工作台为测量仪提供水平运动支持条件,并为其设置固定拖板便于提供水平运动导向。校准时,为防止重力产生附加的加速度,通过调整水平升降工作台的水平倾角和工作台高度,为固定测量仪拖板的移动提供水平运动导向,使三根施力绳的合力轴线高度与在轨质量测量的测力传感器的位置处在同一高度,实现标准质量货包在水平二维面上运动。
3.4 监测系统
地面校准是建立在水平二维平面上的微重力模拟环境,因此需要建立监测系统,实现校准过程的有效性监测,以确保标准货包的微重力模拟状态满足要求。监测系统组成如图5所示,由力传感器、三轴加速度传感器、倾角传感器、信号调理装置、信号实时采集装置和实时采集记录软件等组成。
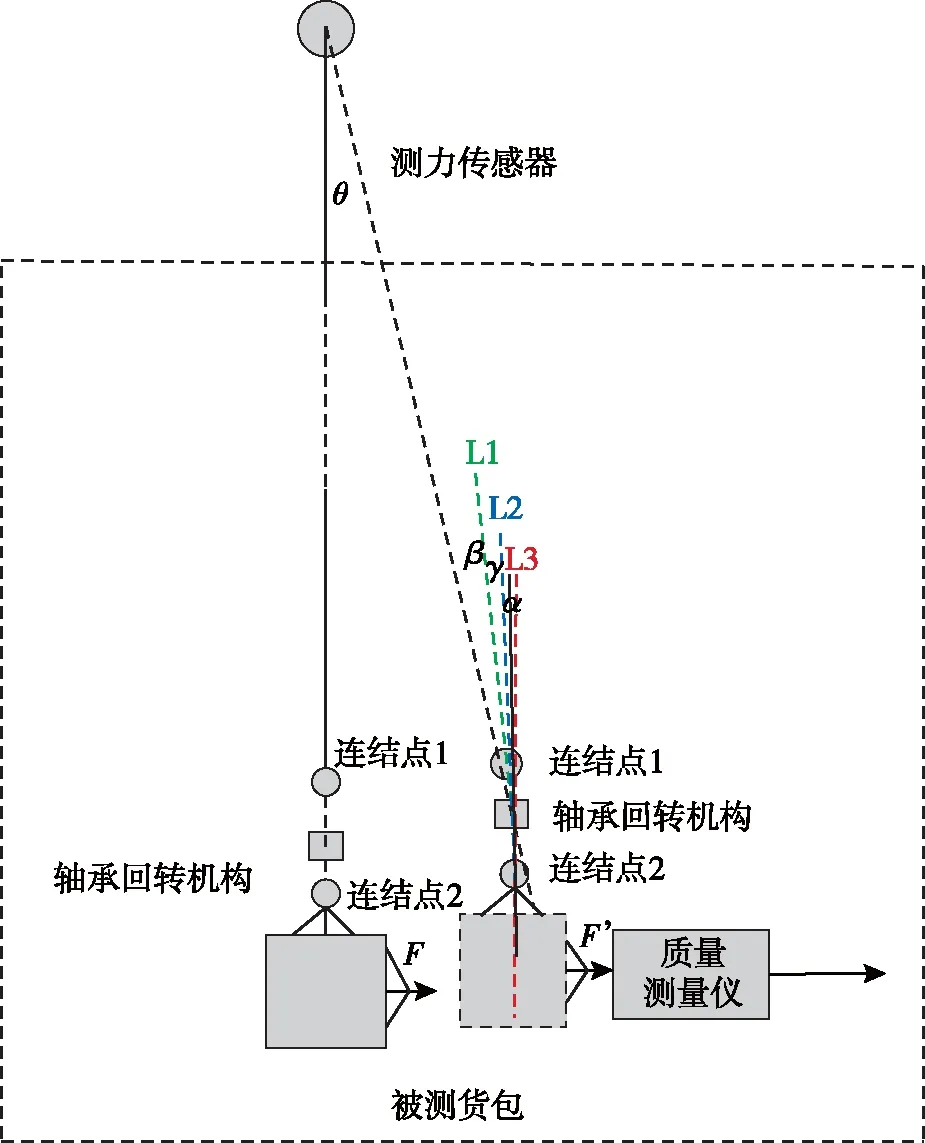
图4 悬吊机构示意图Fig.4 Suspension mechanism schematic
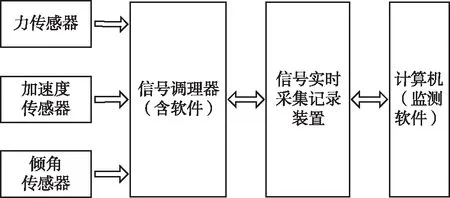
图5 实时采集记录系统组成框图Fig.5 Block diagram of real-time acquisition and recording system
4 校准装置不确定度分析
4.1 测量不确定度
在轨质量测量仪地面校准装置测量不确定度来源主要有以下几项。
1)校准用标准货包引入的相对不确定度u
校准用标准货包质量值引入的不确定度为标准货包校准不确定度,货包校准的不确定度为0.1%(k
=2),因此u
=0.
1%/
2=0.
05%
2)在轨质量测量仪拉动时运行轨迹不“水平”引入的测量不确定度u
校准时,在轨质量测量仪拉动时运行轨迹“水平”主要由水平工作台决定,水平工作台的技术指标为30″,可忽略不计。
3)水平工作台高度位置不正确引入的相对不确定度u
由于水平工作台的高度位置不正确,使在轨质量测量仪的测力传感器的高度与施力绳拉直状态下的连结点不在同一高度,该项主要影响加速度,按照均匀分布进行计算
(sin(30/
3600)×9.
8/
0.
24)×100%
=0.
6%
根据式(4),加速度变化对质量测量结果的影响就是加速度的变化量,即0.6%。
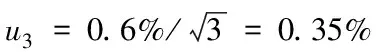
θ
引入的相对不确定度u
货包偏离悬吊平衡点的摆动角为θ
,由于重力和悬吊绳拉力作用,产生返回平衡点的力,根据“地面校准时最大加速度、最大力与偏离平衡位置关系分析”(在轨质量测量仪原理和使用说明进行分析),货包偏离悬吊平衡点的摆动角θ
及其对产生加速度的测量力的影响,见表3。5)标准质量货包变形引入的不确定度u
对货包施加的力随着货包质量的变化而呈一定的趋势变化,其力值介于(1.2~38.4)N之间,估计货包变形对加速度传感器输出的影响约0.000 1g,按照满量程最小0.24m/s计算,对货包合成加速度的最大影响为
(0.
0001×9.
8/
0.
24)×100%
=0.
41%
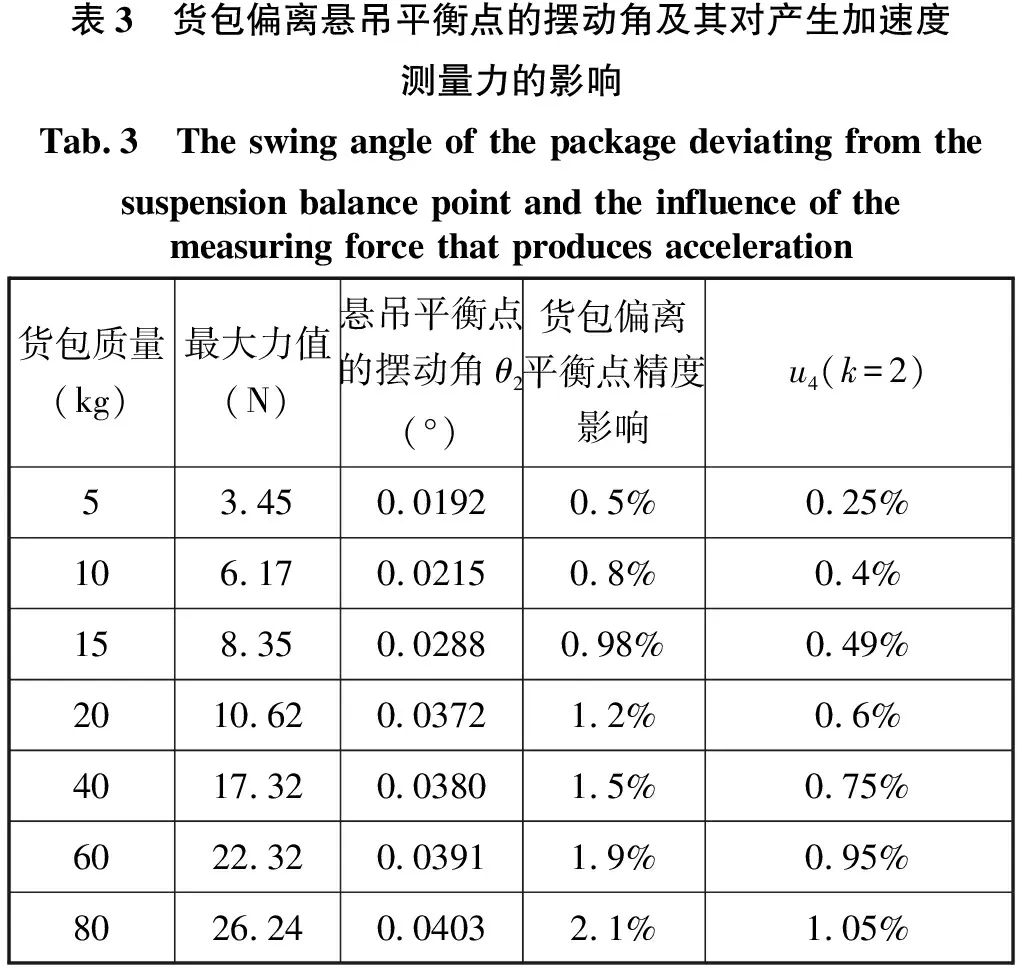
表3 货包偏离悬吊平衡点的摆动角及其对产生加速度测量力的影响Tab.3 The swing angle of the package deviating from the suspension balance point and the influence of the measuring force that produces acceleration货包质量(kg)最大力值(N)悬吊平衡点的摆动角θ2(°)货包偏离平衡点精度影响u4(k=2)53.450.01920.5%0.25%106.170.02150.8%0.4%158.350.02880.98%0.49%2010.620.03721.2%0.6%4017.320.03801.5%0.75%6022.320.03911.9%0.95%8026.240.04032.1%1.05%
根据式(4),加速度变化对质量测量结果的影响就是加速度的变化量,即0.41%。
按均匀分布计算,引入的测量不确定度u
为
u
按照悬吊高度为20m,不考虑绳长的变化,货包在拉动过程中由于高度的上升引起重力方向上的加速度变化,按照0.1m水平摆动,货包向上抬升小于1mm,因此对加速度的影响可忽略不计。
7)校准过程中环境及装置运动结构变化引起加速度变化引入的测量不确定度u
采用高塔悬吊方式,校准过程中悬吊绳质量的变化、环境变化(风、振动噪声)、装置中运动结构变化等引起的水平加速度的变化,以及校准环境中电磁噪声引起的加速度传感器信号输出的变化,根据监测系统要求,不超过量程的0.1%,货包水平最小加速度为0.24m/s,按均匀分布计算,则加速度变化引入的测量不确定度为
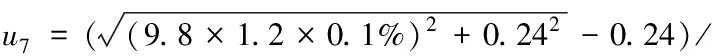
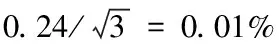
根据式(4),加速度变化对质量测量结果的影响就是加速度的变化量,即0.01%
8)悬吊绳、挂钩质量等引入的测量不确定度u
由于悬吊绳、挂钩等具有一定的质量,拉动货包使货包摆动,水平拉力使挂钩及悬吊绳具有一定的加速度,按照悬吊绳质量均分,悬吊绳从顶端到悬吊货包的底端的加速度从0到货包的加速度均匀变化,这算到对货包质量的测量的影响,可忽略不计,主要是挂钩及附件的影响,挂钩约为0.16kg,按照均匀分布,因此引入的测量不确定度u
,见表4。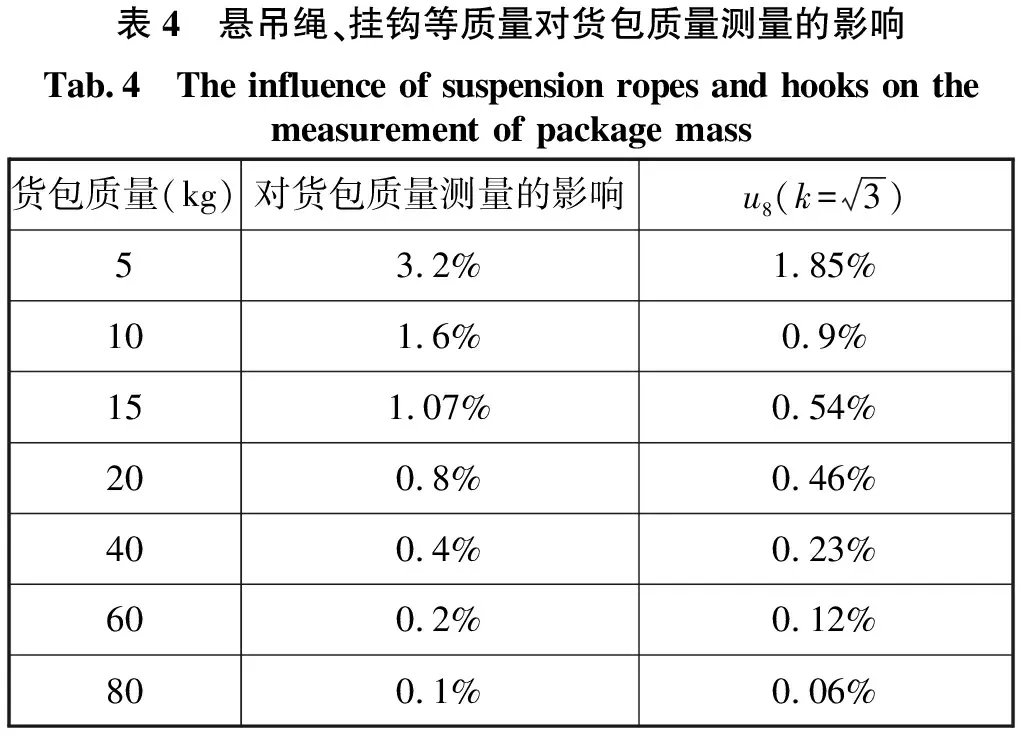
表4 悬吊绳、挂钩等质量对货包质量测量的影响Tab.4 The influence of suspension ropes and hooks on the measurement of package mass货包质量(kg)对货包质量测量的影响u8(k=3)53.2%1.85%101.6%0.9%151.07%0.54%200.8%0.46%400.4%0.23%600.2%0.12%800.1%0.06%
4.2 合成标准不确定度
以上各标准不确定度分量互相独立,测量范围为(5~15)kg,则其合成标准不确定度u
为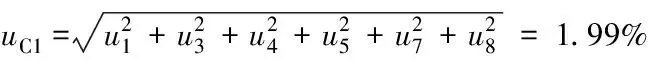
u
为
4.3 相对扩展不确定度
测量范围为(5~15)kg,示值误差的相对扩展不确定度为
U
=ku
=3.
98%
(k
=2)测量范围为(15~80)kg,示值误差的相对扩展不确定度为
U
=ku
=2.
52%
(k
=2)5 结束语
本文介绍了在轨质量测量仪地面校准方法,并基于该方法研制了地面校准装置,详细分析了校准装置的测量不确定度,并对七种不同规格的标准质量货包进行了地面校准试验,试验结果表明采用高塔悬吊标准货包的方式,在水平二维平面上建立微重力模拟环境,可以实现在轨质量测量仪的地面校准,为后续货运飞船用在轨质量测量仪装船前地面校准提供数据。
