基于小波分析的火箭发动机试验流量数据去噪处理

杨 懿 李达银 郭亚男 贾志杰 王永鹏

(北京航天试验技术研究所，北京 100074)

1 引 言

在氢氧火箭发动机试验中，推进剂的流量数据是计算发动机比冲、评估推力性能等关键指标的重要依据，也是试验中的关键参数之一。在某次发动机试验过程中，流量参数采集系统受到未知干扰，液氧流量数据包含有大量的噪声成分。鉴于试验的不可重复性，需要对液氧流量数据进行去噪处理。

在工程应用领域，基于小波分析理论的去噪方法在数字信号去噪处理领域有着十分广泛的应用，其去噪的方法主要有频域低通滤波去噪、模极大值去噪、小波包去噪和小波阈值去噪等几种方法。杨懿等采用不同的小波阈值去噪法，选取Db9小波和Mallat分解重构算法对液体火箭发动机启动段振动信号进行去噪，但是并没有对比其他小波基函数的去噪效果。马栋梁等通过分析不同小波基函数的评价指标，有针对性地选取小波基函数。但鉴于其分析信号的特殊性，该去噪方法只适用超临界水自然循环流量信号。赵宇翔等分析了多种小波基函数的特点和四种阈值设置规则对数据去噪效果。方海荣通过对比两类不同小波系的信号处理的信噪比，采用了信噪比较大的两种小波基函数对含噪信号进行处理，最大程度还原了原始信号，实现了信号的去噪处理。

本文采用自适应阈值(Rigrsure)和Db9基函数的组合小波阈值去噪法对含噪液氧流量数据进行去噪处理，结果表明该方法能有效消除流量信号中的噪声成分。

2 流量系统组成

在该次试验中，流量测量系统由涡轮流量计、信号发生器、流量预处理仪和数据采集系统组成。系统基本组成图如图1所示。

图1 流量系统组成图

2.1 涡轮流量系统测量原理

涡轮流量系统的基本原理是：被测介质推动涡轮流量计叶轮旋转，叶轮切割流量计外部的永磁体信号发生器的磁力线并产生正弦波式感生电动势。感生电动势的频率与流体的流速、叶轮的转速成正比。当管路横截面积不变时，流体的流速与流量成正比例关系。感应电势的频率

f

和被测流量

Q

的线性关系可由式(1)表示：

Q

=

A

+

Bf

(1)

式中：

Q

——通过传感器的容积流量，单位：L/s；

A

——传感器常数；

B

——传感器系数;

f

——传感器输出频率，单位：Hz。

3 小波分析基本原理及去噪方法

小波分析方法是近些年来非常流行的一种数字信号处理方法。该方法具有低熵性、多分辨率的特点，相比傅里叶变换，该方法最大的优势是可根据被分析信号的特点灵活选择多种各具特点的基函数对信号进行分析处理，既可分析信号的局部特征，其窗口大小又灵活变化，非常适合处理非稳定信号。在消除信号和图像噪声、提取特征信号、信号压缩等方面得到广泛的应用。

3.1 小波变换的基本原理

小波变换以傅里叶变换为基础，弥补了傅里叶变换中高次谐波三角基函数无法在时域上对信号进行分析的缺点，利用小波基函数参数的伸缩、平移的多尺度变化，使小波基函数具有波动性、衰减性的优良特性，能够对信号分别在高频部分和低频部分在时间域和频域进行多尺度的细化分析。小波去噪方法中，连续小波变换、离散小波变换和离散小波变换分解与重构是其核心的理论。

为了便于计算机进行计算分析，需要将连续小波函数、伸缩系数和平移系数离散化。离散化的方法通常把伸缩系数和平移系数取幂级数。对信号进行小波离散后需要进行多重分解与重构。工程应用中，常用Mallat算法将信号分解为多尺度低频小波系数和高频小波系数。小波重构则是小波分解的逆运算，将高、低频小波系数按Mallat算法中的重构公式进行重构。

3.2 小波去噪原理

小波变换信号去噪的基本原理是将含噪的信号看作原始信号和含噪信号的叠加。真实信号一般集中体现在一些高频系数中，而噪声的能量则几乎分布在整个小波域内。通过对含噪信号进行小波多层分解能得到不同的高频系数，该高频系数可以看作是原始信号高频系数和噪声信号高频系数的叠加。一般而言，信号的系数要高于噪声的系数。因此在实际的操作中可以采用小波变换对信号进行多层分解，在保留低频系数的同时，对各高频层的系数进行去噪处理，然后再对小波系数进行逆变换重构，实现对含噪数据的去噪处理。

3.3 小波阈值去噪以及评价指标

由前文的介绍可知，通过对含噪信号进行小波变换得到的高频系数可以看作是原始信号的高频系数和噪声信号的高频系数叠加，且原始信号的系数(假设等于α)一般要大于噪声信号(假设等于β)的系数。通过设定阈值γ，使得β<γ<α。当分解含噪信号得到的系数值<γ时，将该信号视为噪声信号，在处理时将该系数置0。当分解含噪信号得到的系数值>γ时，将该信号视为原始信号，同时保留该小波系数，最后重构处理完的小波系数。

小波阈值去噪法一般有两种方法。一种为硬阈值法(例如强制去噪法)。当小波系数<设定阈值γ时，将系数置零。当系数>设定阈值γ时，保持系数不变。另一种为软阈值法(例如默认阈值法)。当小波系数<设定阈值γ时，系数置零。当系数>设定阈值γ时，将系数减去给定阈值。软、硬阈值去噪法各有其优缺点。硬阈值法处理时因为不连续容易导致重构信号出现伪吉布斯现象，去噪后产生震荡信号，丧失初始信号的平滑性。软阈值处理时，虽然曲线是连续的，但由于阈值的设置不合理，得到的曲线与实际信号之间还是存在一定差别。

实际应用中常用4种阈值设置规则，分别是固定阈值法(Sqtwolog)、自适应阈值选择的无偏似然估计法(Rigrsure)、启发式阈值选择法(Heursure)和极大极小原理选择阈值法(Minimaxi)。4种规则各有特点。在工程应用中对非平稳信号的处理时多采用Rigrsure与 Heursure阈值设置规则。但是两种方法也有各自的弊端。Heursure阈值规则将全部小波系数进行处理，很容易去噪过度，丢失有用信息，因此比较适合处理高频分量多的信号。Rigrsure阈值规相对而言要保守一些，仅仅将部分系数置零，在完成去噪的同时，能更大程度地保存有用信息。

工程应用中主要采用信噪比、均方根误差、相关系数等指标评价数据去噪的效果。其中信噪比和相关系数是两个最重要的指标。信噪比是信号功率与噪声功率的比值，比值越大说明去噪的效果越好。相关系数是指去噪后的信号与原始信号特征信息的相似程度。相关系数值越大，表明相似度越高，去噪的效果越好。

3.4 小波基函数的选择原则

在工程应用中，常用的小波基函数有：Haar函数、DbN函数、SymN函数、CoifN函数和Dmey 函数。各种基函数都有自身的特点，使用的基函数不同，得到的处理结果也不一样。在实际的运用过程中需要根据数据和小波基函数自身的特点，选择合适小波基函数进行数据处理。

小波基函数的选取主要遵循以下几点原则。

1)支撑长度。支撑长度是指当时间或频率趋近无穷大时，尺度函数、小波函数及其傅里叶变换从有限值收敛到0的速度。

2)对称性。对称性能够有效避免信号处理中的移相问题。

3)正则性和消失矩。正则性和消失矩呈正相关关系，主要影响小波系数重构的稳定性。

各种小波基函数的特点如表1所示。

表1 各小波基函数特点Table.1 CharacteristicsofwaveletbasisfunctionsHaar函数DbN函数SymN函数CoifN函数Dmey函数正交、紧支撑、单个矩形波、矩形状阶梯变化、计算简单正则性好、对称性好、频域的局部化能力强、频带划分效果好、紧支撑、消失矩光滑性好DbN函数的一种改进、具备DbN函数的优点、对称性比Db函数好对称性比Db函数好不具备紧支撑性、收敛速度快

3.5 小波阈值去噪的基本步骤

小波阈值去噪过程一般分为以下几个步骤。

1)确定所采用的阈值处理方法(软阈值法或者硬阈值法)。

2)选择小波基函数。

3)确定分解层次。

4)确定阈值设置规则。

5)对小波分解系数进行阈值量化处理。

6)对分解系数进行重构。

在以上步骤中，选择合适的小波基函数和阈值的量化处理是最为重要的环节，直接关系到信号处理的质量。

4 液氧流量数据去噪

在某次发动机试验中，含噪液氧流量(Qo)数据全程和局部数据分别如图2、3所示。选取4500个样本点作为去噪分析的原始数据。

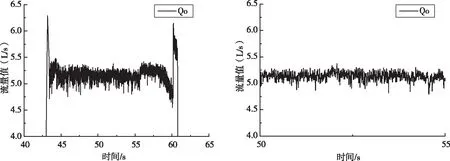
图2 全程流量数据图 图3 局部流量数据图

通过表1的分析，从Sym系和Db系各选出一种小波基函数对原始数据进行去噪处理。由于该型号试验连续两次试验流量测量系统设备完全一致，以该型号试验上一次未受噪声干扰的液氧流量数据作为对比分析的标准，计算Sym系和Db系小波基函数去噪信号的信噪比。从Sym系和Db系中各选取信噪比最优者。信噪比分析结果如表2所示。

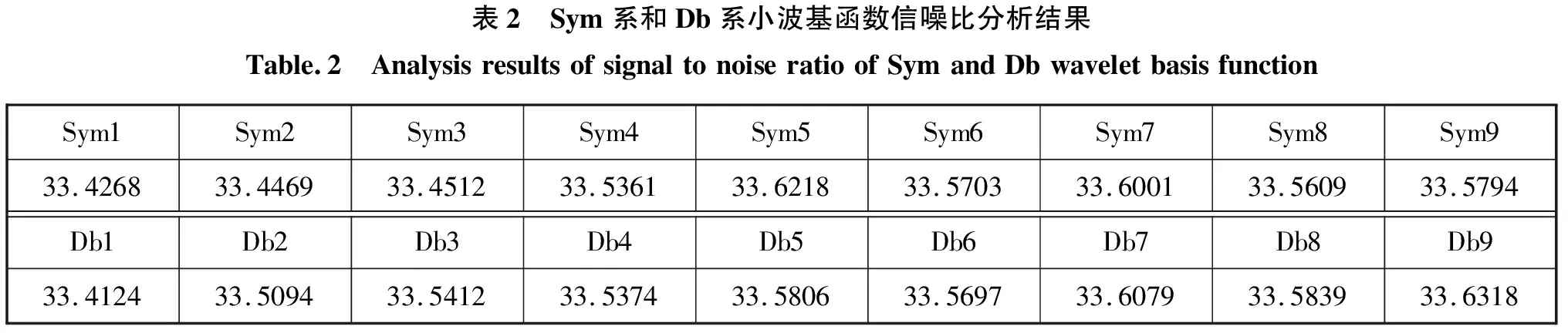
表2 Sym系和Db系小波基函数信噪比分析结果Table.2 AnalysisresultsofsignaltonoiseratioofSymandDbwaveletbasisfunctionSym1Sym2Sym3Sym4Sym5Sym6Sym7Sym8Sym933.426833.446933.451233.536133.621833.570333.600133.560933.5794Db1Db2Db3Db4Db5Db6Db7Db8Db933.412433.509433.541233.537433.580633.569733.607933.583933.6318

通过分析表2的数据结果，选用信噪比最大的Sym5和Db9小波基函数作为基函数。

对四种阈值规则的选择也采用相同的方法，通过计算流量去噪数据的信噪比选择合理的阈值规则。4种阈值规则处理数据的信噪比结果如表3所示。

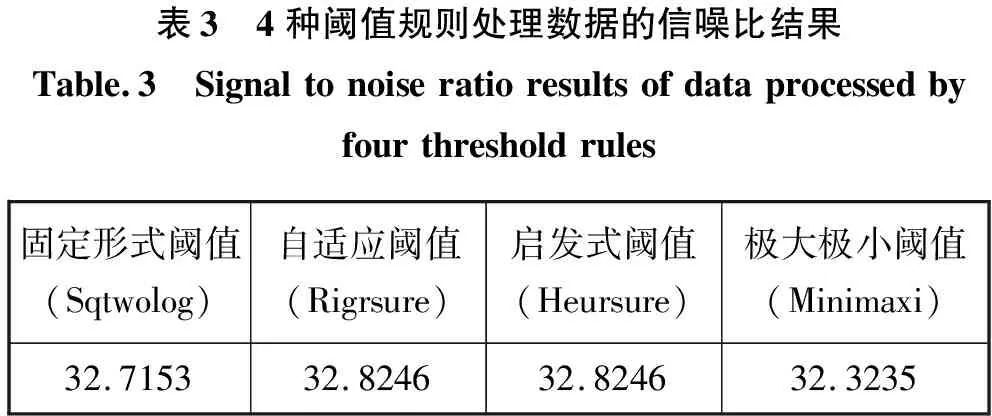
表3 4种阈值规则处理数据的信噪比结果Table.3 Signaltonoiseratioresultsofdataprocessedbyfourthresholdrules固定形式阈值(Sqtwolog)自适应阈值(Rigrsure)启发式阈值(Heursure)极大极小阈值(Minimaxi)32.715332.824632.824632.3235

通过分析表3的数据结果，Rigrsure和Heursure的信噪比最大，因此分别采用这两种阈值设置规则方便进行分析对比。

数据处理方法：选用Sym5和Db9小波基函数作为基函数，采用Rigrsure和Heursure两种阈值设置规则，分别采用三层分解、重构和五层分解、重构方法对数据进行对比分析，对处理后的数据采用信噪比和相关系数作为评判指标。数据处理结果如图4、5所示。

从图4和图5的分析结果可以看出，由于强制去噪小波分解后的高频系数全部置零，过滤掉了所有的高频成分强制，去噪方法比默认去噪方法去除噪更加彻底，去噪后的曲线比较平滑，但是也过滤掉了信号中的一些有用信息。三层分解、重构时，Sym5和Db9 小波基函数在Rigrsure和Heursure两种阈值规则下的分析结果从图像上很难分辨出优势。分别对三层分解重构和五层分解重构后的数据进行信噪比和相关系数计算，对比两种阈值设置规则的优劣。计算结果如表4所示。

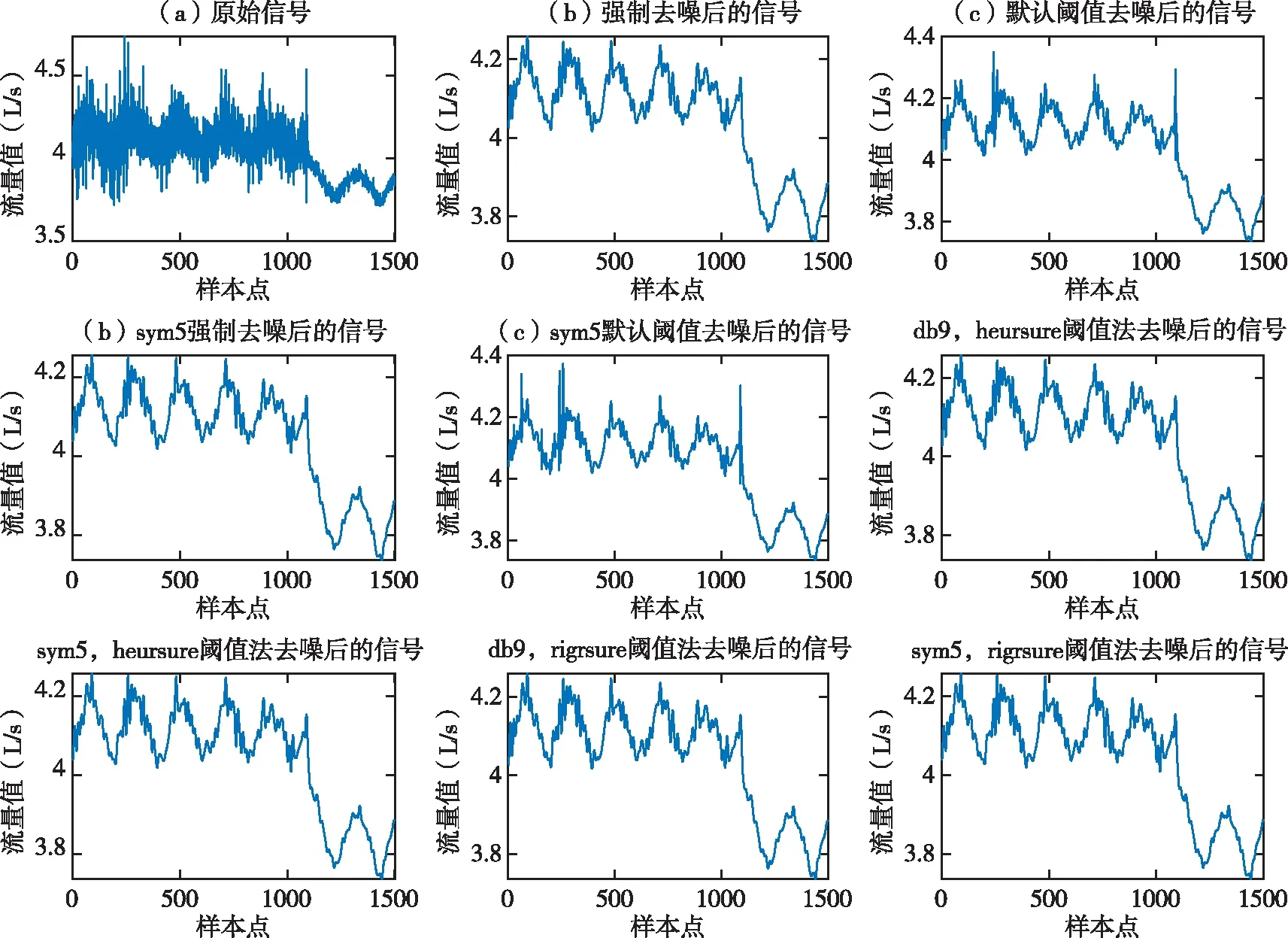
图4 三层分解、重构效果图

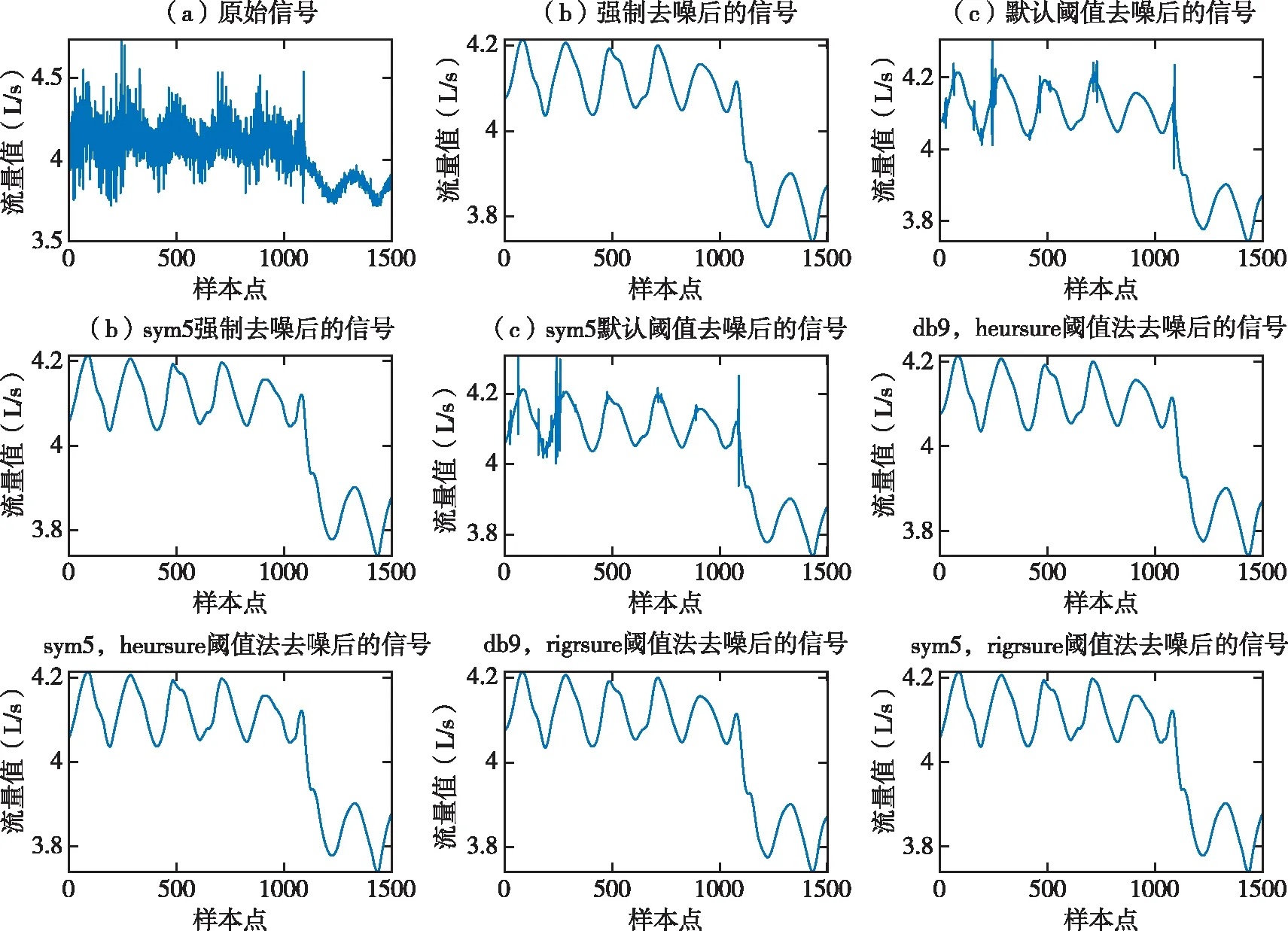
图5 五层分解、重构效果图

表4 阈值和分解层数组合下去噪信号的信噪比和相关系数值Table.4 Signaltonoiseratioandcorrelationcoefficientofdenoisingsignalcombinedwiththresholdanddecompositionlevel阈值选取规则和小波基函数三层分解、重构五层分解、重构信噪比(DB)相关系数信噪比(DB)相关系数强制去噪,Db922.52170.641222.30110.6293默认阈值,Db922.51970.634522.20990.6026强制去噪,Sym522.51950.641122.3070.6297默认阈值,Sym522.50460.628922.28150.6075Heursure,Db922.52110.640822.30010.6290Rigrsure,Db922.52170.641222.30110.6293Heursure,Sym522.51950.641122.3070.6297Rigrsure,Sym522.51950.641122.3070.6297

从表4可得出，三层分解重构方法中，选择自适应阈值(Rigrsure)和Db9基函数得到的信噪比和相关系数最大，处理后的数据效果最好。在五层分解重构方法中，自适应阈值(Rigrsure)和Db9基函数的信噪比最大，但是相关系数比(Heursure+Sym5)组合和(Rigrsure+Sym5)组合要略小。(Heursure+Sym5)组合和(Rigrsure+Sym5)的结果一致。三层分解重构的信噪比、相关系数比五层分解重构的信噪比、相关系数都要大，但是五层分解重构的曲线更加光滑。这是因为五层分解、重构后的数据过滤掉了更多的信息。因此，为最大程度保留原始数据的有用信息，选取(Rigrsure+Db9基函数)组合，采用三层分解、重构方法作为液氧流量去噪的方法。分析流量计上下游的压力、温度数据，结合液氧密度、管径等参数，计算理论流量数值。分别选取分析样本点的第200、400、600、800、1000、1200六个样本点的数据进行计算验证，与设计部门提供的设计数据进行对比分析。验证情况如表5所示。

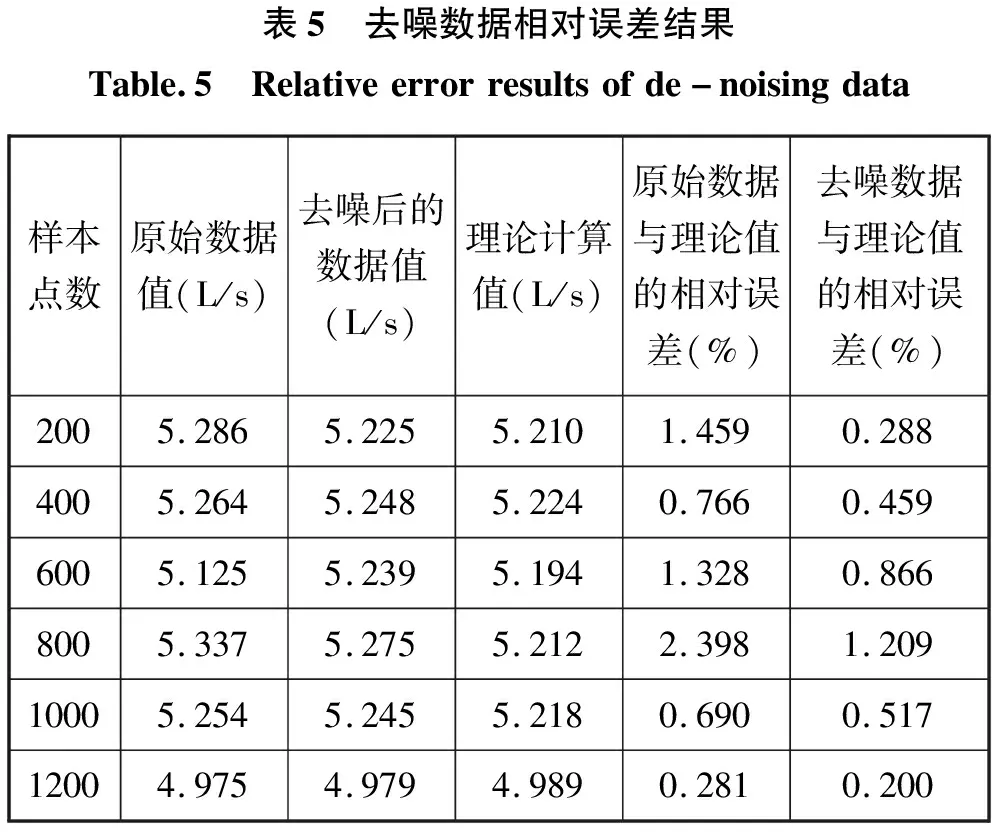
表5 去噪数据相对误差结果Table.5 Relativeerrorresultsofde-noisingdata样本点数原始数据值(L/s)去噪后的数据值(L/s)理论计算值(L/s)原始数据与理论值的相对误差(%)去噪数据与理论值的相对误差(%)2005.2865.2255.2101.4590.2884005.2645.2485.2240.7660.4596005.1255.2395.1941.3280.8668005.3375.2755.2122.3981.20910005.2545.2455.2180.6900.51712004.9754.9794.9890.2810.200

5 结束语

本文介绍了基于小波变换阈值去噪理论的某型号液体火箭发动机试验液氧流量信号的去噪方法。通过分析各小波基函数的特点，研究硬、软阈值法和软阈值法的四种阈值设置规则的特点，采用Sym5、Db9小波基函数和Rigrsure、Heursure两种阈值设置规则的组合对含噪液氧流量信号进行去噪处理。将信噪比和相关系数值作为去噪效果考核指标，分析结果与设计部门的理论计算值的相对误差分析显示，Rigrsure和Db9基函数的组合，采用三层分解重构方法的去噪效果较好。该方法在氢氧火箭发动试验其他参数数据去噪分析领域具有十分重要的应用和推广意义。