吠陀历中的置闰缘由及日月位置推算方法

吕 鹏 纪志刚

(上海交通大学 马克思主义学院 科学史与科学文化研究院，上海 200240)

1 文献背景及前人研究

2 吠陀历内容及其置闰方法

(1)太阳尺度，以太阳与星宿(冬至点)的会合周期为标准，包含太阳北行南行两个阶段；

(2)太阴尺度，以朔望月周期为标准，一个朔望月又分为月亮渐盈的“白分”和渐亏的“黑分”这两个半月；

(3)恒星尺度，以星宿的地平线初升为标准，一周天(黄道)均分为27宿；

(4)历日尺度，以日出地平为标准，相连两次日出之间的间隔为一历日。

关于年月日，下面的诗偈说道：

RJ1=YJ1：我低头向生主(Prajpati)——他是由5年所构成的纪的主，并以[历]日、季节、[太阳的]行和[朔望]月为肢体——敬礼后……

RJ4=YJ13：[现在的年数]减去1，乘以12，2倍后加上[今年中]经过的[半月数]，每60再加上2，所得的就是[从纪的开始时所经过的]半月(parvan)数。

RJ18：月亮与某个星宿的结合[的日数]为1日又7小分(kalā)，太阳则为13又9分之5日。

上面第一偈诗首先明示了1纪的长度为5年，之后的一偈则给出了求从纪元起到任意时候经过的半月个数的计算方法。若取5年为现在的年数，则1纪中所包含的半月个数就为：

5 × 12 × 2+4=124

即相当于62个朔望月。其中每60再加上2透露出吠陀历采取每30个月插入1个闰月，或者说是5年2闰的置闰方法。

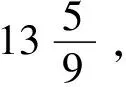
RJ33：三日、九日、望日，以及黑分的六日、十二日为[昼夜]平分的日期，[这之后的平分日期]和之前的一样。

VJ11：将最初的作为之前的，后继的季节变换的日期将会隔一月又一日。……第8个[季节变换的日期]发生在[白分的]第十五日。

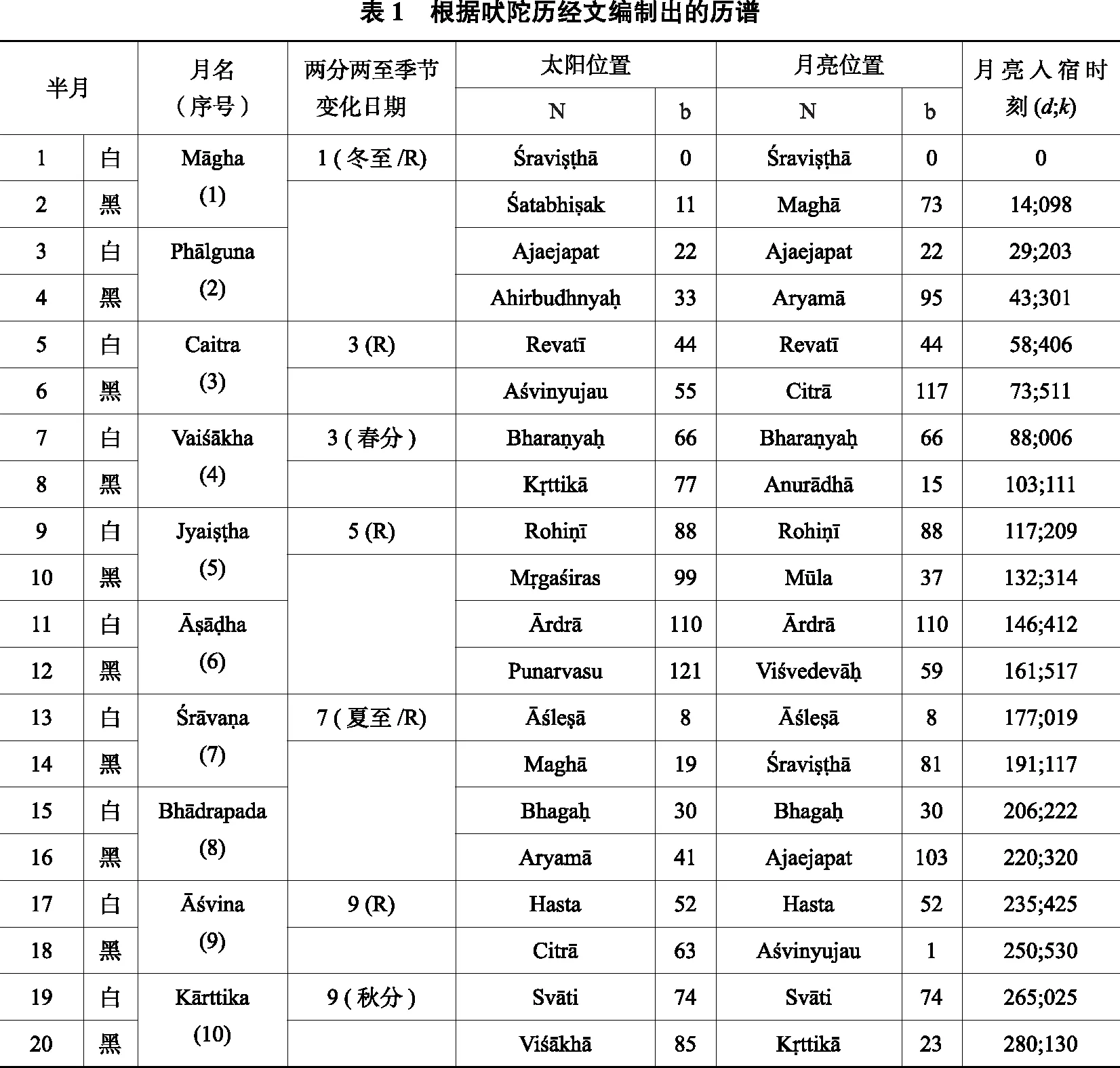
略加计算，我们就可以知道吠陀历中两分两至的日期，以及一年6个季节的变换日期(R)(7)印度各文献中对季节的划分并不一致，有3、5、6、7、12、13和24这几种划分。吠陀历规定2个月为一季，一年共有6个季，从Caitra月开始依次为春季、夏季、雨季、秋季、冬季和寒季。，据此我们可以编制出如表1的吠陀历谱。

2.20.66偈：……每隔两年半产生一个闰月，第一个设在[第三年的]夏季，第二个则是在五年[纪]的末尾。([8]，269页)

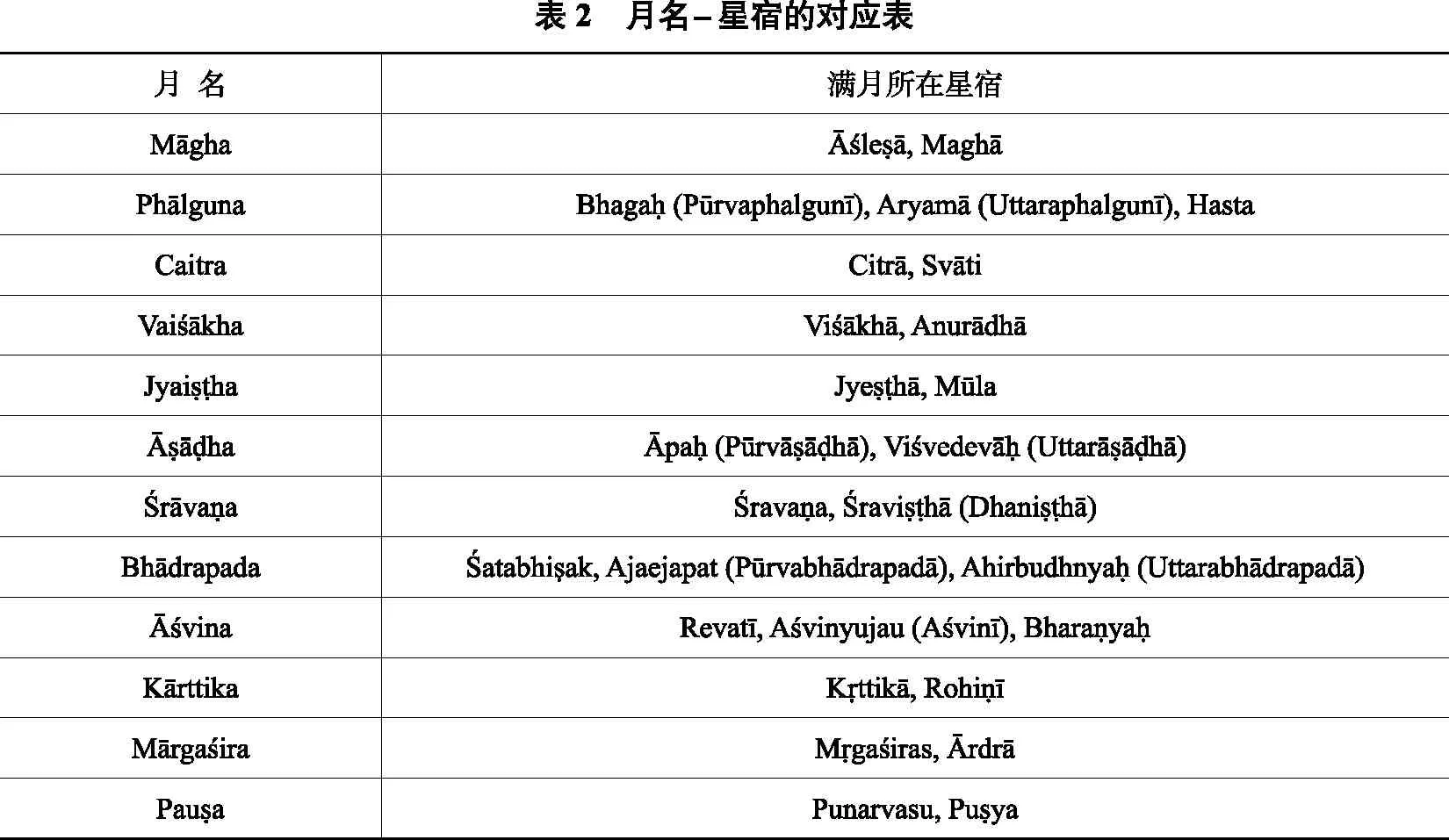
然而，对于吠陀历为何采用这种置闰方法，以往的研究都没有做出详细说明。根据上面的历谱可以看出，其实这种置闰方法是和吠陀历中的月名有着密切的关系。

3 计算昼夜长度、日月位置和入宿时刻

前面已经谈到，吠陀支天文学中提供了许多算法可以用来确定每日昼夜长度、推算太阳和月亮在星宿间的位置、计算月亮进入某个特定星宿的时刻等等。下面就以这三项为例详细说明。

(1)昼夜长度算法。有以下诗偈：

RJ7=YJ8：当[太阳]北行时，[每天]白天[的时长]增加水[钟的]一普拉斯它(prastha)[的重量]，夜晚则减少；当南行时则相反。[相隔]一行则相差6牟乎栗特。

RJ22=YJ40：将太阳北行的半年中经过的日数，或南行半年剩下的日数乘以2除以61，再加上12后就是白天的时长。

吠陀历以及后世印度中世历法中均将一历日平均分为30牟乎栗特(muhūrta，也译为“须臾”)。已知一年两行包含366个历日，一行为183个历日。如果某日距离太阳北行开始时(即冬至日)经过了d天，则该日白天的长度l可以从下面的函数求出：

当该日正好是冬至日时，d为0，白天长度就等于12牟乎栗特；夏至日时，d为一行的天数183，白天长度计算出为18牟乎栗特。所以说一行则相差6牟乎栗特(9)冬至日和夏至日相差6muhūrta，或4.8小时所对应的地区的纬度约在35°到36°之间。，再者也验证了RJ18偈中所做的历日天数计算的正确。

RJ10=YJ15：[太阳的]入宿度应当如此计算：每经过12个半月，取8；未满时乘以11。若求白分结束时月亮的[入宿度]，则加上[星宿的]一半。

倘若从纪元起经过p个半月，对于太阳由上面分析已知，当p<12时，b应为11的倍数，所以说未满时乘以11；而当p=12或是12的倍数时，b为8的倍数，即每经过12个半月，取8。合并两种情形，用式子表示的话得到：

对于月亮来说，如果p是偶数，即p对应的是白分的开始，那么月亮的入宿度和太阳的相等；如果p是奇数，对应的是黑分，月亮的入宿度等于太阳的入宿度加上[星宿的]一半，即62度。

紧接着，根据得到的入宿度b，通过下面的方法可以巧妙地知道太阳和月亮所在的星宿：

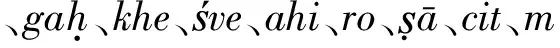
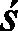
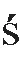
将入宿度b=1代入，得到一个可以用如下二元一次不定方程表示的不定问题：

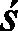
上面推导过程中所用到的三量法在吠陀支天文学文献中已有记述([10]，133页)，但我们无法肯定当时吠陀历算家们是否也掌握了库塔卡算法。印度文献中最早记载库塔卡的是5世纪阿耶波多的《阿耶波多历算书》，接着7世纪婆罗摩笈多、9世纪马哈维拉，一直到12世纪的婆什迦罗二世都继承和发展了这个算法。细读他们的著作可以知道，阿耶波多等人对于库塔卡算法的兴趣就直接来源于天文计算的需要([10]，163页)。因而我们这里提供的“三量法-库塔卡方法”不仅是对RJ14偈的数学推导和证明，或可作为吠陀历算家编制历谱的复原方法。

(3)通过入宿度b，计算月亮进入星宿的时刻。

RJ11=YJ19：占据的度数中每8度当计19小分，占据的度数不足时将未满的量乘以73，再[从总的小分数中]减去。

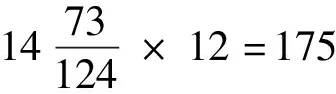
根据上式计算所得结果k可在表1历谱中查出。同时当日经过的历日数d也在历谱中予以给出。

4 结 语

另外，从之前的解读分析我们还留意到吠陀支天文学的一个特点，即其中一些关键事项和数值都被叙述了两次，或是实际能用两种不同的方法推导出来。我们猜测这也可能是历算家们有意为之，目的是通过数值的互相印证来保证吠陀历在口耳相传的传承过程中不至于改变。

致 谢感谢匿名专家和主编邹大海研究员的宝贵审稿意见。感谢西北大学辛佳岱博士在本论文修改期间的讨论与建议。