基于滑动窗口的时间序列异常检测方法

田 腾，石茂林，宋学官，马 跃，冯翔宇

(大连理工大学机械工程学院，辽宁大连 116024)

0 引言

随着物联网和检测技术的发展，工程系统中的大量时间序列数据被记录下来，挖掘这类数据对于提升工程系统的设计、分析、运行和维护水平具有重要的意义[1-2]。然而，受制于检测系统的精度和工程系统嘈杂的作业环境，所获得的工程数据往往存在大量噪声或异常数据[3-5]。因此，在进行数据挖掘与分析之前，就有必要进行数据的异常识别与归类。

目前，时间序列的异常值检测方法主要包括基于统计的方法[6-7]、基于时序模型的方法[8]、基于滑动窗口[9]的方法。相比于其他方法，基于滑动窗口的方法能够对时间序列进行分割，实现时间序列数据的降维处理，降低了计算复杂度，同时该方法便于理解规则又计算简单[10]，因此得到了广泛应用。基于滑动窗口的检测方法常用的子序列特征指标有：数据的空间距离、数据的统计分布和数据的斜率。然而基于数据空间距离、数据的统计分布的方式存在数据中心难以有效提取[11-12]、难以描述子序列数据结构特征[13-14]的问题，基于数据斜率的方式能够反映数据的结构变化，进而得到了研究人员更多的关注。文献[15]计算子序列内相邻两点的斜率与设定的斜率范围进行比较，以此判断异常值，实现了电流信号的异常检测。文献[16]分别计算目标点与前、后数据的斜率进行异常判断，实现了电网异常数据的检测。文献[17]计算子序列内的最后一点与第一点的斜率变化作为子序列的特征信息，借助K-Mean实现异常检测。文献[18]采用子序列的斜率、均值、极值差等信息对子序列进行分段线性表示，使用层次聚类算法实现了水文异常数据的检测。文献[19]采用最小二乘法拟合序列斜率，根据斜率的相对变化值判定异常数据，实现了大型立式磨床的故障预警。

工程数据中异常数据分布随机性大、波动性大，而基于斜率的传统检测方法存在数据形态信息利用率低、数据结构特征描述不全面、特征提取不准确等弊端，导致其难以适用于工程数据的异常检测。为此，本文采用基于子序列斜率的置信区间的方式进行特征提取，并提出基于滑动窗口的时间序列异常检测方法。仿真数据检测结果表明，本文的方法提高了检测精度。工程数据的异常检测实验表明，提出的算法能够准确检测异常值信息，能够胜任工程数据的检测工作。

1 基于滑动窗口的时间序列异常检测方法

该方法首先将时序数据分割为若干个子序列，随后提取子序列的数据特征并用于识别异常子序列，最后采用Gath-Geva聚类算法识别异常子序列中的异常值。具体步骤介绍如下。

1.1 子序列分割

一条时间长度为n的时间序列表示为

Y=(y(t1),y(t2),…,y(tn))

式中y(ti)为ti时刻记录的数据，采集时间ti是严格增加的。

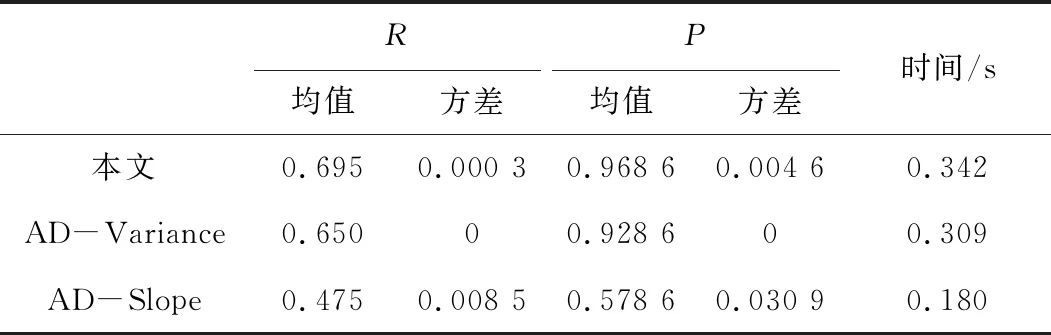
在时间序列的子序列分割中，采用长度为l(l<

图1 滑动窗口工作原理图

1.2 子序列特征提取与识别

置信区间是数据统计分析中常用的技术手段，能够以一定的可靠程度估计总体数据的所在区间。斜率能够表述子序列的结构特征，但是斜率信息分布随机，为了准确描述子序列斜率信息分布情况，采用斜率的置信区间距离半径作为子序列的特征表示，特征提取步骤如下。

假设其中某一个子序列为Yj(1≤j≤(n-l)/r+1)，根据式(1)计算该子序列中任意相邻2个数据点之间的斜率：

(1)

则在该子序列Yj中，共得到l-1个斜率值，可得斜率的置信区间距离半径为

(2)

置信上限为

(3)

置信下限为

(4)

基于提取的子序列特征，给出疑似异常子序列的判断模型：假设含有n个变量的时间序列Y=(y(t1),y(t2),…,y(tn))，存在第j个子序列yj(1≤j≤(n-l)/r+1)斜率的置信区间距离半径dj>γ，其中γ为阈值，则认为时间序列Y中的第j个子序列yj为异常子序列，其中含有异常值，待进一步实现异常值与正常值的归类。

1.3 Gath-Geva聚类算法识别异常值

针对每个识别出的异常子序列，采用GG聚类算法对数据进行划分，将异常值与正常值进行归类。

设聚类样本集合X={x1,x2，…，xN}，现将数据X划分为C类(2≤C≤N)，设其聚类中心为V={v1,v2,v3，…，vC}；设隶属度矩阵为U=[uik]C×N，其中元素uik∈[0,1]代表第k个样本数据属于第i个簇的概率(1≤k≤N,1≤i≤C)。通过迭代调整(U，V)使目标函数取得最小值：

(5)

具体步骤如下。首先计算聚类中心V={v1,v2,v3，…，vC}:

(6)

式中h为迭代次数。

然后更新隶属度矩阵：

(7)

直到‖U(h)-U(h-1)‖<ε为止，其中，ε为允许误差；否则继续令h=h+1，重复上述步骤，直至满足条件。

1.4 异常检测算法步骤

输入：长度为n的时间序列Y=(y(t1),y(t2),…,y(tn))，异常子序列判断阈值γ，滑动窗口长度l。

输出：时间序列Y的异常值信息。

步骤1：使用长度为l的滑动窗口对时间序列Y进行等长度的划分，分为若干子序列yj(1≤j≤(n-l)/r+1)；

步骤2：采用式(1)计算每个子序列中相邻两点的斜率变化ki，采用式(2)计算斜率的置信区间距离半径dj作为子序列特征；

步骤3：将距离半径dj与阈值γ进行比较，初步确定含有异常值的异常子序列；

步骤4：通过GG聚类算法对异常子序列进行正常值与异常值的归类与划分，输出时间序列Y中的异常值信息。

2 实验仿真

本节通过仿真数据和真实数据验证所提出的基于滑动窗口的时间序列异常检测方法的有效性，并通过如下指标评价实验结果[17]：

(1)查全率：

(8)

(2)查准率：

(9)

2.1 仿真数据验证

仿真数据集为包含4个变量的长度为800的时间序列，表示如下：

Y={y1,y2,y3,y4}

y1=-sin(1+0.5x)+e,x∈[0.05,10]；

y2=cos(1+0.5x)+e,x∈[0.05,10]；

y3=log2(1+0.5x)+e,x∈[0.05,10]；

y4=(-0.2x+1)2+e,x∈[0.05,10]。

式中：e为服从均值为0、方差为1的正态分布的随机数。

在数据集中随机插入20个异常值点Z～N(0，25)。异常点位置依次为3、9、29、60、72、164、235、244、358、475、518、540、549、565、606、614、624、652、678、704。

由于数据集中存在噪声e，插入的异常值波动较大，为防止“大数吃小数”的现象发生，在实验前对数据集进行归一化处理，如下所示：

(10)

首先研究窗口长度l对提出算法的影响。在实验中，将步长r设定为1，即每完成一个子序列特征提取，就向后移动一个数据点。图2为不同窗口长度条件下的实验结果，从图2中可以看出，所得结果的查全率和查准率均随着窗口长度的增加而呈现先增长后下降的变化趋势；在窗口长度l∈[7,11]时，实验结果趋于平稳。解释如下：当窗口长度较小时，子序列中的相邻数据点数量较少，导致难以通过数据斜率变化信息获取子序列精确的内部特征，从而导致子序列特征提取不准确，进而造成检测精度较低；当窗口长度l∈[9,11]时，子序列的数据量充足，能够以斜率信息准确表示子序列的数据形态，通过GG聚类能够精准识别异常值，因此查准率最高；当窗口长度l>11时，查全率R以及查准率P呈现下降趋势，主要是因为检测出的异常子序列中包含的数据较多，在异常子序列中不仅包含异常值，而且还包含了若干相邻的正常值，当通过GG聚类算法进行数据划分时，容易将部分正常值划分为异常值，也容易将少量异常值划分为正常值，因此查全率、查准率降低。综合考虑以上实验结果，最终滑动窗口长度选取为7，异常子序列判断结果如图3所示。图4为删除异常值以后的时间序列，可以看出，删除异常值后的时间序列数据变得更加平稳，数据流中并未出现较大的峰值。

图2 滑动窗口长度l对异常检测的影响

图3 异常子序列判断结果图

图4 删除异常值后的时间序列

表1中显示的不同检测算法的检测结果，对比方法分别为文献[13]提出的基于方差的时间序列异常检测方法(AD-Variance)、文献[17]提出的基于斜率的数据异常检测方法(AD-Slope)，滑动窗口长度设定为7。由于子序列特征提取方式不一致，造成子序列特征数据分布存在一定的差异，为准确识别异常子序列，分别设定最优阈值：本方法阈值为γ=0.1，AD-Variance方法阈值为γ=0.05，AD-Slope方法阈值为γ=0.03，10次重复实验结果如表1所示。

表1 不同检测算法结果

从表1中的R、P值的方差信息来看，本文方法以及AD-Slope方法都出现了小幅波动，而AD-Variance方法方差为0。AD-Variance方法仅从阈值判断异常值，所以当阈值设置完毕以后，就不会出现任何的波动情况，所以其方差为0。而本文方法和AD-Slope方法均采用聚类算法进行异常值的划分，而聚类算法结果受随机生成的初始矩阵影响，导致检测结果存在一定的波动。本文方法的方差数值小于AD-Slope方法结果，表明GG聚类算法与K-Mean算法相比运行结果更稳定。AD-Variance方法采用了置信区间的阈值判断，方法较为简单，所以其运行成本优于本文方法。同时AD-Slope方法采用子序列的斜率信息进行阈值判断，并未计算置信区间进行特征提取，所以其运行成本低于本文的运行成本。

从表1中R、P结果来看，本文与AD-Variance方法相比，查全率R以及查准率P分别提高了6.9%和4.3%，由于本文以子序列斜率的置信区间距离半径作为子序列的结构特征，更好地表示了子序列的特征变化，而AD-Variance方法采取子序列均值与方差作为子序列的特征，不能很好反映子序列的结构变化情况，因此，在R、P评价指标数值上低于本文的方法。与AD-Slope方法相比，本文方法的查全率R以及查准率P分别提高了46.3%和67.4%，本文采用子序列中的全部斜率信息进行特征提取，而AD-Slope方法仅采用子序列的第一个以及最后一个数据求解斜率，因而本文方法能够更好地保留了子序列中全部数据的形态信息，提高了子序列特征提取的准确性。从以上实验结果可以看出，本文方法的查准率R以及查全率P优于其余2种方法，但计算成本有所提升，考虑到本文提出方法具有较好的异常识别率，所提出的方法依旧具有较好的实用性。

2.2 工程数据验证

在本小节中，将所提出的检测方法应用于隧道掘进机(tunnel boring machine，TBM)实测数据的异常检测，以验证提出方法的工程可用性。该数据来源于国内某城市地铁隧道标段，隧道长度约2 km，直径6.4 m，采用推进速度作为检测对象，数据长度为1 800。

不同时间序列的子序列的特征数据分布具有差异性，因此本小节的最优阈值设为γ=0.04；滑动窗口长度设为l=7，所得实验结果如图5所示。可以看出，子序列特征曲线具有6个明显的异常峰值，即异常子序列。针对检测出来的子序列标号，形成如图6所示的异常子序列。从图6中可以看出，每一个异常子序列都包含了数据的异常值。

图5 子序列阈值判断

图6 检测出的异常子序列

针对这些异常子序列通过GG聚类算法实现异常值与正常值的归类与划分，表2中R、P为进行10次实验的平均值；D1，D2分别为查全率R以及查准率P的10次实验的方差，数值表示算法的波动情况。从表2中可以看出R、P都处于84%以上，且波动较小。针对隧道掘进机实测推进速度的异常检测结果，本文提出的算法具有较高的检测精度以及稳定性，表明该方法具有良好的工程可用性。

表2 推进速度异常值检测结果

3 结论

本文提出了一种基于滑动窗口的时间序列异常检测方法，通过斜率置信区间的方式解决了子序列特征难以提取的问题，采用滑动窗口方法和Gath-Geva聚类算法实现了异常值检测。仿真数据的实验结果表明，与以子序列方差信息和传统的斜率信息提取子序列特征的检测方法相比，本文提出的方法提高了检测精度。隧道掘进机实测数据的异常检测实验表明，提出的算法能够准确检测异常值信息，能够胜任工程数据的检测工作。