基于斐波那契数列的双通道绝对式时栅设计

瞿宝华，王阳阳，2，张天恒，梁 敏

(1.重庆理工大学机械检测技术与装备教育部工程中心，重庆 400054；2.重庆大学机械传动国家重点实验室，重庆 400044)

0 引言

随着工业自动化的不断深入发展，时栅测量技术日益广泛应用于控制和测量系统，测量技术的进步在一定程度上标志着一个国家工程质量的提高，对现代发展具有深远的意义[1]。绝对式轴角传感器由于自身的原理特性使其具备了位置信息可实现直接读取和断电保护等功能。目前的绝对式角位移传感器有光电式、磁电式和时栅。

光电式绝对式轴角编码器[2]原理为在圆周方向等量均分为一定量的区域。每个区域都只存在唯一区号代码，采用A/D模数转换器实现每个分区的中心位置精确定位。但是，由于光电式绝对式编码器需要对黑白条纹进行分别识别，在油污严重的状况下，很难实现对白色条纹的光学采样，从而降低了光电式编码器的精度等级。

绝对式磁电编码器[3-4]采用双通道形式，即在转动轴上安装同轴的粗机和精机，通过测量粗通道和精通道的转动角度反应真实转子位置角度。郝双晖[5]等提出一种新型多极磁电轴角编码器模型，基于双码道来实现角位移的绝对检测和高分辨率细分。Y.Deguchi[6]等提出通过改变磁极数由两极变为四极和传感器磁铁的偏心旋转，为绝对角检测提供了新的方法。但是，绝对式磁电编码器也存在缺点，比如在工况中产生脉冲式冲击载荷、结构尺寸大和硬件软件价格昂贵。

针对上述的两种绝对式编码器很难满足恶劣环境的需求，深化研究非调制式的低精度、低分辨力的增量式时栅传感器[7-8]，按照调制式的工作原理，将两组传感器按照一定的“精机+精机”方案组合成高精度的绝对式时栅位移传感器[9]。目前的绝对式时栅传感器的组合方式仍以经验方式建立，缺少理论依据的推导模型，科学性不强。

因此，绝对式时栅传感器的精度也会受到组合结构限制，如何确定“精机”的组合形式便成为了关键性问题。为了解决这个问题，文中提出了一种基于斐波那契数列的绝对式时栅位移传感器。斐波那契数列具有不断接近于黄金分割点的特性，因此按照斐波那契数列构造两组绝对式时栅位移传感器，其组合形式为“5X-3X”和“8X-5X”。然后对两组绝对式时栅位移传感器进行有限元仿真分析，通过数学分析软件进行分解。越趋近黄金分割点的绝对式时栅位移传感器误差越小，转角更接近于真实值。

1 绝对式时栅传感机理

根据时栅传感技术的理论，在研究对象中建立一套时空坐标转换体系，将空间位移量转换为测量离散时间脉冲信号，从而实现位移的准确测量。绝对式时栅传感器基于时栅传感技术，通过构造对极数互质的组合式传感器实现绝对式传感机理。

2组传感单元的输出信号为：

Em(t,x)=Acos(ωt-mμx),m=1,2,3,…

(1)

En(t,x)=Acos(ωt-nμx),n=1,2,3,…

(2)

式中：A为输出信号幅值；μ为角位移和直线位移转化因子；m和n分别为2组定子极对数。

2 斐波那契数列

斐波那契数列被认为是种具有非常严格的和谐性、比例性、艺术性的数字，是一种天然合理的最奇妙的形式比例，其中蕴藏着经典的协作组合[10]。

根据斐波那契数列的定义，如果某一数列满足：

F1=F2=1,Ft=Ft-1+Ft-2(t=3,4,5,…)

(3)

即1，1，2，3，5，8，13，21，34，55，89，144，…。我们将这一数列称为斐波那契数列。

其中，斐波那契数列表示为

(4)

斐波那契数列在工程上具有相当广泛的应用，石河子大学的吴雪飞[11]等采用黄金分割法对曲柄摇杆机构进行优化设计并确定最佳传动角。从结论可以明显看出黄金分割法优化设计与传统设计相比,既能提高机构的力传递性能,又能使机构的结构更加紧凑。长沙理工大学的李珊珊[12]在基于特征模型设计了滚珠丝杠传动系统的误差控制研究中，采用自适应黄金分割控制器可使系统具有一定的鲁棒性，并且对提高误差和机械传动精度提供可靠的理论依据。湖南大学的蒋增华[13]使用黄金分割法对阈值的设置进行了优化。与传统方法相比较，弥补了信号特征值阈值在设置上存在的缺陷。

斐波那契数列在工程应用上具有很深远的研究意义，其在结构设计和传动精度上，甚至在测量精度上都有研究价值。文中采用斐波那契数列方法对模型组合优化，从而实现高精度绝对位置的测量。

3 基于斐波那契数列的绝对式时栅

3.1 模型设计及传感机理

为了构建基于斐波那契数列的绝对式优化模型，其机械零件采用表1的同一套模型设计参数。

表1 模型设计参数表 mm

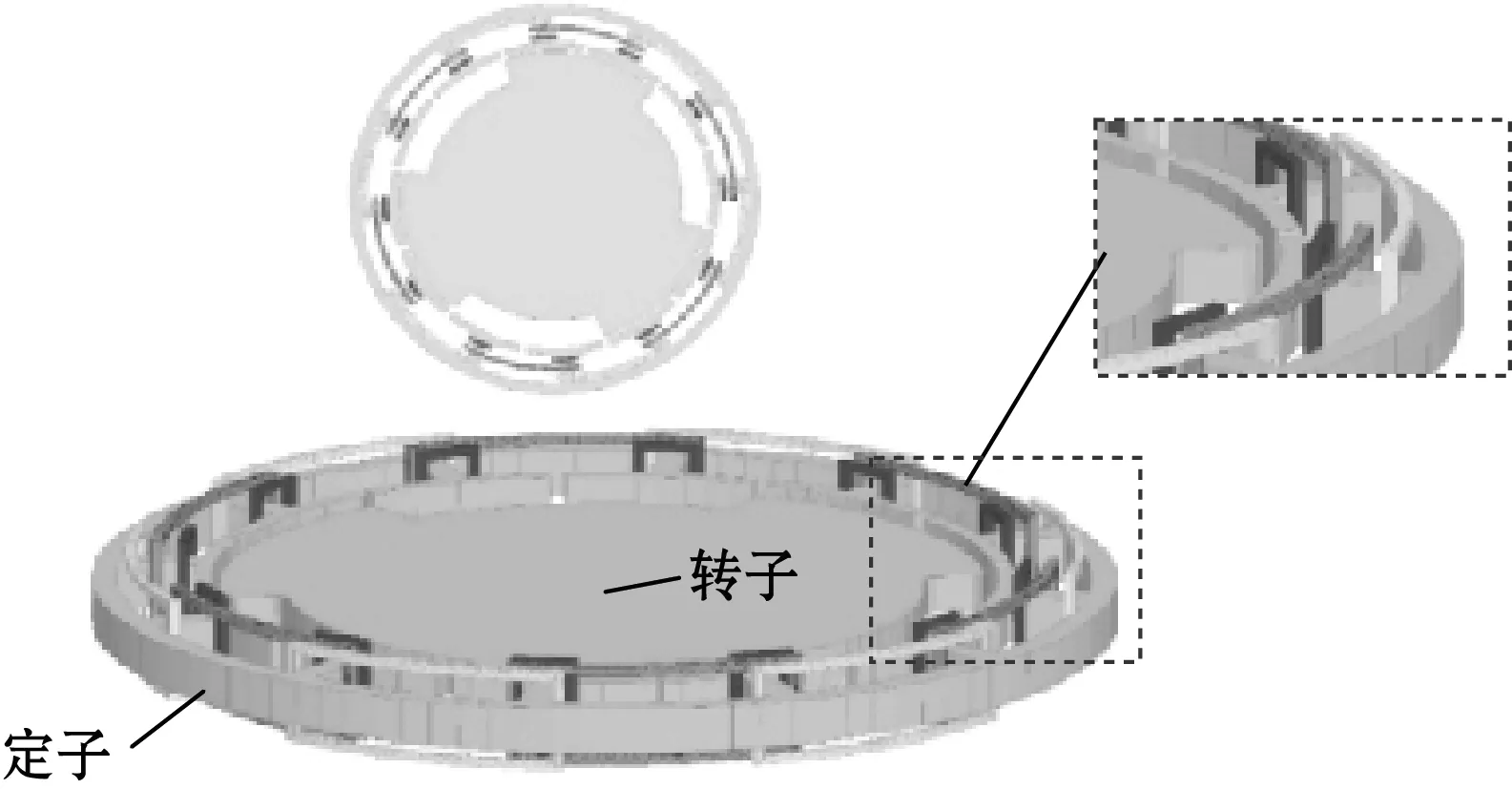
图1 3X仿真结构模型

图2 5X仿真结构模型

图3 8X仿真结构模型

仅通过仿真模型的建立不能够满足时栅传感原理，因此，进一步实现时间正交的信号，绕线方式是构建时间正交重要技术方法。线圈绕线方式如图4所示，三行线圈分别为正弦、余弦和感应绕组，每行线圈通过串联构建。

图4 激励和感应绕线方式

为了建立时间正交的电信号，将Vmaxsin(ωt)和Vmaxcos(ωt)通入2组激励线圈中，根据与之相对应的m和n对极分别可以得到2驻波信号公式：

(5)

(6)

式中：Wm和Wn分别为m、n对极的极距；x为相对应的位移量。

将2组绝对式时栅传感器感应得到的驻波信号经过叠加原理，得到2列感应行波电信号：

(7)

(8)

式中：φm和φn分别为m、n对极的初相位。

3.2 模型仿真及数据分析

将定转子齿数比为4：1的时栅传感器三维模型分别导入有限元仿真软件。充分考虑到仿真的参数对仿真结果的影响，线圈既不能紧贴定子齿槽，又不能太远离定子齿槽，否则定子的磁场将被极大的削减。模型的属性参数见表2。

表2 模型仿真参数表

建立如图5和图6所示的对比性仿真实验。传感器的驻波信号通过信号调制，最终构建时间测量位移的脉冲波形。由于两 “精机”具有不同的对极数，采集到不同精度的脉冲，即“精+精”组合的绝对测量系统。因此，在满足精度的要求下实现绝对位置测量。

图5 5X-3X组合绝对式传感器理论模型

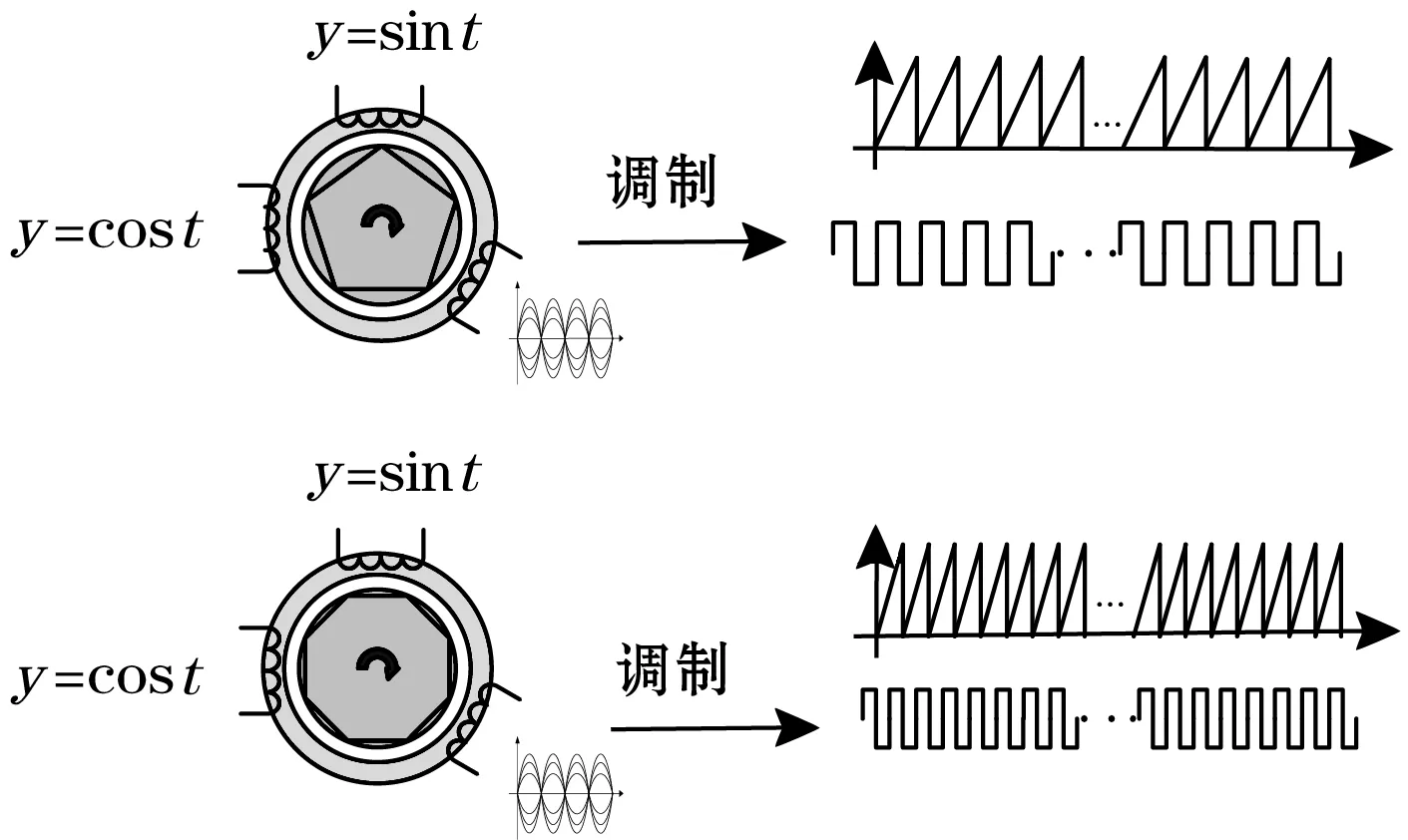
图6 8X-5X组合绝对式传感器理论模型

通过上一节的建立结构模型和仿真机理，得要3组电行波信号，如图7、图8、图9所示。

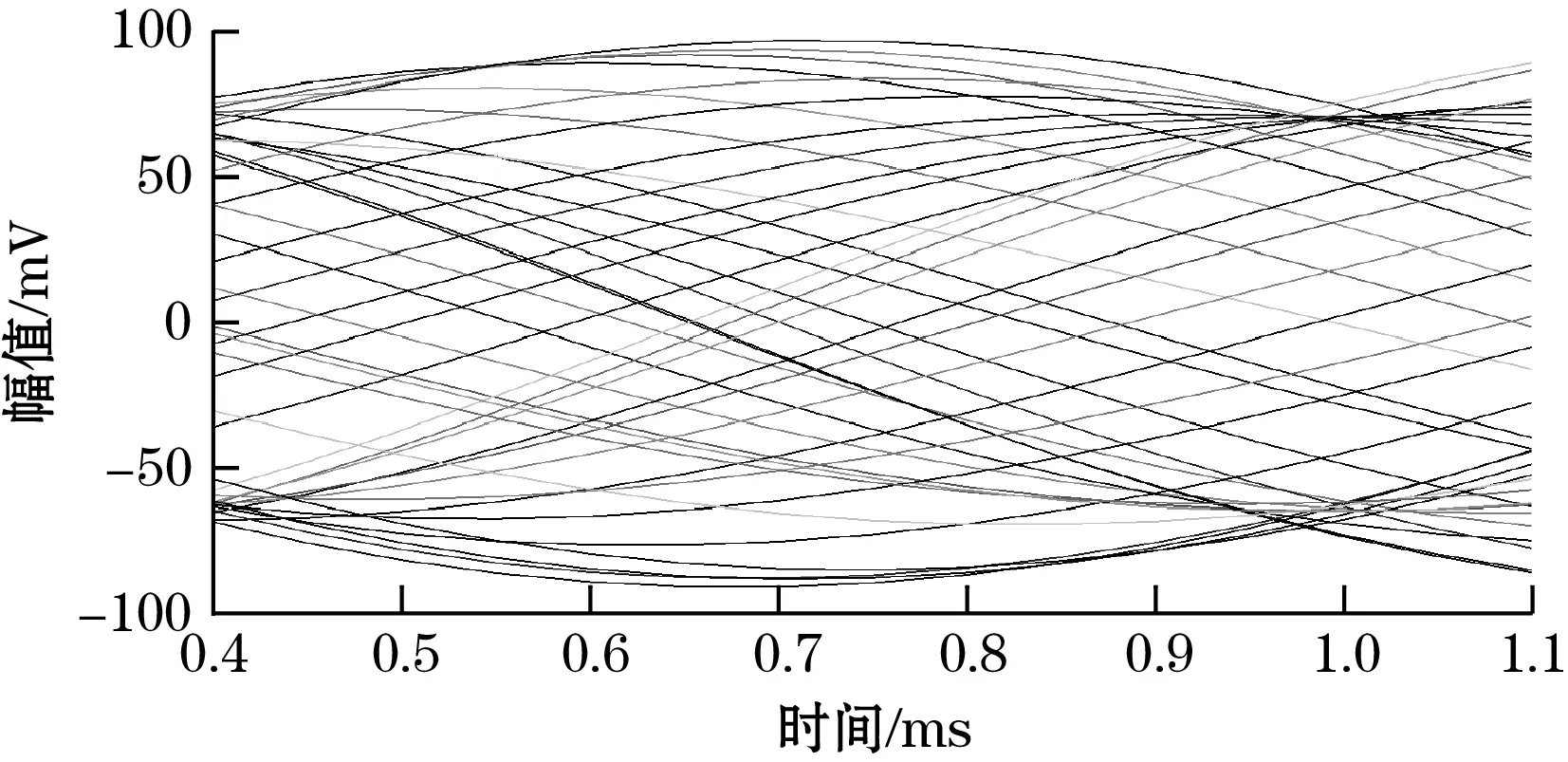
图7 3X感应线圈的输出电动势

图8 5X感应线圈的输出电动势

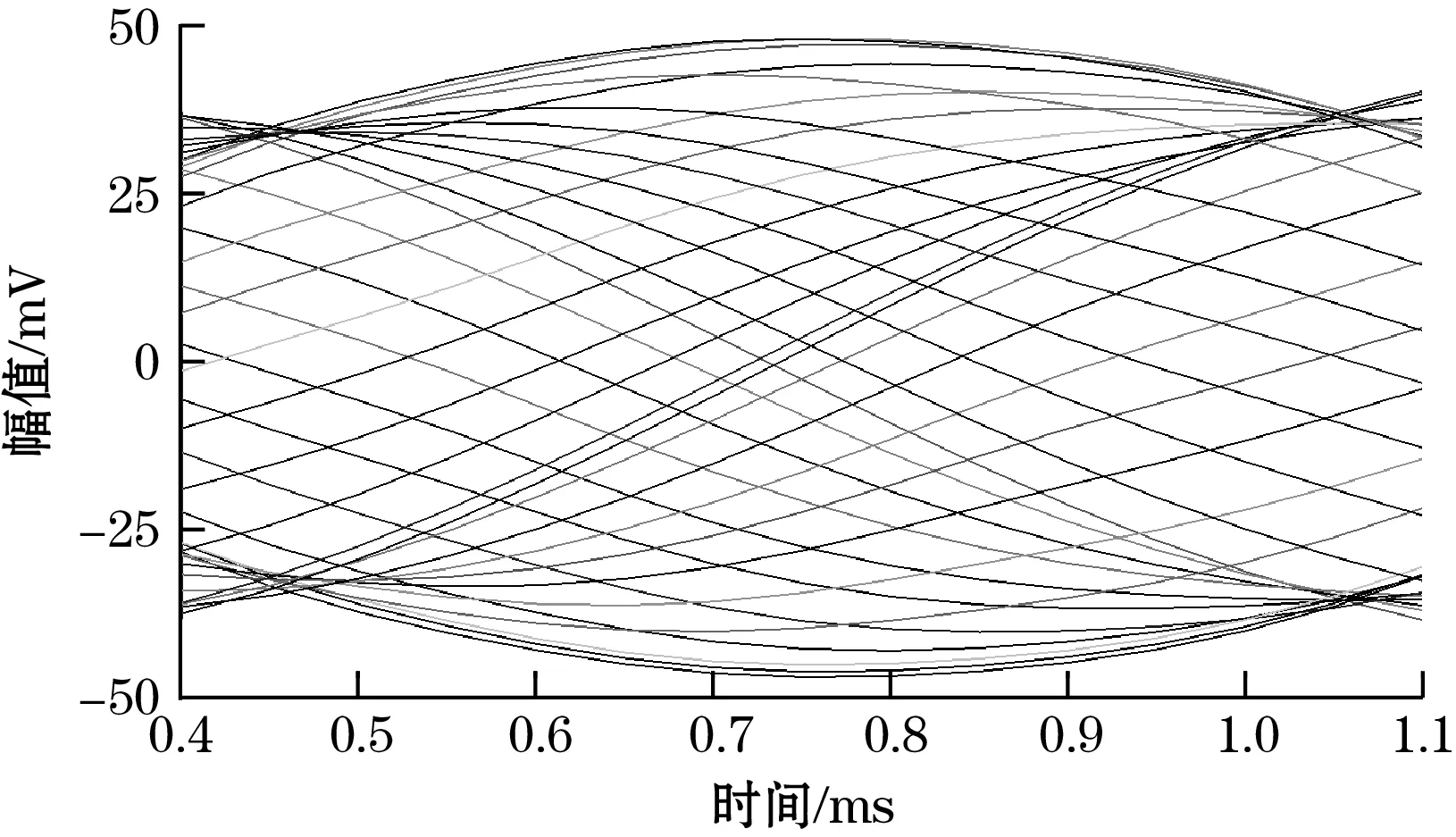
图9 8X感应线圈的输出电动势

经过仿真软件采集到时空正交的电信号。通过数学分析工具软件，将2组绝对式时栅传感所得到的基波相位信息经过计算绘制出组合测量的误差曲线。如图10、图11所示。

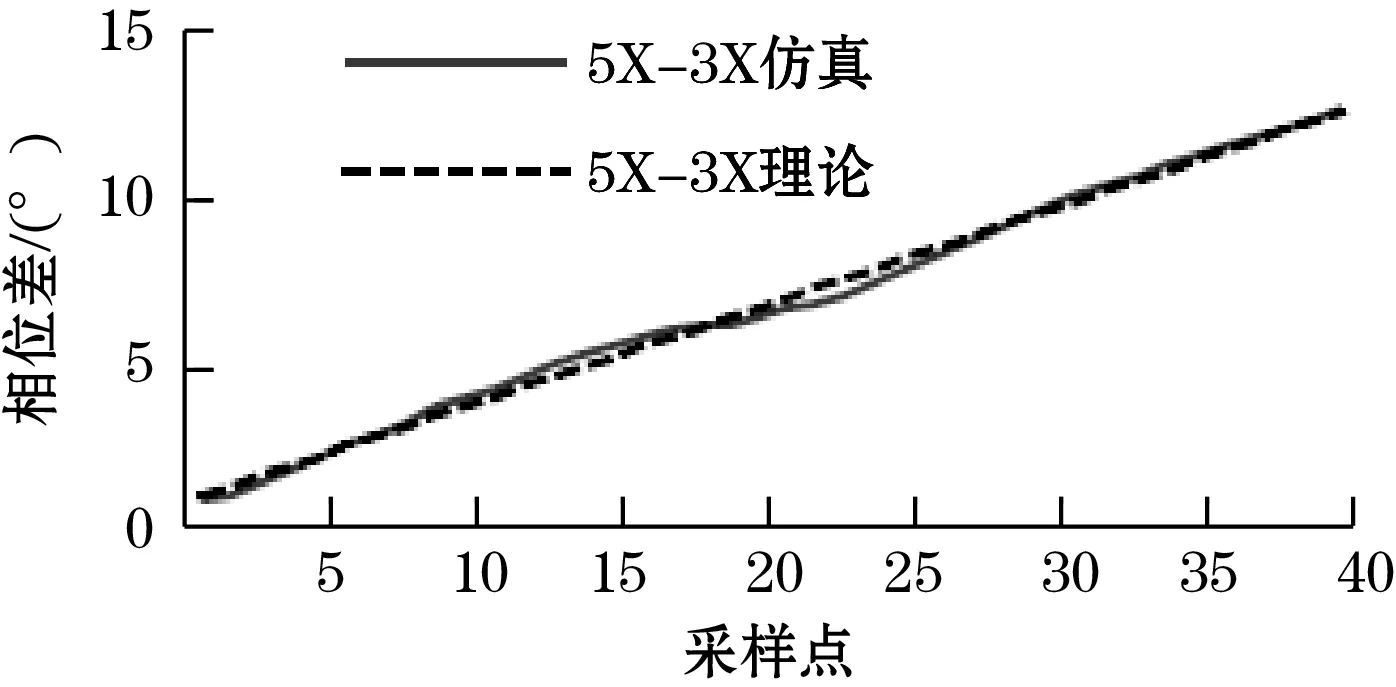
图10 5X-3X绝对位置测量误差

图11 8X-5X绝对位置测量误差

Error=|ysimulation-ytheory|

(9)

式(9)即为仿真相位差与理论相位差的真实误差值。

根据式(9)，可以计算出max{Error}。其中，

max{Error5X-3X}=1.402 136°

max{Error8X-5X}=0.319 324°

通过2组绝对式传感位置测量误差表明，“8X-5X”组合的“精机+精机”组合式传感器误差精度得到了一定的提高。根据斐波那契数列特征，数列越往后，参数结构越趋于最优解。因此，“8X-5X”绝对式传感器参数优化符合斐波那契数列特征。

4 仿真实验验证

为了进一步证实本论文所提出来的满足黄金分割点的“精机+精机”绝对时栅传感器具有组合优化的依据。将采用“13X-8X”组合的绝对式时栅传感器，通过仿真软件仿真、数据分析处理，其结果如图12、图13、图14所示。

图12 13X仿真结构模型

图13 13X感应线圈的输出电动势

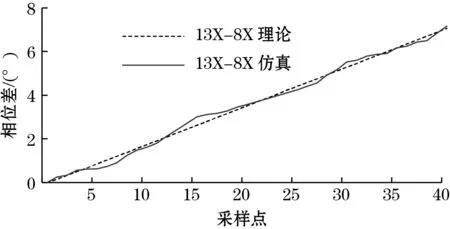
图14 13X-8X绝对位置测量误差

根据式(9)，max{Error13X-8X}=0.283 686°。

max{Error13X-8X}

即，相位误差满足黄金分割优化特性。

5 结论

绝对式时栅位移传感器不仅能实现位置信息直接测量和断电保护，还具有优秀的抗干扰能力。文中通过引入斐波那契数列旨在寻找一种可以为双通道绝对式时栅的结构设计提供一种准则和有效的理论途径实现传感器的结构优化与精度提升。文中通过开展一系列仿真实验，仿真结果表明基于斐波那契数列的组合方式对绝对式时栅传感器的结构设计具有一定的成效，通过几组对比论证进一步验证了斐波那契数列对结构优化的指导意义。