复合顶板锚杆力学特征分析

王建伟，展勤建

(1.瓦斯灾害监控与应急技术国家重点实验室，重庆 400037；2.中煤科工集团重庆研究院有限公司，重庆 400037；3.太原理工大学，山西 太原 030024；4.广东石油化工学院，广东 茂名 525000)

0 引 言

由于各分层间物理性能差异较大，层间黏结力较低[1-3]，相对于单一岩层，复合顶板内锚杆的力学特征存在独特的复杂性。尽管国内外学者针对复合顶板的锚固支护技术进行了深入的研讨，相关理论已取得了长足有效的发展，为巷道围岩的稳定控制做出了一定贡献，涉及的研究手段及治理方法亦不失为有效的技术途径[4-5]。然而，由于研究焦点主要集中于复合顶板巷道围岩的稳定性控制和锚杆支护系统整体作用效果的探讨：或为归纳分类复合岩层的破坏机理及形式，并提出相应的巷道围岩控制措施[6-9]，或为突出锚杆支护系统对软硬相间岩层的加固效果[5,10-12]，但未能形成通识的基础理论。

复合顶板巷道的稳定控制势必成为后续煤炭开采过程中主要的技术难题之一。随着浅部优质资源的日益枯竭，由于技术瓶颈的制约和综合机械化高强度开采，加速开采岩性劣化及地质结构复杂程度加剧的深部资源的进程已日益凸显[13-14]。加之与沉积岩形成有关的煤系地层对巷道层位的影响，复合顶板成为煤炭资源开采过程中常见的顶板类型。然而，由于缺乏必要的针对性研究，复合顶板的锚杆支护体系设计通常基于经验主义和感知性能，加之经济因素的制约，往往使得复合顶板的锚固支护系统不尽合理，甚至承受由于顶板事故的发生所带来的问题[15]。因此，有必要针对复合顶板巷道合理支护技术开展进一步系统深入的研究。其中，探寻复合顶板内锚杆合理的力学模型，进而开展锚杆力学特征分析显得尤为重要。

纵观已有研究，当前复合顶板巷道的锚杆支护技术仍然处于起步阶段，复合顶板内锚杆力学特征分析的研究更鲜见于文献。本文基于一定的条件假设，借鉴桩基础平衡理论的研究成果，建立了复合顶板内锚杆力学模型，通过理论推导、案例的MATLAB解析计算及FLAC3D模拟对比分析，验证了复合顶板内锚杆力学模型的正确性。在此基础上，进行了复合顶板锚杆的轴力与胶结面上切应力分布形态分析。相应研究手段及结论为复合顶板内锚杆的力学特征分析及支护设计提供一种有效的新途径。

1 复合顶板锚固体系的本构方程

1.1 条件假设及模型的建立

为了建立复合顶板内锚杆的力学模型，将锚杆侧岩体阻力以周-边弹簧代替，弹簧的刚度系数为ki=2.75Gi/(πD)，锚杆端部岩体阻力以端部弹簧代替，刚度系数为k0=8G1/[πD(1-μ1)]。其中，Gi为第i层围岩的剪切模量，如G1为锚固端部所在岩层的剪切模量，μ1为锚固端部所在岩层的泊松比，D为锚固体直径。由此建立的复合顶板锚固系统的轴向力学模型如图1所示。

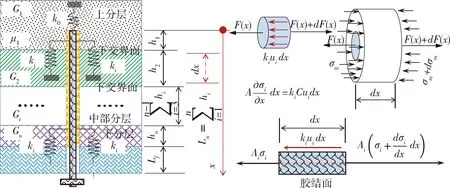
图1 锚固系统轴向力学模型

在忽略次要因素的基础上提出以下假设条件。①锚杆为连续弹性的均质圆截面杆体，锚固体在轴向变形时满足平面设计；②虽已有研究表明复合顶板为正交各向异性或各向异性体，但由于锚杆力学特征主要表现在轴向方向上，其与复合顶板岩层的层位关系存在一定的特殊性，本文认为锚固剂及复合顶板锚固段内各分层仍为各向同性的均质弹性体；③锚固段内岩体处于完全线弹性状态，锚杆与围岩之间的相互作用采用线弹性弹簧加以实现；④不考虑围岩变形产生的附加荷载等其他因素对锚杆受力特征的影响；⑤忽略锚杆在轴向拉伸或压缩时横截面的改变量以及围岩与胶结面滑移所带来的损伤效应；⑥不考虑实际工程中软弱结构面、节理裂隙、断层结构以及岩层交界面处的离层等因素；⑦锚杆-锚固剂-围岩黏结良好，即锚杆与围岩满足变形协调的条件。

截取长度为dx的锚固微元体为研究对象，如图1所示，由平衡条件可得锚固微元体轴向平衡方程，见式(1)。

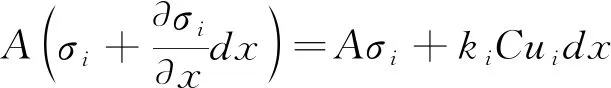
(1)

式中：A为锚杆横截面积；C为锚杆圆截面周长；ui为锚杆轴向位移函数；σi为锚杆横截面上的正应力；i为锚固段内岩层的编号，i=1，2，…，n。

由胡克定律可得式(2)。

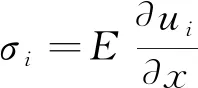
(2)

将式(2)代入式(1)可得式(3)。

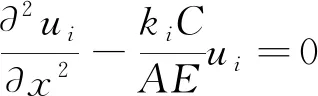
(3)

1.2 锚固段内锚杆位移函数

锚固微元体取于第一层岩层内，此时有式(4)。

(4)

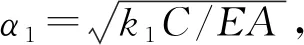
(5)

由此，式(5)的解为式(6)。

u1=C1eα1x+C2e-α1x

(6)

同理可得式(7)。

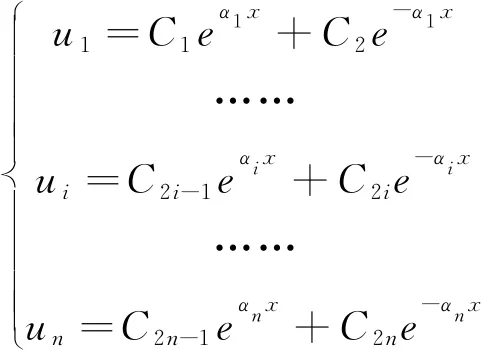
(7)

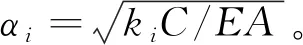
1.3 自由段内锚杆位移函数

锚固微元体取于自由段内时，此时有式(8)。

(8)

式中，σ*为锚杆横截面上的正应力，由此可得式(9)。

(9)

式中，u*为自由段内锚杆轴向位移函数。因此，自由段内锚杆位移函数的解为式(10)。

u*=C2n+1x+C2n+2

(10)

1.4 边界条件和连续条件

设巷道支护平衡时，锚杆根部轴力为F，则锚杆锚固系统对应的边界条件为式(11)。

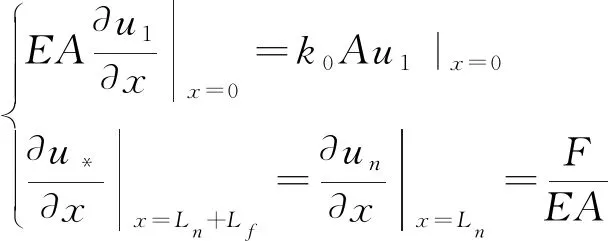
(11)

为了保证锚杆的完整性，各段间还应满足位移的连续条件，见式(12)。

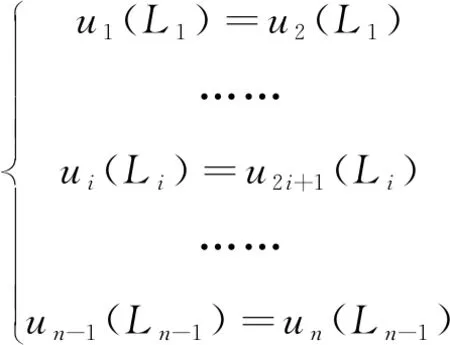
(12)

与此同时，各段间还应满足锚杆轴力连续条件见式(13)。

(13)

1.5 常数项的求解

观察式(7)可知，若要完整获得锚杆位移函数的解，则必须完成常数项求解过程。结合上述公式，为说明常数项的存在和唯一性，本文给出了n=4时锚杆位移函数的常数项求解过程及结果。结合上述边界条件和连续条件可得独立方程见式(14)。

(14)

由式(14)可得相应常系数项见式(15)。

式中：

λ1=(1+α3/α4)[(1+α1/α2)(1+α2/α3)eβ1+

(1-α1/α2)(1-α2/α3)eβ2]+

“从政经验型”类似宋元时期的“概论体”，是宋元以来官箴书的主流类型与模式。所谓“从政经验”，即作者直接表达或论述从政者在到任离职、人际关系、行政事务等方面所应遵循的原则、秉持的官德、注意的事项，或办事的方法技巧等，以达到对官员进行劝诫与教导之目的。可以说，宋元及明代中前期大多数官箴书基本上都属于此种类型。晚明官箴书依旧继承了宋元以来的这种书写方式。如佘自强的《治谱》直接论述或表达官吏在从政中应注意的事项及施政的方法技巧，这就是宋元官箴书的主流模式。

(1-α3/α4)[(1+α1/α2)(1-α2/α3)eβ5+

(1-α1/α2)(1+α2/α3)eβ6]

λ2=(1+α3/α4)[(1-α1/α2)(1+α2/α3)eβ3+

(1+α1/α2)(1-α2/α3)eβ4]+

(1-α3/α4)[(1-α1/α2)(1-α2/α3)eβ7+

(1+α1/α2)(1+α2/α3)eβ8]

λ3=e2α4L3{(1-α3/α4)[(1+α1/α2)(1+α2/α3)eβ1+

(1-α1/α2)(1-α2/α3)eβ2]+

(1-α1/α2)(1+α2/α3)eβ6]}

λ4={(1-α3-α4)[(1-α1/α2)(1+α2/α3)eβ3+

(1+α1/α2)(1-α2/α3)eβ4]+

(1+α3/α4)[(1-α1/α2)(1-α2/α3)eβ7+

(1+α1/α2)(1+α2/α3)eβ8]}e2α4L3

其中：

结合上述求解结果及理论分析可知，复合顶板内锚杆的位移函数主要由下列参量控制：α1，…，αi，…，αn，(i=1，2，…，n)。

2 算例验证与分析

为了验证上述力学模型的正确性，结合工程实际，选取一算例，矩形煤巷埋深420 m，巷道宽4.0 m，高3.0 m，巷道顶板为复合顶板。锚杆支护间排距为1.0 m×1.0 m，锚杆选取直径为25 mm的左旋无纵筋螺纹钢锚杆，锚杆弹性模量为200 GPa。巷道顶板自上而下的岩层分别为：①细砂岩，剪切模量G1=7.6 GPa，泊松比μ=0.20，岩层厚度为6.0 m，L1=1.0 m；②砂岩，剪切模量G2=3.80 GPa，岩层厚度为1.0 m；③砂质泥岩，剪切模量G3=1.75 GPa，岩层厚度为1.0 m；④泥岩，剪切模量G4=0.90 GPa，岩层厚度为1.0 m。

本文主要通过FLAC3D模拟监测数据和理论计算数据的对比分析加以验证。模拟过程中不仅对巷道两侧的煤层(单一岩层)内锚杆不同截面位置的位移进行了监测，而且对顶板(复合岩层)内锚杆不同截面位置的位移进行了监测。FlAC3D模型及巷道锚杆支护工况如图2所示，位移监测结果和理论计算结果如图3所示。

图2 FlAC3D建模和支护工况示意图

由图3可知，模拟监测和理论计算结果呈现出相同的位移分布形态。其中，巷道两侧煤体内锚杆位移误差仅介于1.66×10-4～4.0×10-2mm，误差百分比介于0.01%～9.17%。而巷道顶板内锚杆位移误差范围仅介于0～5.0×10-2mm，误差百分比介于0%～9.83%。由此可见，无论是煤体(单一岩层)内的锚杆，或是复合顶板内的锚杆，数值模拟与理论计算的差异均较小，基本控制在10%以内。这表明采用上述理论模型进行锚杆力学特征分析是可行的，相应理论推导过程及计算结果是可靠的。

图3 理论计算和数值模拟的位移曲线

3 锚杆轴力与切应力分布规律

结合上述理论推导过程可知，复合顶板内锚杆轴力计算公式见式(16)。

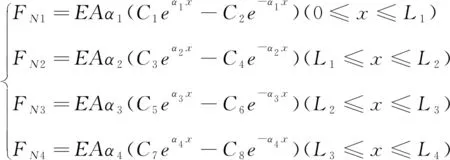
(16)

同时，由于dFi=kiCuidx=τiCdx,则有式(17)。

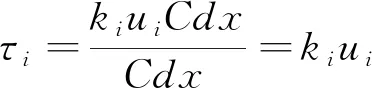
(17)

结合上述理论分析，在设定锚杆锚固段长度为Ln=4.0 m，将锚固段内复合岩层数量设定为n=4，通过设置软硬相间岩层的不同高度，进行了锚固段内任意截面位置锚杆轴力的理论计算可知，虽然锚杆轴力的解析结果主要由α1，…，αi，…，αn，(i=1，2，…，n)控制，由于复合岩层厚度一般较小，各分层厚度在一定范围内的变化，似乎对于锚杆轴力的分布形态影响甚微。结合工程实际，本文仅通过复合顶板内各分层剪切模量的梯度性变化，进行了锚杆轴力、胶结面切应力分布形态的考察和随剪切模量的动态响应机制分析。

3.1 复合顶板锚杆轴力分布规律

设巷道复合顶板内锚固段内自上而下岩层剪切模量分别为G1、G2、G3、G4，自上而下的岩层厚度分别为h1=h2=h3=h4=1.0 m，锚杆端部所处岩体泊松比设定为μ1=0.20。 需要说明的是，为进行剪切模量梯度性变化的岩层，其剪切模量均为0.2 GPa，锚杆根部轴力F=100 kN，锚杆轴力分布形态如图4所示。

图4 不同剪切模量时锚杆轴力分布形态

1) 结合上述理论分析，复合顶板的各分层内锚杆轴力的分布形式为分段的指数函数，分段形式主要受分层间剪切模量的差异化影响，指数函数的分段边界为各分层的上下交界面位置。这将导致锚杆轴力的分布均在各分层的交界面位置出现拐点。

2) 分层剪切模量的梯度性变化，将影响锚固段内锚杆轴力的整体分布形态。上下分层(图4)剪切模量的梯度性变化，将导致锚固段内锚杆轴力的分布形态呈现相反的响应特征。上分层剪切模量增大，则锚固段内锚杆轴力整体增大；下分层剪切模量增大，则锚固段内锚杆轴力整体减小。

3) 而关于中部分层(图4)剪切模量的梯度性变化，锚杆轴力分布形态呈现相同的响应特征，值得注意的是，发生梯度性变化的分层将锚固段锚杆分为两个区段，区段的分界点位于本分层内，为了说明问题，划定分界点上方为上区段，下方为下区段。随着某分层剪切模量的增大，上区段锚杆轴力逐渐减小，而下区段锚杆轴力逐渐增大，且相对于该分层上下交界面距离愈小，关于剪切模量的响应程度愈强烈。

4) 锚杆轴力关于不同分层的剪切模量的梯度性变化亦有所不同，相对于下分层距离愈小，随着分层剪切模量的增大，锚杆轴力的响应程度愈强烈，在分层厚度一致的情况下，锚杆轴力关于下分层剪切模量的响应程度最为强烈，增幅及增量的峰值出现在交界面位置。

3.2 胶结面上切应力分布规律

为了说明问题，在3.1部分锚杆轴力计算时选定的分层剪切模量基础上，进行了锚固段锚杆胶结面上切应力计算，结合分层剪切模量的梯度性变化，不同剪切模量胶界面上切应力分布形态如图5所示。

图5 不同剪切模量时切应力分布形态

1) 由于理论模型基于锚杆轴向平衡理论，随着各分层剪切模量的梯度性变化，锚杆胶结面上切应力分布形态呈现出与锚杆轴力相对应的响应特征。锚杆胶结面上切应力的分布形式亦为分段的指数函数，函数的分段边界同为各分层的上下交界面位置；同时，由于支护荷载一定，锚固段内锚杆轴力增大的同时，胶结面上的切应力减小。不同之处在于，轴力出现拐点位置，切应力产生突变。

2) 胶结面上切应力峰值主要出现在两个位置，其一为锚杆自由段与锚固段的交界处附近(端锚形式)，或是锚杆根部(全锚形式)，这将会在锚固段内各分层剪切模量差异化较小时出现；其二为锚固段内剪切模量相对较大的分层交界面位置，这将会在锚固段内各分层剪切模量差异化较大时出现。

3) 与锚杆轴力的响应特征有所不同的是，分层剪切模量的增大将导致其他分层内锚杆胶界面上切应力减小，相对于该分层的距离愈小，响应程度愈强烈。而该分层内锚杆胶结面上的切应力全区段增大，且沿上分界面至下分界面方向上，切应力的增量及增幅逐渐增大。

4 结 论

1) 由于分层间剪切模量的差异化，复合顶板内锚杆位移、轴力及胶结面切应力分布形式均为分段的指数函数，函数的主要控制量分别为α1，α2，…，αn。指数函数的分段边界为各分层的上下交界面位置。锚杆轴力在上下交界面位置出现拐点，而胶结面上切应力则在此出现突变。

2) 分层剪切模量对锚杆轴力的影响机制方面。上下分层剪切模量的梯度性变化，将导致锚固段内锚杆轴力分布形态呈现相反的响应特征，上分层剪切模量增大，则锚固段内锚杆轴力整体增大；下分层剪切模量增大，则锚固段内锚杆轴力整体减小。而中部分层剪切模量梯度性变化时，将锚固段锚杆分为两个区段，分界点位于该分层内，随着剪切模量的增大，上区段锚杆轴力逐渐减小，而下区段逐渐增大。相对该分层上下交界面位置愈小，关于剪切模量的响应程度越为强烈。

3) 锚杆胶结面上切应力峰值主要出现在两个位置，其一为锚杆自由段与锚固段的交界附近(端锚形式，)或是锚杆根部(全锚形式)，这将会在锚固段内各分层剪切模量差异化较小时出现；其二为剪切模量相对较大分层的下交界面位置，这将会在复合顶板内各分层剪切模量差异化较大时出现。

4) 分层剪切模量的增大将导致其他分层内胶结面上切应力减小，相对于该分层距离愈大，减小的幅值及幅度愈小；而该分层内胶结面上切应力增大，沿上分界面至下分界面方向，增量及增幅逐渐增大。