基于蝙蝠算法的概率积分预计参数反演方法

李 忠，王 磊，滕超群，李世保，黄金中

(安徽理工大学空间信息与测绘工程学院，安徽 淮南 232001)

我国作为世界能源生产大国和消费大国，煤炭资源丰富，储量居世界前列。作为三大化石燃料之一，煤是重要的能源，也是冶金、化学工业的重要原料，然而随着大量煤炭资源的开采，常常引起开采区地层发生错动、地表下沉等一系列问题，对矿区周围村庄村民的生产生活产生了极大影响，因此开采沉陷预测的准确性显得尤其重要[1]。概率积分法(probability integral method，PIM)预计模型是我国在开采沉陷中应用最广泛的方法[2]，其参数反演过程经历了线性近似法[3]、正交实验法、模矢法[4]、人工神经网络法[5]、智能优化算法(如遗传算法[6])等。常见参数反演方法主要特点见表1。

表1 常见参数反演方法对比

目前遗传算法在参数反演方面得到广泛应用，国内很多学者利用智能优化算法进行概率积分法参数反演，如利用果蝇算法[7]、粒子群算法[8]、狼群算法[9]、混合蛙跳算法[10]等进行概率积分法模型参数反演，为概率积分法参数求解提供了众多新的途径。2010年YANG[11]提出了一种基于迭代优化技术的新型群体智能优化算法——蝙蝠算法(bat algorithm，BA)，因模型简单易懂、参数少、求参稳定性高、收敛速度快等优点，现已在工程优化[12]、模型识别[13]等问题中得到了广泛的应用，然而蝙蝠算法作为智能优化算法领域新的研究热点，在概率积分模型参数反演的问题上却鲜少有结合应用。

因此，本文将BA引入概率积分模型参数反演中，构建了基于蝙蝠算法的概率积分预计参数反演模型，并通过模拟实验验证蝙蝠算法反演模型的正确性，随后将其应用于淮南市某煤矿1414工作面[14]的预计参数反演中，求得该工作面开采后沉降稳定时的预计参数。

1 模型构建

1.1 PIM基础理论

按概率积分法原理，单元开采引起的地表任一点的下沉值计算见式(1)～式(4)。

W(x,y)=

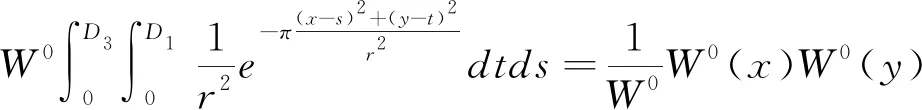
(1)

W0=mqcosα

(2)

W0(x)=

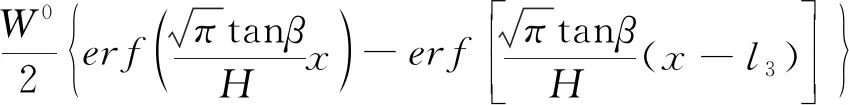
(3)

W0(y)=

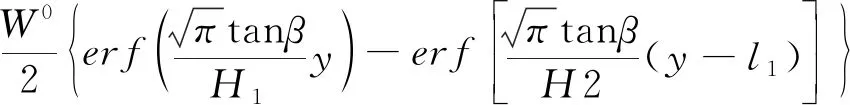
(4)

式中：m为工作面平均开采厚度；q为下沉系数；α为工作面倾角；tanβ为主要影响角正切；H为走向主断面采深；H1、H2分别为工作面上边界采深、下边界采深；D3、D1分别为开采工作面走向长度、倾向长度；l3、l1分别为工作面走向计算长度、倾向计算长度。

同理，单元开采引起的地表任一点沿φ方向的水平移动值计算见式(5)～式(7)。

U(x,y,φ)=

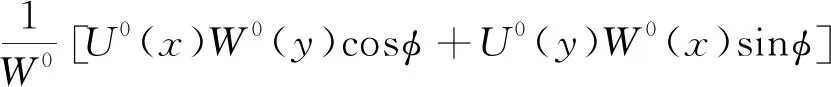
(5)

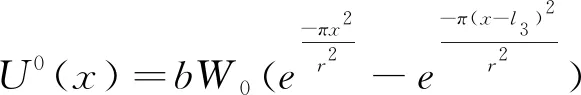
(6)

(7)

式中：b为水平移动系数；φ为x轴的正向逆时针到指定方向的角值；r1、r2为下山主要影响半径和上山主要影响半径。

1.2 BA基础理论

蝙蝠可以在夜间自由飞翔并准确无误地捕捉食物，主要是依靠它们的喉头发出超声脉冲进行回声定位，在蝙蝠算法中，为了模拟蝙蝠捕食猎物、避免障碍随机搜索过程，做出三种近似理想化规则假设。

1) 在设定的种群里，所有的蝙蝠获取方法和距离的方法都是回声定位。

2) 蝙蝠i在某一位置X时以Vi的速度进行飞行，其具有固定的频率fmin，并且可以利用自身与目标的距离自动调整脉冲响度A和波长λ。

3) 设定脉冲响度A是一个由最大值A0变化到固定最小值Amin的过程，具体的A0和Amin的值由所解决的问题而调整。

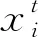
fi=fmin+(fmax-fmin)×β

(8)

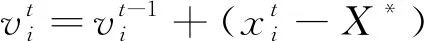
(9)

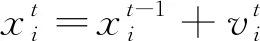
(10)

式中：fi为蝙蝠发出声波的频率，其变化在[fmin，fmax]的区间范围内，在具体问题中根据问题的需要设置对应的频率变化范围；β为属于[0,1]的随机向量；X*为当前群体中局部最优解位置。

在进行局部搜索时，若生成了一个局部新解，则新的局部解将会采用的生成方式为随机游走，新的局部解生成规则为式(11)。

xnew=xold+ε×At

(11)

式中：ε为一个[-1,1]范围内的随机数；At为整个群体里同一代的平均响度。

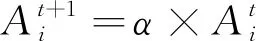
(12)

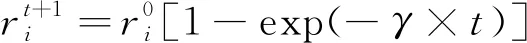
(13)

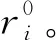
1.3 BA-PIM模型构建

假设在工作面任意一点(x,y)进行开采，Wxy为开采点的实际下沉值，Uxy为开采点的实际水平移动值，将BA反演的PIM预计参数带入到PIM模型中，得到开采点的预计下沉值及水平移动值Wxy预和Uxy预,并构造以开采点的实测值与预计值之差的绝对值累计和最小为标准的适应度函数见式(14)。

S=sum[abs(Wxy-Wxy预)+abs(Uxy-Uxy预)]

(14)

令X*=[q，tanβ，b，θ，S1，S2，S3，S4]为BA算法中最优蝙蝠位置的解空间，将适应度函数值最小作为判断每一次蝙蝠最优位置的标准。在每一次迭代的过程中蝙蝠群体根据调整脉冲响度和频率来搜寻并捕获猎物，当满足终止条件后，输出最优的蝙蝠位置X*。其算法模型的具体步骤如下所述。

1) 设置蝙蝠群体的数量N，最大迭代次数T，蝙蝠声波频率范围值[fmin，fmax]，蝙蝠i的初始速度V、脉冲响度衰减系数α及脉冲频度增强系数γ的大小、初始脉冲大小；约束PIM八参数的波动范围，读取观测点的实际下沉值Wxy和水平移动值Uxy。

2) 机初始化蝙蝠Xi的位置并利用式(14)中的适应度函数输出最优的蝙蝠位置并储存。 由式(8)～式(10)更新蝙蝠i此时的频率、速度及位置。

3) 生成一个[0,1]随机数Rand1，如果Rand1大于当前最优蝙蝠发出的脉冲频率ri则根据式(11)进行局部新解搜寻并储存当前新解，否则继续利用式(10)更新蝙蝠的位置。

4) 继续生成一个[0,1]随机数Rand2，如果Rand2小于当前最优蝙蝠发出的脉冲响度Ai，并且此时适应度函数生成的解优于步骤3)的解，则接受此时蝙蝠的最新位置解，然后根据式(12)和式(13)更新蝙蝠i的脉冲响度和频率。

5) 对种群中所有蝙蝠个体的适应度值进行排序，输出当前最佳位置蝙蝠。

6) 转到步骤2)～步骤5)，直到达到迭代次数，输出全局最优蝙蝠位置X*。

基于BA的概率积分预计参数反演方法程序流程图如图1所示。

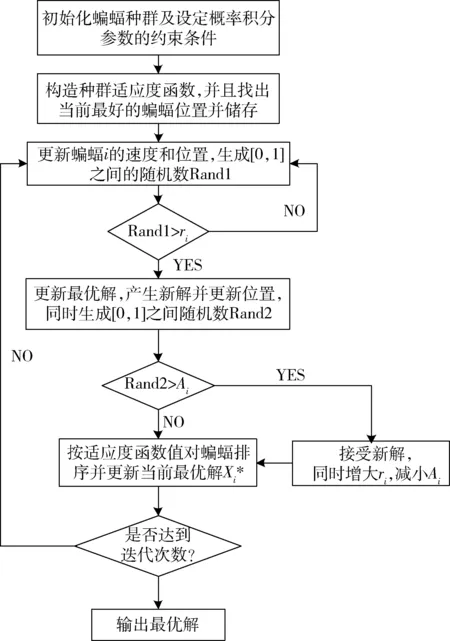
图1 BA反演PIM参数流程图

2 模拟实验

2.1 工作面概述

为了验证BA算法应用于PIM求参的准确性，故建立如下模拟工作面：矩形工作面走向长度D3=600 m，倾向长度D1=300 m，煤层开采厚度m=3.6 m，煤层倾角α=6°，平均开采深度H=400 m，管理顶板的方法采用全部垮落法。此次模拟工作面实验走向主断面上相邻两个观测站之间间隔30 m，倾向主断面观测站布设方式同走向。假定模拟工作面PIM预计参数分别为：下沉系数q=0.9，主要影响正切角tanβ=2.1，水平移动系数b=0.35，开采影响传播角θ=87°，拐点偏移距：S1=S2=50 m、S3=S4=50 m。本模拟工作面设计图如图2所示。

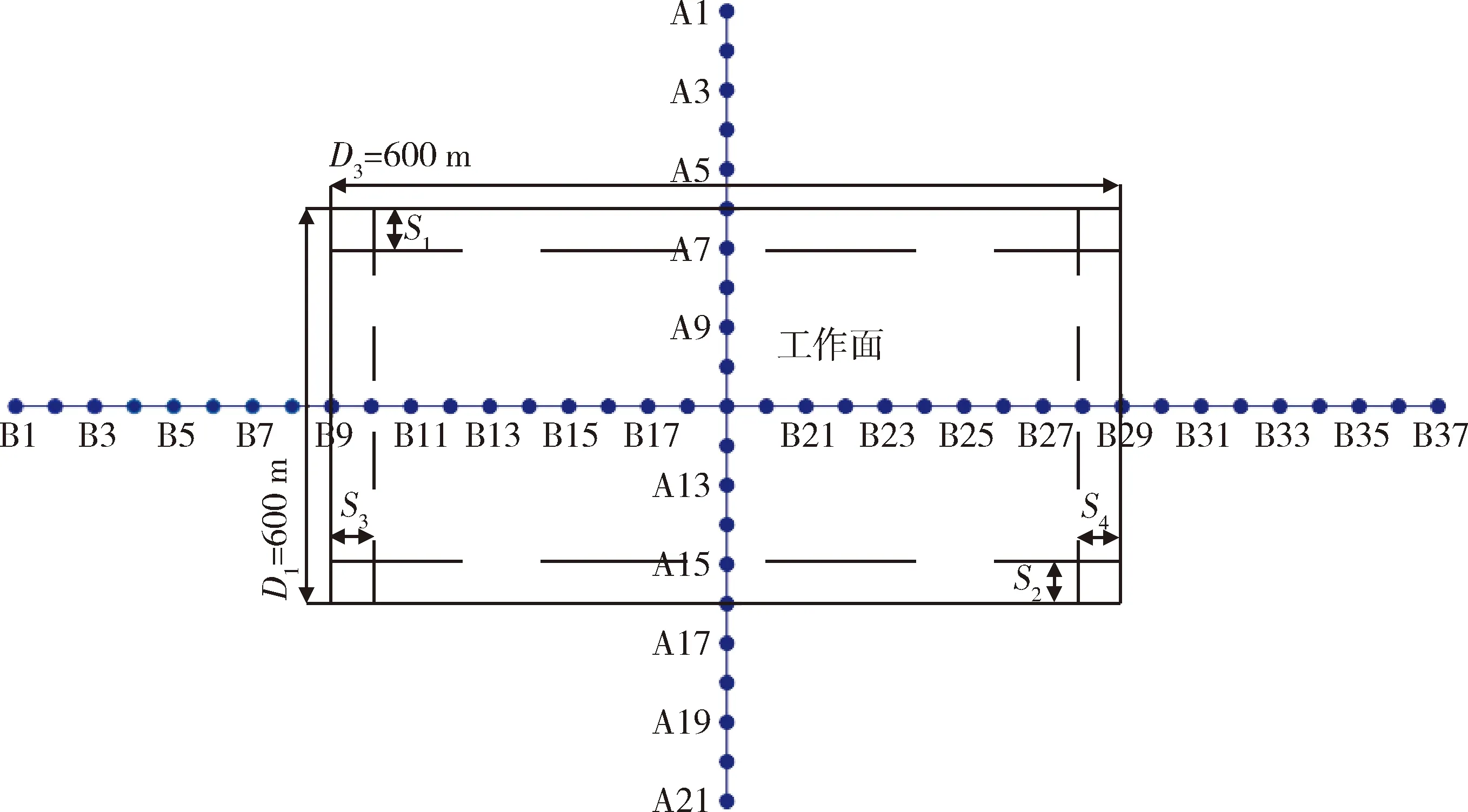
图2 模拟工作面设计图

2.2 BA参数反演准确性分析

智能算法在一定范围内具有随机性，为避免偶然误差对实验结果准确性的影响，在相同的实验环境下连续进行了10次BA参数反演实验。设置初始蝙蝠种群个数为400，最大迭代次数为100。以BA进行概率积分参数反演， 并将模拟实验参数预设值与BA参数反演值进行对比分析，通过反演参数中误差和相对误差来反映BA反演参数的准确性，实验结果见表2。

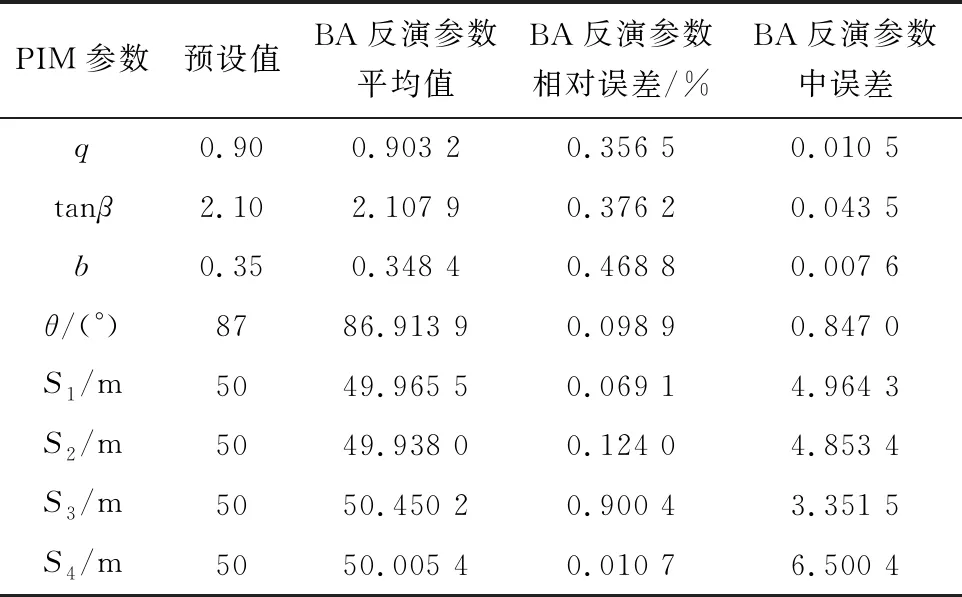
表2 BA反演参数值与预设值对比

由表2可知，BA反演参数相对误差方面，S1、S2、S3、S4、q、tanβ、b、θ反演准确性较高，相对误差均不超过1%，且在中误差方面，S1、S2、S3、S4的中误差均不超过7 m，q、tanβ、b、θ反演准确性较高，中误差均不超过1。由此可见BA反演PIM参数具有较高的准确性。

为了更好地分析BA算法的准确性，需要对下沉和水平移动的拟合情况进行分析，故通过10次BA参数反演实验取PIM参数均值，计算模拟工作面的下沉与水平移动值，具体曲线如图3和图4所示。由图3和图4可知，通过BA反演的PIM参数计算的下沉值和水平移动值拟合效果良好，达到预期精度，故BA参数反演准确度较高。

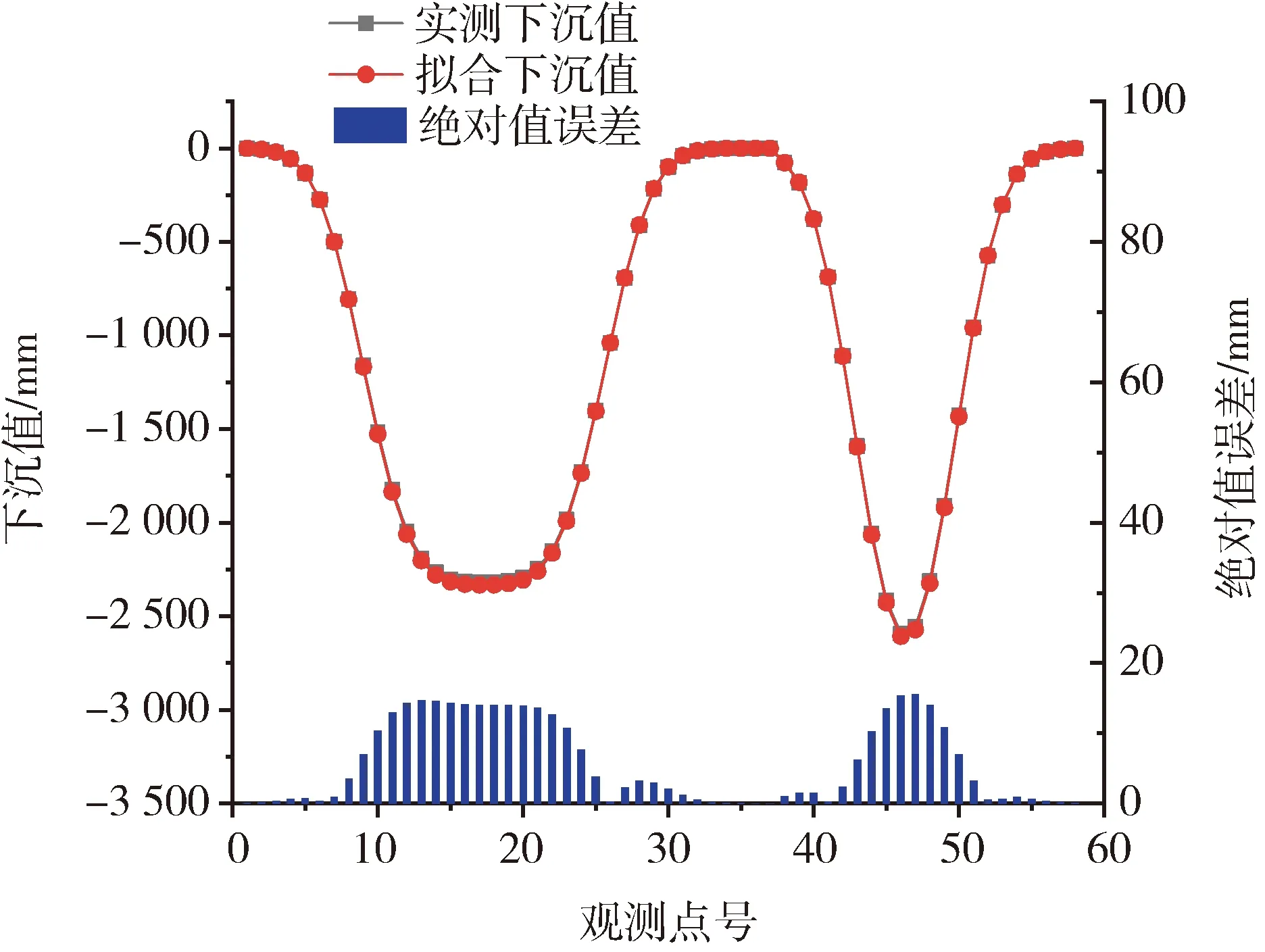
图3 BA模拟实验拟合下沉值与实测下沉值对比图

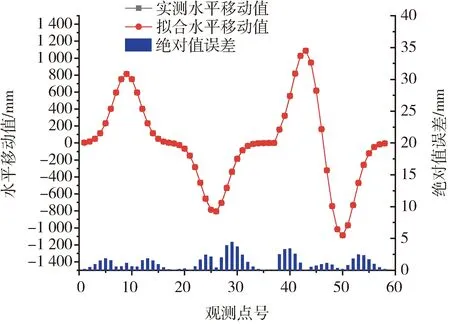
图4 BA模拟实验拟合水平移动值与实测水平移动值对比图

2.3 BA参数反演波动性及抗随机误差分析

为了进一步验证BA参数反演的稳定性，对模拟实验反演10次的PIM参数分别进行波动性分析，结果如图5所示。由图5可知，通过BA反演的PIM参数在真值附近波动范围较小，具有较好的稳定性。

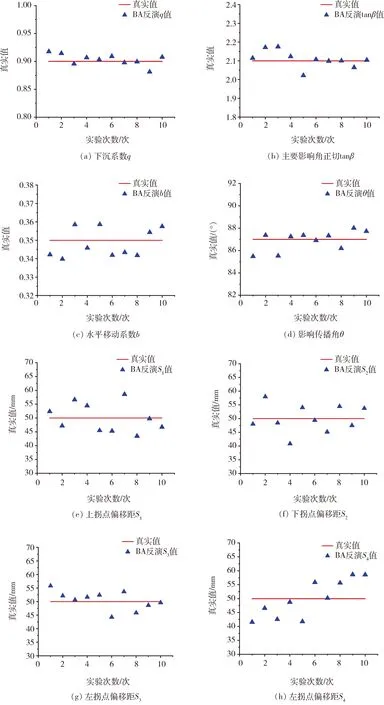
图5 模拟实验10次反演参数的波动情况

为进一步验证BA在反演PIM参数时是否对随机误差具有一定的抗干扰能力[15]，将模拟实验走向线和倾向线上共58个监测点的下沉值随机地先后减少5 mm、10 mm、15 mm，水平移动值随机地先后减少2 mm、4 mm、6 mm，再用三组具有随机误差的模拟监测数据通过BA进行10次PIM参数反演，最后与预设参数进行对比分析，结果见表3。由表3可知，在随机加入误差后，BA反演PIM参数仍具有较好的稳定性，说明BA反演PIM参数模型具有一定的抗随机误差干扰能力[16]。

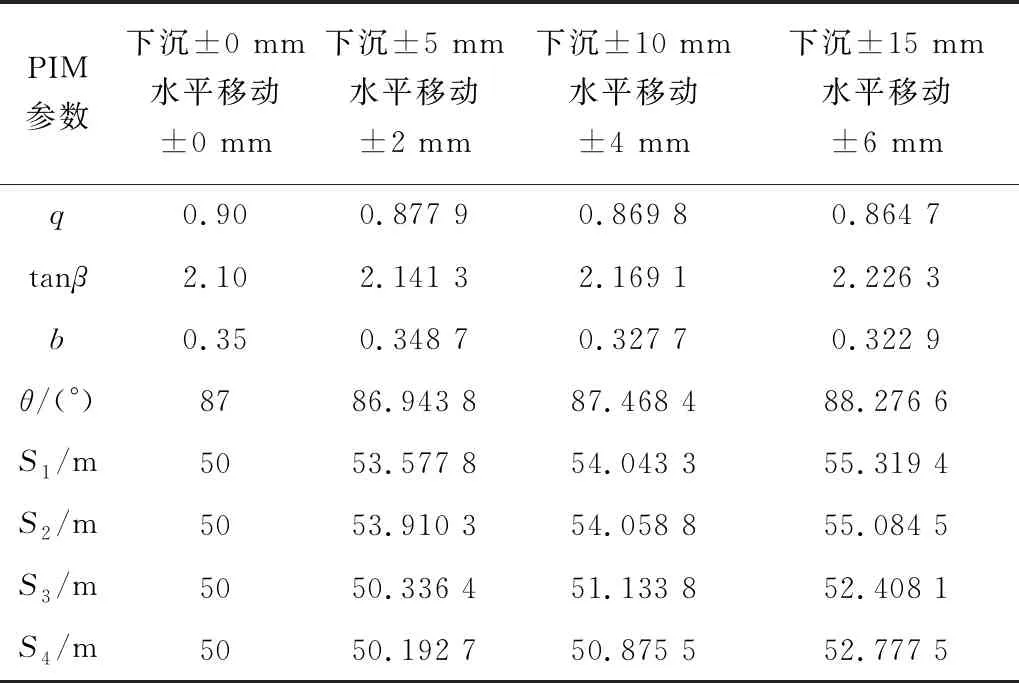
表3 BA反演PIM参数模型抗随机误差分析

3 工程实例

结合安徽省淮南市某煤矿1414工作面地表观测站[14]实测的下沉值和水平移动值对BA反演PIM参数方法进行分析，该工作面走向长度为2 120 m，倾向长度为251 m，工作面平均深度为735 m，煤层平均倾角为5°，平均采高为3.0 m。选取该工作面走向线上75个监测点，倾向线上47个监测点共122个监测点的实测数据为基础，利用BA反演10次PIM参数求取均值的方法计算预测的下沉和水平移动值并与监测点的下沉和水平移动值进行对比分析，并计算BA反演10次参数的平均值与中误差。其结果见表4。

表4 BA反演参数工程实例结果

由图6和图7可知，拟合下沉值和水平移动值曲线与实测曲线基本一致，监测点的拟合值与实测值之间的绝对值误差均在250 mm范围以内，而且BA反演10次PIM参数取平均值后，其下沉值与水平移动值的拟合中误差为116.34 mm。一般认为对下沉来说，拟合中误差小于最大下沉值的5%；对水平移动来说，拟合中误差小于最大水平移动值的10%；而本文所求的下沉值拟合中误差约为最大下沉值的3.5%，水平移动值拟合的中误差约为最大水平移动值的1.49%。满足上述条件，符合工程应用标准[17]。

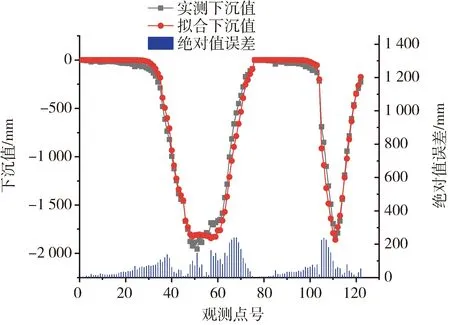
图6 BA拟合下沉值与实测下沉值对比图

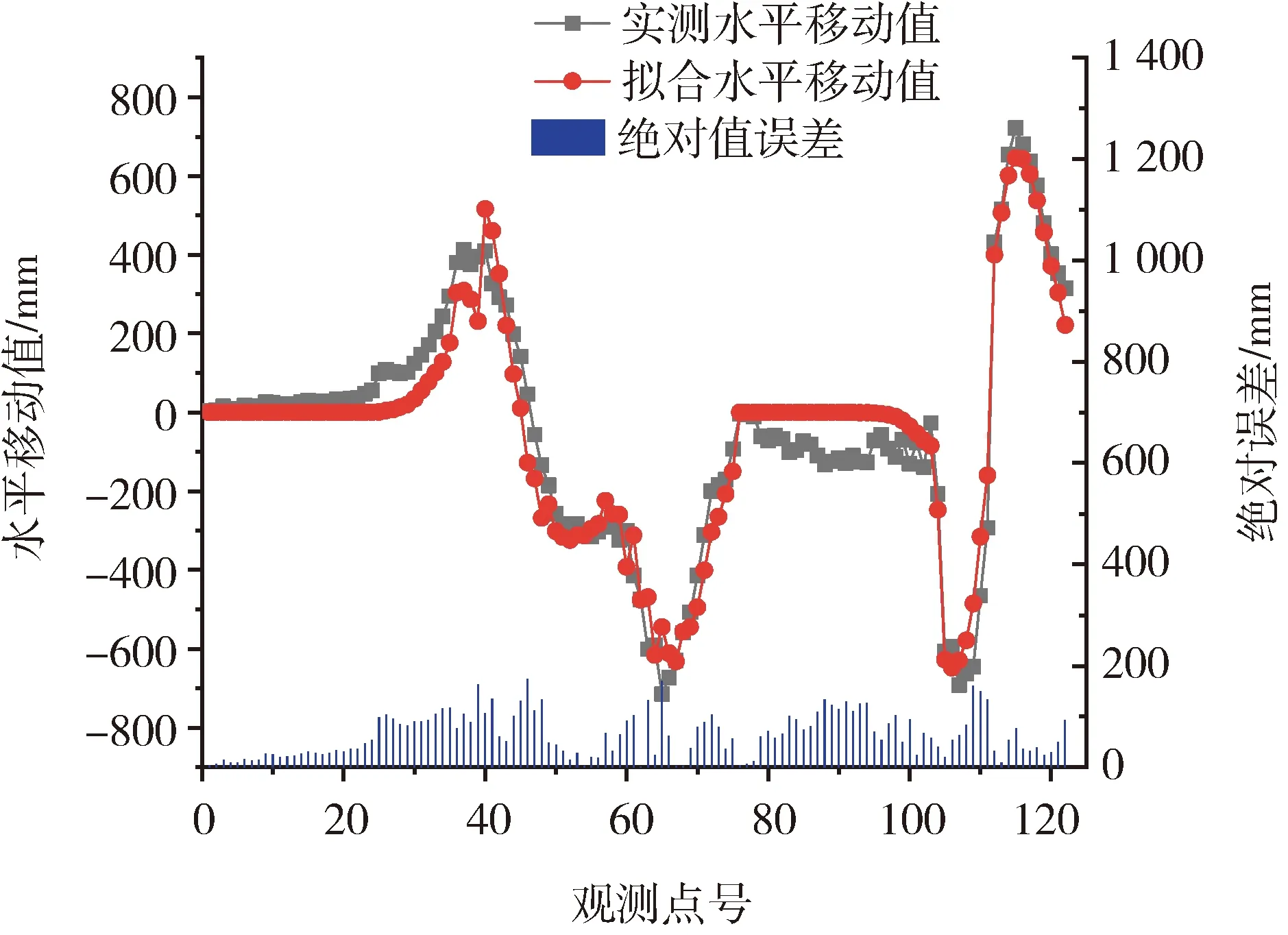
图7 BA拟合水平移动值与实测水平移动值对比图

4 结 论

1) 模拟实验：各预计参数q、tanβ、b、θ、S1、S2、S3、S4、反演相对误差均不超过1%且q、tanβ、b、θ反演中误差均不超过1，S1、S2、S3、S4反演中误差均不超过7 m；模拟实验验证了基于BA的概率积分参数反演模型的可靠性与准确性。

2) 工程实例：将BA算法应用于淮南市某煤矿的预计参数反演中，求解的预计参数分别为：q=1.03、tanβ=1.97、b=0.38、θ=86.66°、S1=-2.51 m、S2=-13.42 m、S3=60.36 m、S4=42.37 m，下沉及水平移动拟合中误差为116.34 mm，符合工程应用标准。

3) 在进行PIM参数求解时，BA算法原理简单、参数较少且易于编程实现等优势，对于附近矿区精准PIM参数反演具有一定的参考价值。