基于一维CNN的多入多出OSTBC信号协作调制识别

安泽亮，张天骐，马宝泽，邓盼，徐雨晴

（1.重庆邮电大学通信与信息工程学院，重庆 400065；2.重庆邮电大学计算机科学与技术学院，重庆 400065）

1 引言

正交空时分组码（OSTBC,orthogonal spacetime block code）[1-2]因分集增益高和接收端解码简便，在多入多出（MIMO,multiple-input multipleoutput）系统中得到广泛应用，能显著提升通信传输的可靠性。近年来，非合作通信场景下OSTBC信号盲处理研究受到广泛关注，但只有正确识别调制样式，才能准确解码得到传输信息，所以调制识别研究是OSTBC 信号盲处理中的一个重要研究方向。但现有调制识别研究主要针对单入单出系统，而对MIMO 系统调制识别的研究较少，且受空时编码和MIMO 信道影响，OSTBC 信号的调制识别变得更加棘手[3-7]，因此，非合作通信场景下OSTBC信号的调制识别具有重要的研究价值。

当前，针对OSTBC 信号调制识别算法主要分为2 类：基于似然函数和基于特征工程。其中，基于似然函数的算法[3-4]具有较优的识别精度，但其过高的计算复杂度和过多的先验信息需求，使其不适用于非协作MIMO-OSTBC 系统。基于特征工程的算法包含特征提取和分类判决2 个环节。1) 特征提取是指从截获的OSTBC 信号中提取深层特征，如高阶累积量[5-6]、高阶矩[5]和瞬时统计特征[6-7]，这些特征具有较好的调制特征表达能力，但都是基于人工专家经验设计的，特征选取的理论指导不足且缺乏通用性，在多类别OSTBC 信号识别中存在特征冗余和判决阈值设定困难的问题。2) 分类判决是指设计有效的分类器来完成OSTBC 信号识别任务。现有分类器大多基于机器学习算法，如K 最近邻（KNN,k-nearest neighbor）[5]、支持向量机（SVM,support vector machine）[5]以及决策树[6]。然而，特征工程方法的非线性拟合能力有限，识别精度存在提升的空间，且特征提取步骤烦琐，不利于实际工程应用。针对上述问题，应用驱动人工智能蓬勃发展的深度学习技术，能自动提取信号特征，简化任务复杂度，且其非线性拟合能力更强，可进一步逼近识别精度上限。例如，基于堆叠自编码器的深层神经网络（SAE-DNN,stacked auto encoder-deep neural network）[7]，学习信号高阶累积量和瞬时特征，相比机器学习算法有一定性能提升，但特征转换中存在信息损失，识别精度有待提升，且该算法假设信道状态信息已知，不适用于非合作通信场景。

受上述研究启发，本文提出一种基于一维卷积神经网络（1D-CNN,one-dimensional convolutional neural network）的多天线协作OSTBC 信号调制识别算法。首先，通过迫零（ZF,zero-forcing）盲均衡来减少信道衰落的影响，恢复源信号的特征表达能力，并通过最小化基于峭度的损失函数来盲估计信道矩阵，解决非合作通信场景下信道状态信息未知的问题；其次，充分利用深度学习在模式识别领域的前沿技术，并构建1D-CNN 来匹配一维输入信号特性，直接从天然无损同相正交（I/Q,in-phase/quadrature）信号中提取高维特征，避免复杂的特征转换；最后，为弥补单天线判决的不足，采用投票和置信度决策2 种融合策略，实现接收端多天线协作调制识别二进制相移键控（BPSK,binary phase shift keying）、4 相移键控（4PSK,4 phase shift keying）、8 相移键控（8PSK,8 phase shift keying）、16 正交振幅调制（16QAM,16 quadrature amplitude modulation）、4 脉冲振幅调制（4PAM,4 pulse amplitude modulation）5 种调制信号。仿真实验表明，所提算法能实现比现有算法更高的识别精度和更低的测试计算时间，拥有较高的工程应用前景。同时，所提算法能自动提取信号波形的高维特征，避免了烦琐的人工特征提取，提升了OSTBC 信号调制识别的智能化层级。

2 系统模型和数据集构造

2.1 系统模型

本文考虑一个MIMO-OSTBC 系统，收发端天线配置为M×N，系统模型和数据集构造流程如图1所示。首先，发送端通过符号调制器将二进制比特数据映射为K个符号流s=[s1,s2,…,sK]T，且s中各调制符号是独立同分布的；然后，通过空时编码器输出一个M×L的空时编码符号复矩阵X=C(s)=[x1,x2,…,xM]，其中L为发送时隙长度；进一步地，对X进行功率归一化，确保每根天线发射信号具有相同的单位功率；最后，功率归一化后的经过衰落信道后，接收端N根天线接收信号矩阵Y(s) ∈CN×L为

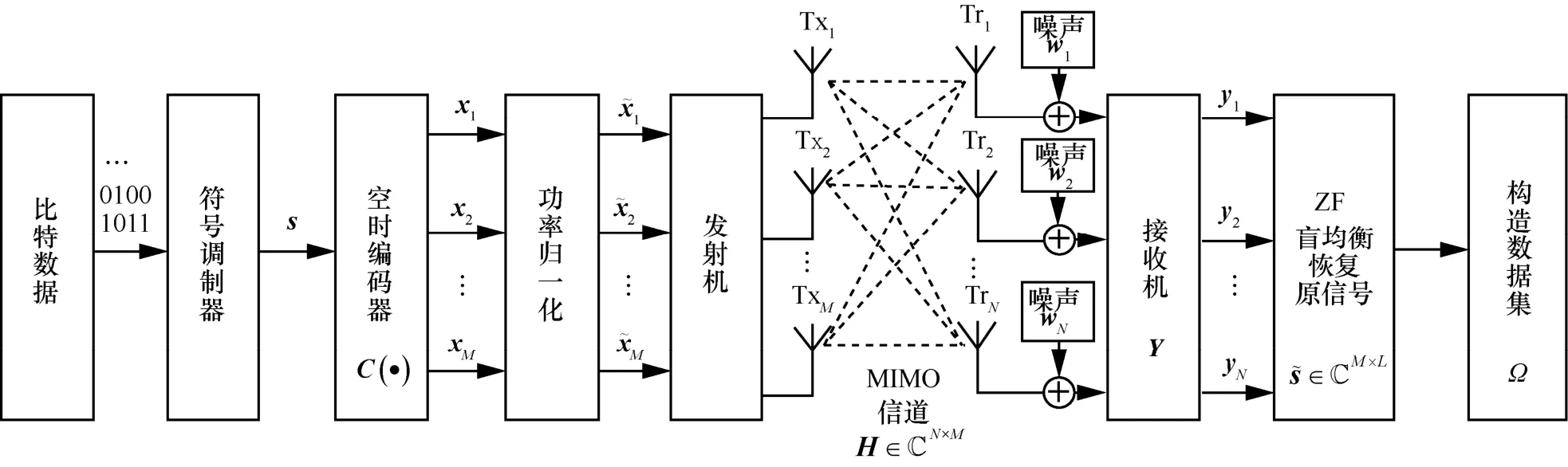
图1 系统模型和数据集构造流程

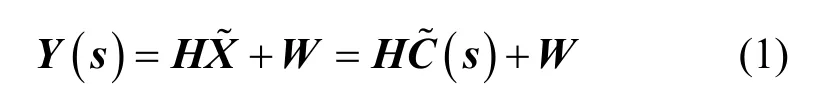
其中，W∈CN×L是N×L的加性白高斯噪声矩阵，与发送信号不相关；H∈CN×M是N×L的准静态平坦衰落信道矩阵，设定H为满秩矩阵（N＞M）；空时编码矩阵是对s的线性编码，即在时隙长度L内通过M根天线发送K个符号。

具体地，本文采用3/4 编码速率的OSTBC(3,3,4)编码方式，即符号流s在4 个时隙之中，通过3 根天线进行信号传输，对应的编码传输矩阵为

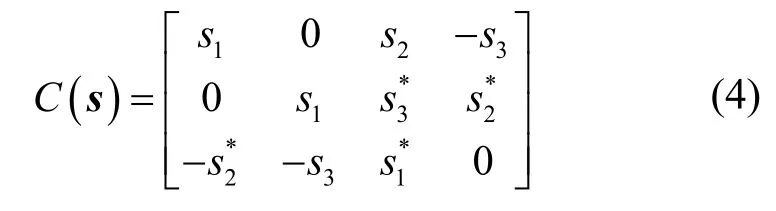
2.2 迫零ZF 盲均衡

由于受MIMO-OSTBC 系统和信道衰落影响，单个接收天线接收来自多个发送天线的混合信号，导致接收信号存在模糊性，因此，需采用ZF均衡来消除模糊性。现有MIMO-OSTBC 调制识别研究中[5,7]，通常预先用ZF 技术来预处理接收信号，提升后续信号的表征能力和调制识别准确率，但都假设接收端已知完美信道状态信息H，直接用ZF 技术来消除混合信道干扰，但在非合作通信场景下，接收端预先无法获得完美H，因此，需采用盲信道估计来获得信道估计值，本文通过最小化基于峭度的损失函数[8]来获得Hˆ 。首先，切分信号的实部和虚部，矢量化后的接收信号矩阵Y(s)为y。

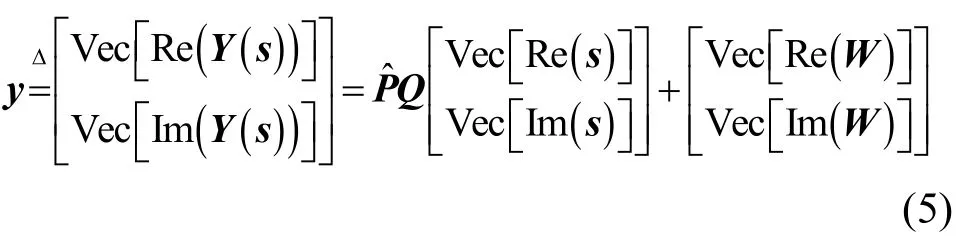
2.3 数据集构造

本节介绍数据集的构造流程。如图1 所示，当发射信号通过衰落信道后，接收机端通过ZF 盲均衡来恢复发射源信号，并对进行I/Q 分解来构造本文数据库。本文OSTBC 下的调制信号数据集Ω包含 5 种通信调制信号{BPSK,4PSK,8PSK,16QAM,4PAM}。为充分利用数据集的全面性，这里采用多种信噪比（SNR,signal-noise-ratio）样式，SNR 在[ −20 dB,18 dB]以2 dB 为间隔，共计20 种。仿真采用平坦瑞利衰落信道并设定其参数均值μ=0和方差σ2=1，ZF 盲均衡先采用最小化基于峭度的损失函数的方法获取衰落信道估计值，结合空时编码信息从衰落信号中恢复原始发送信号，并存储全部接收天线信号作为数据集，每根天线单次收集的信号作为一个有效样本。由于CNN 仅能处理实数数据，不能处理复数数据，因此需I/Q 分解一维复数数据（1×L）为二维数据（2×L），如式(14)所示。

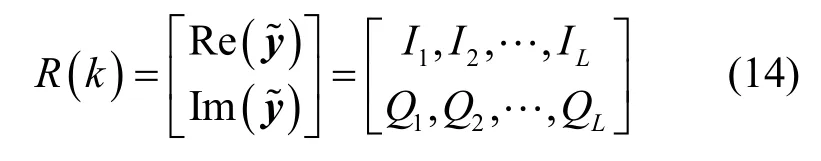
其中，I表示信号的实部，Q表示信号的虚部。本文的数据集尺寸为[T×2×L]，其中，数据集Ω的总样本数T=k m×ksnr×ks，km是信号种类数，ksnr是信噪比种类数，ks是每类样本每种信噪比包含的样本数。设km=5，ksnr=20，ks= 2 000。

为更好地理解源信号的恢复效果，通过星座图方式来可视化时序信号特点。在SNR=10dB下，MIMO-OSTBC 收发端天线配置为3×5，数据集可视化结果如图2 所示。在图2 中，发射源信号s通过空时编码、信道衰落和噪声影响后，接收信号星座点产生了偏移，具有一定的幅相误差，使星座图出现混淆模糊，从而降低了不同调制方式间的特征区分度，进而限制后续分类器性能。相比之下，ZF 盲均衡恢复的源信号的星座点模糊程度较小且聚类更明显，能有效缓解信道和OSTBC 编码影响，5 种调制方式间的区分度更大，较强的表征能力提升了调制识别的性能上限，而分类器只能无限逼近这一上限，因此，通过ZF 盲均衡提升信号表征能力是至关重要的。

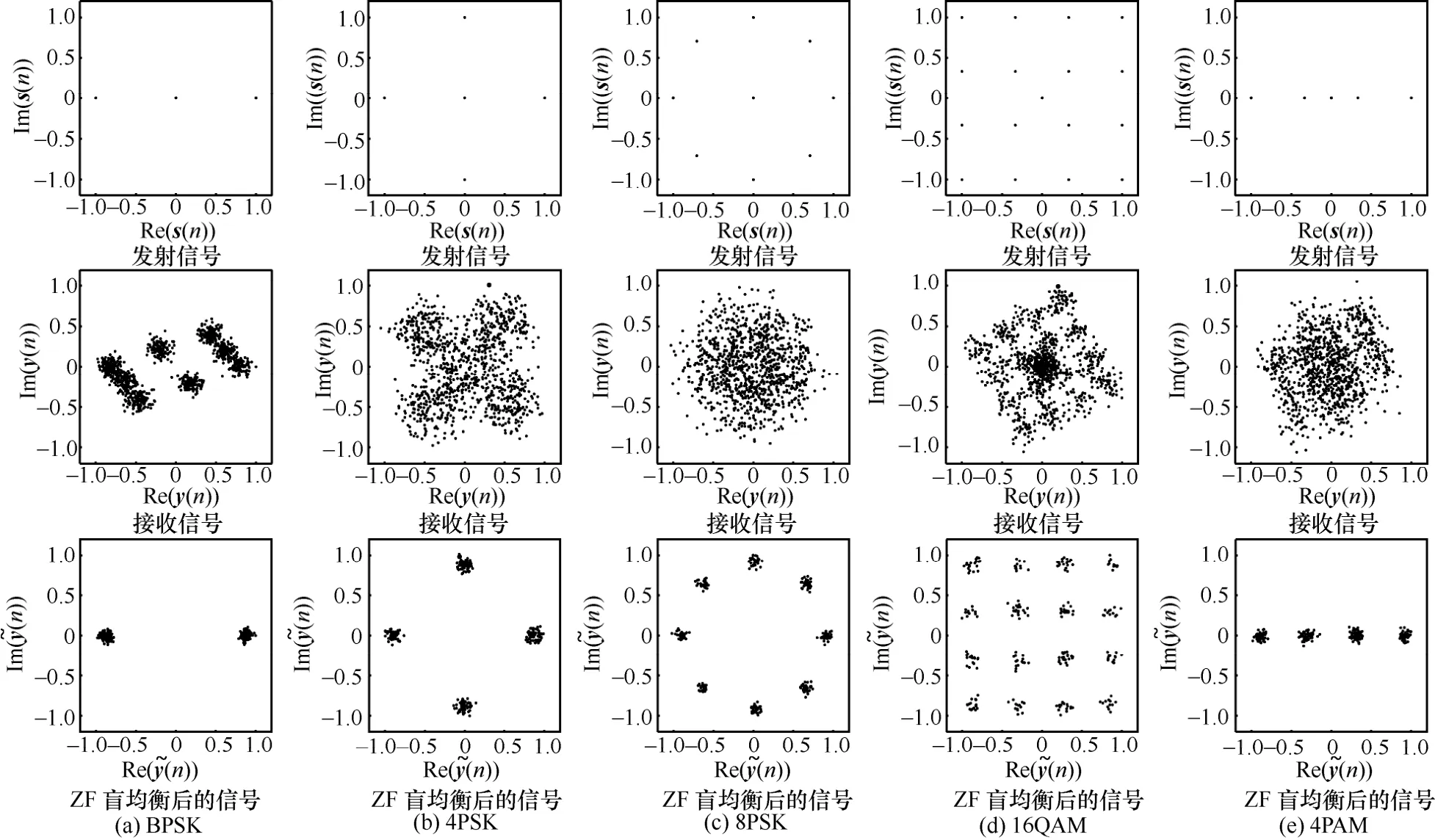
图2 数据集可视化（SNR=10dB，MIMO-OSTBC 收发端天线配置为3×5）

3 MIMO-OSTBC 系统调制识别算法

本文所设计的MIMO-OSTBC 系统调制识别原理如图3 所示。对于接收机，通过下变频、ZF 盲均衡、数据标准化以及I/Q 分解等一系列预处理以后，本文将2×N的数据样本输入识别网络，进一步完成特征提取和调制决策分类。

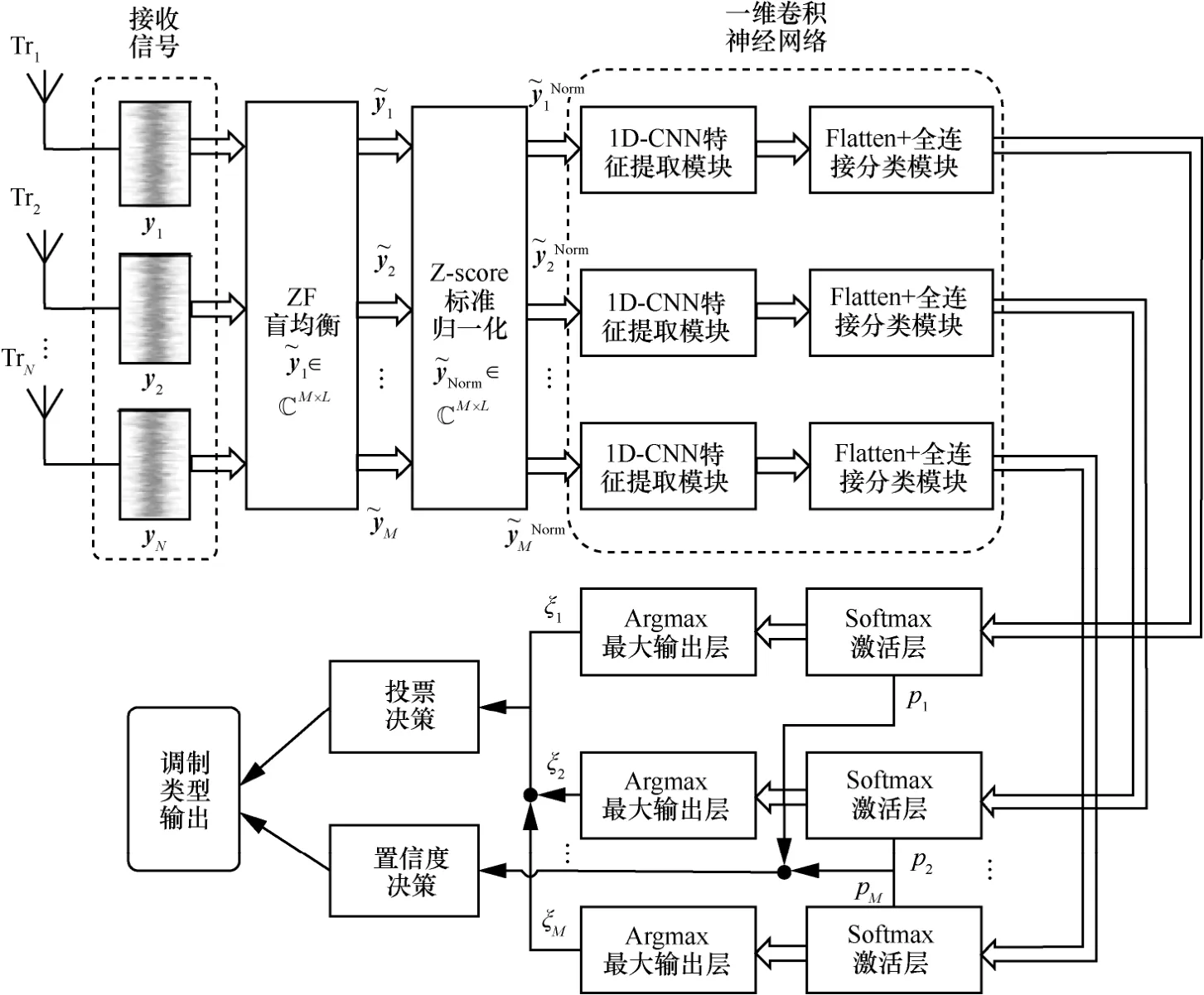
图3 MIMO-OSTBC 系统调制识别原理

3.1 Z-score 标准归一化预处理

考虑到发射信号经过衰落信道后，不同接收信号功率受影响程度不同，为统一各数据样本的数量级和增加可比性，并加快网络收敛速度和防止梯度爆炸，本文采用Z-score 标准归一化，基于输入样本的均值μ和标准差σ对进行标准化，即

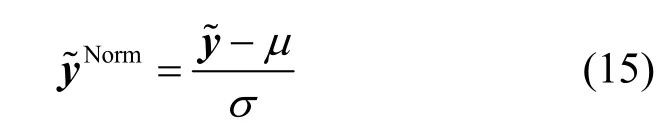
3.2 1D-CNN 一维卷积神经网络模型结构

图4 给出了本文所设计的一维卷积神经网络架构。为保证输入数据的信息无损和避免复杂的统计特征转换，本文模型输入采用最原始的I/Q 数据，其包含天然无损的特征信息，且数据预处理简易，这和文献[10-11]的研究思路相同。

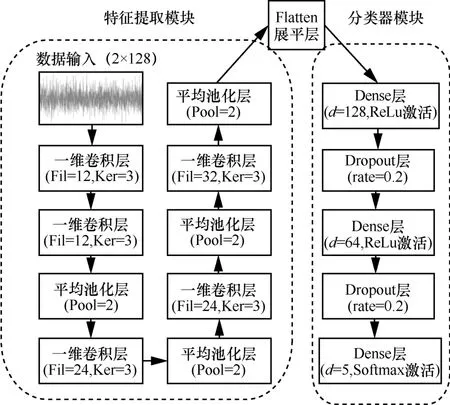
图4 一维卷积神经网络架构

3.2.1 特征提取模块

对于特征提取模块，由5 个一维卷积层（Conv 1D）和4 个平均池化层级联构成。Fil 为滤波器个数，滤波器可视为特征检测器，每个滤波器会从数据学习特征，采用金字塔形式来设计模型每层滤波器个数；Ker 为卷积核大小，借鉴主流的InceptionNet 和GoogleNet 中采用的3×3 小卷积核，本文选择Ker=3。

首先，为更好地适应时序数据的矢量特性和加快卷积运算，本文采用1D 卷积而不是2D 卷积，Conv 1D[12]的输入和输出数据是二维的，而Conv 2D[13]则对应三维输入输出，更适用于图像数据。Conv 1D 主要通过输入数据与卷积核的卷积运算来提取数据高维特征，且卷积核移动方向是单维的，Conv 1D 层输出为

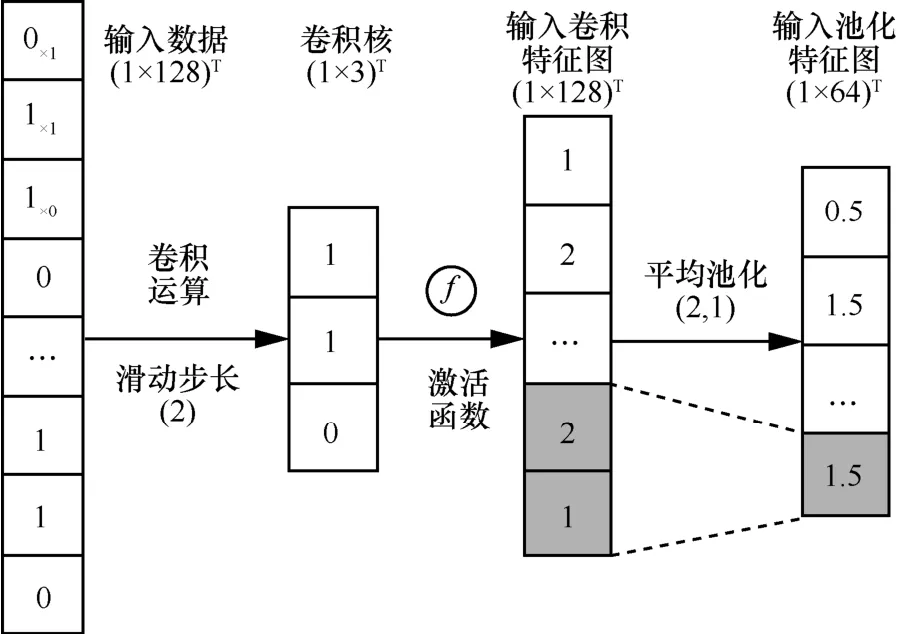
图5 一维卷积和平均池化原理

3.2.2 分类器模块

从特征提取模块到分类器模块，需要采用Flatten 层将二维输出特征图展平压缩成一维特征矢量。分类器模块包含2 个全连接层、Dropout 层和一个输出层，其中输出层采用Softmax 激活函数，Dropout 层能降低模型过拟合风险，提升模型稳健性，这里选择置零比例rate=0.2，即20%神经元将会被赋值零权重。2 个全连接层中都采用ReLU 激活函数，神经元节点数分别为128 和64，当给定全连接层FC-1 的输出特征矢量，全连接层FC-2的输出特征矢量为

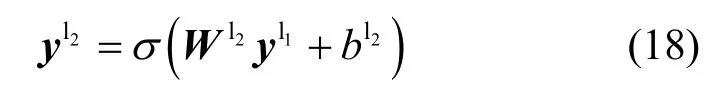
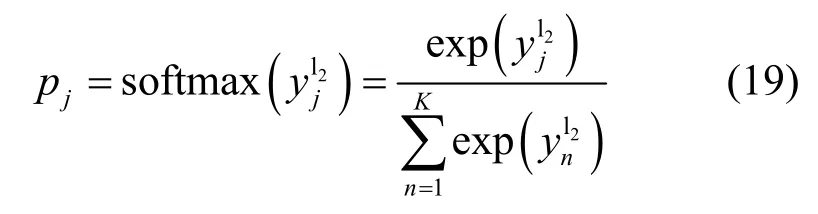
因此，在输出概率矢量p基础上，最后的调制识别问题就转变为基于最大后验准则的闭集分类问题，对于样本输入数据，判别输出结果ξ为

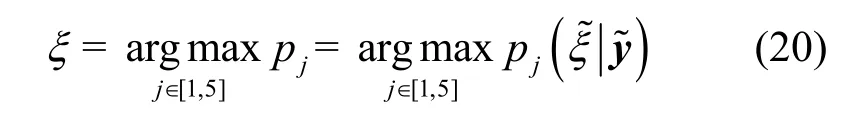
为减小训练复杂度，本文对所有天线接收信号集中训练，仅训练一个1D-CNN，而不是训练M个网络。在测试中，所有天线采用同一个网络测试。本文采用随机梯度下降策略来更新网络权重矩阵W和偏置b，一个训练batch 对应的损失函数为

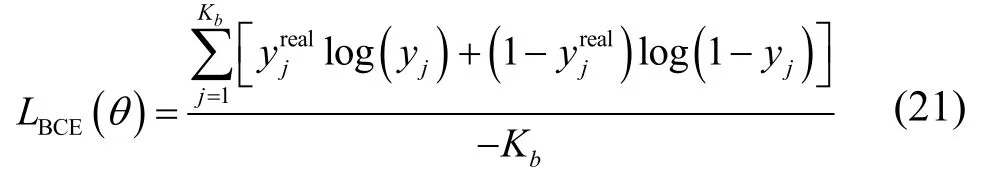
其中，Kb是一个batch 包含的样本数，log(⋅)是对数函数，和yj分别是真实标签和预测标签。

3.3 决策融合策略

本节主要介绍2 种决策融合策略。针对OSTBC(3,3,4)系统，在任一SNR 下，N路接收信号y受到的信道和瞬时噪声影响程度不同，在通过ZF 盲均衡恢复后的源信号有M条支路，各支路信号的盲均衡恢复效果有所差别，所蕴含的特征表达能力也不同，因此1D-CNN 分类器基于每一支路的信号所获得调制识别精度存在差别，且传统方法没有协作利用各支路的决策信息，识别精度上还存在提升的空间。为了提升最终的调制识别精度，本文采用决策融合策略来汇总各支路的判决信息，有助于降低系统误判的概率，具体如图3 所示。

3.3.1投票决策融合

投票决策融合是在M条支路的最终判决信息（Argmax 层输出的ξ）基础上，使用“少数服从”多数的评判方法给出了最终的决策结果V(x)，即

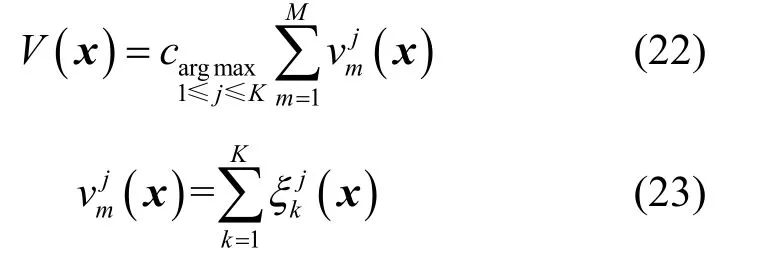
3.3.2 投票决策融合

不同于投票决策融合，置信度决策融合主要原理是利用M条支路的置信度信息，即Softmax 激活层输出的p，其中包含了每种调制类别的预测概率矢量，通过累加平均所有支路的置信度信息作为最终的判决依据，选择最大概率p对应的调制方式作为系统最终的预测类别P(x)，数学上可表示为

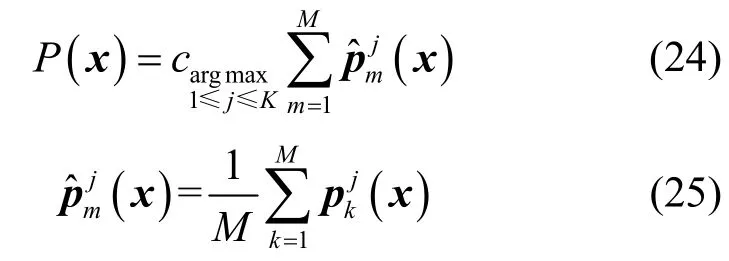
3.4 算法识别流程

本文所提出的MIMO-OSTBC 系统调制识别算法流程如算法1 所示。

算法1MIMO-OSTBC 系统调制识别算法

输入

1) 预处理的训练集Ψ1和未处理的测试信号y。

2) 随机初始化的1D-CNN 模型。

网络训练

1) 随机打乱训练样本Ψ1，按每128 个样本对应一个batch，将整个数据集分为m个batch。

2) 将m个batch 的训练数据和样本输入初始化的1D-CNN。

3) 采用SGD 方法来更新网络权重W和偏置b，当网络收敛时，保存训练好的模型参数。

测试信号ZF 盲均衡

1) 对信号进行下变频、载频估计等预处理。

2) 按照第2 节的ZF 盲均衡策略，将N根天线的接收信号y恢复为M路估计的源信号。

归一化预处理

决策融合输出

1) 投票决策融合。根据式(20)和式(23)计算M路信号类型出现个数，用式(22)汇总M路判决结果，投票选择出现最多的类型V(x)。

2) 置信度决策融合。通过式(19)和式(25)计算并统计M路信号上各类型出现置信度，用式(24)汇总M路置信度结果，选择最大概率对应的调制类型P(x)。

4 性能测试与分析

本节对所提算法识别精度进行仿真验证，采用的空时编码类型为OSTBC(3,3,4)。本文MIMOOSTBC 系统搭建和数据集生成在MATLAB 2019a仿真平台上完成，在TensorFlow2.0 环境下完成模型的搭建、训练和测试，所用GPU 型号为NVIDIA GeForce GTX 1660 Ti。按照6:2:2 的比例，整个数据集被切分为训练集、验证集和测试集，且每种调制类型有相同大小的样本子集，并使用Adam 优化器进行梯度更新，batch 批大小、轮次epoch 上限和初始学习率lr 分别设定为128、50 和0.001，对应损失函数为交叉熵损失函数。针对过拟合问题，这里采用早停策略，当验证损失在5 个epoch 内不再下降时停止模型训练。为评价所提识别算法性能，采用调制识别精度Pcc作为评价指标。

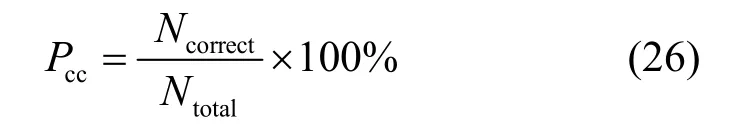
其中，Ncorrect表示测试集样本总数，Ntotal表示测试集中正确分类的样本个数。

4.1 模型整体识别精度

本节从3 个方面测试模型整体识别精度，包括ZF 盲均衡效果、不同OSTBC 码率以及不同调制类型。ZF 盲均衡预处理和不同OSTBC 码率对识别精度的影响如图6 所示，不管是OSTBC(3,3,4)还是OSTBC(3,4,8)，在整个SNR 范围内采用ZF 盲均衡的识别精度明显高于无均衡的情况，从图2 数据集可视化中也能看出，ZF 盲均衡能有效补偿信道衰落影响，恢复信号的星座点更集中且特征区分度更明显。在图6 中，不同码率的OSTBC 对识别精度影响较小，当SNR≥−4 dB时，采用ZF 盲均衡的OSTBC(3,3,4)和OSTBC(3,4,8)的识别精度都大于95% 。其中，OSTBC(3,3,4) 码率为3/4，而OSTBC(3,4,8)码率为1/2，对应空时编码矩阵为

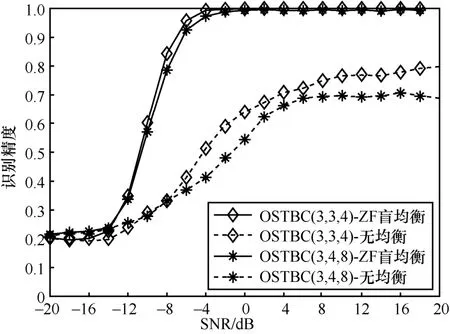
图6 ZF 盲均衡预处理和不同OSTBC 码率对识别精度的影响

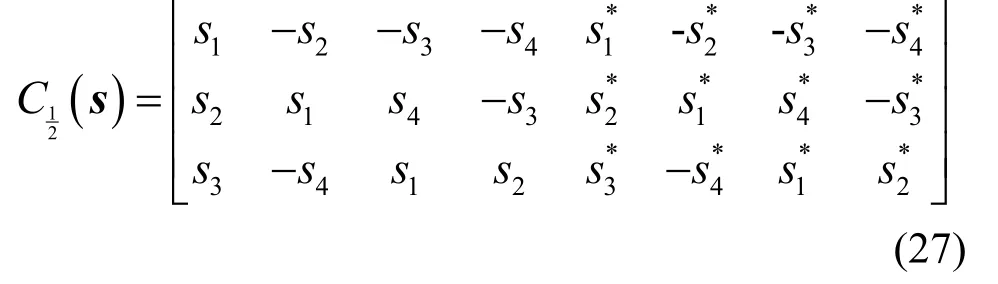
为对比不同盲均衡方法的预处理效果，表1从先验信息需求和平均识别精度两方面进行了验证。其中，ML（maximum likelihood）盲均衡表示最大似然盲均衡方法[2]，MUK（multiuser kurtosis maximization）盲均衡表示基于多用户峰态最大化的盲均衡方法[14]。首先，对于先验信息需求，MUK方法仅要求发射天线数，ZF 方法需要考虑空时码类型和盲信道估计值，ML 方法在ZF 方法基础上还要求已知调制类型，这与本文调制识别任务相矛盾，因此不能将ML 方法应用于本文中。其次，对于平均识别精度，相比ZF 方法和ML 方法，虽然MUK 方法的先验需求最低，但MUK 方法在整个SNR 范围内平均识别精度最低。综合考虑上述内容，本文选择ZF 方法来补偿信道和空时编码对调制信号的影响。

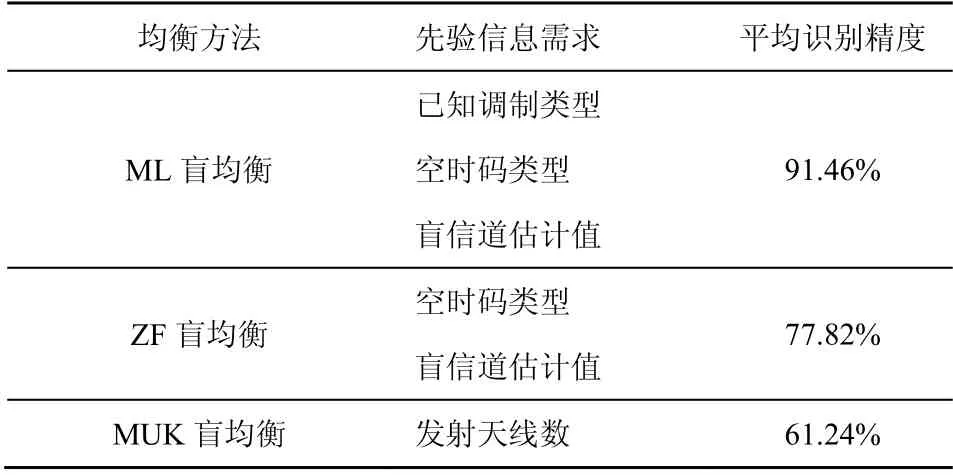
表1 不同盲均衡预处理方法的性能对比

不同SNR 下不同调制类型的识别度对比如图7所示。当SNR ≥ 0时，所有调制类型的识别精度都能达到100%，而SNR＜ 0时，调制识别精度有所下降。对于Mod-PSK 类间信号，随着调制阶数Mod的不断增加，识别精度不断下降，这是因为BPSK、QPSK 和8PSK 同属于圆形Mod-PSK 类调制，存在较多重叠区域。相比低阶BPSK、QPSK，高阶8PSK由于重叠度大，其特征更为模糊，这在图2 具象化的星座图上也可看出。此外，在低SNR 下，4PAM和16QAM 的识别精度要高于Mod-PSK 类信号。

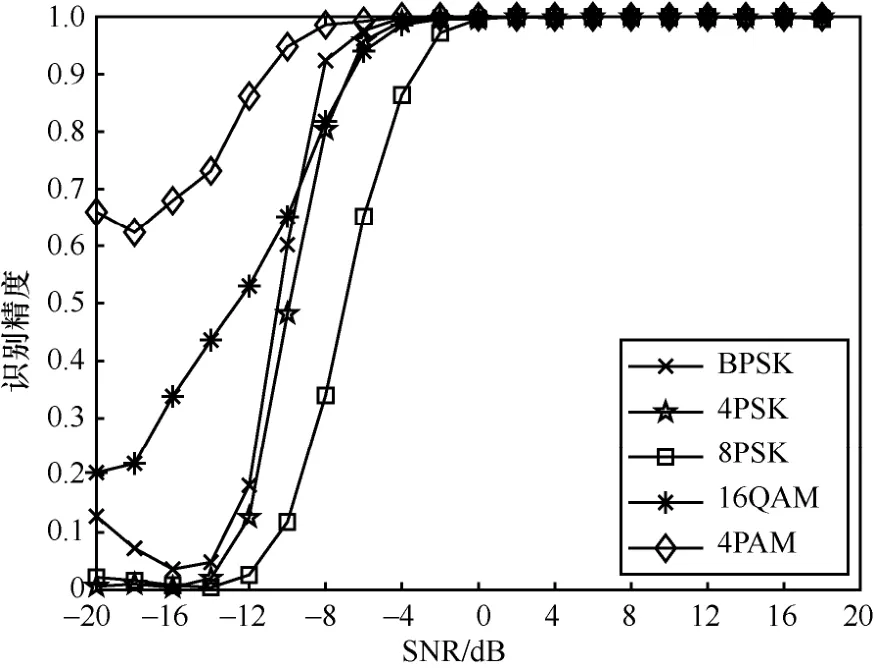
图7 不同调制类型的识别精度

4.2 不同算法识别精度和复杂度对比

本节从识别精度和算法复杂度2 个角度对比了本文算法和现有算法[5,7]。不同算法的识别精度对比如图8 所示。不同于基于特征工程的机器学习算法，所提1D-CNN 算法利用信号包含的天然无损的特征信息，并借助卷积神经网络强大的特征自动提取能力，因此所提算法识别精度优于现有算法，当SNR=−4dB时，所提算法能达到99.5%的识别精度，而SAE-DNN 算法[7]、SVM 算法[5]和KNN 算法[5]分别达到 95%、88%和 88%的识别精度。且在SNR ≥2dB时，1D-CNN 算法识别精度比SAE-DNN算法提高了10%，而比SVM 算法和KNN 算法提高了20%。

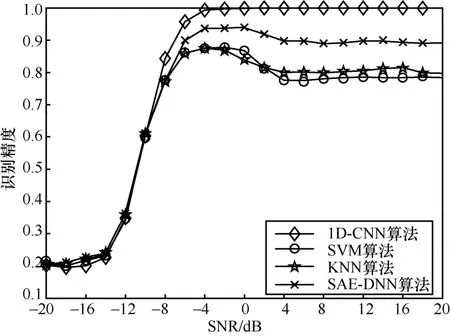
图8 不同算法识别精度对比

不同算法复杂度对比如表2 所示，主要包括2 个指标：内存消耗和测试时间。从测试时间来看，所提1D-CNN 算法和SAE-DNN 算法比KNN 算法和SVM 算法低了一个量级，处于亚毫秒级，且1D-CNN 具有最低的测试时间。由表2 还能看出，所提算法比KNN 算法和SVM 算法更小，占用更少的内存，有利于实际移动端的部署，此外，根据图8可知，虽然SAE-DNN 算法的模型内存消耗最小，但其识别精度低于1D-CNN 算法。因此，综合来看，所提1D-CNN算法能满足实时性要求且识别精度高于现有方法，在工业应用上拥有较高的发展前景。

表2 不同算法复杂度对比

4.3 不同决策融合策略下模型识别精度

不同决策融合策略下所提算法识别精度如图9所示。从图9 可以看出，不管是置信度决策融合还是投票决策融合，采用多路信号协作决策融合方法要比单一支路的决策识别方法性能更优，在识别精度为95%时，相比单一支路决策方法，置信度决策融合和投票决策融合方法分别存在1 dB 和2 dB 的性能增益。从图9 还可以看出，基于置信度决策融合策略比基于投票决策融合策略的识别精度更高，在SNR=−8dB时，置信度决策识别精度比投票决策方法存在20%的性能提升，因此，在本文仿真中，所提算法均采用置信度决策融合策略进行调制识别。

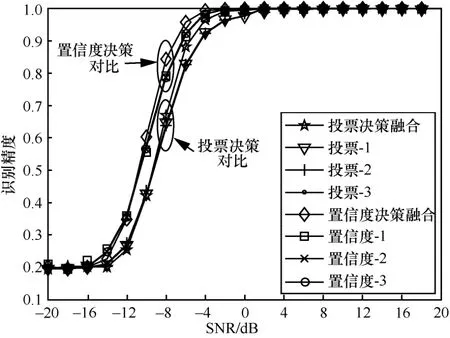
图9 不同决策融合策略下所提算法识别精度

4.4 不同接收天线下模型识别精度

不同接收天线数对模型识别精度的影响如图10所示。对于OSTBC3 系统，发射端天线数Tx 设定为3。由图10 可知，随着接收端天线数Tr 的不断增大，模型识别精度随之上升，这是因为收发端天线数差值 Δ=Tr − Tx 越大，系统分集增益越大，对应的系统SNR 增益越大，可有效降低高斯白噪声的影响和不同调制信号间特征间的模糊度，从而提升系统识别效果。从图10 可以看出，当SNR=−8dB时，从Tr=4到Tr=8，系统约有30%的识别精度提升。

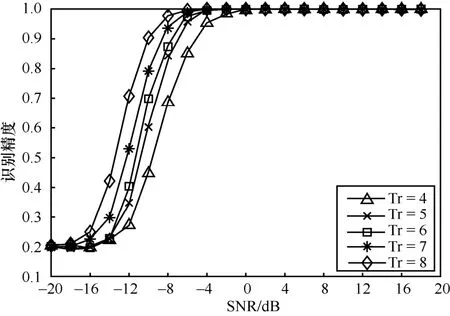
图10 不同接收天线下所提算法识别精度（Tx=3 ）

4.5 不同信道估计误差 下模型识别精度

为了衡量所提算法对信道估计误差的稳健性，实验测试了不同信道估计误差对所提算法识别精度的影响，如图11 所示。带有估计误差的信道矩阵为，其中，E是误差矩阵，其服从均值为0、方差为的高斯分布；大小决定了估计误差大小。相比无估计误差，信号在有下识别精度有所下降，且随着不断增大，识别精度也随之降低。对于SNR=0，当≤0.3和≤0.1时，识别精度分别能达到90%以上和100%。因此，所提算法借助1D-CNN 所具备的强有力的自学能力，能有效改善一定程度的信道估计误差影响。

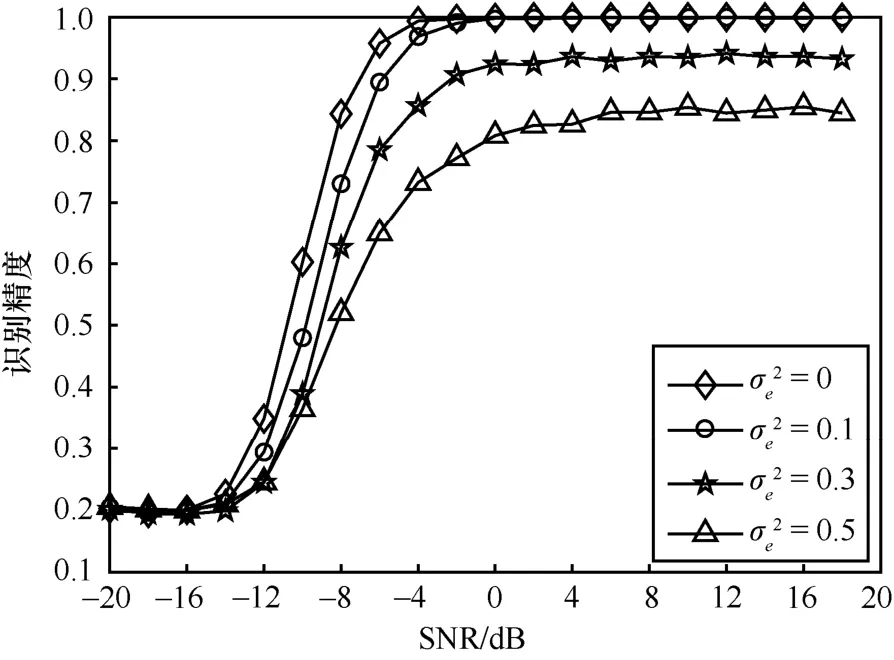
图11 不同信道估计误差 对所提算法识别精度的影响

4.6 不同网络参数下模型识别精度

本节验证了网络层数和卷积核大小对模型识别精度的影响。不同网络层数对模型识别精度的影响如图12 所示。图12 中1D-CNN-A、1D-CNN-B和1D-CNN-C 分别表示删除图4 中网络特征提取模块的最后2 层、4 层和6 层，而1D-CNN-Entire 表示完整的模型。从图12 可以看出，受限于浅层网络的特征提取能力，模型识别精度会因网络层数的递减而下降，而多个卷积层和平均池化层的级联，助推了信号高维特征的提取，可识别不同调制信号间的细微区别。

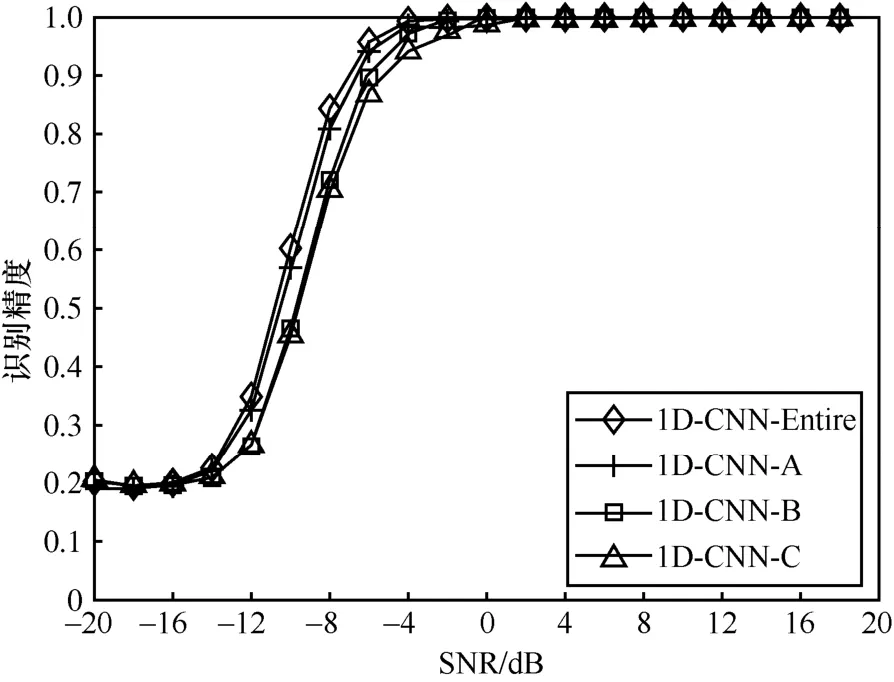
图12 不同网络层数下所提算法识别精度

不同卷积核尺寸Ker 对模型识别精度的影响如图13 所示。从图13 可以看出，对于完整的模型，Ker=2 到Ker=6 过程中，识别精度先增加后下降，且在Ker=3时识别精度达到最优。这是因为较小的卷积核对应感受野较小从而不能提取有效的特征；而较大的卷积核能获得更大的感受野，但会提取过多无用的特征，且无法堆叠更多的网络层，从而限制网络的特征提取能力。因此，通过该实验确定本文所用网络的卷积核为Ker=3。

图13 不同卷积核尺寸下所提算法识别精度

4.7 不同符号长度下模型识别精度

了不同样本符号长度L下的调制识别精度如图14所示。通过对原始数据进行稀疏化采样，每隔k个时间点对进行采样得到0 ≤i≤ [(n− 1)/k]。从图14 可以看出，识别精度随着L的增加总体呈增长趋势，但当L从128 增加到256 时，两者识别精度差异较小，且当SNR ≥−12 dB时，数据长度L=128能获得最优识别精度。此外，L过大会增加网络训练和测试复杂度，因此，本文数据集和模型架构选择L=128作为样本构造参数和模型输入尺寸。

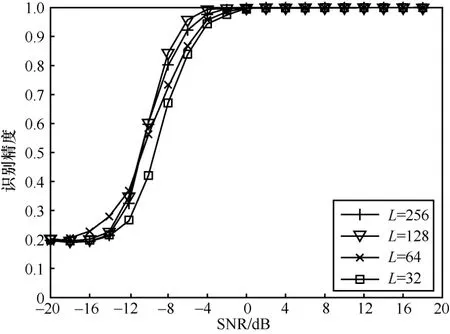
图14 不同符号长度下所提算法识别精度

5 结束语

本文基于ZF 盲均衡后的I/Q 数据形式，并结合前沿的深度神经网络模型，较好地完成了非合作通信场景下的MIMO-OSTBC 信号识别任务。所提算法直接使用内在无损的I/Q 信号信息，避免了复杂的特征工程，并使用ZF 盲均衡来消除信道干扰，最后借助多天线决策融合策略来提升系统整体调制识别率。对比传统算法，本文所提算法能获得更高的识别精度，在SNR≥−6dB和SNR≥−2 dB下识别精度分别能达到95%和100%，这表明本文算法能在低SNR 下很好地工作。此外，本文针对一维时序OSTBC 信号形式，构造了1D-CNN 来进行调制识别的设计思路，这也有助于未来其他类型一维时序通信信号的智能化调制识别研究。