公有云中身份基多源IoT终端数据PDP方案

2021-08-16王化群刘哲何德彪李继国

通信学报 2021年7期

王化群，刘哲，何德彪，李继国

（1.南京邮电大学计算机学院，江苏南京 210023；2.南京航空航天大学计算机科学与技术学院，江苏南京 210016；3.武汉大学国家网络安全学院，湖北武汉 430072；4.福建师范大学数学与信息学院，福建福州 350007）

1 引言

5G 等新兴技术的出现为物联网环境下数据转发的研究带来了新的机遇和挑战。5G 极大地提升了通信速度，能在无人驾驶、智能家居、智慧城市等方面广泛应用，5G 的诞生能改写物联网领域。云计算能够为远程计算机用户提供按需IT 服务，是继互联网经济繁荣以来的又一个重要IT 产业增长点。云平台能够为移动用户提供计算和存储资源，但存在外包存储数据被篡改的风险。

在公有云中，具体数据处理由公有云服务器（PCS，public cloud sever）执行。使用公有云具有以下优势：因为公有云提供了硬件、应用程序和带宽成本，所以操作简单且成本低廉；提供可扩展性以满足需求；因为用户只需为使用的东西付费，所以不会浪费资源等。在公有云中，数据不受用户控制。PCS 对外包数据的安全性和隐私性负有更多责任。但是，为了保护自己的利益，不诚实的PCS 可能会拒绝对丢失的数据负责。因此，确保数据所有者的远程数据完整性是重要的。在某些应用程序环境中，外包数据属于多个所有者，并且很敏感。在执行远程数据完整性检测时，必须确保验证者不能获取所存储文件内容的任何信息。同时，验证者必须确保检测的数据属于指定的多个所有者。但是，谁有能力检测远程数据的完整性？为了保护数据隐私，只能由数据所有者授权的验证者执行远程数据完整性检测。PKI（public key infrastructure）需要公钥证书的分发和管理，会产生相当大的消耗，例如证书生成、交付、吊销、更新等。身份基公钥密码体制消除了复杂的证书管理，为了提高效率，研究公有云中多源物联网（IoT,Internet of things）终端数据身份基完整性检测非常必要。

当海量数据存储在PCS 中时，轻量级远程数据完整性概率检测是一种可行的方法。可证数据持有（PDP,provable data possession）是一个重要的远程数据完整性概率检测模型。基于RSA 加密技术，Ateniese 等[1]在2007 年提出了PDP 模型和设计方法。然后，文献[2-3]提出了PoR（proof of retrievability）模型。近年来，PDP 模型和方案设计得到了进一步发展。

利用区块链技术，研究人员相继提出了高效的私有PDP 方案[4]、无可信中心PDP 方案[5]、动态PDP 方案[6]等。为解决复杂证书管理问题，基于双线性对或RSA 假设，一些高效的身份基PDP 方案被提出[7-8]。当远程数据需要动态处理时，如插入、删除等，动态PDP 方案是必要的[9-10]。另外，可迁移的远程数据PDP 方案[11]、匿名PDP 方案[12]等相继被提出。

在某些特殊情况下，数据属于多个所有者。例如在工业物联网中，需要多个物联网节点协作交互，感知物理空间数据，并将这些数据存储在远程云服务器中。多所有者数据管理已成为重要的研究领域，在公有云中研究其完整性检测非常重要。现有PDP 方案都不是多源PDP，因而不适合本文的场景。本文提出的PDP 方案不仅适用于多源数据，并且是基于身份的，消除了复杂的证书管理，提高了效率。

本文主要贡献如下：提出了公有云中身份基多源IoT 终端数据PDP 概念，给出了形式化定义、系统模型和安全模型；使用RSA 和一些相应的困难问题，设计了一种有效且安全的身份基多源IoT 终端数据可证明数据持有（ID-MPDP，identity-based multi-source IoT terminals provable data possession）方案。安全性分析和性能比较表明，本文的ID-MPDP方案是可证安全和有效的。

2 系统模型、安全模型和预备知识

2.1 系统模型、安全假设和形式化定义

系统模型。本文系统由以下网络实体组成：系统管理器、私钥生成中心（PKG,private key generator）、PCS、数据所有者、验证者。

1) 系统管理器：生成系统参数。

2) PKG：可信第三方，为用户生成相应的私钥，也有助于验证者完成远程数据完整性检测。

3) PCS：具有大量存储空间和计算资源来处理用户数据。

4) 数据所有者：即多源IoT 终端，将大量数据上传到PCS 进行存储和计算。本文中，用户指IoT终端。

5) 验证者：通过与PKG 交互检测远程数据完整性。

信任假设。PKG 得到所有其他实体的信任。PKG 不能与所有其他实体（包括PCS、数据所有者、验证者）合谋。验证者不能与PCS、数据所有者合谋。对于属于n1个所有者的已处理文件F，允许PCS 与最多n1− 1个所有者合谋。

ID-MPDP 方案形式化定义如定义1 所示。

定义1ID-MPDP 方案。其包括5 个算法：SetUp、KeyGen、TagBlock、GenProof 和CheckProof，具体如下。

1) SetUp(1k)→系统参数。输入安全参数k，输出系统参数。

2) KeyGen(ID)→xID。输入用户身份ID，输出用户私钥xID。

3) TagBlock (F j,xIDi,IDi∈U)→Tj。输入数据块Fj，U中用户交互生成相应的标签Tj，并将(F j,Tj)上传到PCS。其中，U表示参与协议的用户集。

4) GenProof(chal)→V。输入挑战chal，PCS生成完整性检测证明V，并将V发送给验证者。

5) CheckProof(chal,V)→成功/失败。输入挑战chal 和响应V，如果有效，则返回“成功”；否则，返回“失败”。

2.2 安全模型

ID-MPDP 方案必须满足以下安全要求。

1) GenProof 只能由数据所有者授权的验证者执行。

2) 授权验证者不需要文件和标签的完整副本。

3) 修改某些存储的数据后，恶意证明者（即PCS）只能以很小的概率通过验证者的检测。即使PCS 与部分数据所有者串通，它仍然只能以很小的概率通过验证者的检测。

定义2不可伪造性。对于公有云中的多所有者数据，如果任何PPT 敌手A（即恶意PCS 和部分所有者）都无法伪造ID-MPDP 方案，A赢得游戏的概率可以忽略不计。游戏来自挑战者S与敌手A的交互，游戏如下。

1) 初始化。生成系统参数和数据所有者的公私钥对，并将系统参数和数据所有者的公钥发送给A。如果某个文件F存在n1个数据所有者，S将n1− 1个数据所有者的私钥发送给A。

2) 请求。A将预言机请求自适应地发送给S，S响应这些请求。

①哈希预言机。收到哈希请求后，S用相应的哈希值响应A。

② KeyGen 预言机。收到身份后，S会生成相应的私钥并将其发送给A。

③TagBlock 预言机。收到TagBlock 请求Fj后，S计算数据块标签Tj并将Tj发送给A。

3) 挑战。S向A发送挑战chal，限制条件是，至少有一个挑战数据块没有发给TagBlock 预言机。

4) 伪造。根据chal，A计算并返回证明V给S。

在上面的游戏中，如果响应V以不可忽略的概率通过S的检测，则A获胜。

定义3(ρ,δ)安全[8]。如果PCS 篡改了全部数据块−标签对的ρ部分，验证者以至少δ的概率检测到该篡改，则ID-MPDP 方案是(ρ,δ)安全的。

2.3 预备知识

1) RSA。RSA 密码系统由Rivest、Shamir 和Adleman 于1978 年发明。在标准RSA 中，n=pq是2 个同样大小的大素数的乘积，公钥e满足1 ≤e≤φ(n)的整数，且e和φ(n)互素，即gcd (e,φ(n))=1，其中φ(n)=(p− 1)(q− 1)是欧拉函数。求解方程ed=1modφ(n)得到私钥d。

定义4RSA 问题[13]。设n=pq是2 个同样大小的大素数的乘积，给定公钥n,e,y∈，RSA 问题是计算的模数y第e个根x，使xe=ymodn。

A解决RSA 问题的成功概率为

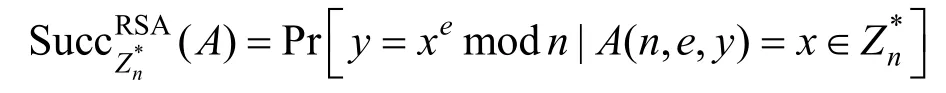
对于任何概率多项式时间敌手A，如果可忽略不计，则RSA 假设成立。

2) 二次剩余[13]。如果存在一个整数x使x2≡zmodn，则整数z为二次剩余；否则，z为模n的非二次剩余。

3 ID-MPDP 方案与安全分析

3.1 具体方案

假设上传的数据块−标签对的最大数量为，文件F可能通过使用纠错码（例如Reed-Solomon 码）进行编码将上传到PCS。F分为个块 (F1,…,Fnˆ)。本文中所用符号和说明如表1 所示。

表1 符号和说明

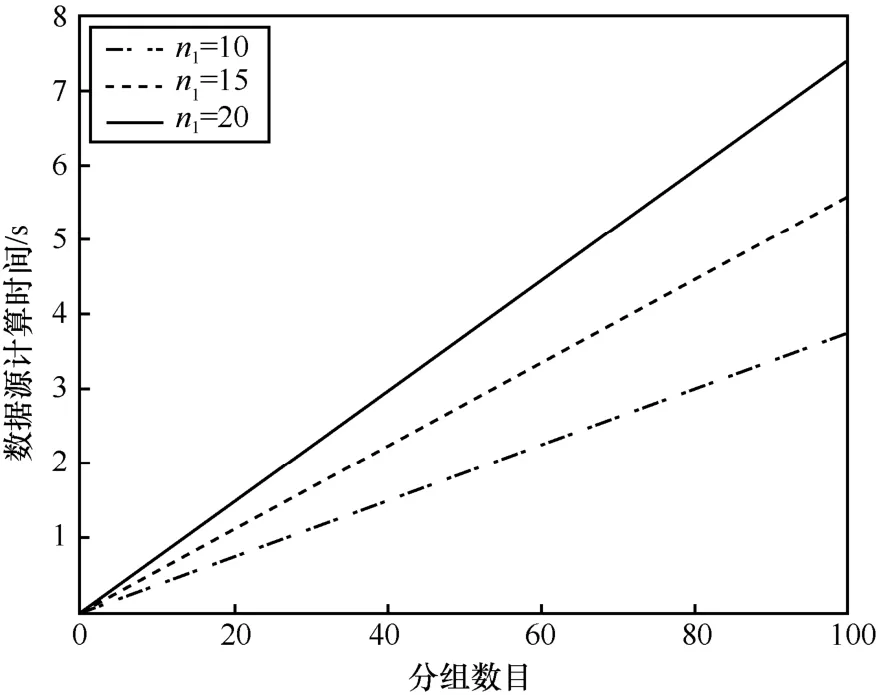
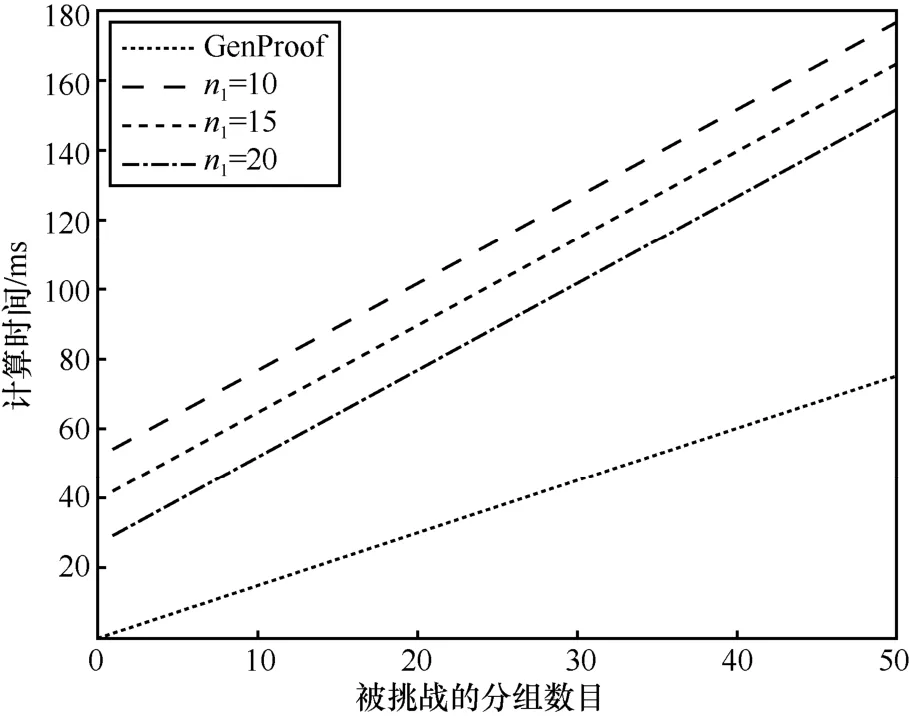
SetUp(1k)。n1表示数据所有者的数目，k表示安全性参数。选取 2 个素数e和e′，其中2k≤e,e′≤22k且2kn1

如果等式成立，验证者输出“成功”；否则，验证者输出“失败”。

3.2 安全分析

ID-MPDP方案的正确性分析和安全性分析如下。

定理1如果上传的数据块−标签对有效，即数据所有者和验证者是诚实的，并且数据没有被篡改，那么上传的数据块−标签对能够通过验证者的完整性检测，即CheckProof 满足正确性。

证明正确性来自以下推导。

4 性能分析

4.1 计算消耗

假设存在一个文件F，它属于n1个数据所有者。将文件F分成个数据块。在KeyGen 阶段，对于身份ID，PKG 需要执行哈希函数H1和以整数n为模的指数算法。在TagBlock 阶段中，对于单个数据块，每个所有者将计算一次哈希函数H3、4 次模幂n计算和2n1− 1次乘运算。对于挑战，PCS 将执行2c次幂运算和2(c− 1)次乘运算，执行2c− 1次加法和c次乘法。在CheckProof 阶段中，验证者将执行c+n1+1次幂运算和c+n1− 1次乘运算。另外，PKG 将计算m odφ(n)和一次幂运算。

4.2 通信消耗

RSA 的有效性取决于整数因子分解的计算困难性。1024 bit 的非对称密钥长度通常被认为是RSA 加密算法所需的最小长度。

数据上传一次可以全部完成，仅考虑完整性请求和响应引起的通信消耗。在完整性请求中，验证者将挑战 chal=(c,k1,k2)发送到PCS。换句话说，验证者将中的2 个元素和一个小整数c发送到PCS。当n的长度为1 024 bit 时，挑战的长度为。为了响应验证者的挑战，PCS 生成证明，其长度小于1024 × 3= 3 072bit。

4.3 降低数据块扩展率

4.4 可转换性

在CheckProof 阶段，秘密值D（i i=1,2,…,n1）是必不可少的。当验证者获得授权并获得秘密值Di时，它可以执行GheckProof 。否则，它将无法执行CheckProof。因此，当数据所有者将Di保密时，ID-MPDP 方案是私有远程数据完整性检测。当数据所有者将Di公开时，ID-MPDP 方案就是公共远程数据完整性检测。当数据所有者将Di发送给某些特殊的验证者时，ID-MPDP 方案就是指定验证者远程数据完整性检测。因此，该方案是可转换的。

4.5 方案比较

本节将ID-MPDP 方案的计算和通信消耗与文献[14-15]方案进行对比。本文方案和文献[14-15]方案都是使用RSA 设计的。由于哈希函数和加法效率较高，因此在比较中将它们省略。表2 给出了3 种方案的计算和安全性比较。在表2 中，n1表示数据所有者数，Exp 和Mul 分别表示乘运算和幂运算的时间消耗，Sig 和VeriCert 分别表示生成签名和验证证书的时间消耗。在PKI 中，验证来自证书颁发机构的证书是必不可少的。同时，本文还比较了它们的其他属性。文献[14-15]方案是在PKI 和基于身份的密码学中设计的，需要认证管理。本文方案完全基于身份的密码学设计，不需要认证管理。同时，本文方案满足可转换性，文献[14-15]方案不满足可转换性。另一方面，本文方案可用于处理属于多个所有者的数据，文献[14-15]方案不能用于处理属于多个所有者的数据。

表3将本文方案的通信消耗与文献[14-15]方案进行了比较，包括以下三部分：标签大小、挑战大小和响应大小。在表3 中，n表示RSA 中的安全大整数，表示总块数，n1表示所有者数。在文献[14-15]方案中，签名是必要的，用|Sig|表示签名长度，用|μ|表示合计块数量。

从表2 和表3 可知，ID-MPDP 方案具有以下优点。