基于高阶路径相似度的复杂网络链路预测方法

顾秋阳，吴宝，池仁勇

（1.浙江工业大学管理学院，浙江 杭州 310023；2.浙江工业大学中国中小企业研究院，浙江 杭州 310023）

1 引言

复杂系统普遍存在于人类社会中，常采用复杂网络对人类行为进行研究。随着近年来信息技术的不断发展，网络信息已成为大众获取信息、参与社交必不可少的媒介工具，而链路预测作为连接复杂网络与信息科学的重要桥梁，主要用于处理缺失信息的还原与预测，相关研究已受到国内外学者的广泛关注。复杂网络可对社会结构、生物系统和信息系统等进行有效建模，其中节点可表示网络中的个体或群体，边表示节点间的关系[1]。复杂网络研究已成为计算机科学、物理学、系统科学等学科的研究热点。现有研究多着重于复杂网络的演化机制、拓扑结构等特征，而链路预测则为其中的基本问题。在生物信息学领域中，链路预测在传染病、蛋白质等研究中都具有重要意义。链路预测在社会网络的相关研究中应用于好友预测及推荐。此外，还可通过链路预测实现科研合作推荐、知识产权推荐等[2]。链路预测技术有助于探测网络中个体间存在的潜在关系，可用于恐怖分子间的关系发现，以有效预防和制止犯罪行为[3]。由此可知，复杂网络链路预测技术在不同应用场景中存在广泛应用案例。

现有复杂网络常用图表示，其中节点表示个体或群体，边表示个体或群体间的交互行为。由于真实复杂网络中一般存在不断进入和移除的节点和边，故导致了系统的复杂性[4]。现今应用在复杂网络中的链路预测方法普遍存在精度不高、计算时间过长等问题，故提升链路预测的精度和效率是学术界亟待解决的重要问题。学术界通常将静态链路预测定义为被观测网络中寻找节点间的缺失链接，将动态链路预测定义为基于现有复杂网络是否可预测节点间存在未来链路的可能性。计算简单、效率高的基于相似性的链路预测方法最常见。通常包括基于邻域的链路预测方法（如公共近邻（CN,common neighbor）[5]、Jaccard 法[6]、Adamic/Adar（AA）法[7]、资源分配（RA,resource allocation）法[8]、偏好依附（PA,preferential attachment）法[9]等）和基于路径的链路预测方法（如Katz 指数[10]等），以探索网络中的全局信息。类局部方法采用的信息量与全局方法相同，计算效率与局部方法相同，故通常认为其为局部方法和全局方法间的权衡。

目前，已有较多文献对复杂网络中的链路预测问题提出了解决方法。基于相似性的链路预测方法中，节点对间相似性得分根据网络的局部/全局拓扑结构特征值计算得到。为提高链路预测方法性能，现有方法常在复杂网络拓扑特征中增加附加信息[11]，这在提升算法精度的同时也会使计算更加复杂。翟东升等[12]认为，从较长路径中提取较短长度的路径更具相关性，而高阶路径数量是由更复杂的线性指标决定的。Wu 等[13]以公共邻居节点聚类系数的形式提取三角结构信息，并利用真实复杂网络数据集进行验证。Rahimi 等[14]指出，根据网络拓扑结构，高连接节点的影响要小于网络中心度较高但连接数量较少的节点。Kumar 等[15]将聚类系数推广到存在高阶路径的复杂网络拓扑结构中以提取局部路径信息，并将扩展聚类系数概念应用于链路预测中。

通过对现有研究成果的梳理发现，复杂网络中的链路预测方法已受到了国内外学者的重视并得到了丰富研究。上述研究成果虽然对本文具有一定的借鉴意义，但也存在一些不足。首先，已有很多学者对链路预测方法开展了一系列研究，但多数集中在基于路径相似和公共近邻的方法（如吴翼腾等[16]），很少有利用高阶路径作为判别特征，并对种子节点对间的可用长路径实施惩罚进行链路预测的文献记录。其次，几乎所有的相关文献都只基于复杂网络图特征对链路预测方法提出了改进（如李永立等[17]），很少有在网络资源分配过程的启发下基于高度路径相似度进行链路预测方法设计的文献记录。最后，现有文献多在链路预测过程中使用了路径相似度指数，很少有在计算过程中基于公共近邻的连接惩罚限制信息泄露，以最大化描述节点间相似度节点对间信息流的文献记录。本文利用路径作为判别特征对复杂网络中的缺失链接进行有效预测，提出了基于高阶路径相似度的链路预测（HPS-LP,high-order path similarity link prediction）算法。然后通过惩罚公共近邻对信息泄露进行限制，以最大化描述节点间相似度节点对间的信息流。最后以高阶路径（定义为六度分隔理论）作为判别特征，对种子节点对间的可用长路径实施惩罚。

2 算法设计

大多数社会网络中会表现出小世界、聚类和无标度等拓扑性质。本文利用不同长度的路径来计算复杂网络中节点间的相似度，基于网络中的资源分配过程向目的地发送信息[8]。现有用于复杂网络环境的链路预测方法普遍存在精度不高、计算时间过长等问题，且还不能对信息泄露等问题进行有效控制。本文基于资源分配过程进行设计，根据目标节点接收到的信息量进行相似性分析。通过公共邻节点间的信息泄露来最大化节点间相似性，以提升复杂网络链路预测精度和效率，对信息泄露进行惩罚以实现有效控制。长度为2 的路径相似度可作为公共邻度，故可将任意节点对间路径长度为2 的相似性得分表示为

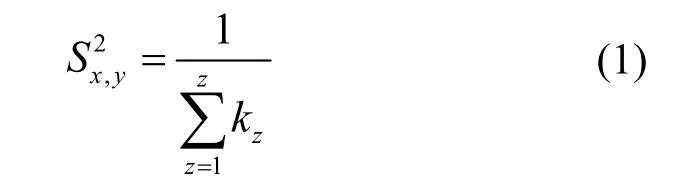
其中，kz表示节点z的度。而高阶路径相似度每一条长度大于2 的路径都可分解为长度为l−1 的路径和与其相连的一条边。而连接2 个节点的路径相似度得分为其分解所得长度为l−1 的路径的相似度得分与构成边的路径相似度得分的乘积，而较长的路径得分可表示为

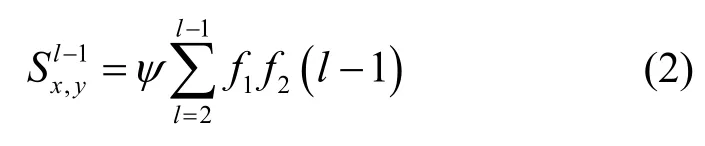
其中，f1和f2分别为路径边与上一周期中路径边的相似性得分，最高路径阶数为6（由六度分隔理论定义），ψ为惩罚较长路径的惩罚参数。路径相似度得分在第一次迭代中由路径长度为2 的得分计算得到（具体如式(1)所示）。路径长度得分f1和f2的累积效应可得到长度为3 的路径相似性得分。在本文所提算法中，使用类似方法迭代计算高阶路径相似度，如算法1 所示。

算法1HPS-LP 算法

输入复杂网络图G

输出得分矩阵

1) 计算路径为2 的相似度得分

2) 对每个节点对(i,j)do

3) 将公共近邻赋值为z

4) 计算路径得分

5) 基于步骤4)结果计算高阶路径得分

6) 循环计算高阶路径长度

7) 计算邻节点的高阶路径相似度得分

8) 结合上期末的路径相似度得分进行如式(2)所示计算

9) 基于步骤8)结果循环更新路径得分

10) 进行参数更新

11) 返回网络得分矩阵

算法1 中的输入为复杂网络图，输出为包含所有节点对得分的矩阵。该算法主要包括初始化、计算和更新3 个阶段，初始化阶段在网络的每个节点对间为矩阵Score 分配长度为2 的相似度得分，计算阶段基于2 个长度路径得分矩阵迭代计算更高路径长度分数，更新阶段根据前一阶段计算分数迭代更新上述2 个矩阵。

3 数值算例

3.1 数据说明与评价标准

本文使用国内外共10 个相关数据集对所提HPS-LP 法进行验证。本文利用Python 工具从新浪微博（爬取时间为2020 年4 月6 日至2020 年8 月12 日）、Twitter（爬取时间为2020 年3 月14 日至2020 年7 月29 日）、Facebook（爬取时间为2020年2 月10 日至2020 年8 月19 日）和Dolphins（爬取时间为2020 年3 月27 日至2020 年7 月13 日）的API 端口，以“华为”和“HUAWEI”为关键词选取30 个节点作为初始节点，爬取真实用户数据集作为实验的基础数据。Netscience[8]是2006 年编制的网络理论和实验的合著者网络，SmaGri[4]是HistCite 软件公司2009 年生产的Garfield collection引文网络，为科学网络搜索的结果。hep-ph 与astro-ph 表示2004—2009 年科研论文作者合作网络，其中hep-ph 为物理现象学领域，astro-ph 为天体物理学领域，且使用了至少撰写3 篇论文及以上的作者作为节点形成的网络[18]。dblp-collab 来自1999—2003 年DBLP 计算机科学文献[19]，其中dblp-collab 为计算机科学作者合作网络。本文使用五重交叉验证程序来评估所提算法的性能，并将所有数据以CSV 格式保存在MySQL 数据库中以便进行数据处理。使用Rapidminer 数据挖掘工具随机选取各用户评级数据的20%作为测试集，并将剩下的80%用户数据作为训练集。表1 为数据集统计信息。

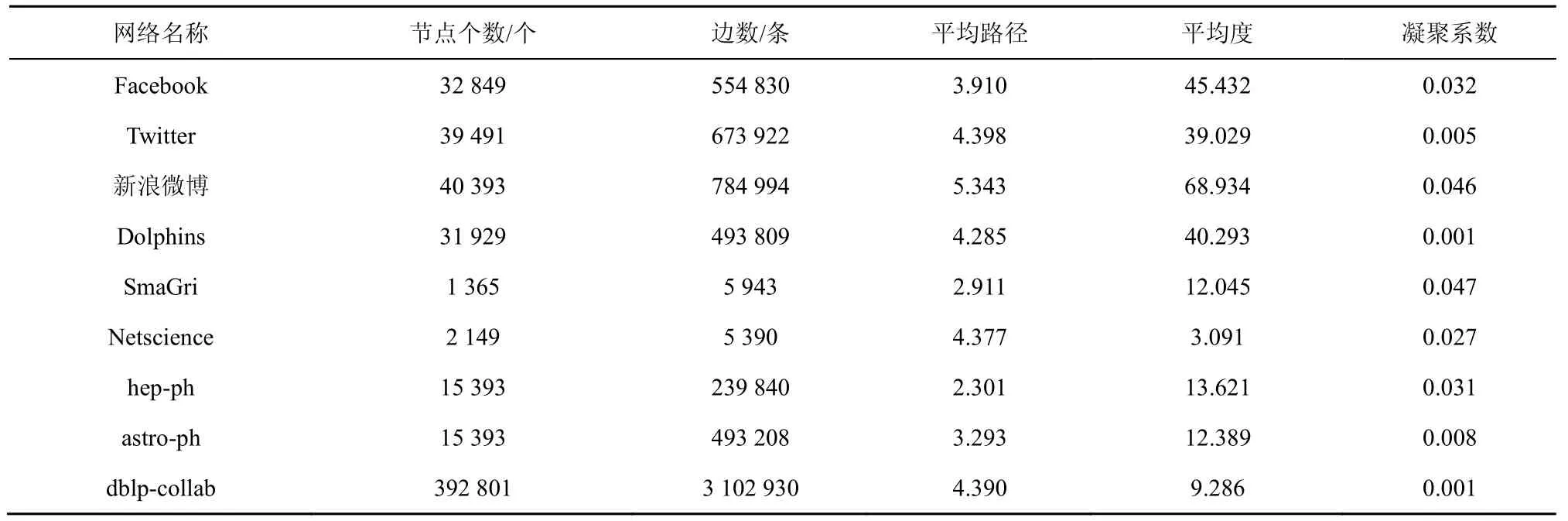
表1 数据集统计信息

链路预测问题通常被视为二分类任务，故用于二分类任务的大部分评估指标都可用于链路预测评估。在具有2 个类别的二分类任务的评估混淆矩阵中[13]，真正例（TP,true positive）表示正确预测链接的数量；真负例（TN,true negative）表示正确的未预测链接的数量；假正例（FP,false positive），表示错误预测链接的数量；假负例（FN,false negative）表示错误的未预测链接的数量。基于此，可得真正例率（TPR,true positive rate）、假正例率（FPR,false positive rate）、真负例率（TNR,true negative rate）和精确率（precision）等，其计算式可参考文献[20]。基于以下2 个指标进行评估，即ROC 曲线下面积（AUROC,area under the receiver operating characteristics curve）[12]和平均精度（AP,average precision）[15]。ROC 曲线是Y 轴上的真正例率（敏感性）和X 轴上的假正例率（1-特异性）间的曲线，曲线下面积值为[0,1]的数据可使用梯形规则累加计算得到。曲线下面积值越高，链路预测方法的性能越好。平均精度是基于不同召回阈值计算的单点汇总值，为区间[0,1]召回值的平均精度值。

3.2 基准算法

为体现本文所提HPS-LP 法的优越性，将所述方法与多种非监督结构链路预测算法进行对比。

1) CN 法。在给定的复杂网络或图中，给定一对节点x和y的公共邻居的规模被计算为2 个节点邻节点的交集大小，如式(3)所示。

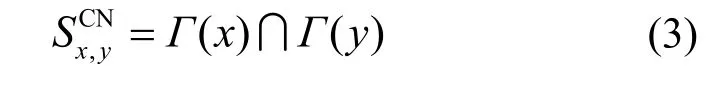
其中，Γ(x)和Γ(y)分别为节点x和y的邻居，在x和y间存在联系的可能性随着其间共有邻居的数量而增加。

2) AA 法。该方法为一种基于共享特征的相似度计算方法，并将其用于链接预测中，具体计算方法如式(4)所示。

其中，z表示节点x和y的公共邻节点，由此可知更多的权重被分配给阶数较小的公共邻节点。

3) Jaccard 系数法[6]。此度量方法与公共近邻法相同，不同之处在于，如果2 个节点有较多的公共邻点和较少的非公共邻点，则其相似度较大。在将上述相似度分数标准化后，可表示为

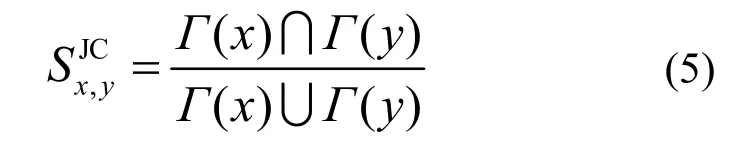
其中，Jaccard 系数被定义为从任意一个节点的所有邻节点中选择成对节点的公共邻节点的概率。

4) 优先连接（PA,preferential attachment）[9]。其将优先依附的思想用于生成一个不断增长的无标度网络中，节点度数是预测新链接的关键属性。度数越高的2 个节点在未来彼此交互的可能性越大，添加与节点x和y相关的新链接的可能性与节点度k(x)和k(y)成正比。节点x和y间的优先链接分数为

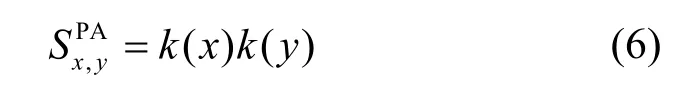
其中，节点特征值上的聚合函数可用于计算链接特征值。

5) CAR 指数[11]。基于两节点共同近邻为本地社区成员，则两节点间的链路更可能存在的假设进行设计，且会随着种子节点对间的公共近邻链路数量而增加，具体如式(7)所示。

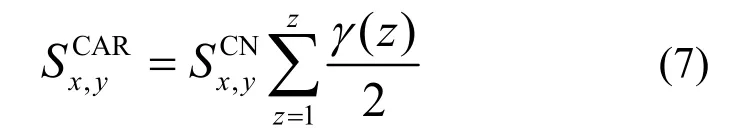
其中，γ(z)为节点邻域子集。

6) Katz 指数[10]。该指标可看作最短路径度量的改进，可直接聚集x和y间的所有路径，并对较长路径进行指数转储惩罚，具体如式(8)表示。

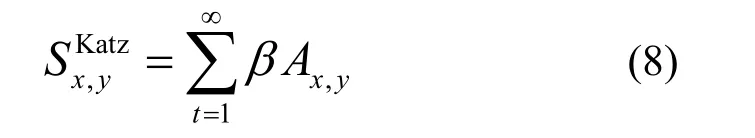
其中，β表示控制路径权重，A表示邻接矩阵。

7) 本地路径指数（LP,local path index）[6]。本地路径指数法为局部与全局链路预测方法在精度和计算复杂度间的良好折中。如x和y间没有直接联系，表示x和y间长度为n-1 的不同路径，该指数也可扩展为如式(9)所示的形式。

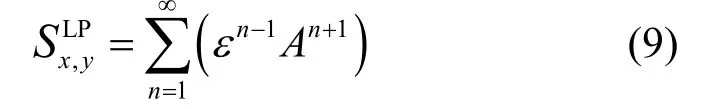
其中，n为最大阶数。

8) Node2vec（N2V）[16]是一种节点嵌入技术，学习图中节点的低维连续表示，目的是为了保持邻域结构，并将有偏随机游动作为抽样策略。其中共存在4 个参数，即行走次数（即为每个节点生成的随机游动数）、游动长度（即每次随机游动中的节点数）、返回超参数p和输入输出超参数q。

9) 扩展资源分配（ERA,extended resource allocation）[17]是一种2 个节点间通过本地路径传输的潜在资源，基于节点间的资源交换，提出了一种扩展的资源分配指标，具体如式(10)所示。

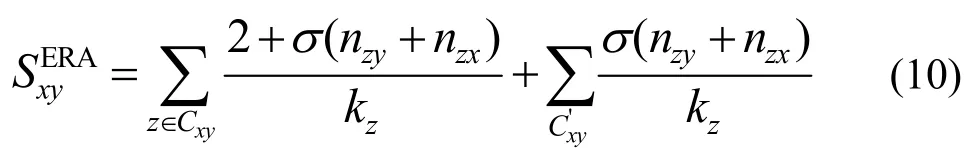
10) 资源传输容量（PIC,potential information capacity）[21]在考虑信息通道和容量的情况下，提出了信息容量的定义，用以量化节点间的信息传输能力，具体如式(11)所示。

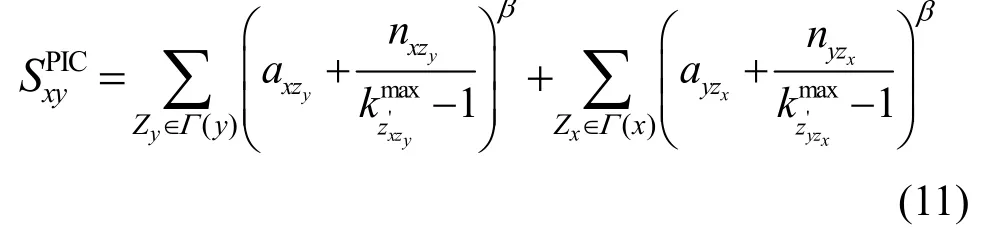
11) Propflow 指数[22]。基于流随机游走的链路算法通过将粒子的随机游走限制在有限步以内，当游走时遇到已游走过的节点或者回到原始节点则停止游走。

3.3 实验结果

本文分别在 Python 环境中使用 Scipy[11]、Numpy[6]和LPmade 工具包[13]执行上述算法和本文所提HPS-LP 法。然后利用上述评价指标，对不同的真实网络数据集进行评估，并对不同参数进行了敏感性分析。由于实验中HPS-LP 法预测列表在每次运行时的结果都有可能不同，故设置评估结果为迭代500 次运行后的平均值，运行的平均标准差为1.286。表2 为各数据集在不同方法中的曲线下面积值（其他算法的曲线下面积值都差于表中算法，故在此不再赘述）。从表2 可以看出，本文所提HPS-LP法在社交网络数据集中都具有较优的实验结果。在科研协作网络中虽然结果也较好，但不能保证最优。hep-ph 科研论文作者合作网络的聚类系数较低，故具有长度3 的路径较少，故本文所提方法在上述2 个数据集中的实验结果相对较差，而在其他聚类系数较大的网络中有较好表现。除本文所提HPS-LP 法外，LP 法与PIC 法次之，且分别在hep-ph 数据集和Twitter 数据集中具有较好表现，这是由于LP 法作为一种类局部链路预测法在非大型数据集中具有较优效果，PIC 法作为一种重视信息传输的链路预测方法在信息资源爆炸的社交网络数据集中具有较优效果。而基于CN 的链路预测算法普遍效果较差，这是由于在现今信息爆炸的状况下，受各种拓扑特征和系统动力学要素的影响，只考虑CN 并不足以涵盖预测所需的信息。

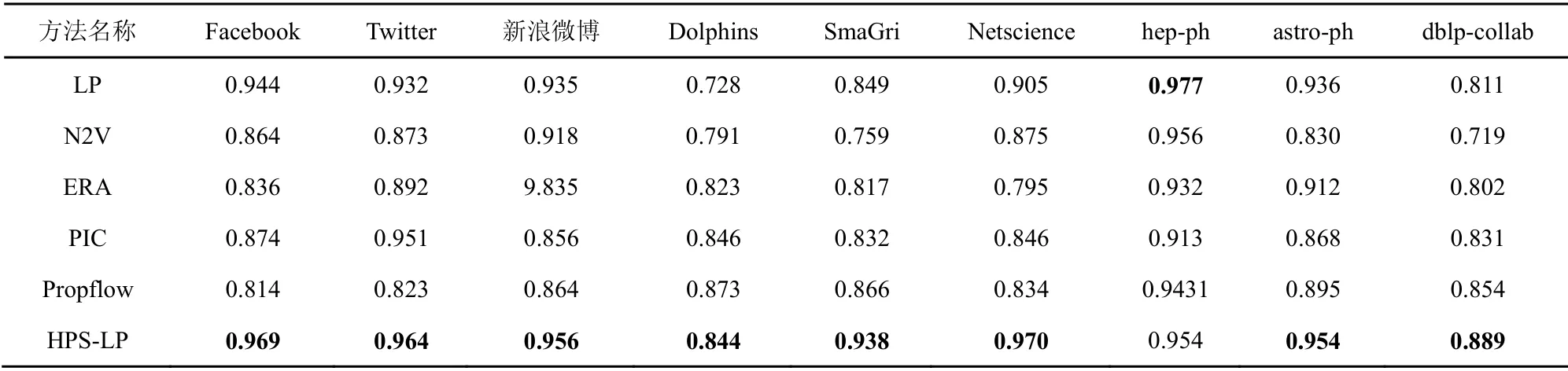
表2 各数据集在不同方法中的曲线下面积值

表3 为各数据集在不同方法中的平均精度值（其他算法的精度都差于表中算法，故在此不再赘述）。结果显示，本文所提HPS-LP 法在复杂网络数据集中具有较高的平均精度值，而在聚类系数较低的科研协作网络稀疏数据集中的平均精确度较低。除本文所提HPS-LP 法外，LP 与ERA 法的精度次之，都在科研合作网站中具有较优效果，其原因是LP 法作为一种类局部链路预测法在非大型数据集中具有较优效果；ERA 法作为一种基于节点间本地路径传输潜在资源的链路预测方法，故能有效对科研合作网络中的潜在合作链路实现预测。基于CN 的链路预测算法普遍效果较差，这是由于在信息爆炸的现状下，受各种拓扑特征和系统动力学要素的影响，CN 并不足以涵盖预测所需的信息。N2V 法作为一种节点嵌入技术，为保持邻域结构牺牲了部分预测精度，故在大型数据集中性能较差。

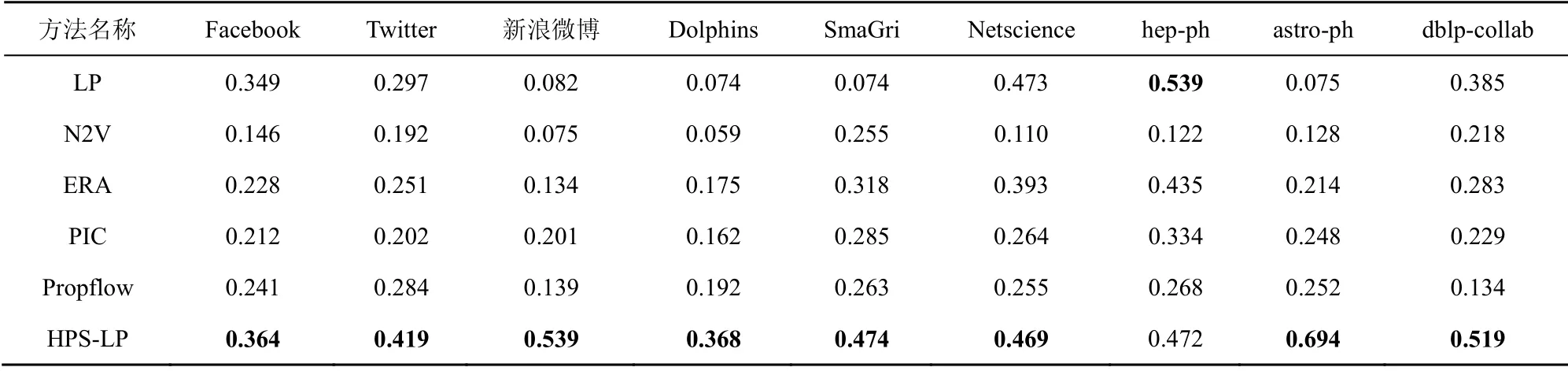
表3 各数据集在不同方法中的平均精度值

3.4 敏感性分析

针对参数值ψ的影响，本文将不同长度的路径作为特征属性来计算网络中两节点间的相似度。本文就参数值ψ在区间[0.0,1.0]范围内对曲线下面积和精度值的影响进行了分析。图1 为不同复杂网络中基于曲线下面积值的惩罚参数敏感性分析（由于其他算法的曲线下面积敏感性参数都远差于本文所提算法，故在此不再赘述）。由图1 可知，本文所提HPS-LP 法在社交网络和科研协作网络中受参数值ψ影响不显著，而LP 法受参数值ψ的稳定性仅次于HPS-LP 法。相比其他网络，链路预测方法普遍在社交网络数据集中具有更优表现。PIC 法受参数值ψ的稳定性较差，这是由于其需考虑信息通道与信息容量。

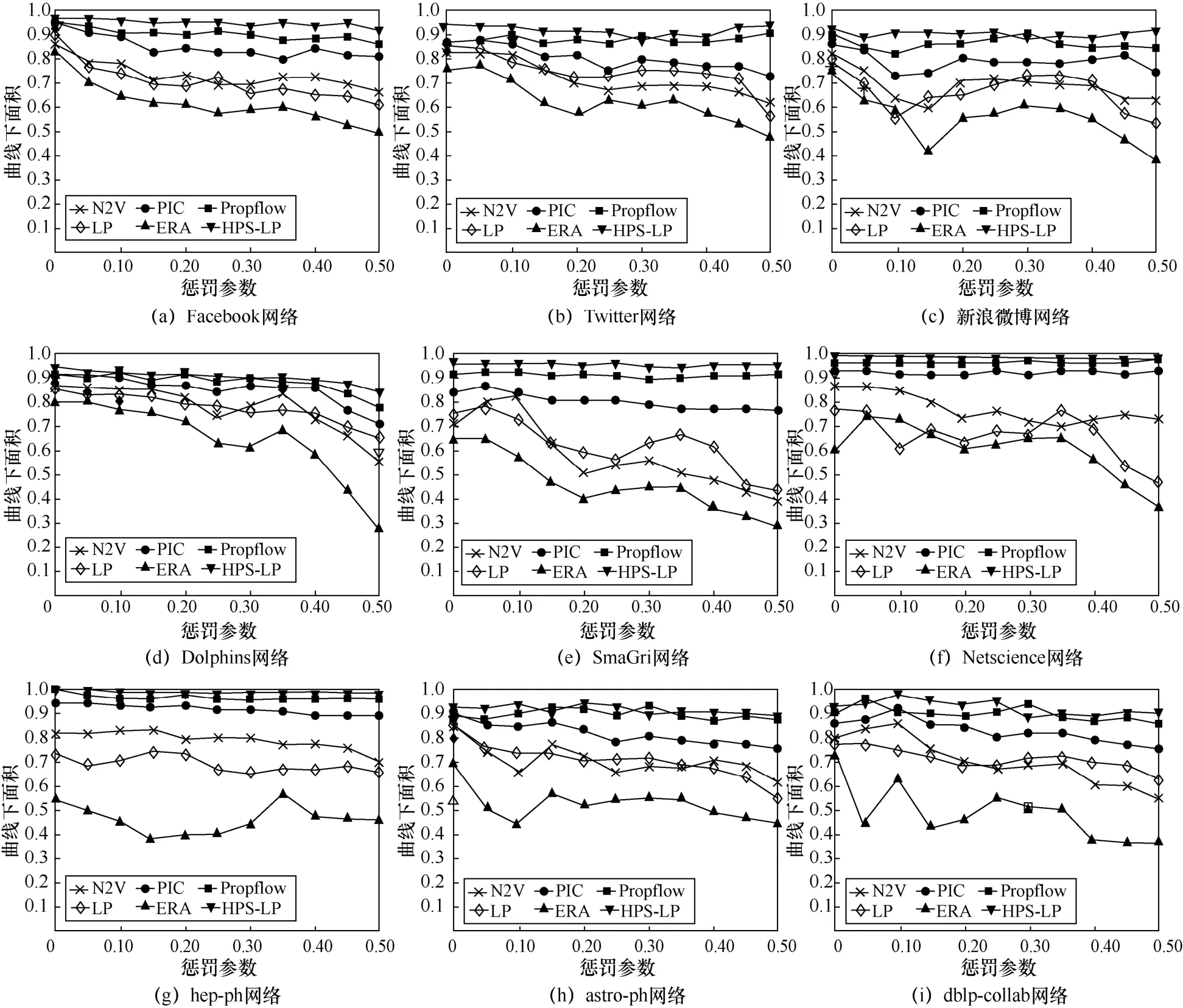
图1 不同复杂网络中曲线下面积值的惩罚参数敏感性分析

图2 为不同复杂网络中精度值的惩罚参数敏感性分析（由于其他算法的精度敏感性参数都远差于本文所提算法，故在此不再赘述）。由图2 可知，本文所提HPS-LP 法精度最高，LP 法其次。Katz法随惩罚参数值的变化较大，这本质上是由于其为一种最短路径度量方法，故预测结果存在不稳定性。相对社交网络，惩罚参数值对科研协作网络的影响较大，这是由于科研合作网络具有较低度值，故算法稳定性更高。

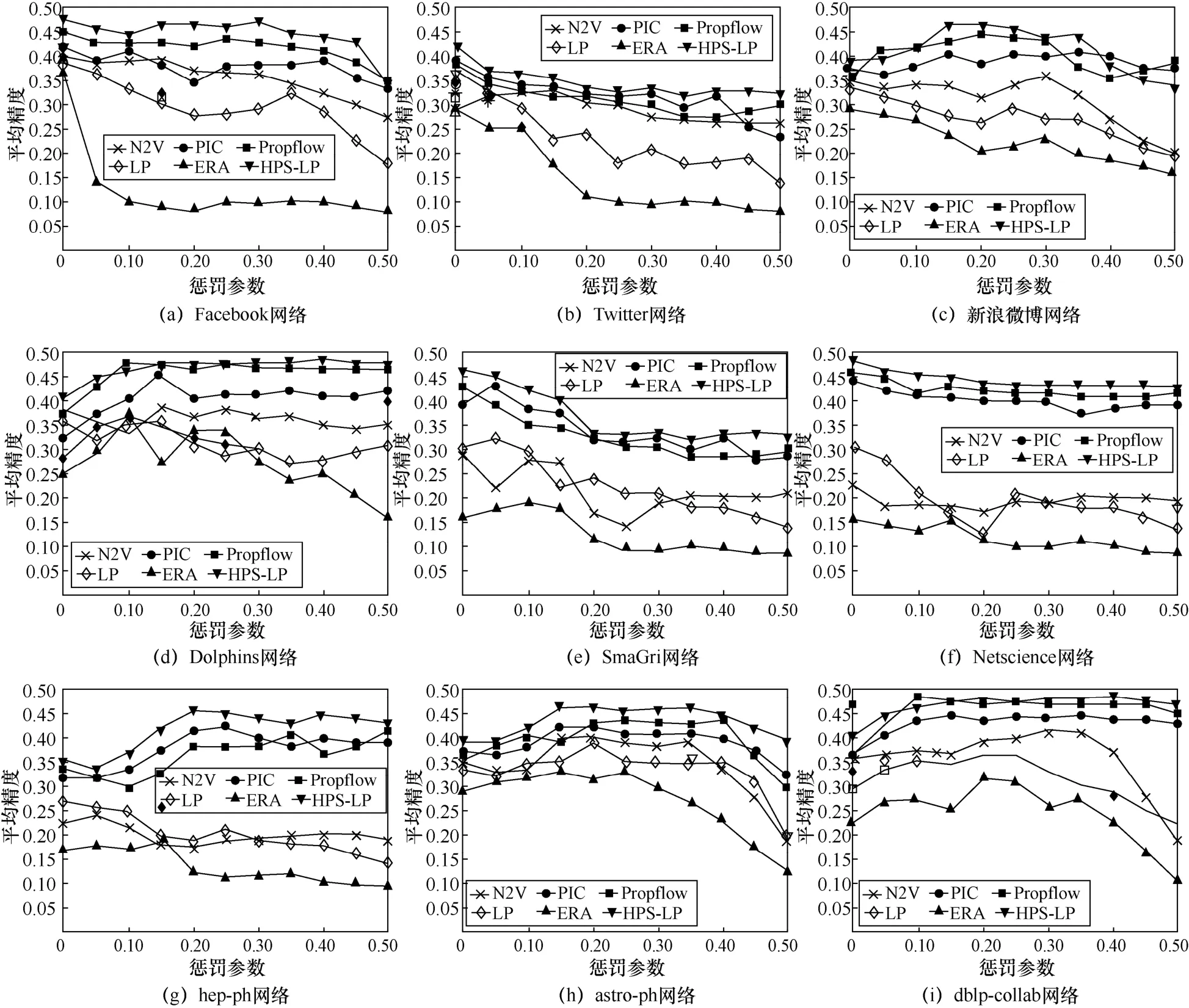
图2 不同复杂网络中精度值的惩罚参数敏感性分析

本文将路径视为特征参数之一，认为在大多数复杂网络中任何两节点间的路径平均长度为6（即六度分隔理论），故路径长度可达6。表4 为短路径(l≤ 3)与长路径(l>3)下的链路预测精度。由表4可知，社交网络中短路径和长路径的曲线下面积值值没有显著差异；科研协作网络短路径和长路径的曲线下面积值存在显著差异。当考虑较长路径时，曲线下面积值在大多数科研协作网络中甚至会降低，链路预测方法的精度没有显著提高。

表4 路径长度对链路预测精度的影响

本文基于以下假设对时间复杂度进行了讨论，即大多数复杂网络都为稀疏的，并将每个节点的平均边数设为n（网络中节点数的阶数）。最高阶路径lmax是节点对间路径最大长度，超过最高阶路径则定义认为相似性概率对高阶路径不产生影响。本文所提HPS-LP 法的关键是计算2 个及以上的路径长度分数。算法1 会循环迭代至O(n2)次，普通节点对的CN 值的成本为O(n2K)。对于阶数更高的路径，时间复杂度由2 个循环使用时间O(n2K)和O(nlgn) 组成，具有较高路径的总时间复杂度为O(n2K)+O(n2)，故本文所提HPS-LP 法的总时间复杂度为O(n2K)。基准算法的时间复杂度如文献[14]所示，在此不再赘述。时间复杂度的算法比较结果如图3 所示。

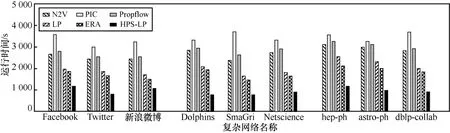
图3 时间复杂度的算法比较结果

4 结束语

复杂网络中的拓扑结构和演化会受到各种拓扑特征和系统动力学要素的制约。现有基于公共近邻的链路预测方法普遍存在效率较低、维数灾难等问题。而当今信息爆发的现状对复杂网络链路预测算法的运行效率和精度提出了更高的要求。社交关系的重要性则要求必须在链路预测算法中考虑边权重的影响。由于有关研究说明用户间的弱关系具有极高的商业价值，故对高阶路径中的链路预测及其隐私保护提出了更高的要求。故在本文所提HPS-LP 方法中，利用路径作为判别特征来预测复杂网络中的缺失链接；并以资源分配过程为目标，通过基于公共近邻的连接惩罚限制信息泄露，以最大化描述节点间相似度的节点对间的信息流。高阶路径（基于六度分隔理论）也被用作判别特征，并对其应用惩罚函数。本文在多个真实复杂网络中进行了仿真实验，结果表明所提HPS-LP 法优于基准方法，且考虑高阶路径相似度能有效提高其对复杂网络的链路预测精度，并显著影响计算时间复杂度。

尽管本文已提出了上述具有重要意义的发现，但还具有一定局限性，其中一些可能会为未来的进一步研究指明方向。首先，本文所提HPS-LP 法利用路径作为判别特征进行链路预测，故在后续研究中可结合更多具有路径复杂性的复杂网络数据集来对本文所提链路预测方法进行验证。其次，由于本文所提HPS-LP 法应用了公共近邻思想，故未来可尝试利用神经网络或探索异构动态网络嵌入技术对链路预测方法进行进一步优化，以消除可能存在的维数灾难等问题。最后，由于本文所提方法以资源分配过程为目标，故可结合社会化调查法和计算实验等研究框架，分别在有/无向图中对所提链路预测方法进行进一步佐证。