随机参数下大倾角煤层开采飞矸运动法向特征量理论
2021-08-16周一童吕文玉
刘 明,周一童,吕文玉
(1.辽宁石油化工大学 环境与安全工程学院,辽宁 抚顺 113001; 2.西安科技大学 能源学院,陕西 西安 710054)
我国大倾角煤层埋藏复杂、赋存广、资源优质,大倾角煤层走向长壁开采中顶板漏冒、煤壁片帮与割煤飞溅等所引发的飞矸灾害问题一直未能很好地解决[1]。由于大倾角煤层开采环境的复杂性,开采过程中存在诸多随机性因素,飞矸自溜性强,并且冲击力大,极易造成飞矸伤人,损坏支架,砸坏设备等事故。
虽然相关学者在飞矸灾害防护方面取得了一些研究成果,但仍需进一步加强飞矸运动全过程及防护机制等科学问题的研究[2-8]。伍永平等[9-11]运用统计学原理分析了不同工况下冲击能的演化特性,建立了飞矸损伤风险判别模型,依据模型划分了飞矸损伤等级。并从飞矸冲击能和设备冲击能恢复系数着手控制飞矸的损伤风险。郭晓伟[12]以经验公式和能量守恒理论为基础,建立了计算飞矸冲击力的简化模型,研究了不同下落高度和不同飞矸质量的最大冲击力。笔者等[13-15]基于动量矩守恒定律研究了顶板漏冒形成的飞矸与工作面底板的冲击运动规律。建立了具有不确定性参数的球形飞矸运动学特征量的区间分析模型和工作面飞矸安全评价模型。并基于动态贝叶斯网络方法对飞矸运动全过程威胁等级进行评估。准确的描述飞矸运动规律和碰撞冲击力峰值是飞矸防护机制建立的基础。根据飞矸运动轨迹和飞矸的动能可对飞矸防护装置的位置和防护能级进行设计,而防护装置的强度设计则需依据飞矸碰撞冲击力峰值来确定。现实中飞矸运动涉及多源的不确定性。首先,飞矸的形成具有不确定性,导致飞矸的尺寸和初始速度具有很大程度的不确定性。其次,飞矸及飞矸与工作面底板、煤壁、工作面行人和设备碰撞接触区的弹性模量、密度等物理参数也具有很大的不确定性。要想准确的描述飞矸的冲击运动规律,则必须要考虑飞矸运动过程中的不确定性因素。因此,笔者以飞矸与工作面底板冲击运动为例,考虑飞矸的尺寸、密度、法向冲击速度和飞矸与工作面底板碰撞接触区的弹性模量等参数的随机性,系统研究大倾角煤层开采飞矸运动法向特征量的随机特性。
1 飞矸法向最大冲击力的随机特性
大倾角煤层开采过程中顶板漏冒、煤壁片帮、架间密封不严或者移架等均会产生脱离母体的煤岩块,起初这些煤岩块处于静止状态,在采煤机甩煤、移架、推溜等扰动下脱离母体的煤岩块由静止开始运动形成飞矸。工作面飞矸现场实测发现煤岩块的产生形式有多种,如图1所示[16]。

图1 工作面飞矸灾害Fig.1 Disaster of flying gangue in working face
由于煤岩体的自然安息角小于煤层倾角,飞矸与工作面底板第1次碰撞后难以停止,将沿工作面底板滑滚或飞溅,运移过程和已停止运移的煤岩块形状表明,飞矸的棱角经过多次与底板的碰撞和滚动后磨圆的程度较好,大体呈椭球体,为便于分析,将飞矸与工作面底板的碰撞视为球体对半无限弹塑性体的冲击作用,如图2所示。假设飞矸和工作面底板为均匀弹塑性体。则飞矸的法向速度分量vn为

图2 飞矸运移方式Fig.2 Motion mode of flying gangue
vn=vcosα
(1)
式中,v为飞矸冲击速度;α为飞矸速度与工作面法向方向的夹角。
Hertz 在假设接触面是半径为a的圆的基础上,给出了2个球体在接触压力P作用下的弹性接触问题的完备解,如图3所示[17-18],图中,δ1,δ2分别为2个接触体的接触变形量;δ为总的接触变形量;r为坐标轴。

图3 Hertz 接触问题Fig.3 Hertz contact problem
接触压应力p(r)分布为

(2)
最大接触压应力Pmax位于r=0处,即

(3)
接触变形量与接触面积之间有如下关系:
a2=R*δ
(4)
其中,R*为等效半径,1/R*=1/R1+1/R2,R1和R2分别为2个半球体的半径。由于工作面底板为平面,则R2→∞,等效半径即为飞矸半径。
接触压力与变形之间的关系为
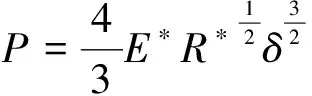
(5)
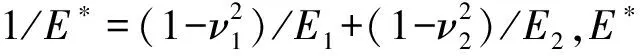
质量为m的飞矸以法向速度vn冲击工作面底板,如果在整个碰撞过程中工作面底板均处于完全弹性状态,根据能量守恒定律得到

(6)
式中,δmax为最大接触变形量。
由式(6)解得
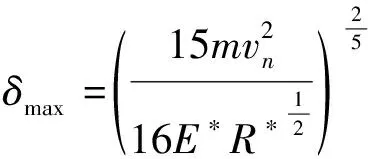
(7)
将式(7)代入式(5),可得飞矸法向最大冲击力Pmax为

(8)
式中,ρ为飞矸密度。
由于飞矸的半径、密度、法向冲击速度和等效弹性模量等参数均具有随机性,从而导致飞矸法向最大冲击力具有随机性,利用随机因子法得到

(9)
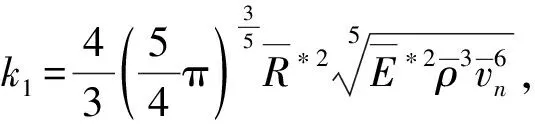
利用求解随机变量函数数字特征的代数综合法,得到飞矸法向最大冲击力的均值和方差为
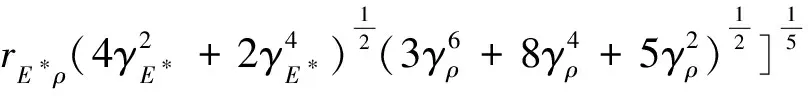
(10)
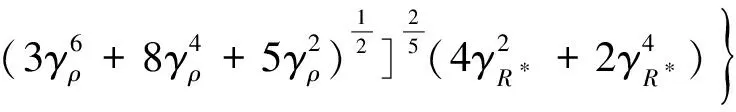
(11)
式中,μPmax,σPmax分别为飞矸法向最大冲击力的均值和方差;γE*为等效弹性模量的变异系数;γR*为等效半径的变异系数;γρ为飞矸密度的变异系数;rE*ρ为等效弹性模量和飞矸密度的相关系数;γvn为飞矸法向冲击速度的变异系数;μ和σ分别为对应随机变量的均值和方差。
2 飞矸法向碰撞恢复系数的随机特性
工作面底板实际为弹塑性材料,当最大接触应力达到工作面底板的屈服强度时,就会在接触处产生塑性变形区。令Pmax=py,a=ay,将式(4),(5)代入式(3),得到工作面底板初始屈服接触半径ay与接触面材料屈服应力py之间的关系为

(12)
使工作面底板接触区恰好发生塑性变形的飞矸临界碰撞速度为vy,此时飞矸动能全部转化为工作面底板的弹性应变能,即

(13)
将式(12)代入式(13),得到飞矸临界碰撞速度为

(14)
利用随机因子法,由式(14)得到

(15)

利用求解随机变量数字特征的代数综合法得到
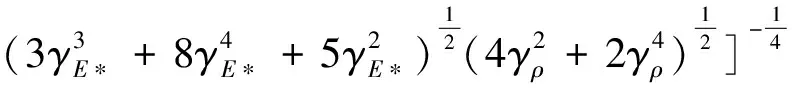
(16)

(17)
式中,μvy/vn,σvy/vn为vy/vn的均值和标准差。
Thornton以Hertz接触理论为基础,在假设材料满足理想弹塑性特性的基础上,推导了球体法向碰撞恢复系数的表达式[19]为
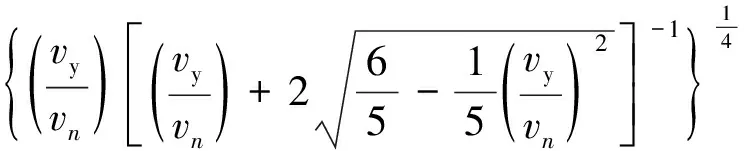
(18)
式中,en为飞矸法向碰撞恢复系数。
利用求解随机变量数字特征的矩法,得到飞矸法向碰撞恢复系数的均值μen和方差σen分别为

(19)
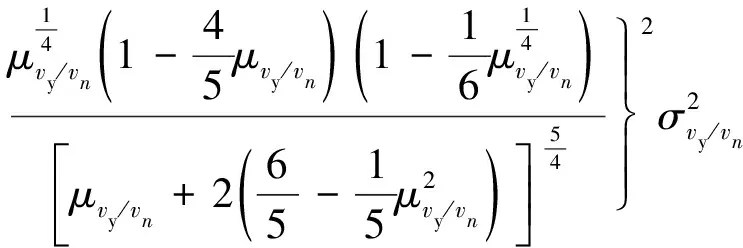
(20)
将式(16),(17)代入式(19),(20)即可得到飞矸法向碰撞恢复系数的均值和方差。
3 算 例

图4分别给出了不同随机参数对飞矸法向最大冲击力均值的影响曲线,其中all表示所有变异系数同时为随机变量,具体数据见表1。由图4(a)可知,飞矸法向最大冲击力的均值曲线总体上随着参数变异系数的增大呈现上升趋势;由于飞矸的冲击力与飞矸半径的平方成正比,飞矸半径的随机性对飞矸法向最大冲击力的均值影响最大,飞矸密度的随机性对飞矸法向最大冲击力的均值影响也较大,影响程度排序为R>ρ>E*>vn。因此,在防护装置的强度设计中应重点考虑飞矸半径和飞矸密度的影响。已知飞矸的法向冲击速度和工作面底板弹性模量的概率分布,在某一监测时间内,对已停止运移的飞矸进行收集,测得飞矸尺寸、密度和弹性模量的概率分布,便可预测飞矸冲击力峰值的概率分布,据此可对飞矸防护装置进行强度设计。由图4(b)和表1可知:随着变异系数的增大,本文方法的相对误差随之增大,最大相对误差为0.33%。

图4 法向最大冲击力μPmax的均值Fig.4 Mean of the normal maximum impact

表1 本文方法与MC法得到的法向最大冲击力均值对比Table 1 Mean of the normal maximum impact suggested method and MC method105 N
图5分别给出了不同随机参数对飞矸法向最大冲击力方差的影响曲线,具体数据见表2。由图5(a)可知,飞矸法向最大冲击力的方差曲线总体上随着参数变异系数的增大呈现上升趋势;飞矸半径的随机性对飞矸法向最大冲击力的分散性影响最大,飞矸法向冲击速度的随机性对飞矸法向最大冲击力的分散性影响也较大,影响程度排序为R>vn>ρ>E*。由图5(b)和表2可知,本文方法得到的飞矸法向最大冲击力的方差与MC法模拟的结果具有高度一致性,验证了本文方法的准确性。

表2 本文方法与MC法得到的法向最大冲击力方差对比Table 2 Variance of the normal maximum impact suggested method and MC method 107 N2

图5 法向最大冲击力的方差Fig.5 Variance of the normal maximum impact force
图6分别给出了不同随机参数对飞矸法向碰撞恢复系数均值的影响曲线,具体数据见表3。由图6(a)可知:飞矸法向碰撞恢复系数的均值曲线总体上随着参数变异系数的增大呈上升趋势;等效弹性模量对飞矸法向碰撞恢复系数的均值影响最大,飞矸密度的随机性对飞矸法向碰撞恢复系数的均值影响相对较小,由于飞矸法向碰撞恢复系数的均值表达式不含有飞矸法向冲击速度的变异系数,飞矸法向冲击速度的随机性对法向碰撞恢复系数的均值无影响,影响程度排序为E*>ρ。因此,对飞矸运动的计算和分析中应重点关注等效弹性模量和飞矸密度的影响,以便能够准确预测飞矸运动轨迹和动能,为飞矸防护装置的设计提供准确的理论依据。由图6(b)和表3可知:随着变异系数的增大,本文方法的相对误差随之增大,最大相对误差为0.02%。

表3 本文方法与MC法得到的法向碰撞恢复系数均值对比Table 3 Mean of the normal collision recovery coefficients suggested method and MC method
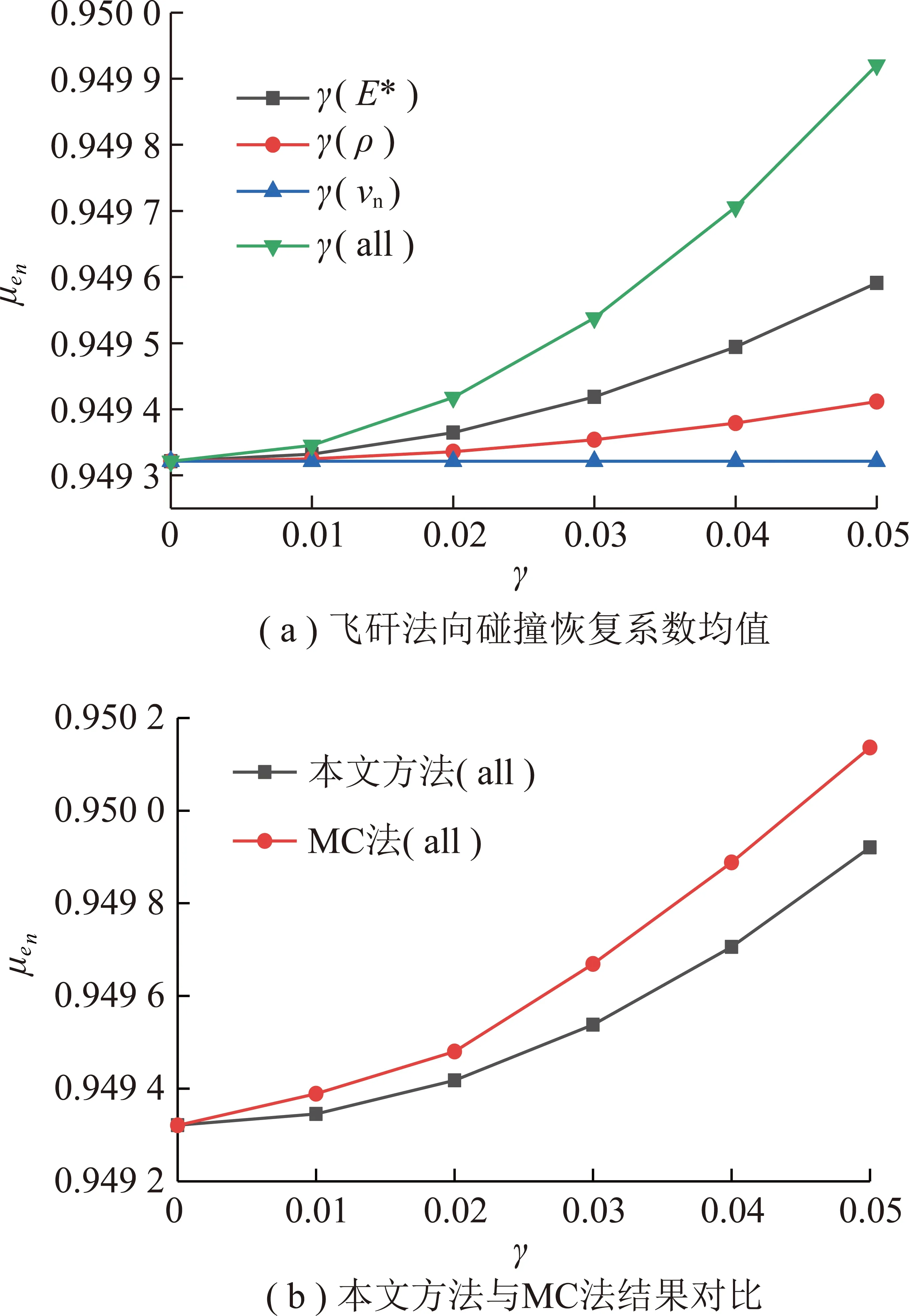
图6 法向碰撞恢复系数的均值Fig.6 Mean of the normal collision recovery coefficients
图7分别给出了不同随机参数对飞矸法向碰撞恢复系数方差的影响曲线,具体数据见表4。由图7(a)可知:飞矸法向碰撞恢复系数的方差曲线总体上随着参数变异系数的增大呈上升趋势;飞矸法向冲击速度的随机性对法向碰撞恢复系数的分散性影响最大,等效弹性模量和飞矸密度的随机性对法向碰撞恢复系数的分散性影响相对较小,影响程度排序为vn>E*>ρ。由图7(b)和表4可知:本文方法得到的飞矸法向碰撞恢复系数的方差与MC法模拟的结果也具有高度一致性,更加验证了本文方法的准确性。
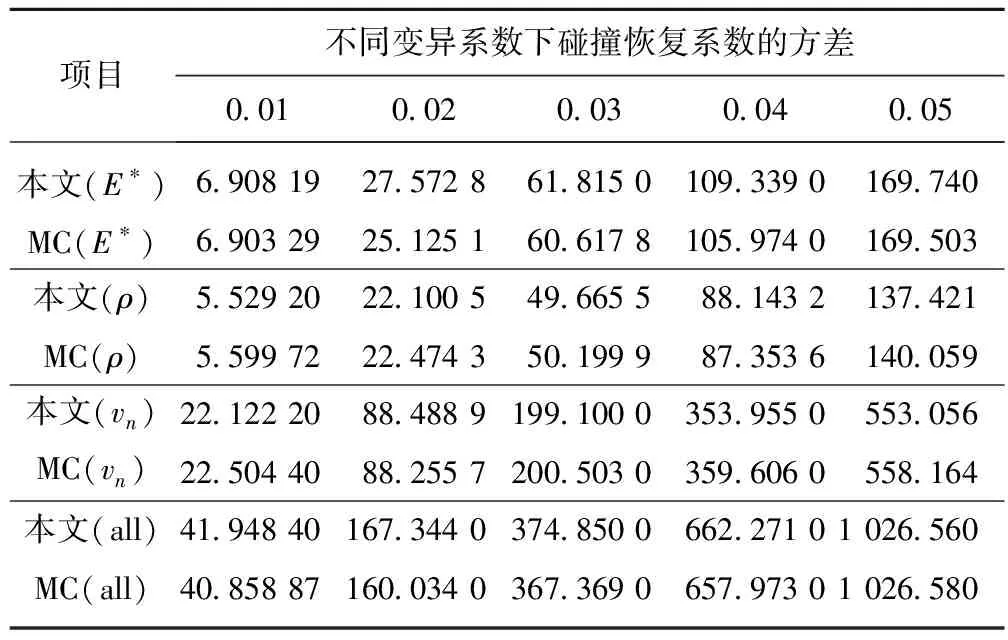
表4 本文方法与MC法得到的法向碰撞恢复系数方差对比Table 4 Variance of the normal collision recovery coefficients suggested method and MC method 10-7

图7 法向碰撞恢复系数的方差Fig.7 Variance of normal collision recovery coefficient
飞矸法向碰撞恢复系数的随机性通过影响飞矸回弹速度,进而影响飞矸冲击后的弹跳高度,弹跳高度则直接关系着飞矸防护装置的高度设置。为了分析参数的随机性对飞矸弹跳高度的影响,各随机参数的变异系数取0.02,切向碰撞恢复系数取0.85时,采用RocFall软件模拟100次得到飞矸弹跳高度的均值曲线[20],如图8所示。由图8可知,参数随机性对
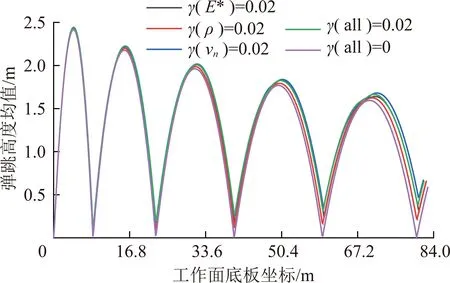
图8 飞矸弹跳高度的均值Fig.8 Mean of rebound height for flying gangue
飞矸弹跳高度均值影响较大。初始阶段参数随机性对飞矸弹跳高度的均值影响较小,随着碰撞次数的增加,参数的随机性对飞矸弹跳高度均值的影响逐渐增大。飞矸弹跳高度的随机性将导致飞矸运动轨迹也具有随机性。
4 结 论
(1)飞矸冲击运动参数的随机性对飞矸运动法向特征量的均值均有不同程度的影响。飞矸法向碰撞恢复系数的随机性,将导致飞矸弹跳高度的随机性,进而影响飞矸运动轨迹。飞矸法向最大冲击力和飞矸法向碰撞恢复系数的数字特征曲线总体上随着参数变异系数的增大均呈现上升趋势。
(2)本文方法对顶板漏冒、煤壁片帮、割煤飞溅等任意方式形成的球形飞矸对工作面底板、煤壁以及工作面作业人员和设备的碰撞也同样适用,实际计算中只需将工作面底板的弹性模量和半径等随机参数的数字特征替换成煤壁、工作面作业人员和设备等碰撞部位随机参数的数字特征。
(3)本文假设各随机参数均服从正态分布特征,对于飞矸及飞矸与工作面底板的碰撞接触区岩性没有限制,计算时只取其参数的概率统计值。因此,无论各向同性材料,还是各向异性材料都同样适用。
(4)准确的描述飞矸运动特征量是飞矸灾害预测与防护装置设计的基础。根据飞矸形成位置,以及飞矸运动轨迹特征,可确定飞矸治理原则为:“上部飞矸着重轨迹阻拦、中部飞矸强调源头治理、下部飞矸防止衍生二次灾害”。工作面下部是飞矸防治的核心区域,应加强防护等级。
