高原环境下矿井最低排尘风速的数值模拟
2021-08-16张国梁蒋仲安姚尚辉王亚朋
张国梁,蒋仲安,杨 斌,2,姚尚辉,彭 亚,王亚朋
(1.北京科技大学 土木与资源工程学院,北京 100083; 2.中国安全生产科学研究院,北京 100029; 3.西藏华泰龙矿业开发有限公司,西藏 拉萨 850212)
我国西部高海拔地区蕴含着丰富的矿产资源,具有重要开采价值。但随着海拔上升,低压低氧、寒冷干燥的气候特点会给矿井开采带来新的挑战,其中粉尘的有效控制就是问题之一[1-6]。目前井下采用的防尘措施主要是通风排尘,其关键参数是排尘风速的确定,即采用合适的风速将空气中悬浮的细微矿尘稀释并排出,降低空气中的粉尘质量浓度。
受地理环境的限制,国内外学者对高原环境下矿井通风及粉尘运动研究较少。特别是国外由于高海拔矿井数量较少,研究主要基于普通环境下的粉尘颗粒在不同流场的运动、扩散以及影响因素等。KANAOKA对施工隧道内的风流流动、粉尘质量浓度分布和颗粒运动进行模拟计算,研究了气流速度、风管结构和颗粒尺寸对通风效果的影响[7]。CANTERO研究得到二维情况下粉尘颗粒的惯性对粉尘沉积的动力学过程影响[8]。BHASKAR通过研究风流中尘粒的碰撞、沉降、扩散、二次飞扬和弥散等作用规律,建立了一维稳态均匀流动情况下的粉尘对流扩散方程[9]。国内学者对粉尘扩散的研究最初主要采用理论推导和实验分析的方法,涂继正、暨朝颂等在流体力学的基础上对井巷风流特征和粉尘受力情况进行分析,推导出了合理的排尘风速,并沿用至今[10-12]。随着CFD技术的发展,数值模拟的方法逐渐被推广到矿井粉尘扩散运动的研究中,蒋仲安、陈举师等[13-19]通过数值模拟的方法研究了破碎硐室、巷道型采场以及施工隧道等的粉尘质量浓度分布规律。由于西部高原地区的交通需求,我国逐步兴建了许多高原隧道,如正在施工的川藏铁路,并对高海拔隧道通风以及除尘进行了一定研究。曹正卯等[20-21]对不同海拔隧道内有害气体和粉尘的运移特性和浓度分布进行了数值模拟分析。从国内外的研究成果综合来看,对于粉尘运移的研究主要集中于平原地区的矿井和隧道,基于高原环境下的研究较少。但随着海拔上升,空气压力、温度和密度的降低,粉尘运移规律会发生显著改变,所以确定合理的排尘风速具有重要意义[22]。
笔者通过对不同海拔高度下掘进工作面粉尘运移规律的模拟研究,探寻工作面粉尘粒径分布特征,并与建立的排尘风速理论模型对比,得出了不同海拔掘进工作面最低排尘风速。
1 排尘风速理论模型
1.1 粒子在紊流中的运动方程
矿尘在静止空气中受外力作用(浮力、重力、电场力和其他力)的运动微分方程为
(1)
式中,m,v,t分别为矿尘粒子的质量,运动速度和时间,kg,m/s,s;Fg为粒子的重力,N;Ff为粒子在空气中受到的浮力,N;Fd(v)为粒子由于运动受到的空气阻力,N。
根据Stokes定律,当雷诺数较小时,球形粒子受到的阻力为Fd(v)=6πμrv,其中,μ为空气动力黏性系数;r为粒子半径。由于粒子密度ρp远大于空气密度ρg,导致作用于粒子上的重力远大于浮力,所以可以忽略Ff,粒子的微分方程可改写为
dv/dt=g-v/η
(2)
式中,η为张弛时间,η=m/(6πμrv);g为重力加速度。
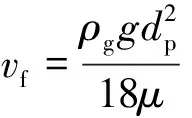
(3)
井下风流都处于紊流状态,矿尘运动时,除了受纵向风流影响,还受紊流横向脉动速度的影响。若除气流推动力和空气阻力外,只有重力和浮力作用于粒子时,巷道中粉尘粒子的运动微分方程为

(4)
式中,u1,v1为风流和矿尘沿巷道方向的速度,m/s;u2,v2为风流和矿尘沿巷道截面的脉动速度,m/s。
由于ρp≫ρg,可以忽略浮力Ff,并对方程进行化解,得到粒子沿水平方向和竖直方向的微分方程写为
dvx/dt=(u1-v1)/η
(5)
dvy/dt=g+(u2-v2)/η
(6)
对微分方程进行求解,得到vx,vy:
vx=u1-(u1-v1)e-t/η
(7)
vy=u2-(u2-v2)e-t/η-vf
(8)
但对于细微的矿尘颗粒,(u1-v1)e-t/η≈0,(u2-v2)e-t/η≈0,所以式(7)和(8)可以化解得到:vx=u1,vy=u2-vf。
1.2 最低排尘风速的理论模型构建

根据圆管定常湍流可知,靠近管壁处,流动呈层流状态,雷诺数较小,黏性切应力τw占主要地位,雷诺应力τt可忽略不计,即紊流切应力τ0为

(9)


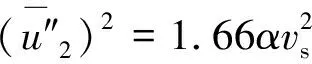
(10)

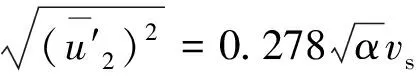
(11)

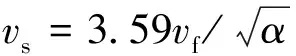
(12)
对于金属矿山,规程规定:硐室型采场的最低排尘风速不小于0.15 m/s,巷道型采场和掘进工作面不小于0.25 m/s。研究得到在该风速和扰动气流的共同作用下,能将10 μm以内的大部分颗粒悬浮于空气中并随风流动,达到排尘的目的。但此风速是基于平原矿井研究得到的结果,当海拔大幅上升后,α会明显降低,若仍采用上述规定,不进行修正,井下粉尘质量浓度势必将会增大,从而影响人员健康和机械设备的运转。
根据紊流状态下的摩擦阻力定律得到,巷道摩擦阻力因数α为λρ/8,其中,λ为沿程阻力系数,通过实验可确定;ρ为空气密度。对于固定巷道,其巷道支护形式和尺寸确定,λ就确定,所以α只与ρ成正比。而在高海拔地区,空气密度会明显下降,在甲玛矿海拔4 500 m平硐处测得的空气密度只有0.74 kg/m3,约为海平面的60%。所以在计算高海拔矿井摩擦阻力因数时,需要添加密度修正参数k,如下式:
α=α0ρ/1.293=kα0
(13)
式中,α0为标准状态下的摩擦阻力因数,(N·s2)/m4;k为修正系数。
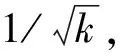
2 几何模型的建立和求解
2.1 几何模型和网格划分
以西藏甲玛矿4490分层6号探矿巷为研究背景,建立几何模型。为了得到可靠的模拟结果,建立的几何模型必须符合现场情况,但工作面还存在许多其他工艺流程,完全复制现场细节较难,且其他设施和活动对模拟结果影响较小。因此,综合考虑计算机性能和模拟精度等因素,对模型进行简化处理。
采用SoildWorks按1∶1建立掘进工作面通风模型,如图1所示。其中巷道截面为三心拱,尺寸为60.0 m×4.2 m×3.7 m(长×宽×高),采用压入式通风系统为工作面供风,风筒悬挂于巷道右侧,直径0.6 m,距地面1.4 m。将建好的模型导入Workbench中,采用Design Modeler进行Boolean运算,并划分网格,如图1所示。
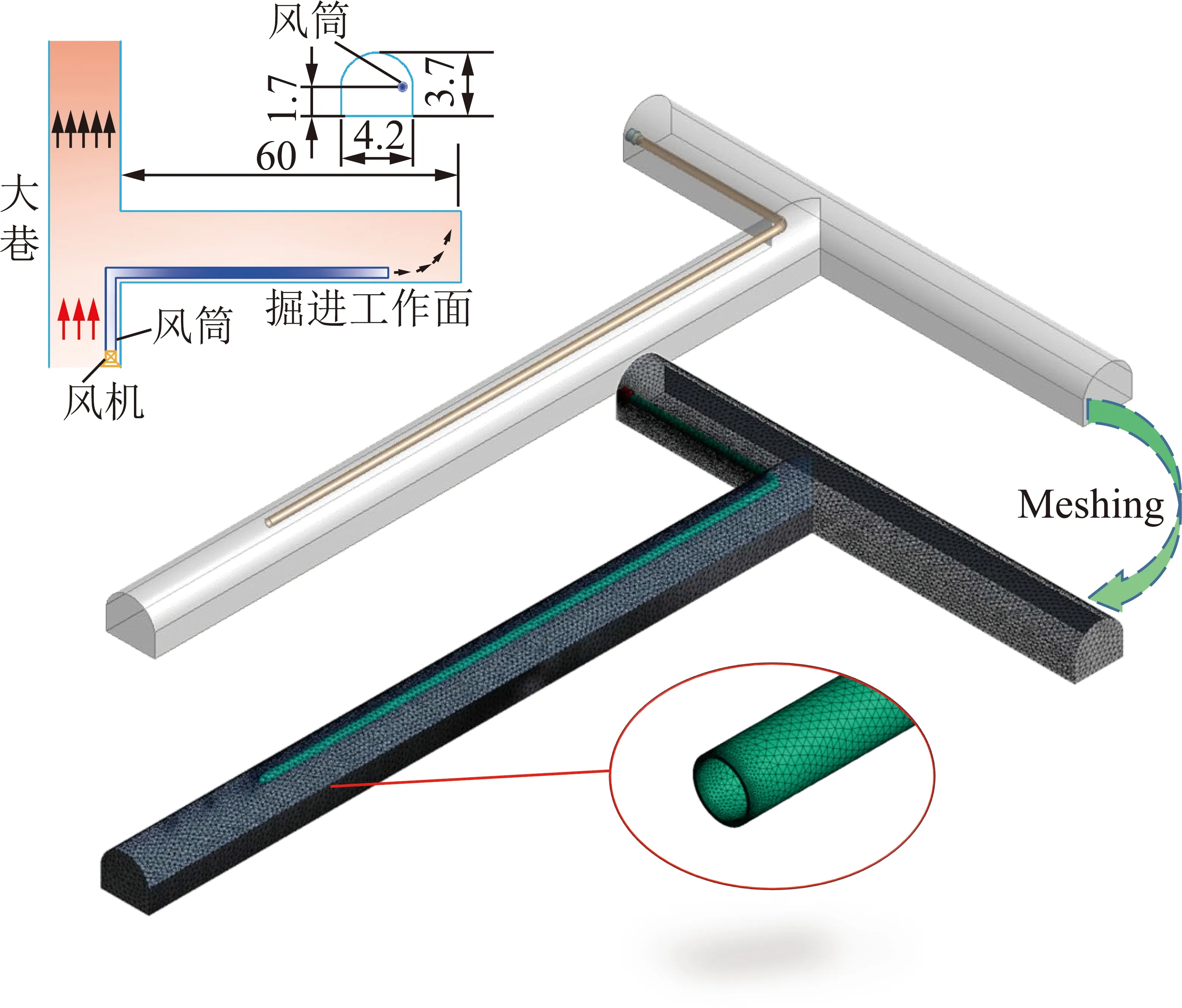
图1 掘进工作面几何模型和网格划分Fig.1 Geometric model and meshing diagram of driving face
2.2 网格独立性验证
在数值模拟分析中,网格独立性验证对模拟结果非常重要。在研究不同风速下粉尘扩散运动时,气流是影响模拟结果的主要载体,因此风速被设定为网格独立性验证的主要参数。利用Meshing对模型进行网格划分,得到3种不同的网格划分方案,即方案1(259 175),2(390 217),3(860 217)。针对3种不同的方案,分别进行模拟验证,结果如图2所示。由图2可知,虽然3种方案划分的网格数量存在明显不同,但其模拟结果差异性较小。因此,满足独立性验证。考虑到计算机性能和模拟误差,采用方案2划分网格;其中平均网格质量为0.88,最大为1.00,最小为0.76。

图2 不同网格划分方法的沿程风速变化Fig.2 Wind speed variation along different meshes
2.3 计算模型的参数设定
通过查阅相关的掘进工作面污染物颗粒运移文献和资料,结合甲玛矿实际情况,根据Fluent中湍流和离散型模型的设定要求,对模型边界条件和求解参数进行设置,得出在不同海拔高度和不同风速下粉尘颗粒的运动情况。并采用CFD-post和Origin对模拟结果进行处理和分析,得出掘进工作面的流场分布,粉尘颗粒的运动轨迹和粉尘质量浓度的空间分布。具体参数设置见表1。

表1 计算模型参数设定Table 1 Calculate model parameters setting
3 数值模拟结果及分析
3.1 风流流场分析
根据甲玛矿4490分层6号探矿巷的具体情况,模拟压入式通风条件下的工作面流场分布。现场测得的大气压力、空气密度和动力黏度分别为54 027 Pa,0.73 m3/kg,1.65 Pa·s。其中压入式风机风量为204 m3/min,大巷风速为0.5 m/s,模拟得到的工作面风流流线和风速体如图3所示。由图3可知:
(1)风筒出口位置形成的射流会与边界层气体发生动量交换,形成锥形气流场;由于能量守恒,随着射流带动的边界层扰动气流增多,射流半径会扩大,风速也逐渐衰减。
(2)由于风筒位于右上角,风流到达掘进工作面后,在壁面阻碍作用下发生折返运动,形成回流区。在掘进工作面到风筒出口区域,反射气流会与射流相遇,发生冲击、掺混和整合,使流场极为混乱,并在掘进工作面附近形成逆时针旋转的涡流区域。
(3)在掘进工作面附近由于存在风流之间的冲撞,风速分布极不均匀;但继续向前运动,风速的极差值会逐渐减小,流场分布逐渐均匀,最终稳定在0.25 m/s左右,如图3所示(其中,Z为至掘进工作面距离)。
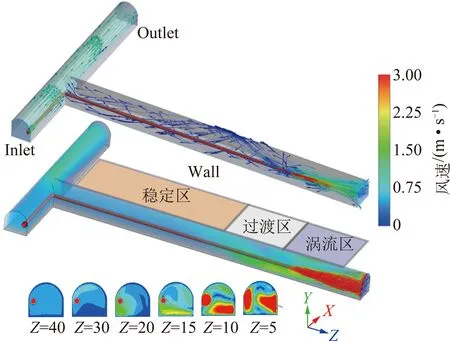
图3 掘进工作面空间流线分布和风速体Fig.3 Spatial streamline distribution and wind speed body of driving face
3.2 不同粒径的粉尘运动情况分析
在压入式流场模拟的基础上,模拟高原环境下的粉尘扩散。采用离散型模型,在掘进工作面设置喷射源,颗粒粒径满足R-R分布,其中颗粒的最小粒径为1 μm,最大为39 μm。模拟得到不同粒径的颗粒随时间的运动轨迹如图4所示,由图4可知。
图4 颗粒随时间的运动轨迹Fig.4 Particle trajectory over time
(1)粉尘颗粒由掘进工作面产生后,在压入式风流的作用下,向前扩散。粒径较大的颗粒在重力作用下,在掘进工作面附近沉降;而小颗粒在湍流脉动速度的作用下继续悬浮于空气中,随风流向前扩散。在扩散过程中,颗粒沉降到地面会被吸附而终止运动。
(2)粉尘颗粒越大,沉降时间越短,最终沉降速度就越大。掘进工作面粉尘向前扩散的过程中,随着大颗粒的逐渐沉降,风流中携带的粉尘以15 μm以下的颗粒为主,且数量越来越少。
(3)掘进工作面附近存在涡流,风速不均匀,导致粉尘扩散速度较快;但继续向前运动,颗粒数量在减少,扩散速度也在逐渐降低。粉尘自掘进工作面扩散到风筒出口(13 m)约需30 s,扩散到工作面入口(60 m)约需150 s,扩散到模型出口(85 m)需要210 s。
粉尘颗粒扩散到大巷后,由于存在风流汇合,扩散速度会加快,在210 s左右达到稳态,即颗粒由工作面产生,经大巷排入专用回风巷,其中部分颗粒沉降于地面而停止运动。达到稳态后,不同粒径的颗粒扩散轨迹如图5所示。由图5可知,颗粒粒径越大,扩散距离越短,扩散范围越小;15 μm及15 μm以下的颗粒一部分经大巷排出,一部分沉降于地面,而15 μm以上的颗粒在掘进工作面附近就会全部沉降。

图5 不同粒径的颗粒扩散轨迹Fig.5 Particle diffusion trajectories of different particle sizes
在海拔4 490 m,工作面风速0.25 m/s的环境下,粉尘扩散过程中,除了大颗粒发生沉降,很多小颗粒也沉降到了地面,包括呼吸性粉尘。所以对于高海拔环境,规程规定的掘进工作面最低排尘风速难以将对人体危害较大的呼尘全部带走,需要基于高原环境对最低排尘风速进行优化修正。
3.3 不同海拔高度对粉尘扩散的影响
由前面的模拟结果可知,海拔上升会对粉尘颗粒的运动产生影响,特别是粒径较小的颗粒。为了观察不同海拔高度对粉尘运动的具体影响,选取t=210 s时,对掘进工作面空间粉尘质量浓度进行分析,此时粉尘质量浓度分布达到稳定状态,具有代表性。沿粉尘运动轨迹截取距离掘进工作面X=5,10,15,20,25,30,35,40,45,50,55 m共11个截面,对其平均粉尘质量浓度进行分析。分别模拟在0.25 m/s的排尘风速下,海拔0,2 000,4 000,6 000和8 000 m环境不同截面粉尘质量浓度的变化趋势,其中不同海拔的参数设置见表2,模拟结果如图6所示,由图6可知:
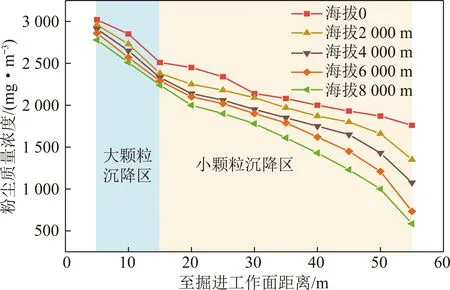
图6 各海拔高度不同断面的平均粉尘质量浓度变化趋势Fig.6 Trend of average dust concentration in different sections at different altitudes

表2 不同海拔的环境参数Table 2 Environmental parameters at different elevations
(1)粉尘在向前运动的过程中,随着距离的增加,颗粒不断沉降,沿程粉尘质量浓度不断降低。在掘进工作面附近,由于大颗粒的快速沉降,粉尘质量浓度下降迅速;而小颗粒在风流的携带下,沉降缓慢;前5~15 m的沉降率约为18.9%,从15~55 m的沉降率最低为24.21%,最高达53.18%,所以在掘进工作面附近存在一个粉尘质量浓度变化的转折点。
(2)海拔升高,颗粒沉降速度逐渐增大,同一截面位置的粉尘质量浓度越来越低,且离工作面距离越远,下降趋势越明显。在大颗粒沉降区,不同海拔粉尘质量浓度变化趋势近乎平行,这是由于空气密度降低对大颗粒的影响较小;而在小颗粒沉降区,粒子受空气密度的影响较大,粉尘质量浓度随海拔的下降幅度越来越明显。
为了探究海拔高度对不同粒径颗粒运动情况的影响,在工作面粉尘质量浓度达到稳定状态后,对不同位置的粉尘粒径分布进行分析。模拟计算前设定的尘源粒径的频度分布f(Dp)和和筛下累积G(Dp)如图7所示,粉尘颗粒粒径主要集中在1~39 μm,特征粒径De为12 μm,分布指数为1.98。

图7 掘进工作面粉尘粒径分布Fig.7 Particle size distribution of palm flour dust
在靠近掘进工作面尘源附近位置,不同海拔高度的空间粉尘粒径分布相似,在距离掘进工作面5 m处的截面粒径分布如图8(a)所示。而沿粉尘运动轨迹继续向前,同一位置不同海拔高度的粒径分布和质量流率差别逐渐增大,在工作面出口位置(X=55 m),不同海拔高度的截面粒径分布和质量流率如图8(b)~(f)所示,从图8可以看出:

图8 不同海拔高度的断面粉尘粒径分布Fig.8 Particle size distribution of section at different altitudes
(1)在掘进工作面附近大颗粒粉尘尚未完全沉降,所以其粒径分布与模型设定的粒径分布相似,大颗粒粉尘占比较大。但随着继续向前运动,粉尘颗粒充分弥散到风流中,大颗粒沉降到地面被吸收,导致粒径分布范围变窄,R-R分布指数增大;在工作面出口位置,6 μm以上的大颗粒基本都沉降到地面。
(2)在工作面出口位置,随着海拔升高,粉尘质量流率不断下降。在海拔0,2 000,4 000,6 000和8 000 m环境下,粉尘质量流率从23.97分别下降至21.93,18.41,11.96及10.00 g/s;从X=5 m到X=55 m截面,不同海拔高度的沉降率也由42.10%增大为47.03%,55.53%,71.11%及75.85%。
由模拟结果可知,海拔上升会加速粉尘颗粒的沉降,特别是呼吸性粉尘;但当遇到扰动气流时,沉降的小颗粒会再次飞扬,污染工作面,所以海拔高度上升会导致呼尘排出工作面的难度增加。
3.4 不同风速呼尘扩散分析及模拟结果验证
工作面通风排尘的主要目的是将对人体危害性较大的粉尘颗粒(呼尘)带走。通过前面对不同粒径的粉尘颗粒扩散分析可知,在海拔4 490 m的环境下,当vs=0.25 m/s时,风流难以将所有的呼吸性粉尘携带排出工作面。所以为了降低工作面呼尘质量浓度,减少对作业人员的危害,特对不同风速下,呼吸性粉尘的扩散轨迹进行分析。设定粒径分布指数n为2.5,特殊粒径De为3 μm,控制其他条件不变,改变工作面风速,得到的呼吸性粉尘扩散轨迹如图9所示,由图9可知:
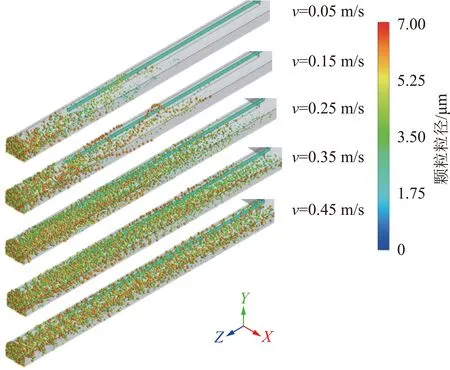
图9 不同风速下呼尘的扩散运动轨迹Fig.9 Diffusion trajectories of exhaled dust at different wind speeds
(1)掘进工作面风速越大,呼吸性粉尘扩散范围越远,沉降颗粒越少。当风速较小时,湍流脉动速度作用力不足以平衡粒子重力,掘进工作面产生的粉尘会逐渐沉降于地面而停止运动,存在二次飞扬的可能;当风速较大时,在湍流作用下,粒子在竖直方向受力平衡,能随风流排出工作面。
(2)当vs≥0.35 m/s时,大部分呼吸性粉尘颗粒能随风流排入大巷,与规定的0.25 m/s相比,vs增大了40%。测得甲玛矿4490分层6号探矿巷的空气密度为0.73 kg/m3,根据式(12)和(13),计算得到的排尘风速为0.33 m/s,与模拟结果值接近。
根据规定的粉尘质量浓度测定方法,在甲玛矿4490分层6号探矿巷布置测点,进行现场测定。通过理论模型计算得到的海拔4 490 m环境下排尘风速为0.33 m/s,调节掘进工作面压入式风机风量为287 m3/min,采用滤膜法测定轴线1.5 m高度的呼吸性粉尘质量浓度。将实测结果与风速为0.35 m/s时的模拟结果进行对比,如图10所示。由图10可知:模拟结果与实测值的变化规律相近,但在靠近掘进工作面位置,实测质量浓度较大,这是由于爆破后尚未清理的爆堆中含有的粉尘较多,导致掘进工作面附近实测的粉尘质量浓度较高。通过对比分析,说明模拟得到的排尘风速可有效降低工作面粉尘质量浓度,可用于不同海拔最低排尘风速的确定。
3.5 不同海拔最低排尘风速的确定
为了得到各海拔高度下的最低排尘风速,在尘源位置只设置呼吸性粉尘,通过改变风机风量,得到在不同风速下,工作面的粉尘质量浓度变化。在海拔0,2 000,4 000,6 000和8 000 m环境下,工作面不同风速的截面平均质量浓度如图11所示,由图11可知:
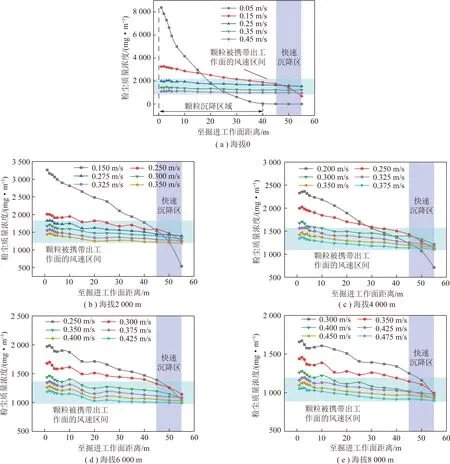
图11 不同风速下各海拔高度的断面粉尘质量浓度变化Fig.11 Changes of dust concentration at different altitudes under different wind speeds
(1)粒子运动过程中会发生沉降,距离掘进工作面越远,粉尘质量浓度越低,在靠近出口位置存在一个快速沉降区;且风速越小,粉尘质量浓度下降越快,沉降率越高,二次飞扬的可能性就越大。(2)在不同风速下,工作面粉尘质量浓度分布呈3种状态:全部沉降、部分沉降、稳定悬浮流出。即当风速较小时,粉尘在工作面会全部沉降,如在海拔0、风速为0.05 m/s环境下;当风速增大后,粉尘颗粒一部分排出工作面,一部分沉降;当风速达到一定值后,粉尘能全部随风流悬浮排出工作面。
在考虑海拔高度的影响下,能将大部分呼吸性粉尘颗粒排出工作面的最低风速即为高原环境下最低排尘风速。根据模拟结果可以看出,在海拔0,2 000,4 000,6 000和8 000 m环境下,其最低排尘风速约为0.250,0.275,0.325,0.375和0.425 m/s时,能较好的达到工作面通风除尘效果。
4 理论模型与模拟结果对比
为了确定得到的理论模型的可靠性,将不同海拔条件下理论模型的计算结果与模拟结果进行比较分析。结果如图12所示,误差值均在3%以下,得到的理论模型与模拟结果吻合,可用于指导不同海拔最低排尘风速的确定。根据得到的理论模型对不同海拔排尘风速进行修正,通过计算得到的修正系数K和最低排尘风速见表3。

图12 不同海拔理论值与模拟值的对比Fig.12 Comparison of theoretical and simulated values of different altitudes
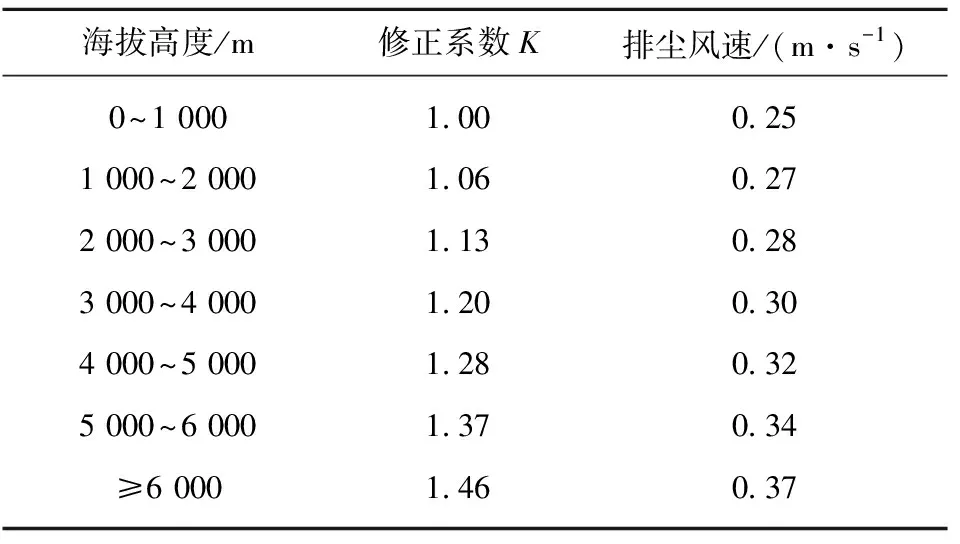
表3 不同海拔的最低排尘风速Table 3 Minimum dust velocity at different altitudes
5 结 论
(1)海拔上升,环境参数变化,为了使小颗粒粉尘能悬浮于空气中随风流动,在巷道粒子运动微分方程和湍流脉动速度特性的基础上,建立最低排尘风速的理论模型。
(2)在掘进工作面附近,风筒射流与边界层气体发生动量交换,形成锥形气流场;同时,在壁面阻碍作用下,在另一侧形成回流,2股气流冲击、掺混,形成涡流,使掘进工作面附近流场混乱;但继续向前,风速极差值减小,流场分布会逐渐均匀。
(3)海拔上升会对颗粒运动产生影响,特别是粒径较小的颗粒,其中颗粒沉降速度增大,出口位置质量流率下降;在向前运动的过程中,除了大颗粒,小颗粒也逐渐沉降于地面而停止运动,导致0.25 m/s的风速难以将呼尘全部排出工作面。
(4)模拟得到各海拔环境下风速为0.250,0.275,0.325,0.375和0.425 m/s时,能较好的达到工作面通风除尘效果;并将模拟结果与理论模型进行比较,基本吻合,误差值在3%以下。
