q分量三阶混料中心多项式模型R-最优设计

郑 婷

(兰州财经大学 统计学院， 甘肃 兰州 730030)

0 引 言

混料试验设计与工农业生产及科学实验密切相关，发展十分迅速[1].在q分量混料系统中，所度量的响应只是出现在混料中各种成份比例x1,x2,…xq的函数，而与混料的总量无关，混料问题中的各成份比例，即每种成份在混料总量中所占的百分比是不能任意变化的，要受到约束条件

的限制，从而构成了混料系统中的q-1维正规单纯形

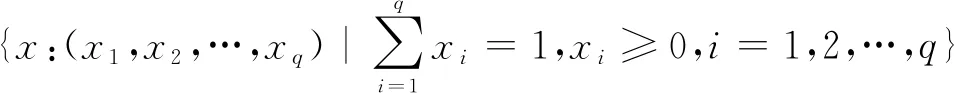
(1)

在混料试验设计中，关于D-最优设计的研究已趋于完备.D-最优准则的几何意义是最小化模型参数向量的置信椭球体的体积，但当模型参数的维数较大时，该置信椭球体的体积不易计算且解释也不够简洁明了，对此，Holger[2]基于Bonferroni-t区间法

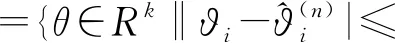
(2)

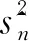
(3)

其中，(M-1(ξ))ii表示信息矩阵的逆矩阵的主对角线元素，R-最优设计的统计意义是将信息矩阵的逆矩阵的主对角线元素的乘积最小化，从而使得其矩形置信区域的体积最小.

Holger根据线性回归模型参数联合估计的Bonferroni-t区间法，构造了矩形置信区域，于1997年提出了一类基于该置信区域的新型最优准则——R-最优准则.关于R-最优准则的研究相对于其它最优准则，如A-最优准则、D-最优准则、E-最优准则和I-最优准则来说相对较少，仅赵洪雅等[3-4]介绍了二阶Scheffé正则多项式模型参数估计的R-最优，二阶可加混料模型参数估计的R-最优设计问题.李俊鹏等[5]讨论了q分量二阶混料K模型的R-最优设计.胡小玲[6]研究了二阶塌落模型的R-最优.而关于单纯形-中心多项式的研究，关颖男等[7]讨论了q-1阶多重线性多项式模型参数估计的A-最优设计，给出了一种A最优设计的算法，佟毅等[8]讨论了最优的单纯形-中心设计.基于此，本文将R-最优准则与单纯形-中心多项式结合起来，主要介绍q分量三阶中心多项式混料模型的R-最优设计，并给出设计柱点以及相应的测度.

1 q分量三阶中心多项式模型

对于q分量混料系统来说，q-1维正规单纯形Sq-1上的q阶单纯形中心多项式模型为

(4)

对于模型(4)，试验点安排在单纯形Sq-1上所有各类中心上的设计就是单纯形-中心设计，单纯形-中心设计是Scheffé在1963年提出的，在q分量单纯形-中心设计中，共有2q-1个不同的试验点，分别为q个纯混料、Cq2个二分量等比例混料和Cq3个三分量等比例混料，…，全部分量的等比例混料.

特别地，当m=3时，正规单纯形Sq-1上的q分量三阶中心多项式模型为

(5)

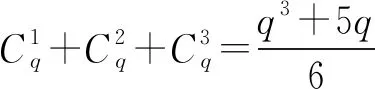
2 q分量三阶中心多项式模型R-最优设计

本文考察的是在混料系统正规单纯形Sq-1上模型(5)的R-最优设计，通过计算给出了该模型在Sq-1内的R-最优设计柱点及其测度.

引理1[9]对于混料区域Sq-1上的三阶中心多项式模型(5)，参数估计的最优设计柱点只能是Sq-1上的各类中心点.

设r1,r2,r3分别表示Sq-1上的每个顶点、两顶点中心及三顶点中心的测度，满足

则模型(5)所对应的设计矩阵X为

记测度矩阵为

则该模型所对应的信息矩阵M(ξ)为

M(ξ)=XTΛX=

利用文献[10]求3×3分块矩阵的逆矩阵的方法，求得信息矩阵M(ξ)的逆为

其中

由R-最优准则(3)可得如下约束极小值问题

利用拉格朗日乘子法，令

H(r1,r2,r3,λ)=

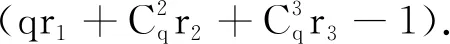
对r1,r2,r3,λ求偏导，得

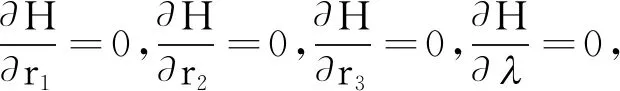
(6)

由于式(6)较复杂，不易求出r1、r2、r3的表达式，但当q为具体数值时，通过将q的值带入式(6)并结合软件mathematica可得到具体分量的三阶中心多项式模型的R-最优配置的数值解.

3 实 例

下面考察当q=3时模型(5)的R-最优设计.可直接将q=3带入式(6)，通过软件mathematica计算得到三分量三阶中心多项式模型的R-最优配置.也可通过该模型的信息矩阵，利用拉格朗日乘子法得到其R-最优配置.

设r1,r2,r3分别表示混料系统正规单纯形S3-1上的每个顶点、两顶点中心及三顶点中心的测度，满足

则该模型所对应的设计矩阵X为

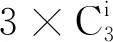
记测度矩阵为

则该模型所对应的信息矩阵M(ξ)为

M(ξ)=

其中，J3为元素均为1的三阶方阵.

易求得信息矩阵M(ξ)的逆为

其中

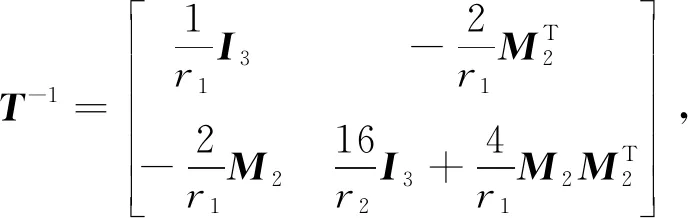
由R-最优准则(3)可得如下约束极小值问题

利用拉格朗日乘子法解该条件极小值问题，结合软件mathematica可得到如下结果：

r1→0.179 635 000 502 688 07,

r2→0.121 685 461 418 078 89,

r3→0.096 038 614 237 699 16.

因此，三分量三阶中心多项式模型的R-最优配置为

4 结 论

由于实际中需保持预测值的精度，需要适当提高模型的阶数，因此，对三阶中心多项式混料模型及其R-最优设计的研究是有必要的.本文从R-最优设计的理论出发，讨论了q分量三阶中心多项式模型的R-最优设计，并结合软件mathematica，得到了具体分量的三阶中心多项式模型的R-最优配置的数值解.为了求得模型的R-最优设计，需要得到模型的信息矩阵，通过最小化信息矩阵的逆矩阵的主对角线元素的乘积，利用拉格朗日乘子法解条件极小值问题，得到模型的R-最优设计.在这个过程中，由于R-最优设计的信息矩阵计算的复杂性，对于q分量的该中心多项式模型，不易求得其R-最优配置的数值表达式，但当q为具体数值时，通过软件mathematica较易得到具体分量的三阶中心多项式模型的R-最优配置.因此，随着计算机的不断发展，利用算法及相应的软件，使得对于模型的R-最优设计问题变得相对容易，从而可以按照需求解决更为复杂的R-最优设计问题.