量子强化学习技术及研究进展

韦云凯, 王志宏, 冷甦鹏

(1.电子科技大学 长三角研究院(衢州)，浙江 衢州 324000; 2.电子科技大学 信息与通信工程学院, 四川 成都 611731)

机器学习是实现人工智能的重要方法，其基本思想是理解和抽象人类智能行为，并在机器上实现同样的智能行为.从学习方式的角度划分，机器学习可以分为两大类.第一类是从数据中学习，包括监督学习(数据分类)和无监督学习(数据聚类)，这两种学习方式在大数据分析和数据挖掘中获得了广泛的应用；第二类是从交互中学习，即强化学习.强化学习是一种可以在陌生的环境中进行交互式学习的方法，其智能体能在完全未知的环境中学习和成长，从而可以适应各种未知的、复杂的，甚至是不断变化的应用场景，具有巨大的发展潜力与广泛的应用前景.

近年来，学术界和工业界对强化学习研究的兴趣与关注度持续上升.特别是AlphaGo[1]及其升级版本Alpha Zero[2-3]在围棋对弈中展现了针对人类围棋选手的明显优势之后，强化学习的研究与应用开始了爆发式的增长.然而，强化学习仍然存在众多典型的问题，例如探索和利用之间的平衡问题、面对复杂任务环境时的维度灾难问题等等，严重制约了强化学习的应用范围与效果.

日益发展的量子计算技术为解决强化学习所面临的问题带来了曙光.传统电子计算机只能一次处理一个比特的数据，并不能在真正意义上实现数据的并行处理.而量子计算机的量子比特存在叠加态，即量子态|0和|1的叠加态，一个量子比特一次运算能同时处理两个比特数据，对于n个量子比特即可并行处理2n个比特的数据.因此，量子计算机在储存能力和数据处理能力方面都远超经典计算机，从而可望解决强化学习中的平衡和维度灾难等问题.

量子计算始于Manin[4]和Feynman[5]分别于1980年及1982年的研究，这些研究指出，在某些量子系统演化的计算问题上，传统计算机是无法比拟的.1999年Shor[6]提出因子分解算法，实现了因子分解的指数级加速.1996年，Grover[7]提出量子搜索算法，实现了对无结构搜索问题的二次式加速.2016年，Crosson等[8]提出了量子模拟退火算法，对量子计算机的设计产生了显著影响.当前，越来越多的大型信息技术公司和研究机构都对量子计算展开了深入的研究.谷歌公司于2018年展示了其72量子比特计算机Bristlecone，并于2019年10月发表论文，展示了一个53位量子比特的计算机超算能力[9].IBM公司也于2019年9月公布了其对53位量子计算机的研究成果.

量子计算的发展使其与强化学习的融合成为了可能，研究人员将量子计算与强化学习相结合，提出了量子强化学习技术.在该技术研究中，一方面研究人员基于量子力学特性，改进强化学习算法本身，可开发更加智能高效的量子强化学习算法；另一方面，将经典环境量子化，进而将智能体同环境间的交互量子化，设计更加高效的量子强化学习框架.虽然总体而言，量子强化学习当前主要停留在理论研究和实验探索的起步阶段，但是，随着量子计算机研究的不断进步，量子计算以及量子强化学习理论的不断深入，会有许多结合量子计算和强化学习理论的新算法被提出，这将极大地促进量子强化学习的迅速发展，推动人工智能技术的根本性进步.

1 量子计算与强化学习

1.1 量子计算

量子计算是一种遵循量子力学规律，调控量子信息单元，进行计算的新型计算模式.传统计算机的模型是通用图灵机，与之相对应，通用量子计算机其理论模型是用量子力学规律重新诠释的通用图灵机.量子力学态叠加原理使得量子信息单元的状态可以处于多种可能的叠加态，从而导致量子信息处理在效率上相比于经典信息处理具有更大潜力.普通计算机中的2位寄存器在某一时间仅能存储4个二进制数(00、01、10、11)中的一个，而量子计算机中的2位量子位(Qubit)寄存器可同时存储这四种状态的叠加状态.随着量子比特数目的增加，对于n个量子比特而言，量子信息可以处于2n种可能状态的叠加，配合量子力学演化的并行性，可以展现比传统计算机更快的处理速度.

本小节后续内容将首先介绍量子计算中的一个基本概念，即量子叠加态；接着，介绍在量子计算中执行计算任务的基本单元——量子门；对于获取量子计算结果的方法，介绍基于量子坍缩假设的测量；最后，介绍在量子计算中量子并行性计算的基本概念.

1.1.1 量子叠加态

和经典比特类似，量子计算的基础是量子比特.量子比特的两种状态可用狄拉克符号|·分别表示为|0和|1，对应于经典计算的比特0和比特1.但是，不同于经典计算的是，一个qubit可以处于叠加态

|ψ=α|0+β|1

(1)

其中，α和β是复数，且满足|α|2+|β|2=1.对于一个n位qubit而言，由一个n维希尔伯特空间的复向量表示：

(2)

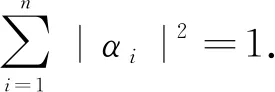
1.1.2 量子门

在经典计算中，逻辑操作是通过逻辑门来完成的，如非门、与门和异或门等.在量子计算中，计算任务通过量子门实现，当前量子非门和量子控制非门已经在量子计算中实现.所有的n量子门都对应一个可逆的n×n酉变换U，且满足

UU†=U†U=I

(3)

其中，符号“†”在量子计算中表示共轭转置.

(4)

1.1.3 测量

对量子系统而言，其状态处于叠加态，为了观测该系统，需要对系统进行一次测量.测量过程基于量子坍缩假设，即处于叠加态的量子系统，在测量时以对应的概率不可逆地坍缩到一个基态.定义一组测量算子{Mm}，满足完备性

(5)

其中，m对应于可能得到的测量结果，如果用算子Mm对叠加态|ψ进行测量，最终得到m的概率为

(6)

测量后得到的状态为

(7)

1.1.4 量子并行性

在量子计算过程中，最基础的操作是作用于量子比特的酉变换，将U作用于处于叠加态的量子比特上，该变换将作用于该叠加态的所有基态上，并输出一个新的叠加态.这个过程很像输入一个x(即叠加态的一个基态)，给出结果f(x)，因此被称为量子并行性.该特性是量子计算中最重要的，但是由于量子坍缩假设，每次测量只能观测到一个运算结果，这种并行性不能直接运用.该过程可用以下公式描述：

(8)

1.2 强化学习

本小节首先介绍了强化学习的基本原理.由于标准的强化学习框架是基于马尔可夫决策过程的，进而介绍了马尔可夫决策问题，并阐述了基于值函数迭代的马尔可夫决策问题求解方法，以及该方法中存在的问题.最后，介绍了利用Q函数解决马尔可夫决策问题的初步方法.

1.2.1 强化学习基本原理

强化学习主要用于解决智能体(Agent)同任务环境交互来学习最优动作策略，以最大化累积奖励值的问题.其基本原理如图1所示，在智能体同环境交互过程中，如果智能体的某个动作导致环境反馈正的奖励值，则智能体接下来产生该动作的策略会加强；反之，产生该动作的策略将减弱，以此来不断获得更高的累积奖励值，从而经过迭代获得最佳策略.

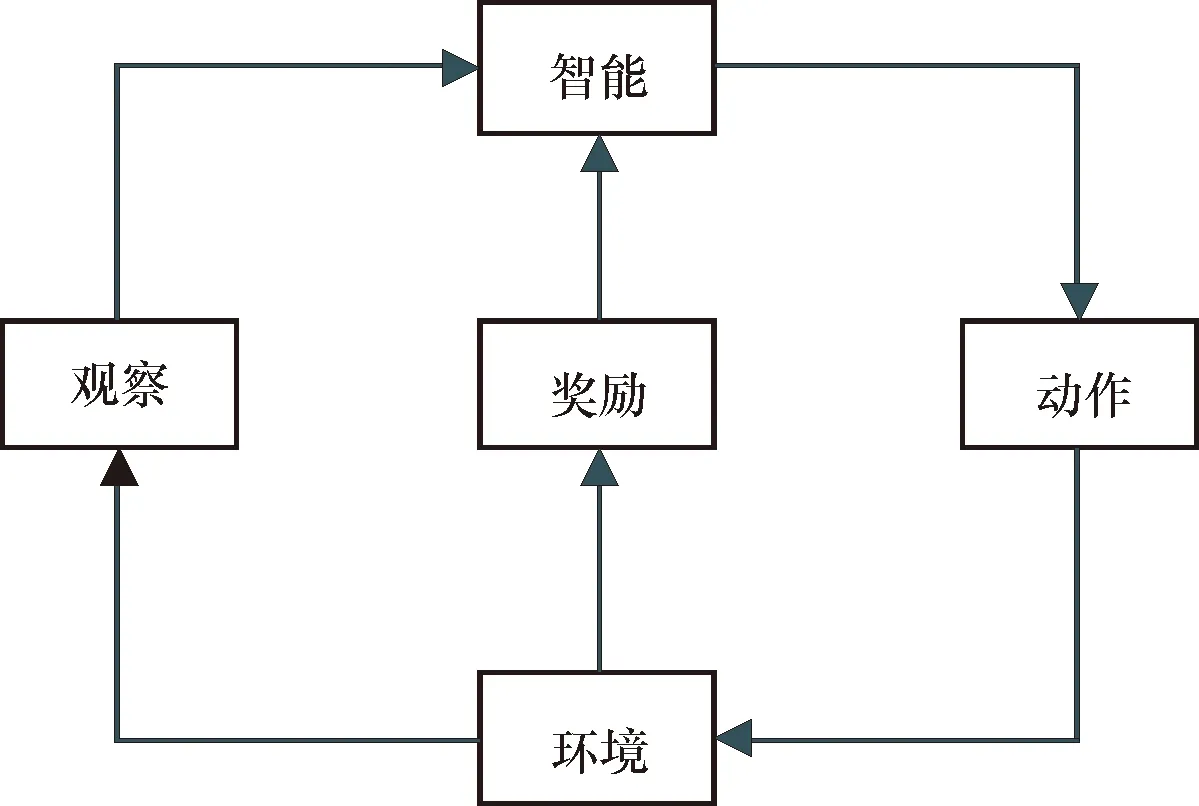
图1 强化学习基本原理

强化学习的基本要素有策略(Policy)、奖励(Reward)、值函数(Value function)和任务环境(Environment).由图1可知，首先智能体感知当前状态Si，在动作空间A中选择动作ai执行；接着智能体转移到新的状态Si+1，并获得相应的奖励值ri+1，智能体依据奖励值来调整自身策略并针对新的状态做出新的决策.强化学习的目标是找到一个最优策略π*，使得智能体能在任意状态和任意时间步骤下，都能获得最大的累积奖励值：

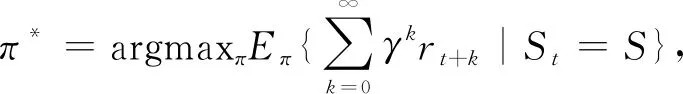
(9)

其中，π表示智能体的某个策略，γ∈[0,1]为折扣因子，k为未来时间步骤，S为某个状态空间.

1.2.2 马尔可夫链决策过程

标准的强化学习方法是基于离散时间、有限状态的马尔可夫决策过程.该马尔可夫过程包括如下4部分.

(1)有限的状态集合S和动作集合A，其中，状态表示环境可能处于的状态，动作表示智能体可执行的动作；

(2)由状态转移矩阵P(s′∈S|s∈S,a∈A)定义的受控马尔可夫链；

(3)实函数r:S×A→R，即奖励函数；

(4)常数γ∈[0,1)，即折扣因子(Discount factor).

静态策略函数π:S→A，该函数表示在受控马尔可夫链处于状态s时，可根据π(s)选择下一步动作，进而状态转移矩阵可表示为P(s′|s,π(s)).马尔可夫决策问题的目标为获得最优策略：

π*=argmaxπV(π,s)

(10)

其中，

(11)

1.2.3 值函数迭代

值函数可以以迭代的方式表示为

(12)

进而获得贝尔曼方程：

(13)

该方程即为强化学习过程中的目标.使用贝尔曼方程(13)进行值函数计算的方法，称为值函数迭代.但是，随着状态空间S和动作空间A的维度增大，强化学习就会出现维度灾难问题.同时，值函数迭代方法需要状态转移矩阵和奖励函数的全部信息，否则是无法获得最优值V*的.

1.2.4 Q函数

Q函数即“动作-值”(Action-value)函数，定义：在马尔可夫链中(对于静态的策略π)，从(s,a)到期望的奖励值的映射，且s和a分别为初始的状态和动作.

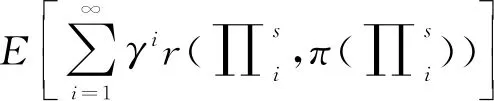
(14)

从而，易得

V(π*,s)=maxaQ(ππ,s,a)

(15)

同时，因为Q*(s,a)=maxπQ(π,s,a)=Q(π*,s,a)，可将马尔可夫链的最优策略表示为

π*(s)=argmaxaQ*(s,a)

(16)

即通过计算Q*(s,a)就可以解决马尔可夫链决策问题.对于Q*(s,a)的贝尔曼方程可表示为

Q*(s,a)=E[r(s,a)]+

(17)

即依靠式(17)对Q*(s,a)进行数值估计，即可得到最优策略.

2 量子强化学习

量子计算与强化学习的融合催生了量子强化学习技术.当前，量子强化学习技术的研究主要分为两大类：第一类是利用量子特性对传统强化学习算法机制和学习效率进行改进，第二类是设计量子式的智能体同量子化环境的交互方式，进而给出新的量子强化学习框架.本节将重点介绍量子强化学习的研究进展与基本机制.

2.1 量子强化学习研究现状

如前所述，量子强化学习技术的研究分为两大类.针对第一类利用量子算法提高强化学习效率的研究，2008年Dong等[10]发现，结合量子算法特性可对传统强化学习算法表现进行改进，并由此提出了结合量子坍缩和Grover算法的新强化学习算法.2012年，Briegel等[11]提出投影模拟(Projective simulation)强化学习模型，并给出了其量子版本；2014年，Paparo等[12]给出了基于rPS投影模拟模型，利用其量子漫步实现二次加速的方案；2015年，Dunjko等[13]给出了rPS投影模拟模型的灵活模块化设计架构及其量子化方法.Crawford等[14]于2019年提出了基于量子玻尔兹曼机的强化学习方法，来实现对强化学习算法的加速.

第二类研究主要是给出了量子化的交互方式以及经典环境量子化理论，设计新的量子强化学习框架，以对强化学习效率进行改进.该方向主要研究智能体在量子环境中进行交互式学习的模式、经典环境量子化方法，以及基于量子式交互框架对学习效率的二次式和指数级加速.Dunjko等[15]给出了智能体在量子化环境进行交互的理论框架，及其对学习效率二次式加速[16]和元学习方法进行二次式加速[17]的强化学习方法，同时，在后续研究中给出了对量子强化学习方法的学习效率进行指数级加速的理论研究结果[18]，并进一步给出变长周期性环境的量子化方法[19].受限于量子计算机的发展，这类研究仅仅提出理论上的量子强化学习框架，还没有在真正的量子计算环境下进行实验验证.

2.2 量子强化学习基本机制

量子强化学习基本机制如图2所示，量子强化学习同样是基于交互的学习过程，其交互过程可以分为经典交互方式和量子化交互方式.经典交互方式主要包括经典任务环境同量子化智能体的交互，以及经典智能体和量子化任务环境的交互过程，目前的研究只涉及前者.量子化交互方式即量子化智能体同量子化任务环境的交互过程.

图2 量子强化学习基本机制

量子强化学习中对于交互过程，采用了动作空间和感知空间进行描述.同传统强化学习相比，量子强化学习采用特征状态(Eigen states)和特征动作(Eigen actions)分别进行描述，但是量子强化学习的任意状态和动作可处于多种特征动作和特征状态构成的相应叠加态下.下面分别对量子强化学习中感知空间和动作空间，以及特征状态和特征动作进行介绍.

2.2.1 感知空间和动作空间

在量子强化学习中，智能体和环境的交互主要为环境反馈感知(Percepts)和智能体可执行的动作，其中，感知包括环境奖励和环境的其他信息.感知s被表示为希尔伯特空间的正交状态基|s，感知空间即希尔伯特空间：

S=span{|s|s∈S}

(18)

其中，S表示感知集合.同样，动作空间可以表示为

A=span{|a|a∈A}

(19)

其中，A表示动作集合.同时，有a|a′=δa,a′，δ表示克罗内克函数.从而历史状态(Histories)的希尔伯特空间可以表示为A⊗S⊗A….

2.2.2 特征状态和特征动作

在量子强化学习方法中，传统的状态和动作定义分别为特征状态|s和特征动作|a.而根据量子叠加原理，任意的状态可以表示为

(20)

同时，任意状态可表示为

(21)

其中，

(22)

而这种任意的状态和动作在经典算法中没有明确的意义，但是对于量子系统是确实存在的.|αn|2(或|βn|2)表示对应特征状态|sn(特征动作|an)的概率.Ns和Na分别表示特征状态和特征动作的数量，所需表示该量子强化学习系统的量子比特数目满足：Ns≤2m≤2Ns,Na≤2n≤2Na，即使用m和n位量子比特分别来表示特征状态集合S={|si}和特征动作集合A={|aj}.因此，存在以下关系：

(23)

(24)

即在量子强化学习系统中，动作(状态)可以处于特征动作(特征状态)的叠加态，概率幅Cs和Ca是复数，且满足

(25)

3 经典环境基于量子特性的强化学习

量子化智能体同经典任务环境的交互过程中，主要依靠量子计算特性对量子化智能体的计算复杂度进行改进，以加快其学习过程.这方面的研究主要包括基于量子算法对强化学习动作策略更新方式的改进[10]，采用量子随机漫步算法对投影仿真模型的量子化[11-13]和基于量子玻尔兹曼机方法对Q-Learning方法的改进[14].下面将分别进行介绍，并对量子强化学习的仿真结果进行对比分析.

3.1 基于量子算法对强化学习动作策略的改进

在强化学习算法中，探索与利用之间的平衡问题一直是动作选择策略中的核心问题.当前广泛应用的动作选择策略ε-greedy[20]和Softmax[21]，在一定程度上解决了探索和利用之间的平衡问题，但其面对变化的复杂任务环境仍有很大局限性.

Dong等[10]于2008年提出的量子强化学习算法，主要是对动作选择更新策略做出了改进，使用该方法可以加速动作选择策略更新过程，且更好地平衡探索和利用.该算法对动作选择策略更新的加速以及优化，得益于量子坍缩的特性和量子并行性，这是由量子力学的性质所决定的.量子计算中，使用希尔伯特空间中的向量来描述物理系统，希尔伯特空间本身具有完备性，且其向量满足叠加性原理，则对希尔伯特空间中的向量进行操作，即对于多个态实行并行性操作.对于一个处于叠加态的量子系统，对其进行一次测量，该系统就会不可逆地以相应的概率坍缩到一个确定的状态上.该量子强化学习算法中，动作选择使用量子坍缩原理，动作选择策略可表示为π:S→A，即有

(26)

根据量子坍缩原理，对动作空间进行一次观测，即可以概率|Ca|2得到相应的特征动作|an.

动作选择策略更新的核心是Grover iteration,即和Grover Search算法[7]使用相同的核心算法.首先，用nHadamard门准备等权重特征动作的叠加态：

(27)

其次，酉变换可表示为

(28)

其中，

Ua=I-2|aa|

以该酉变换对相应的动作执行操作，可增大该动作在策略选择中的概率幅.对于每次交互选定的动作|a，执行L次策略更新，其中

(29)

更新后可得到

cos[(2L+1)θ]|a⊥

(30)

即通过Grover iteration，动作|a对应的概率从1/2n升高为sin2[(2L+1)θ]，该算法流程如算法1所示.

算法1 量子强化学习算法

REPEAT (for each episode)

FOR all |sin |s(m)DO

1. 观测|a(n)，得到动作|a

2. 执行|a，得到状态|s′和奖励r

a) 更新状态值V(s)

b) 更新概率幅

执行L次幅值放大

END FOR

UNTIL |ΔV(s)|≤ε

该量子强化学习算法主要依靠Grover算法的核心思想——量子幅值放大，并结合量子坍缩原理来构造量子强化学习的动作策略.相比于传统强化学习算法，在该量子强化学习算法中不是智能体主动地进行动作选择，而是利用量子坍缩假设，进而本质上以一种概率的形式实现了探索与利用之间的平衡，并利用Grover iteration对策略更新进行了加速优化.但是，该算法在Q函数值更新方面并未结合量子计算特性，依然采用传统更新方法，对于大规模的状态空间收敛效果会变差.但是这种基于量子叠加态和量子坍缩原理的动作策略，对于解决强化学习探索和平衡问题给出了很好的借鉴意义.

3.2 投影仿真模型量子化

最早的量子强化学习方法之一是Briegel等[11]于2012年基于物理学角度提出的投影模拟(Projective Simulation，PS)方法.PS模型给出了灵活的主动学习智能体框架，并且提供了自然的量子化方法.以下主要对投影仿真模型及其量子化方法进行概述.

3.2.1 投影仿真模型

PS基础模型假设时间和感知空间都是离散的，其核心概念为智能体的记忆——经验组合记忆(Episodic and Compositional Memory, ECM).ECM为经验组成的网络，每个网络节点称为clips或者episodes.每个clip标记为ci，且ci∈S∪，S表示感知空间，表示动作空间.ECM的一种可能结构如图3所示，该结构以环境反馈的感知s为开始，执行多次随机漫步(Random walks)，每次随机漫步都会给出一个可能的动作ai，该动作不在真实的环境中执行.只有在给定的思考时间(Reflecting time)之内，评估局部最优的动作a才会在真实环境中执行，进而以执行结果(环境反馈)更新网络结构.

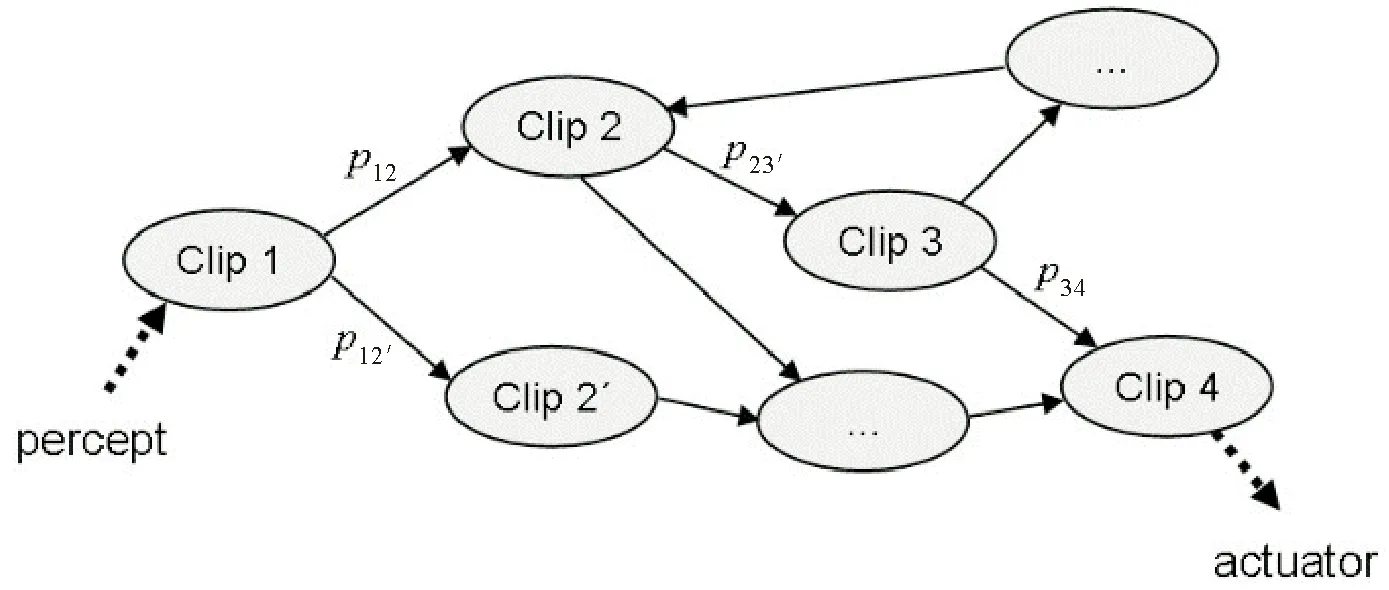
图3 经验组合记忆网络结构

Briegel等[11]同时提出了基于在PS网络上进行量子漫步(Quantum walks)的量子化改进方法.该方法主要利用Liouvillean dynamics(量子密度算子的主要方程)来代表PS模型的思考(即在ECM网络上进行随机漫步)过程.该量子化方法在思考时间和智能体内部可实现的策略空间上提出了可能的提升.

3.2.2 投影仿真模型量子化

另一种对PS模型进行量子化改进的方式由Paparo等于2014年提出[12].作者主要在离散时间进行量子漫步的框架下，基于rPS智能体模型给出了对思考时间的二次式加速.该方法的核心思想为：对于一个给定的状态转移矩阵P，给出一个量子漫步对应的酉变换算子UP，且该算子的光谱特性和状态转移矩阵P本身相关.

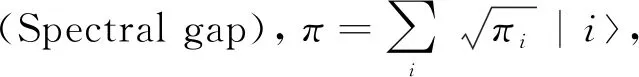
UP|π=|π

(31)

3.3 基于玻尔兹曼机的强化学习方法

Crawford等[14]于2019年基于深度玻尔兹曼机(Deep Boltzmann machine)，并结合量子模拟退火算法训练量子强化学习，来实现可能的强化学习加速.该方法的核心是利用玻尔兹曼机的负自由能(Negative free energy)来近似Q-learning的Q-function：

Q(s,a)≈-F(s,a)=-F(s,a;θ),∀(s,a)∈S×A

(32)

同时，利用量子玻尔兹曼机的平衡自由能对F(si,ai)近似.该量子强化学习算法，主要对计算复杂度较高的Q函数计算更新以及策略更新进行改进，相对于传统的Q-learning算法而言，其加速效果主要源于该部分.由于技术限制，该方法并未提出切实可行的物理实验方案，但是仍然给后续研究提供了非常好的借鉴意义.

3.4 对量子强化学习算法的仿真分析

迷宫问题是强化学习方法开发和测试的典型问题，在基于量子算法对强化学习动作策略改进[10]和基于量子玻尔兹曼机的强化学习方法[14]中都分别给出了采用量子强化学习算法解决迷宫问题的仿真结果，如表1所示.从结果分析可知：①采用经典计算机模拟的量子强化学习算法性能，已经在一定程度上优于传统强化学习算法，即可从量子算法中获得启发对传统强化学习算法进行改进；②量子算法对强化学习动作策略改进中，量子特性为强化学习中探索和利用的平衡问题给出了良好的解决方案，但是对迷宫状态规模对算法性能的影响并没有给出详细研究对比；③量子玻尔兹曼机为强化学习算法提供了可能的加速，且在规模增大时算法收敛性良好，但是对于迷宫规模增大时的对比实验，只给出了基于受限玻尔兹曼机的强化学习和基于深度玻尔兹曼机强化学习的对比结果，对基于量子玻尔兹曼机的强化学习并未给出详细的实验对比结果.

表1 量子强化学习仿真实验对比分析

4 量子环境下的强化学习

量子环境下的强化学习，即将任务环境量子化，让智能体在量子化的环境中学习，利用量子式交互提高其学习效率.Dunjko等[15]最早在2015年，提出了智能体在量子化的环境中学习的框架，并且详细讨论了该框架在经典环境中如何应用.其后的研究主要是三个方面：①讨论了经典环境量子化的可行性，并且给出了对学习效率进行二次式加速的可行性[16]；②进一步讨论了经典强化学习环境较为一般的量子化方法，以及基于此进行学习效率提升的可行性；③主要讨论了在量子环境中，通过将智能体和环境的交互量子化，来进行量子版本的元强化学习[17]；最后，将马尔可夫决策过程和Simon’s Problem相结合，给出了对量子环境中智能体学习效率进行指数级加速的可行性[18].

4.1 智能体同量子环境交互框架

Dunjko等[15]在2015年提出智能体在量子环境下的交互框架，并讨论了任务环境量子化方法，进而研究了对强化学习效率进行二次式加速的可能性.该框架的核心是构建和经典环境交互等价的量子式交互.量子化的智能体和量子化的任务环境系统各自对应一个希尔伯特空间，即动作空间A和感知空间S.智能体和环境作用于一个公共的通信寄存器RC上，该通信寄存器可表示任意的动作和感知序列.进而，智能体(或环境)可以描述一个轮流作用在通信寄存器RC上的映射序列({A}{E})，且拥有私有的寄存器RA(RE)构成其内部存储，如图4所示.

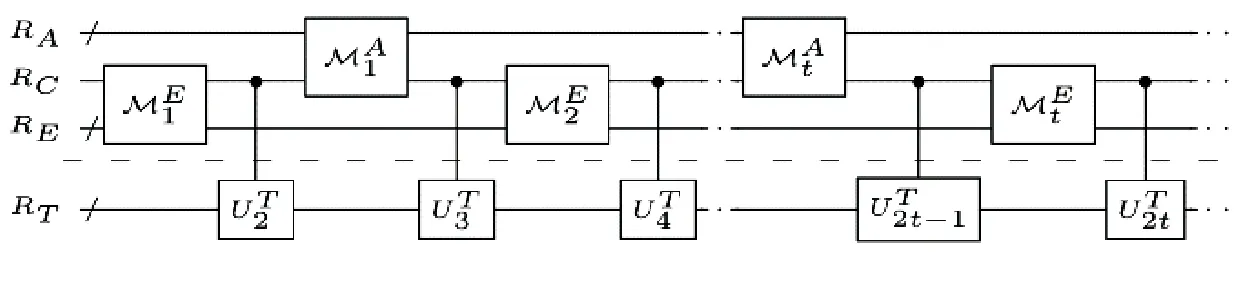
图4 量子化交互框架

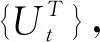
(33)

基于此量子化的交互框架，Dunjko等[16]进一步给出了结合Grover Search算法的任务环境量子化方法，并结合该方法提出了对学习效率进行二次式加速的可能性.对于一个严格周期性、单一奖励的环境(即该环境只在任务完成时给出一个奖励)，该环境可以量子化为一个相翻转数据库(Phase-flip oracle)：

(34)

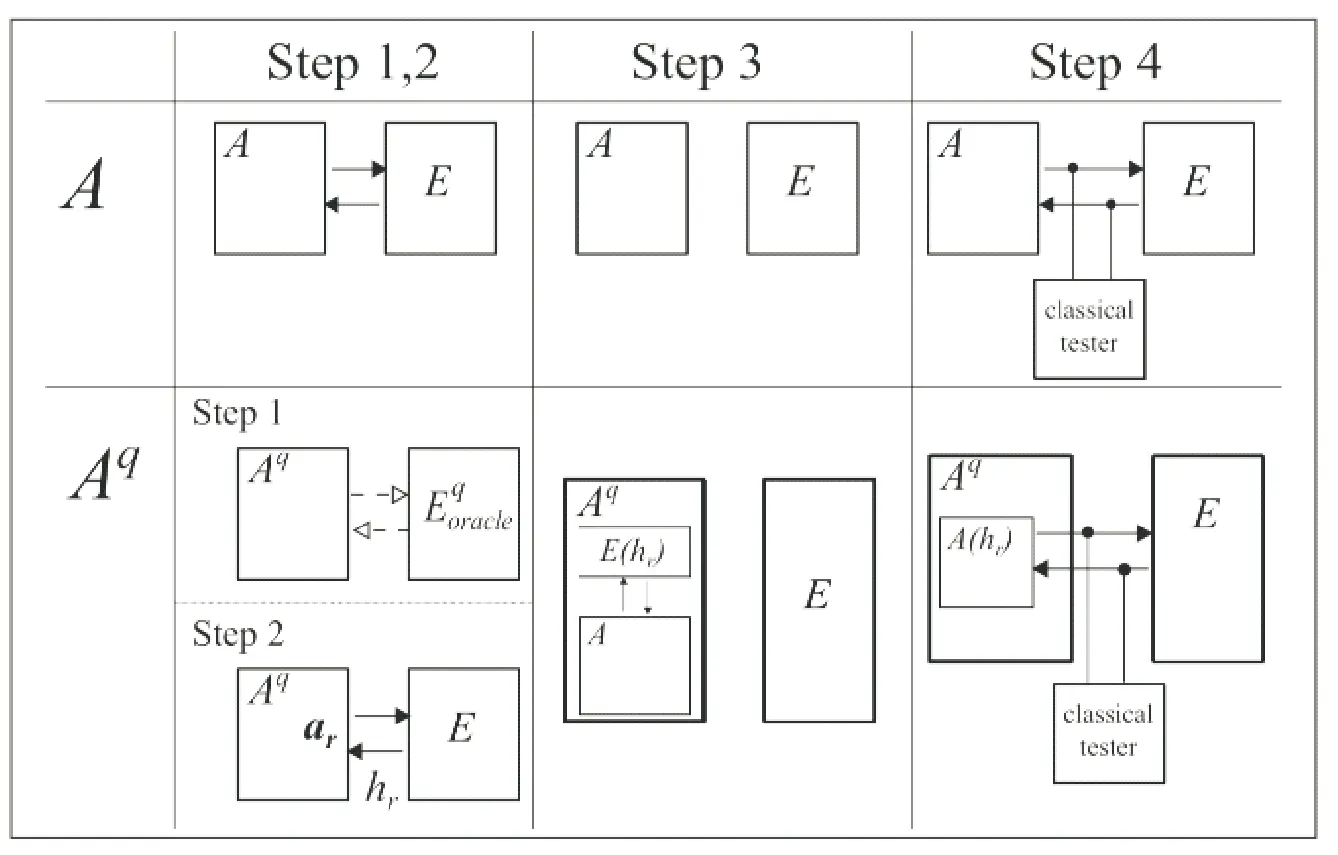
图5 量子化智能体和传统智能体训练对比

该框架给出了量子化智能体同量子化环境交互的可行方案，同时从理论上讨论了对基于模型的强化学习过程进行二次式加速.但是讨论的任务环境很简单，仅仅在一些简单的棋类游戏上适用，对于更复杂的不确定性环境没有给出可行的量子化方案.并且该框架仅限于理论，没有提出可行的物理实验方案.

4.2 经典环境量子化方法

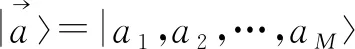
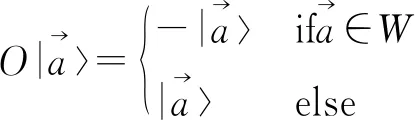
(35)

进而结合量子搜索算法Grover Search分析了结合该环境实现量子强化学习效率二次式提高的可行性.

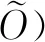
将经典环境进行量子化，对于进行量子化的交互是很重要的环节.一般性的任务环境量子化方案研究将成为量子强化学习技术中很重要的一个研究方向.

4.3 量子元学习

对于交互式学习而言，其学习效率不仅仅取决于与环境的交互效率，智能体本身的参数也会对学习效率产生很大影响，如ε-greedy中平衡探索和利用的参数ε，对于不同的环境，其值也应该有相应的调整.在实际应用中，这些参数是用户手动调整的.而该过程是可以自动化的，即智能体可以根据环境的变化动态调整自己的参数，称为元强化学习.Dunjko等[17]于2017年给出了元强化学习的量子版本，即量子元学习.量子元学习的核心在于将智能体同任务环境的交互过程视为一个系统，进而利用量子离散优化技术[23]找到该系统的最优状态，实现量子元学习的过程.结合元学习，对于确定性任务环境而言，其量子化交互系统的状态可以表示为

|p.M.A.=

|km.m.p|eval(k)|memAm.m.p|aC|stateE

(36)

其中，|km.m.p表示学习模型的原参数，|memAm.m.p表示智能体的储存，|aC表示当前的智能体动作，|stateE表示环境的纯态，eval(k)用来衡量当前环境下参数k的表现.利用量子离散优化问题，让元参数|km.m.p初始化为等幅值的叠加态，有

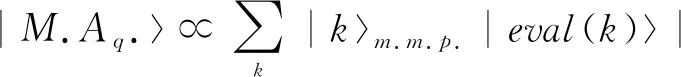
(37)

下面进行类似于Grover算法的过程，对该学习过程进行二次式加速.该过程将给出最优的eval(k)值，即可以找到在当前环境下最优的模型参数k的具体值，进而利用该参数下智能体同环境的交互历史对智能体进行预训练过程，从而提高智能体的学习效率.

该方法在理论上给出了量子版本的元强化学习可行性，同经典环境下利用梯度下降进行元学习对比而言，获得了很好的加速效果.但仅仅是对于确定性环境给出了详细的论证，不确定性环境的量子化还需进一步讨论，且该方法并无可行的物理方案提出.

4.4 基于量子环境的学习效率指数级加速

在智能体同量子交互的强化学习框架内，Dunjko等[18]于2018年提出了量子化智能体可对学习效率实现指数级提高的量子强化学习方法，远远超过了之前的二次式加速结果.该量子强化学习方法，主要借助于将任务环境量子化为更特殊的无结构数据库搜索问题——Simon’s Problem[24]，以实现对量子化智能体学习效率的指数级提高.

在该量子强化学习方法中，通过将马尔可夫过程和Simon’s Problem结合，对马尔可夫过程量子化.该马尔可夫量子化过程可表示为

fs:X→Y

(38)

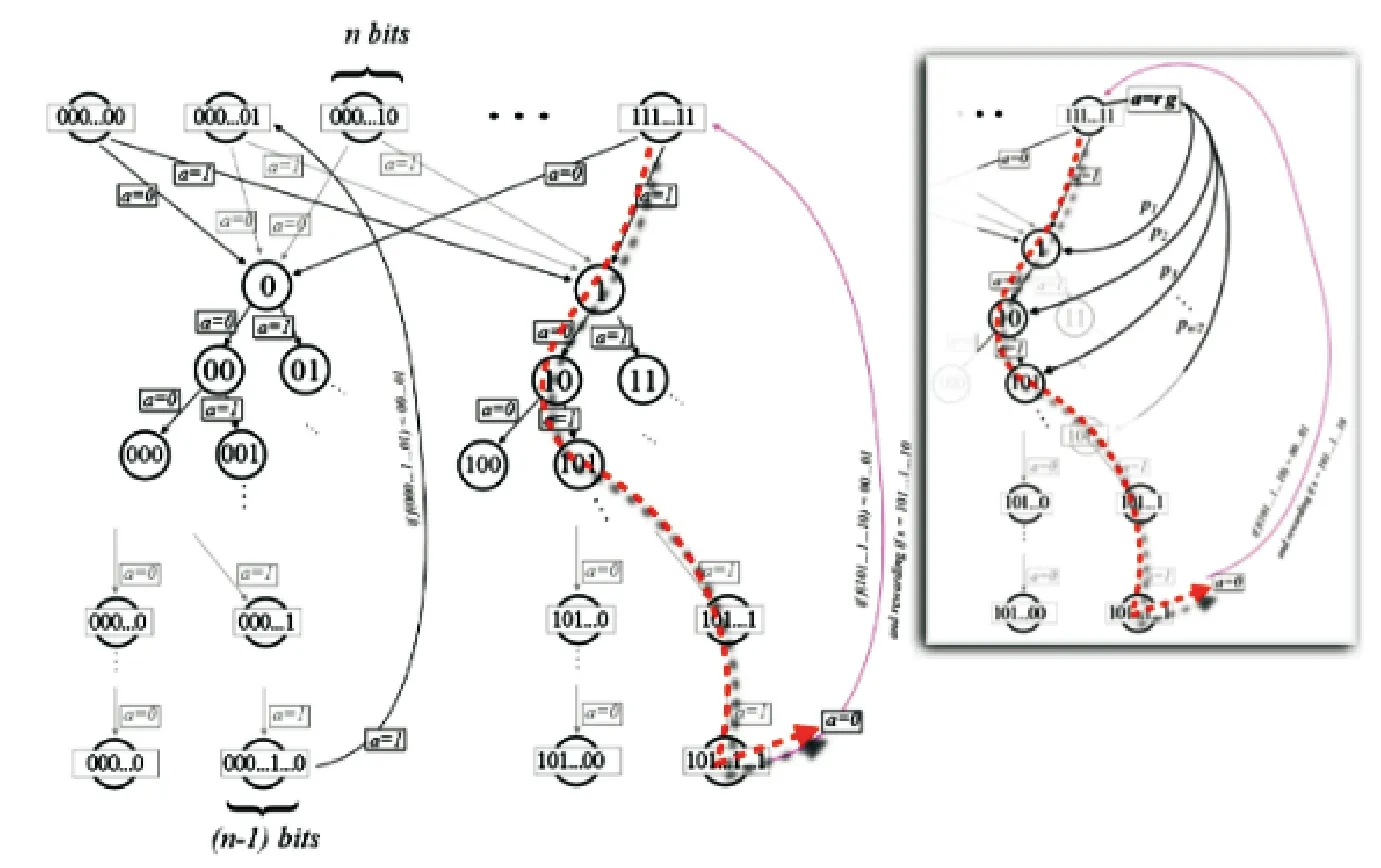
图6 结合Simon’s Problem的马尔可夫决策过程

方框外的部分表示随机跳跃动作rg的马尔可夫决策过程，即确定性环境，智能体在每一步有两个动作，即{0,1}.动作序列形成了一个深度为n-1的树，最后一次动作会引起零层状态的转移，即进行一次查询动作，进而得到相应的结果.每一条这样的路径构成一个猜测guessx，如果为s，则该路径会得到一个奖励(路径在图中以红色虚线和粉色的线标出).如图6所示，方框内画出了加入随机跳跃rg的情况，即在受奖励的路径中，从零层状态随机跳跃到该路径的任意状态继续进行训练的过程.

对结合Simon’s Problem进行量子化马尔可夫决策过程的利用，智能体可实现进行一次查询的交互步骤为O(m)，按照西蒙算法，可在O(m2)的复杂度下以较高概率找到s，即找到一个受奖励路径，结合前文中量子化智能体同量子化环境进行交互的框架实现对智能体的预训练.而在经典计算方法下，解决一个交互周期为m的任务环境，Simon’s Problem需要的复杂度为O(2m)，对于复杂的环境而言，现有的经典计算资源是无法实现的，结合量子化可以指数级地提高量子强化学习的学习效率.

5 应用展望

以上部分对近年来量子强化学习方法研究进行了概述，这些研究显示了量子计算对强化学习多方面的优化，包括策略更新方法、值函数估计、学习效率优化等等.随着该领域研究的不断深入，将对包括物联网、智能控制、智慧城市、产业升级等众多领域产生重大影响，促进智能时代的到来.

5.1 物联网

一方面，物联网发展速度很快，但是在安全和隐私、计算资源分配、能源分配等方面的问题还需要更优的解决方案；另一方面，在智能交互的物联网设计中，传统的强化学习方法对大规模的数据处理和复杂环境的快速适应方面，还面临着环境不完全感知、学习效率极低、计算资源不足等问题.量子计算和量子强化学习的结合发展，将在这些方面产生重大影响，带来强大的传感器网络、高效的大规模数据处理能力以及极低延迟的实时智能交互.

5.1.1 强大的传感器网络和高效的数据处理能力

在未来物联网中，传感网络的感知能力能否全面、准确、无感地收集环境信息是十分重要的，这对传感器的微型化、低功耗、高性能等方面提出了新的挑战.在量子技术中，量子点技术的进展针对该问题给出了新的解决方案.量子点一个很重要的特性是，可以在很宽的波长范围内被激发，并且发射较短的光谱.2003年，Walker等[25]基于量子点的特性实现了量子点光学温度探头.2011年，Zora等[26]在研究中说明量子点非常适用于基于能量传递的新型化学传感器.该方法给出了可能的基于量子点传感器系统的通用设计方法.随着量子点的不断发展进步，传感网络将愈加强大.

物联网的异构性和高度的复杂性产生了大量不同种类的数据，包括位置信息和环境产生的数据、历史记录数据、传感器数据和命令数据等等.随着物联网设备数量的持续性增加，要存储和处理的数据也越来越多，成为物联网发展最重要的问题之一.在大规模物联网中，大量的物联网设备和传感器的搜索及感知以及多目标优化也成为很大的问题.一方面，量子计算将提供十分强大的计算能力，给有效地处理大规模数据提供了新的机遇；另一方面，量子搜索算法，比如Grover算法对搜索问题实现了二次式的加速，由此可对大规模物联网中传感器的搜索问题实现优化.结合量子强化学习，将对未来物联网的大规模数据分析能力产生如下影响.

(1)量子计算给量子化智能体提供了极高的运算能力，智能体可以在短时间内对环境数据完成分析.对于物联网不断变换的复杂环境，智能体可基于大量数据分别对感知层、网络层和应用层完成分析优化，一方面可建立一个或者多个基于模型的量子化智能体，以进行对环境的量子化模拟；另一方面，对于无模型的智能体，可快速完成策略更新，同时基于当前环境信息和历史经验，快速形成最优动作策略.

(2)基于模型的量子化智能体能够以极高的学习效率，在较少的交互步骤内对复杂的环境进行分析学习，包括对感知层、网络层和应用层环境快速感知学习，以便在很短的时间内适应不断实时变化的网络环境.

结合量子强化学习的大规模物联网，可对现实复杂环境实现全面观测，同时量子化智能体可对实时的大规模数据进行分析，快速执行动作策略的更新等操作，从而面对不断变化的物联网系统，实现快速的适应与预测.

5.1.2 极低延迟的实时智能交互

在智能交互的物联网中，获取系统状态和实时控制系统面临的随机时延问题，会对整个系统性能产生很大影响[27]，且目前还未提出有效的解决方式.该时延受多方面的影响，包括边缘服务器/雾服务器/云服务器及通信网络中的通信和计算资源状态等等.目前，已经有一些基于强化学习的研究来改进这些问题[28-29]，但是对于不断变化的复杂环境所要求的算力和学习效率依然不适用.同时已经有一些基于强化学习的研究给出了智能交互式物联网和智能城市的设计工作[30]，提出了该领域需要解决的问题，包括：对环境的不完全观测问题、延迟控制问题、多智能体的协作控制问题等等.对于环境的不完全观测问题，结合持续发展的量子点传感器网络，有望实现对环境的全面感知.同时，随着量子强化学习的深入研究，将在两个方面产生影响.

(1)量子化智能体能够以很高的学习效率，快速适应不断变化的网络环境，实现快速实时的网络资源优化，进行快速的智能主动缓存和智能化的移动边缘计算等等，从而降低交互过程中的通信时延.在Dunjko等的研究中，给出了对量子化交互的二次式甚至于指数式的加速.量子强化学习在该研究方向的持续性推进，并且结合量子通信技术的进步，将会对通信效率产生极大提升，进而对物联网的通信资源分配、控制延迟等方面给出彻底的解决方案.

(2)结合量子强化学习方法，量子化智能体有望实现极短时间内对交互信息作出优化的智能响应.量子化智能体在学习效率和大规模数据的分析能力方面，都远远超过传统智能体，在复杂的环境中可实现快速适应，从而为高度异构性网络结构的互操作性提供可能的解决方案.

5.2 智能控制

在智能控制领域，量子强化学习可能的应用主要包括两个方面：①量子强化学习在大规模工业控制系统自动化方面有望给出解决方案，为工业控制带来升级；②在量子实验自动化控制方面，采用完全量子化的强化学习方法进行量子实验控制，对量子计算机计算速度和精确性方面可能带来全面的提升.

5.2.1 大规模工业控制系统

对于复杂的控制体系而言，它是由多种模块构成的多重结构，在时间和空间尺度上都会呈现出大量不同特征.大规模的控制体系必然会引入大型传感网络和通信系统，大型传感网络能够提供丰富的系统信息，实时快速地充分利用丰富的数据生成最有价值的信息，而通过分析产生控制、管理与决策的命令成为了巨大挑战；同时，原有的控制系统中信息传递被假定为不受融合通道限制，而通信系统的引入会造成信道容量、传输时延等方面的限制，这给原有的假定提出了挑战.

量子强化学习在实时快速大规模数据分析以及通信服务优化上有良好的前景，因而其在大规模工业控制系统中的应用，可为大规模工业控制系统智能化面临的两个主要挑战提供解决方案.

5.2.2 复杂科学实验自动化控制

复杂科学实验需要严格、精密的自动化控制.以量子实验为例，量子计算机需要严格控制容错、信息丢失等误差，这些误差极其复杂，很难手动模拟排除.实现强大的量子计算必不可少的就是对量子进行门控制，以此来保证去除干扰的量子状态，保证正确的量子信息能够精确快速地通过控制门.控制量子门的算法往往不能达到量子计算机需要的精确度和速度要求.强化学习在控制优化问题上显现出很好的效果，可以从噪声控制轨迹中提炼非局部规律(Non-local regularities)，并在多种任务中进行迁移.为了将这些优势应用于量子控制优化问题上，谷歌的研究者提出了一种结合深度强化学习的控制框架[31]，可以同时优化量子计算的速度和精准性，以弥补泄露和随机控制错误带来的问题.

量子实验是在完全的量子环境中进行的，量子强化学习中量子交互式的学习方法(如量子元学习)给高效的量子容错计算、减少错误来源和可扩展的量子计算机实现提供了可能.量子强化学习方法的发展和在量子实验中的应用，将为通用量子控制机制提供额外的计算能力，促进量子计算能力全面的提升，也可以进一步促进量子强化学习在复杂科学实验自动化控制中的应用.

5.3 智慧城市

智慧城市旨在提供多种新型的、以人为中心的服务，以提高居民生活质量.智慧城市的实现，必须依赖量子技术、人工智能、物联网等新技术的发展进步.随着人工智能和物联网的发展，已经有许多以人为中心的智能服务出现，包括医疗保健、智能家居、城市交通网管理、城市联网报警及救援服务管理(火灾和洪水等情况)等.这些服务通过不同平台的实现已经成为可能，比如通过在城市大规模部署摄像头，可以加强城市安全；智能手机和多种可穿戴设备的传感能力，为医疗保健提供了基础.然而，综合一体化的智能服务体系还处于初步探索阶段.

在大型的智能城市服务系统中，利用量子强化学习技术可以同时提供超高的实时计算能力和对大规模数据的快速提取及分析能力，从而提供实时的智能决策.量子强化学习方法的发展，将极大促进智能化服务的发展进步.量子技术对强化学习不同任务的加速，将有助于实现多种多样的大数据分析应用和实时大数据流分析方法.量子强化学习在智能分析、实时决策和优化调度等方面的应用，将给智慧城市中的远程医疗、自动驾驶、智能家居、智能办公和医疗保健等领域提供很好的前景.量子强化学习研究的进一步深入，将极大推动绿色智慧城市的到来.

5.4 产业升级

量子强化学习的发展，给大量的行业带来效率提升、模式变革和产业升级的机遇.这些行业可能涉及经济和社会生活的方方面面，本节仅从三方面进行说明：①量子强化学习应用于量子实验控制，有望形成精确的分子行为模拟，会给化工产品生产、能源医疗保健等领域带来重大影响；②量子强化学习的快速适应能力，会给复杂的金融分析和快速决策带来希望；③量子强化学习同云计算结合，可以为智能量子云计算提供新的愿景.

5.4.1 利用精确的分子行为模拟以改善生产效率

量子强化学习方法同量子计算机的结合，将给分子行为模拟方面带来极大的升级.例如，该领域的发展将为肥料制造提供更有效的方法.几乎所有广泛应用的肥料都和氨的生产有关，更高效地生产氨(或替代物)意味着更低成本的肥料.然而，因为催化剂的可能组合数量是无限的，氨的制造工艺改进和替代氨的方法进展缓慢.而用今天的超级计算机，对氨的合成过程进行数字模拟测试，找出最优的催化剂组合来优化氨的生产过程，依然是无法完成的.量子强化学习方法，可对化学催化过程进行快速分析模拟，并采用基于模型的方法对可能的催化剂组合空间进行快速自动化探索，从而产生最优的催化剂组合.此外，量子强化学习结合量子控制机制，可有效地对自然界一种微小细菌存在的固氮酶分子进行模拟，进而给以非常低的能量成本生产氨提供了可能.同时，在气候变化预测、医疗保健、材料科学和能源等领域，通过精确模拟分子行为，将为这些领域带来重大提升.

5.4.2 金融服务

金融服务通常采用由市场和投资组合表现的概率和假设组成的算法，对投资方式进行决策.但是由于传统算法对于大规模数据快速实时分析的能力有限，在组合风险和欺诈检测上依然有很多问题.量子计算和机器学习方法的结合可以有效消除数据盲点，识别毫无根据的金融假设，以规避损失.量子强化学习将对复杂优化问题的解决提供良好的前景，对金融系统中投资组合风险优化和欺诈检测给出快速有效的结果.同时，基于模型的量子强化学习方法，可用于模拟金融交易系统，了解风险和不确定性对金融预测模型的影响，对投资组合进行并行模拟，快速有效地优化交易策略，为快速稳定的金融交易预测系统的实现提供了可能.

5.4.3 云计算

近年来，量子云计算成为云计算领域一个很好的前景.量子云平台可以简化编程，并提供对量子计算机的低成本访问.包括IBM、谷歌、阿里巴巴和华为等科技公司都对外开放了自己的量子计算平台.量子云计算是通过云调用量子仿真器、模拟器或处理器来进行计算任务.随着量子云计算的发展，云服务越来越被视为提供对量子计算机访问的可行方法，在量子计算教学、量子计算研究和量子游戏中的应用越来越多.基于量子强化学习，通过将量子化的智能体部署到量子云服务器上，可有效平衡云服务器的性能和开销，同时对服务器耗能等方面实现实时优化.

6 结 论

量子强化学习作为强化学习和量子计算的交叉研究领域，目前已经在多个方面取得了一定的研究进展.①利用量子计算并行性提供的强大算力，来实现对强化学习过程的加速；②基于量子机制特性和不断丰富的量子算法，很多研究提出了新的强化学习方法；③借鉴传统强化学习算法，提出新的量子力学研究方法.量子强化学习的研究进展虽然处于起步阶段，但现有成果已经给很多研究者带来了无限的憧憬.

量子计算同强化学习的融合发展，将极大地促进智能时代的发展进步.①量子强化学习对于物联网的安全隐私、实时智能交互、资源分配等方面有巨大潜力；②量子强化学习的发展，对于大规模工业控制系统的自动化和量子实验自动化控制的发展有重要意义；③量子计算同人工智能技术的融合，将促进以人为中心的绿色智慧城市的到来；④量子强化学习技术的深入研究，对于许多行业将产生重要影响，包括基于分子模拟的天气预测、化工生产、金融服务和云计算等行业.这些都将成为推动量子强化学习发展的内在动力.未来量子强化学习的研究将更加令人振奋，但同时有以下问题等待突破：首先，量子强化学习的研究和应用还处于初始阶段，还没有一个完备的理论框架出现；其次，对复杂任务环境进行量子化依然很困难；最后，在量子强化学习算法的设计方面，仅停留在理论方面，由于技术等方面的限制，还没有物理实验方案的实现.综上所述，量子强化学习的研究充满了挑战，同时也充满了无限的希望和可能性.