基于RecurDyn的澳洲坚果破壳装置最低转速的求解与验证*

潘睿，薛忠, 2，王槊，范建新，何凤萍，韩树全

(1. 中国热带农业科学院农业机械研究所，广东湛江，524091；2. 中国热带农业科学院南亚热带作物研究所，广东湛江，524091； 3. 贵州省农业科学院亚热带作物研究所，贵州兴义，562400)

0 引言

澳洲坚果果仁营养丰富[1-2]，与其他坚果相比其果壳结构致密坚硬，机械破壳确保果壳破碎且不损伤果仁是澳洲坚果加工技术的难点。近年来国内外学者针对澳洲坚果果壳的含水率、干燥特性、力学特性等已取得了较多的研究成果[3-9]。在澳洲坚果破壳技术方面，薛忠等[10-12]利用材料试验机对其进行壳果多因素压缩、剪切试验并开展了破壳机设计与试验；涂灿等[13]运用有限元方法对澳洲坚果的3个加载方向进行应力、应变分析，分析出较佳的破壳力方向；Fleck[14]通过试验表明澳洲坚果果径尺寸对破壳力的影响较小；Teh等[15]通过试验表明澳洲坚果果壳开裂需要2 240±430 N的力。由于国内澳洲坚果破壳工艺研究相对落后，大部分破壳设备需对澳洲坚果先分级再加工，目前主流加工方式一般为锯壳、挤压和剪切。锯壳方式导致澳洲坚果果壳高温产生焦油等有害物质的问题；挤压破壳存在果壳开口率低、果仁整仁率低的缺点；剪切破壳目前主要集中在手动及半自动破壳机械，存在效率低的现象。为提高澳洲坚果破壳效率，项目团队针对澳洲坚果果壳特性研制了一种无需对壳果分级、可连续加工作业，利用冲击和剪切破壳的全自动V型双通道澳洲坚果破壳装置，因实际作业时澳洲坚果果壳受力大小难以确定，因此应用RecurDyn软件对破壳关键部件进行仿真试验求解当满足破壳标准时破壳装置工作的最低转速。

RecurDyn(Recursive Dynamic)软件采用相对坐标系运动方程理论和完全递归算法求解存在复杂接触的多体系统动力学问题，可对破壳过程进行有限元模拟分析[16]。本文将基于RecurDyn软件对团队研制的V型双通道澳洲坚果破壳装置[17]进行显式动力学分析；通过分析破壳刀片对果壳施加的剪切力大小及应力分布情况，求解破壳装置最低工作转速；通过样机试验验证仿真结果并得出刀盘轴转速对破壳率的影响，为进一步提高破壳装置破壳率提供理论依据。

1 试验设备及方法

1.1 澳洲坚果破壳装置的结构特点与工作原理

为提高澳洲坚果破壳作业质量，设计如图1所示的澳洲坚果破壳装置，主要由刀盘、左右破壳腔、刀盘轴、动刀刀片、定刀刀片、刀具固定楔块等组成。左右破壳腔通过螺栓固定于弧形背板，紧固在刀盘轴上的刀盘随刀盘轴转动而旋转，为防止滚动轴承松动在刀盘轴右侧安装止动螺母。

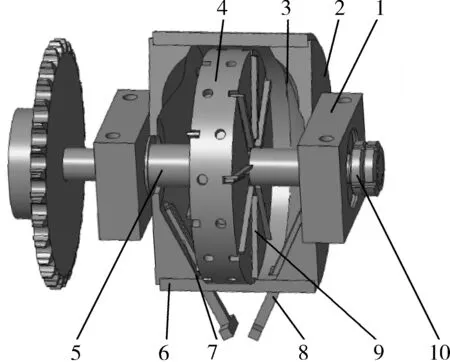
图1 破壳装置Fig. 1 Shell breaking device1.轴承座 2.侧面板 3.破壳腔 4.刀盘 5.刀盘轴6.弧形背板 7.定刀刀片 8.定刀楔块 9.动刀刀片 10.止动螺母

定刀刀片、动刀刀片均为厚约2.4 mm的等腰梯形棱柱，刀片材质为钨系高速钢，热处理后其硬度需达到HRC62-65。定刀刀片通过刀具固定楔块紧固在破壳腔刀槽，当澳洲坚果运动至其位置时对其果壳施加剪切力和冲击力。破壳装置中左右两侧破壳腔被刀盘均分为两部分形成双通道，刀盘左右两侧设计了以45°均布的动刀刀槽，分别紧固8组动刀刀片及固定楔块，强制破壳腔内的澳洲坚果作圆周运动，为满足刀盘工作动平衡在其侧壁设计了凹陷圆孔，如图2所示。

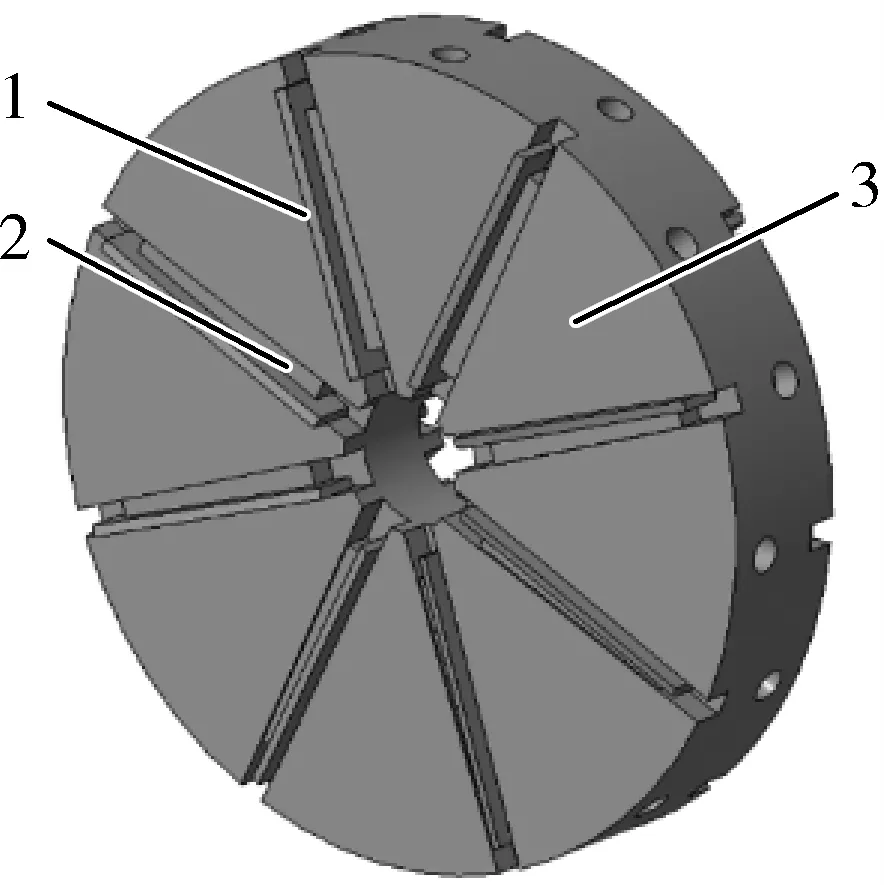
图2 刀盘结构示意图Fig. 2 Schematic diagram of cutter head structure1.动刀刀片 2.动刀楔块 3.刀盘

破壳腔结构如图3所示。左右破壳腔用于容纳喂入的澳洲坚果，破壳腔上半部分的凹槽可防止喂入口堵塞，下半部分的方槽用于固定定刀刀片，可根据需要改变刀片伸出高度。

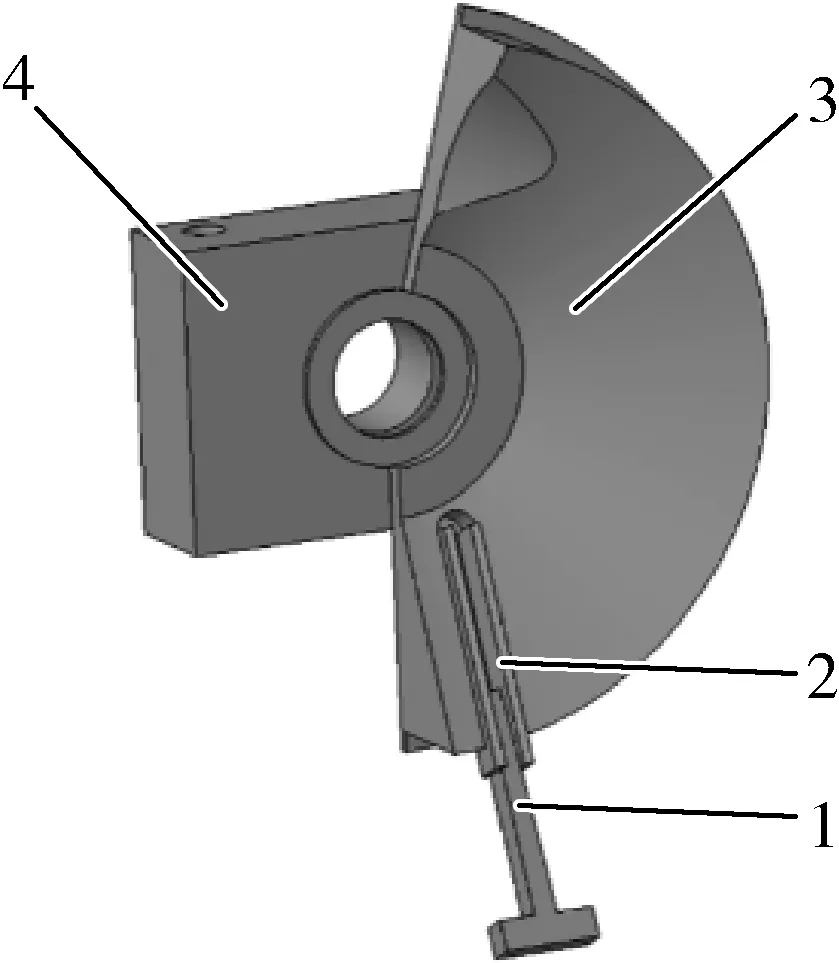
图3 破壳腔结构示意图Fig. 3 Schematic diagram of the shell cavity structure1.定刀楔块 2.定刀刀片 3.破壳室 4.轴承座

破壳作业时电机驱动刀盘轴旋转，澳洲坚果由导料滑轨分别滑入左右破壳腔，动刀强制澳洲坚果运动与定刀相遇形成冲击破壳作用并由V型间隙产生剪切、挤压作用，果壳破碎后的混合物由动刀排出破壳室，达到破壳取仁的目的。与传统澳洲坚果破壳机相比，该破壳装置破壳腔内壁设计有光滑凹面防止澳洲坚果堵塞；两组定刀刀片分别通过刀具固定楔块紧固在左右破壳腔刀槽中，与动刀刀片形成了无漏、防堵塞、夹角为30°的V型间隙，保证澳洲坚果喂入和破壳作业的顺畅进行，如图4所示。

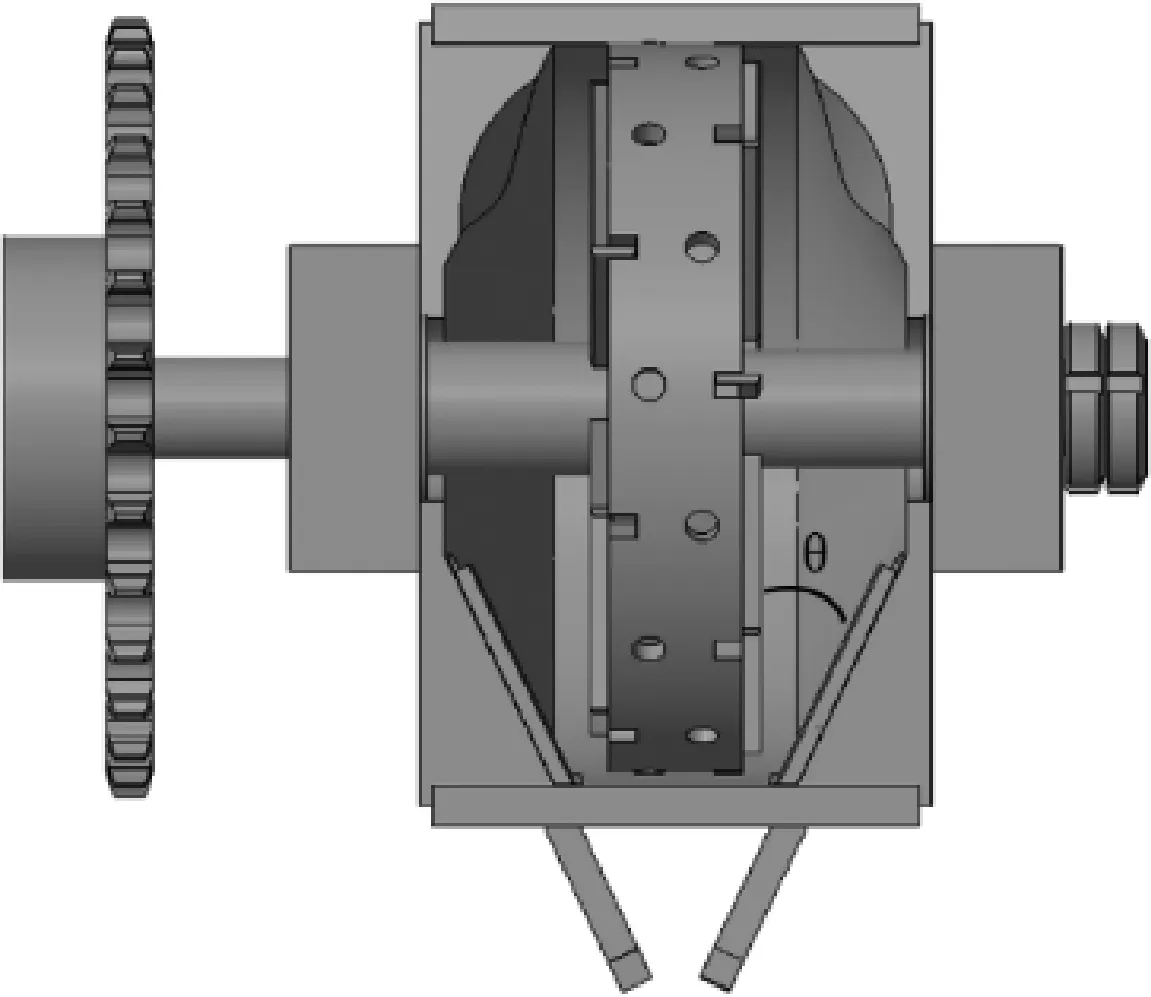
图4 破壳装置V型间隙示意图Fig. 4 Schematic diagram of V-shaped gap ofshell breaking device

1.2 试验方法

1.2.1 澳洲坚果主要破壳参数确定

当澳洲坚果含水率较高时，果壳内部壳仁粘结成一体，食用效果不佳且破壳作业易将果仁切碎，因此破壳加工前将坚果烘干至一定含水率使其壳仁分离后破壳效果更好。果壳截面模型如图5所示，果壳受力情况主要受果壳破碎极限、刀具对果壳破碎的最小剪切力、果壳厚度等物理力学特性影响。

图5 澳洲坚果建模截面Fig. 5 Macadamia nut modeling cross section

当动刀带动澳洲坚果运动与定刀形成V型间隙时，澳洲坚果受到的剪切力分析示意图如图6所示。

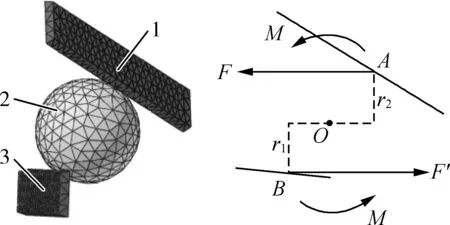
图6 澳洲坚果受到的剪切力Fig. 6 Shear forces on macadamia nut1.动刀刀片 2.澳洲坚果 3.定刀刀片

刀片形成V型间隙时分别在澳洲坚果两点产生剪切力F、F′，两受力点与球心间力臂长度分别为r1、r2，当r1=r2时，F、F′大小相等，形成力偶矩M，刀片对坚果产生的扭矩T与力偶矩M大小相等，由于刀片伸出部分高度ρ约4.5 mm，求得r1、r2之和约为15 mm。

根据澳洲坚果受到的扭矩和极惯性矩的关系，最低破壳剪切力的计算如式(1)。

(1)

式中：τP——坚果受到的切应力，MPa；

ρ——刀具最外侧伸出端高度，mm；

[σ]——坚果的破碎极限，MPa；

IP——坚果的极惯性矩，mm4；

α——坚果果壳内外径之比；

d——果壳内径，mm；

D——果壳外径，mm。

根据式(1)，澳洲坚果破碎的最小剪切力

(2)

由于澳洲坚果果壳为脆性材料，因此该模型满足Tresca[18]屈服准则。

σ1-σ3≤[σ]

(3)

式中：σ1——材料在复杂应力状态下的最大主应力；

σ3——材料在复杂应力状态下的最小主应力；

σ1-σ3——当量应力。

澳洲坚果直径一般为24～26 mm，因此选用25 mm 直径澳洲坚果为研究对象，进行20组剪切破碎试验，试验结果表明其最大破碎极限[σ]约为2.7 MPa；参考文献[19]可知，澳洲坚果果壳顶部厚度约为4.03～4.36 mm，中底部壳厚为2.22～2.48 mm，即α约为0.715～0.74，取中间值0.727 5；π取3.14，求得最小破壳剪切力1 103.73 N。澳洲坚果模型的主要参数取值如表1所示。由于果壳不同位置厚度不均，存在各向异性，因此果壳不同位置弹性模量大小不一。由于破壳过程中刀片对果壳切口位置随机，不同方向所需破壳力不同，为方便计算，假定果壳各方向弹性模量各向同性，取最大值约68.63 MPa，即仿真试验中各方向果壳所受剪切力大小一致。

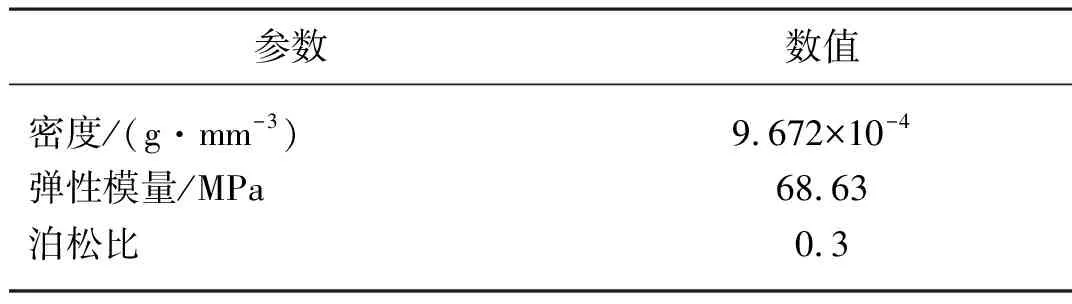
表1 澳洲坚果的材料参数Tab. 1 Macadamia nut material parameters

1.2.2 有限元分析

1) 破壳装置的有限元模型。RecurDyn软件中包含建模功能，但是对复杂实体模型建模相对困难，一般借助Cad软件实现建模。破壳装置结构相对复杂，因此在Creo软件中创建破壳装置三维实体模型，将文件保存为x_t格式文件并导入RecurDyn软件中进行网络划分。本研究将模型简化处理，采用自由网格划分网络，澳洲坚果及刀片的网格大小分别为3 mm、2.5 mm，其网格数量分别为1 927和571，如图7所示。

(a) 澳洲坚果

(b) 刀片图7 澳洲坚果及刀片简化模型Fig. 7 Simplified model of macadamia nut and blade

2) 仿真模型参数设定。破壳装置尺寸较复杂，根据RecurDyn软件计算特点，对仿真模型参数设定如下：(1)破壳装置及澳洲坚果模型的三维实体单元定义为Solid4_1，定义破壳装置模型材料为塑性材料模型Plastic/Isotropic，材料弹性模量为2.1×105MPa，密度为8.7×10-3g/mm3，泊松比为0.3。(2)在破壳过程中，澳洲坚果由导料滑轨滑落，自由落体至破壳腔内，因此破壳装置与澳洲坚果无初始接触，应将二者尽可能靠近以减少澳洲坚果进入破壳腔前的空余计算时间。(3)定义破壳装置模型的初始速度：刀盘轴绕Z轴(刀盘轴方向)的旋转速度为100～500 r/min，以便反映在不同转速下澳洲坚果模型受到的应力应变。

3) 破壳过程仿真。随着刀盘轴转动，澳洲坚果在刀片的错位剪切作用下，果壳与刀片接触点处最先开始变形；随着刀盘轴继续转动，刀盘内侧面挤压澳洲坚果，果壳变形逐渐增大并断裂，在刀盘内侧面挤压和刀片剪切的双重作用下迅速破坏。定刀、动刀对澳洲坚果剪切破壳的局部放大图如图8所示，可清晰显示果壳变形趋势。

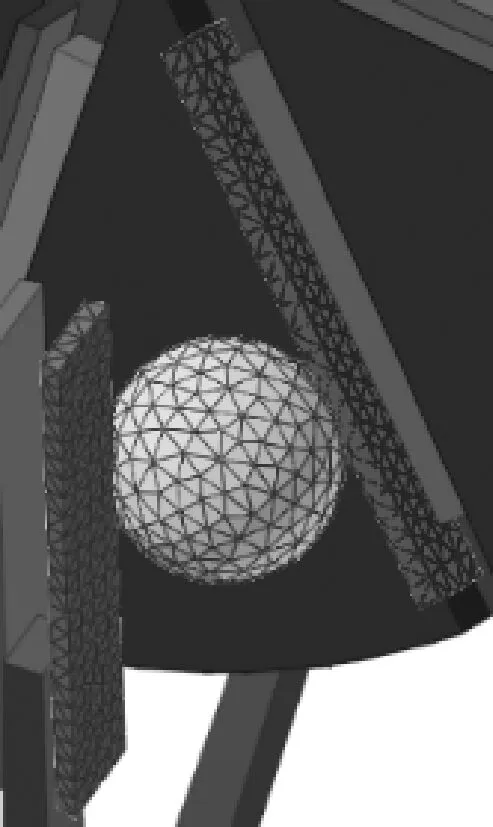
(a) 0.086 25 s

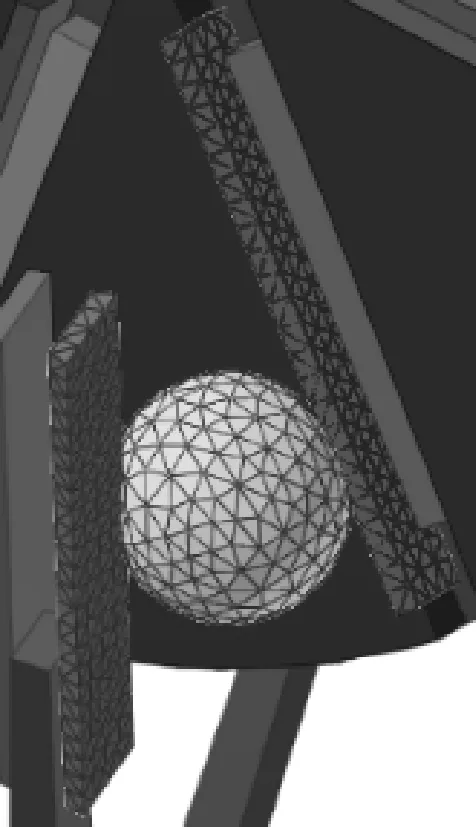
(b) 0.087 75 s

(c) 0.089 25 s

(d) 0.090 75 s图8 破壳过程局部图Fig. 8 Partially enlarged group picture of theshell breaking process

2 结果与讨论

刀盘轴转速将决定澳洲坚果在破壳腔中是否完全破碎，同时决定刀具是否发生弯曲变形等情况，进而影响破壳作业。根据该装置设计的实际情况，设定刀盘轴初始转速为100 r/min，每组试验转速增加10 r/min，共进行41组仿真试验，试验结果如图9所示。

根据动量定理

F·Δt=m·Δv

(4)

式中：F——澳洲坚果所受剪切力；

Δt——果壳与刀片作用时间；

m——坚果质量；

Δv——坚果在破壳装置中的速度变化。

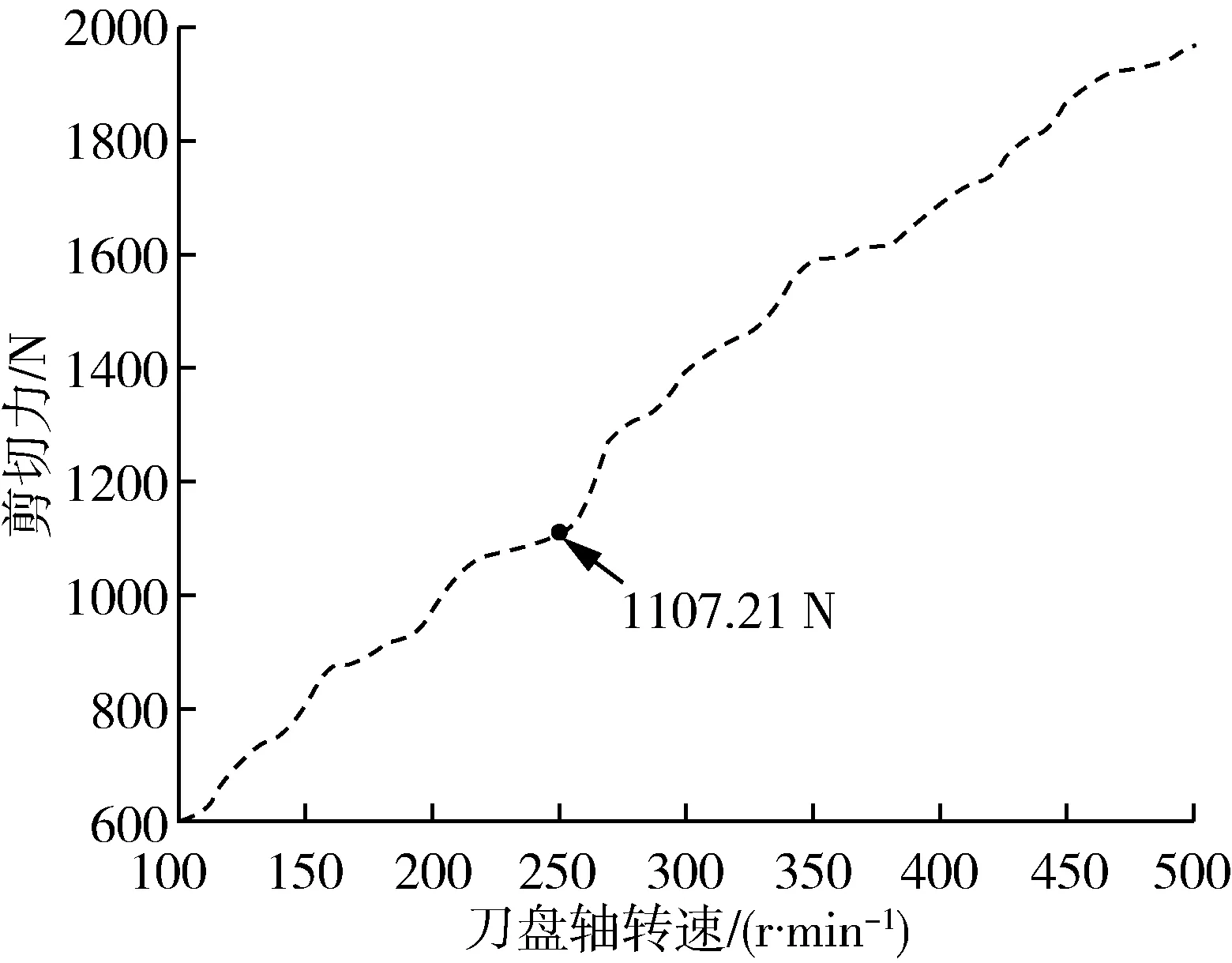
图9 仿真试验中不同转速下果壳所受剪切力Fig. 9 Shear force on the husk at different speeds in thesimulation experiment

分析图9数据可知，由动刀强制进行圆周运动的澳洲坚果的线速度随刀盘轴转速增加而增大，因此刀盘轴转速越大，即Δv越大；Δt作为果壳与刀片的作用时间数值极小，可忽略不计。因此，当澳洲坚果质量一定时，其果壳所受剪切力随刀盘轴转速增加而增大。

由式(2)计算得的最小破壳剪切力1 103.73 N，当刀盘转速为250 r/min时，刀具对澳洲坚果产生的剪切力首次高于1 103.73 N，此时果壳受到剪切力为1 107.21 N。

定刀、动刀的应力、应变、变形量云图如图10、图11所示。由图分析可知，刀盘轴转速为250 r/min时定刀受最大应力为46.9 MPa，应变为1.94×10-4，变形位移量为9.19×10-4mm；动刀受最大应力为53.4 MPa，应变为2.21×10-4，变形位移量为1.05×10-3mm。刀片材料为W18Cr4V，其抗弯强度一般大于300 MPa，远大于所受最大应力。定刀、动刀的应力、应变最大处均位于与果壳发生剪切作用的刀刃处，应力、应变最大处到固定刀槽槽口的受力及变形过渡性较好且未发生明显突变，说明刀盘结构设计合理，刀片受力变形较小且未发生扭转变形。澳洲坚果的应力、应变和变形云图如图12所示。根据图12分析得出，刀盘轴转速为250 r/min时果壳受最大应力为16.1 MPa，应变为0.203，大于果壳强度极限，能够满足破壳需求。澳洲坚果在两侧刀具剪切点处变形最大，向外变形逐渐变小，裂纹有明显走向。

(a) 应力云图

(b) 应变云图

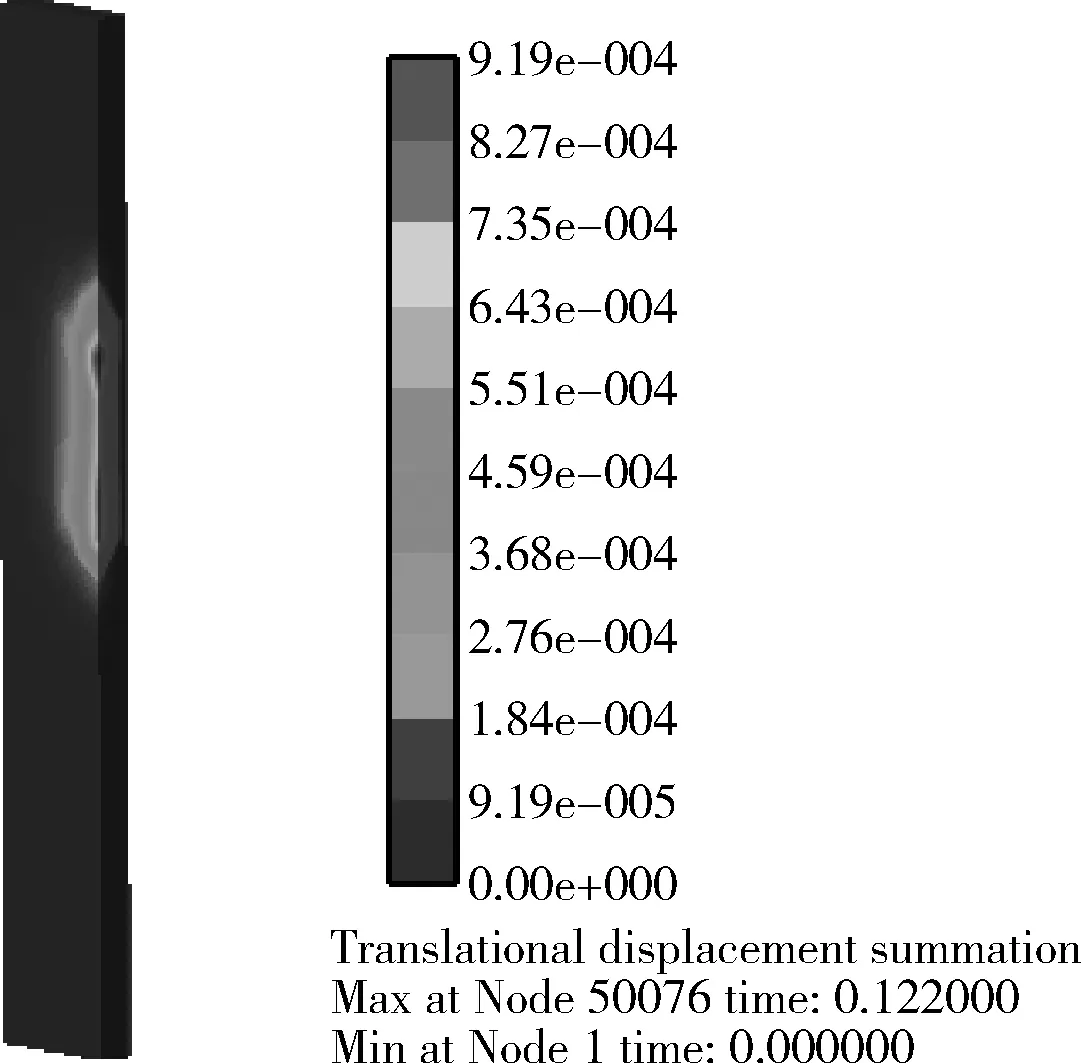
(c) 变形云图图10 刀盘轴转速为250 r/min时定刀的应力、应变和变形云图Fig. 10 Stress, strain and deformation clouddiagram of the fixed knife at 250 r/min

(a) 应力云图

(b) 应变云图

(c) 变形云图图11 刀盘轴转速为250 r/min时动刀的应力、应变和变形云图Fig. 11 Stress, strain and deformation clouddiagram of the moving knife at 250 r/min

(a) 应力云图

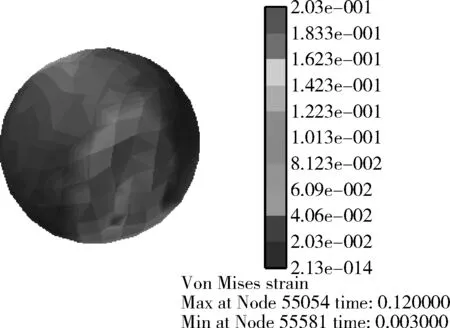
(b) 应变云图

(c) 变形云图图12 刀盘转速为250 r/min时澳洲坚果的应力、应变和变形云图Fig. 12 Stress, strain and deformation clouddiagram of macadamia nut at 250 r/min

通过以上分析可知：定刀、动刀应力最大处应变也最大，在刀具固定楔块的作用下最大应力应变处的变形量较小，说明该结构中刀具扭转变形和断裂的可能性较小。刀片对澳洲坚果产生的剪切力及澳洲坚果受到的最大应力、应变随刀盘转速提高而增大。当刀盘轴转速为250 r/min时，刀具对澳洲坚果产生的最大应力大于果壳的强度极限，澳洲坚果受到的剪切力为1 107.21 N，大于最小破壳剪切力1 103.73 N，因此该破壳装置有效破壳的最低转速为250 r/min。

3 样机试验与结果分析

为验证澳洲坚果破壳装置最低工作转速仿真试验结果与样机试验的差异以及研究不同刀盘转速对澳洲坚果破壳率的影响，试制样机并进行试验。

3.1 试验设备及材料

选用经干燥含水率为2%～5%的澳洲坚果作为试验材料。试制澳洲坚果破壳装置样机如图13所示。试验用工具包括游标卡尺、电子秤、秒表等。

图13 澳洲坚果破壳样机Fig. 13 Macadamia nut shelling device prototype

3.2 试验方案及评价指标

为测定不同转速下破壳装置样机的破壳率，试验设定刀盘轴初始转速为100 r/min，每组试验转速递增10 r/min，最高转速为500 r/min。每组试验选用澳洲坚果200个，测定试验后破壳效果满足要求的坚果个数，共进行5次试验并对其结果取平均值。根据以下计算方法求出相应指标数据。

破壳率指破壳试验后果壳破碎露出果仁的坚果个数占每次试验坚果总个数的百分率。

(5)

式中：S——破壳率/%；

h——满足要求的破壳坚果个数；

H——喂入坚果的总个数。

根据试验结果测定的破壳率越高则表明破壳装置对澳洲坚果破壳效果越好。

3.3 试验结果与分析

破壳试验过程如图14所示，不同转速下破壳装置样机的破壳率结果如图15所示。

分析数据得知当刀盘轴最低转速为100 r/min、最高转速为500 r/min时，破壳装置样机的破壳率处于66.7%～96.74%，破壳率随刀盘轴转速提高而增长。当刀盘轴转速低于250 r/min时，部分坚果出现从V型间隙漏出未破壳的现象，导致破壳率较低；当刀盘轴转速为250 r/min或更高时，坚果漏出现象明显减少，破壳率高于90%。随着刀盘轴转速提高，破壳率处上升趋势且趋于平缓，因此破壳装置满足破壳需求的最低工作转速为250 r/min，刀盘轴转速为250～500 r/min时破壳装置破壳率为92.6%～96.74%。

图14 破壳装置样机破壳试验Fig. 14 Shell breaking test of the shell breaking device prototype

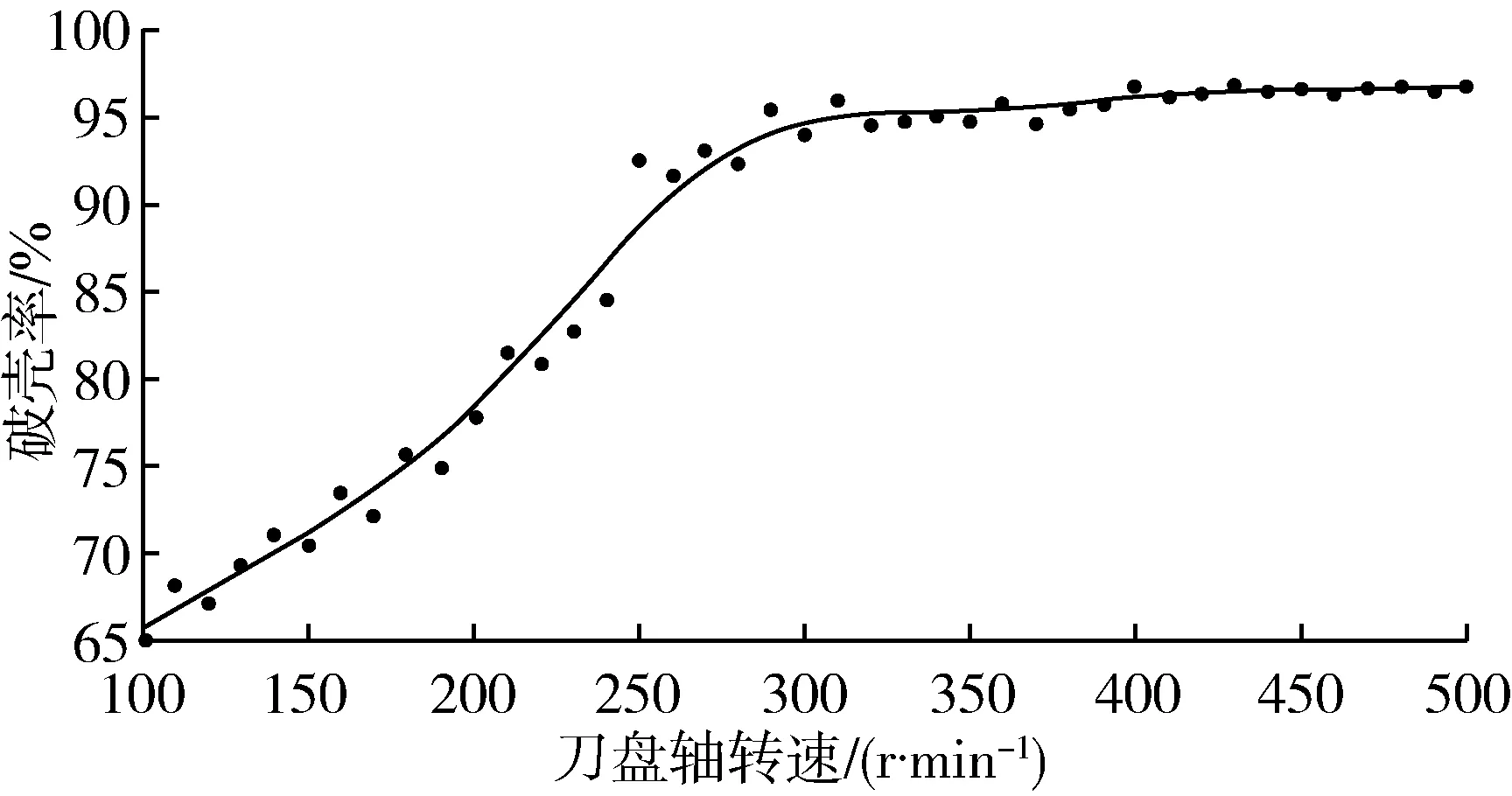
图15 破壳装置破壳率Fig. 15 Shell breaking rate determined by shell breaking test

4 结论

本文利用RecurDyn软件对澳洲坚果破壳装置破壳过程进行数值模拟分析，通过样机试验得到以下结论。

1) 通过仿真试验验证该破壳装置中刀片扭转变形和断裂的可能性较小。刀片对澳洲坚果产生的剪切力随刀盘轴转速提高而增大，刀盘轴最低转速为250 r/min 时可满足破壳需求。

2) 试制澳洲坚果破壳装置，以刀盘轴转速为100～500 r/min进行破壳试验。试验结果表明破壳率随刀盘轴转速提高而增长，样机破壳率为65.7%～96.74%。当工作转速低于250 r/min时，部分坚果从V型间隙漏出；当刀盘轴转速为250 r/min或更高时，坚果漏出现象明显减少，破壳率高于90%。因此确定破壳装置满足破壳效果的最低工作转速为250 r/min。工作转速为250～500 r/min时破壳装置破壳率为92.6%～96.74%。