例谈学生数学概念深度学习的影响因素

王园园 吕露青

摘   要：深度学习利于学生更好地把握所学知识内容的核心，掌握数学概念的本质。数学概念深度学习需要学生经历概念的形成过程，其学习过程受学生已有知识经验、丰富典型例证、教师关键问题引导、有效练习形式等诸多因素影响。在教学中要予以关注，采取恰当合理的教学方式，促进学生深度学习，提升学生核心素养。

关键词：小学数学;数学概念;深度学习;影响因素

中图分类号：G623.5   文献标识码：A   文章编号：1009-010X（2021）16-0031-04

数学概念是学生数学学习的重要组成部分，它既是数学学习的逻辑起点，也是数学思维的核心。深度学习使得学生更好地掌握数学概念的本质，把握所学知识内容的核心，促进学生关键能力与核心素养的发展。概念深度学习需要学生经历概念的形成过程，其学习过程受学习者、教育者及学习环境等诸多方面的影响，在实践中我们发现学生已有经验、丰富典型例证、关键问题引导与练习设计形式对学生数学概念深度学习起着重要作用，本文将结合课例来谈这几方面因素的影响。

一、学生已有经验

一般来说，数学概念源于两方面：一方面是人们对客观生活经验的总结及数量关系和逻辑关系的推导;另一方面则是在已有的数学知识基础上进一步建构。这就决定了学生已有的生活经验和知识经验对促进概念的深度学习起着至关重要的作用。

丰富的生活经验和基础，直接影响学生对概念的学习。小学生并非一张白纸，他们在生活中已经形成了丰富的经验，不管是对自然现象还是对社会生活，他们都有了自己的看法和理解，这些经验、信息等被称为“前概念”。教师要善于把数学概念与学生生活经验形成的“前概念”联系起来，加深他们对数学概念的理解。在教学“相邻数”这一概念时，学生已经知道了“邻居”一词，可以借助“邻居”这一生活经验来理解“相邻”的含义，并让学生通过排队找一找谁与自己相邻，从而理解比一个数“多1”和“少1”的数，都是这个数的相邻数。

学生在理解和掌握新概念时，原有的知识经验越丰富，学习就会越容易。教学中要在学生已有的概念基础上，帮助学生找到新旧概念的“连结点”，引入新概念。在学习“质数和合数”时，先让学生找出1～20各数的因数，然后引导学生观察，并根据因数的个数进行分类，在分类基础上引出质数和合数的概念。在复习旧知识的同时，又强化了新旧知识的内在联系，利于学生形成较为完整的概念体系。

二、典型丰富例证

“角的认识”一课通过提供不同角度、不同开口方向摆放的各种典型情况帮助学生认识角。首先，通过红领巾的角、数学书封面的角、桌面的角等静态角进行观察，建立对角的初步认识。然后，通过折扇开合、剪刀打开、钟表指针转动等动态角的呈现来观察角的大小变化，帮助学生理解“角的大小与边的长短无关，与张口大小有关”。通过“静”与“动”的典型例证深化“角”概念的本质，有利于学生对概念形成深刻、全面的理解，这种典型的例证能让概念本质属性更加突出，促进数学概念的建构和深化。由此可见，小学生对于抽象的数学概念的理解需要依赖典型例证。

学习材料的数量多少也会影响小学生数学概念学习。在“小数的意义”教学时，借助人民币、米尺、正方形、正方体、数线模型等不同形式的丰富例证进行抽象概括，充分理解小数的意义，直观感受由单位不断细分产生小数的过程，以及相邻两个计数单位之间的十进关系，培养学生的迁移和类推能力，使学生对小数的意义理解更深刻。如果学习材料的数量太少，学生感知不充分，就不能获得有关概念应有的表象;数量太多，无关属性将干扰对概念本质属性的认识，从而影响数学概念的建构。因此，丰富恰当的例证能让学生充分感知，获得有关概念的应有表象，抽取各种对象的本质属性。

三、关键问题引导

教学重在引导，学习贵在思考。深度学习是教师充分发挥主导作用的活动，通过适当的引导，使学生实現由知识层面到思维层面的提升。教师要在深刻理解概念、把握知识联系的基础上，设计具有思考力的关键问题，引发学生自主探究，促使学生更深入地思考。

如教学“长方体的认识”时，教师设计以下问题引导学生研究长方体的特征。

问题1：长方体面、棱、顶点有什么特点？

通过小组合作，观察手中的长方体，并完成任务单。

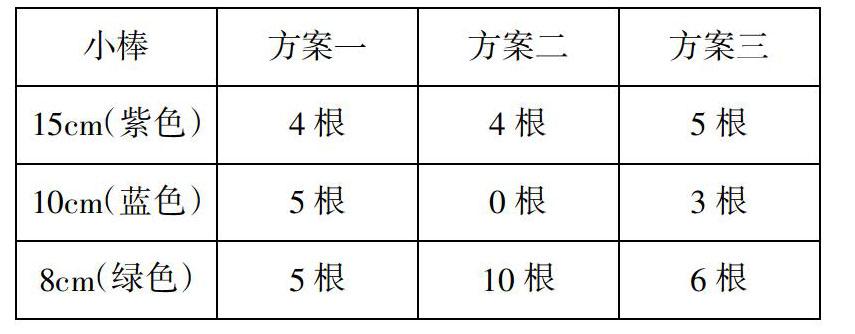
问题：2：用小棒怎样搭建长方体框架？

提供如下三种方案，先思考每种方案能否搭成，再选取相应方案动手搭一搭。

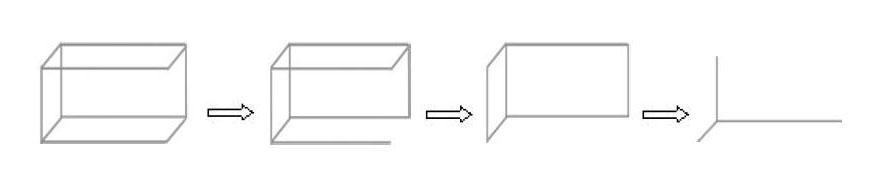
问题3：搭建长方体方案三缺少一根，能想象出搭成的样子吗？至少剩哪几根仍然能想象出撘成的样子？动手拆一拆。

教师对关键问题的引导，如同引擎般将学生“发动”起来，动手体验、思考探究，不断深化长方体特征的认识。填一填：让学生在观察、比较、分析等实践活动中，凸显知识的形成过程;搭一搭：动手操作前动脑，动手操作中思考，学生选择搭建材料就是深化长方体特征的过程;拆一拆：边拆边想象长方体原来的样子，最终发现相交于同一顶点的三条棱：长、宽、高，是决定长方体大小、形状的关键信息，学生的思维在“问题链”中不断深入。

“关键问题”除了体现于课堂整体设计的大问题，还应关注细节的引导，通过追问、反问与提出新的问题促进学生的不断思考。如教学“分数的意义”时，学生在理解单位“1”后，教师通过有针对性的追问：①表示什么含义？②表示什么含义？③的含义呢？帮助学生逐渐抽象，引导学生经历概念的形成过程，借助模型充分理解分数的意义，由表及里深化概念的掌握。

四、练习设计形式

课堂练习是教学的重要组成部分，对概念深度学习有着举足轻重的作用。学生初步形成的概念，需要通过多形式多层次的练习加以巩固深化。其中，“对比”和“变式”的练习形式，能让学生在分析、比较中进一步强化对概念的理解和掌握，有利于促进概念深度学习。

对比练习就是在“异”与“同”的比较中凸显概念本质。著名教育学家乌申斯基说过“比较是一切理解和思维的基础。”教学中通过设计对比练习，突出概念之间的区别和联系，学生在比较中提升辨析事物本质的能力，准确掌握数学概念的本质特征。在“长方形和正方形的认识”练习中，设计“送图形宝宝回家”的题目（如下图）。首先，学生把图形宝宝送回家，需要对比长方形和正方形的不同特征，对概念掌握更清晰;然后，让学生思考：正方形能否住进长方形的家？学生通过比较两个概念的特征，打通了长方形和正方形之间的联系。通过对比练习使概念在比较中得到巩固拓展，灵活运用。

变式练习使学生在题目变化中深入分析，深化概念的内涵，使学生在事物的各种表现形式中认识事物的本质属性。教学中有针对性的变式练习，通过变换概念的非本质属性，让学生在不同情境中对概念的认识更深刻、更概括。

如“倍的认识”设计一系列的变式题目，进一步加深“倍”的理解。

变式一（标准量不变，比较量发生变化）：

分组依次出示课件，分别让学生说一说每组中梨的个数是苹果的几倍，通过变化梨的个数，让学生观察变化后两者间倍数关系有什么变化。发现：标准量不变，比较量发生变化，倍数也随着发生变化。

变式二（比较量不变，标准量发生变化）：

本题有意设计每组中梨的个数始终不变，苹果的个数不断发生变化，再观察梨的个数是苹果个数的几倍，思考：梨的个数没有发生变化，为什么它们的倍数关系却发生变化呢？发现：标准量变化，比较量不变，倍数关系也跟着发生变化。促使学生思考概括，研究倍数关系关键在于找准标准量，有几个这样的标准量就是它的几倍。通过这样的变式练习，不仅加深了学生对倍的理解，还培养了学生思考问题的深刻性和全面性。

变式三（从实物抽象到图形）：

本环节通过苹果和梨的实物过渡到长方形，再到抽象成线段，让学生经历从实物到图形，从直观思维向抽象思维过渡的思维发展过程，借助多元表征，在对学習素材比较探索中促进学生真正的观察、发现、深化对概念的理解，帮助学生建立起倍的思维模型，实现“倍”的量性特征。

总之，在教学中要关注数学概念深度学习的影响因素，结合学生已有知识经验，呈现丰富典型的例证，教师通过关键问题引导学生深入思考，设计有效的练习形式，采取恰当合理的教学方法，促进学生深入思考，实现学生深度学习。

参考文献：

[1]马云鹏，吴正宪.深度学习：走向核心素养（学科教学指南·小学数学）[M].北京：教育科学出版社，2019.

[2]刘月霞，郭   华.深度学习：走向核心素养（理论普及读本）[M].北京：教育科学出版社，2019.

[3]吴正宪，刘劲苓，刘克臣.小学数学教学基本概念解读[M]. 北京：教育科学出版社，2014.

[4]张兴华.儿童学习心理与小学数学教学[M].南京：江苏教育出版社，2011.