考虑LIFO约束的2L-CVRP优化

尚正阳，顾寄南，潘家保

(1.安徽工程大学 机械与汽车工程学院，安徽 芜湖 241000；2.江苏大学 机械工程学院，江苏 镇江 212000)

0 引言

基于广泛的服务对象与客户需求，我国电子商务已于2019年突破30万亿元规模[1]，高效低耗的物流网络运行是提升社会经济效益的重要手段。现阶段，信息技术、交通运输与包装工程的快速发展，为精准的配送过程管控提供了硬件支撑，也为实施系统的物流调度优化创造了条件。考虑装载约束的路径优化问题模拟了现实配送行为，旨在同时满足货物装载与车辆载重约束，实现整体路径最短。根据不同货物属性，装载状态可分为二维与三维两种类型，本文针对二维装载约束下的车辆路径问题(Two-Dimensional Loading Capacitated Vehicle Routing Problem, 2L-CVRP)展开研究。

2L-CVRP是在带容量约束的车辆路径问题(Capacitated Vehicle Routing Problem, CVRP)中增加了货物装载约束，需要不断地调用二维装箱问题(Two-Dimensional Bin Packing Problem, 2BPP)模块，进行相应的填充可行性验证，它是基于CVRP与2BPP组合的NP-hard调度问题[2]。2007年，IORI等[3]最先研究2L-CVRP，并从路径寻优与装箱验证两个方面分别提出了分支切割(branch-and-cut)与分支定界(branch-and-bound)方法，完成了求解算法构建。这种两相式的算法构造策略，明确了2L-CVRP研究内容，得到了后续学者的广泛使用。

由于车辆载重与容积的双重约束，致使迭代过程易于陷入局部较优解，需要更为精准的寻优操作方法。GENDREAU等[4]在禁忌搜索的寻优框架下，设计了不同配送序列的邻域变换方式;LEUNG等[5]与RUAN等[6]分别将模拟退火与蜜蜂交配算法引入其中;DOMINGUEZ等[7]结合经典的路径优化Saving方法[8]，提出了具有导向性的随机搜索操作;LEUNG等[9]在传统禁忌搜索中加入了引导机制，能够有效帮助算法跳出局部较优解;WEI等[10]归纳了2L-CVRP的邻域搜索结构，将其分为序列内与序列间的因子插入、交换与倒置操作，同时给出了“先评价，后装载”的算法加速策略，以减少多约束条件下的装箱效果验证次数。着重于寻优算法的求解性能提升，WEI等[11]改变了退火温度迭代方式，发展了具有反复“升温”功能的模拟退火算法。现阶段，针对2L-CVRP的寻优过程改进，主要集中于多约束条件下的全局搜索能力提升与多模块耦合的算法运行效率增加两个方面。为此，需要更进一步的元启发式方法设计与整体算法构造。

装载验证贯穿于2L-CVRP的整个优化过程，是影响算法性能与效率的关键。区别于定量的车辆数、载重与起始点约束，装箱效果需要独立的2BPP运算。早期的效果验证充分借鉴了装箱理论方法，文献[9]整合了6种经典装箱策略：放置空间最左、放置空间最下、最大接触面积、不包括载具边缘的最大接触面积、最少占用矩形面积和最大适应度方法，进行逐次的空间放置选优。为适应3L-CVRP的高效求解，TAO等[12]通过引入最少空间浪费和最多接触面积的方法，设计了基于空间角点与相交边的适应度生成规则。然而，考虑到反复的装箱模块调用与“后进入，先卸载”(Last In First Out，LIFO)约束，简单的装箱方法迁移并不适用于2L-CVRP的高效求解。文献[10]改进了WEI等[13]所提出的空间格局评价方法，通过定量的位置参数计算，得出精准的放置效果适应度，其中skyline表示箱子的可能放置位置。基于容器剩余空间的格局判定[14]，文献[11]以箱子放置后的可用矩形数量作为适应度，建立了相应的MOS(maximal open space)生成方法。作为新兴载运模型下的2L-CVRP研究，当前仍缺少成熟的LIFO装载方法设计。虽然简单的2BPP策略迁移能够达到不错的求解效果，但是过于繁琐的求解过程并不适合于整体算法的反复调用。同时，相关文献并未给出装箱方法的具体操作，难以进行准确的参考研究与算法复现。

目前，国内关于CVRP与BPP联合优化的文献报道相对较少。王超等[15]在PISINGER[16]的装箱方法上加入了重力约束与层深度修正线，结合禁忌搜索提出了多阶段/两层的混合求解算法;颜瑞等[17]针对3L-CVRP，引用文献[9]中的6种顺序装箱规则，发展了具有禁忌搜索功能(记忆库)的改进遗传算法；针对2L-CVRP，颜瑞等[18]分别设计了基于最小浪费原则的装箱规则与量子粒子群算法搜索算法，其中装箱规则不包含LIFO约束，是对skyline方法[19]的简化。尚正阳等[20]通过CVRP及其衍生问题的求解特点分析，提出基于模拟退火操作的整体算法构建框架，明确了相关问题优化思路。总的来看，国内研究多集中于寻优算法改进，缺少系统的装箱方法及其执行策略设计。实际上，基础的装箱理论与优化方法开发仍是国内相关问题研究的软肋。

本文针对LIFO约束下的2L-CVRP展开研究，重点提出最少开放空间(Least Open Space, LOS)的二维装箱验证方法。LOS装箱方法能够以所构造的skyline数量为适应度，快速评价箱子的放置效果，运行高效且结构简单。同时，给出了具体skyline的生成策略与步骤，结合文献[20]中带有回火操作的模拟退火(Improved Simulated Annealing, ISA)求解框架，完成相应的加速策略设计与ISA-LOS算法构建。通过国际经典算例实验，解析并验证了所提算法的可行性与高效性，能够为相关的载运、装箱问题研究提供参考。

1 问题描述

2L-CVRP的实质是基于载重约束与装载约束的路径优化问题，具体实例如图1所示。已知不同客户的货物数量、重量和尺寸需求，以及其空间位置坐标，旨在基于给定的中心仓库位置与配送车辆属性，规划货物的装载方式与运输路径，实现总体路径最短。其中车辆属性包括车辆数量、载重能力和面积容积。参考文献[11]中的经典问题描述方法，其可行解需要满足以下条件：

(1)每个矩形货物必须与容器正交放置；

(2)货物之间不能干涉；

(3)车辆的载重与长宽不能超出使用，即载运货物不能超重和超出车辆容积；

(4)每个客户的货物需求都必须被一次满足，不能分批多次运输；

(5)在给定数量的运输车辆下，所有客户都必须被服务到；

(6)每一条路径的起始点与结束点都必须是中心仓库。

考虑不同类型的货物放置方式，引入旋转约束与LIFO约束。旋转约束表示货物可以旋转90°放置，而LIFO约束则表示所需货物能够在不移动其他货物的情况下直接卸载，减少额外配送操作，提高货物载运效率。如图1所示，货物不可旋转放置，且先配送客户1的货物在容器最外端，后配送客户4的货物在容器最内端，每次卸载互不干涉。本文即针对不可旋转与LIFO约束(Sequential and Orientated Loading, 2|SO|L)下的2L-CVRP展开研究。

2 ISA-LOS算法开发

2.1 基于最少开放剩余空间的LOS方法设计

求解2L-CVRP的关键是装箱方法，而LIFO约束是指每个货物在不移动其他货物的情况下可以直接卸载。针对LIFO约束的装箱问题，本文提出了基于LOS的矩形放置方法。首先定义开放矩形空间(Open Space, OS)，OS指与容器开放边缘相交的矩形区域。如图2所示，M1、M2、M3、M4、M5的上边缘与容器开口相交，放入其中的货物能够直接卸载，即为OS,M6中的货物不能直接卸载，故不是OS。与M6原理类似，W1是放入R1后所产生的浪费空间。

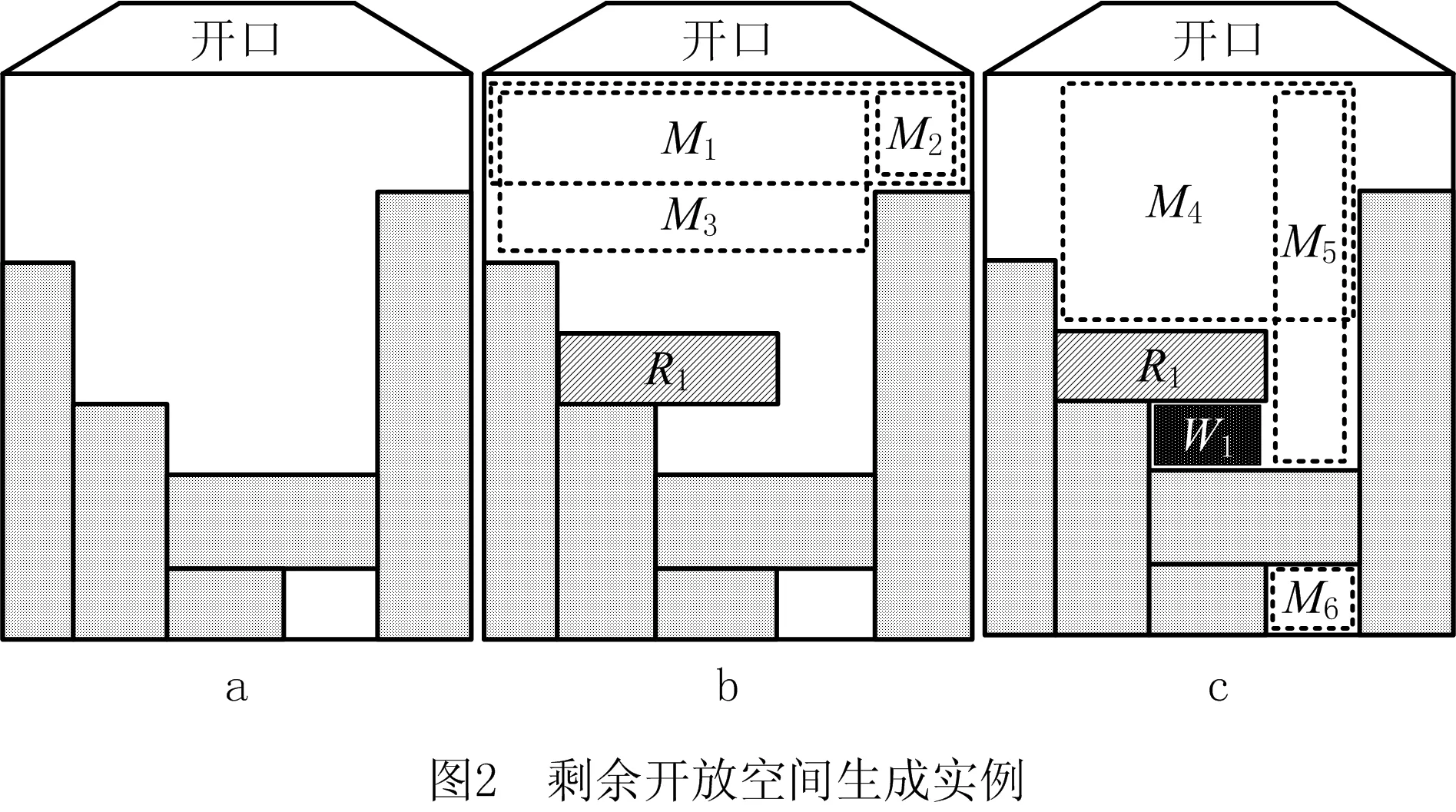
对于货物位置选择，LOS装箱方法遵循以下步骤与原则：①选择当前矩形的所有可放置位置；②计算每个位置放置后所产生的OS数量；③基于OS数与其空间格局，构造适应度；④选取适应度最小的放置状态为其当前位置。其中，具有┌形状的空间格局，需要向左延伸生成一个额外的OS，如图2中的M1所示；具有┐形状的空间格局，需要向右延伸生成一个较大的OS，如图2中的M4所示。对于放置后所产生的每个浪费空间，都给予k倍的适应度因子惩罚。

表1 不同惩罚因子下的图例适应度取值

装箱方法设计通常止于评价规则提出，鲜有高效的OS生成策略报道。实际上，剩余空间生成是装箱方法实现的关键，对其运行效率提升具有重要作用。为实现高效的LOS方法执行，本文给出了基于skyline的OS生成策略，如图4所示。具体操作流程与简要代码如下：

(1)根据容器格局，产生已放入矩形的不相交上边缘线，如图4b中的加黑线段所示。其中，每条上边缘线用其左角点x1坐标、右角点x2坐标与其y坐标表示。将所有线段按其y坐标由大到小排序，形成向量集合S*如式(1)所示:

(1)

(2)去除非开放空间的上边缘线，即去除如图4b中的线段S5。通过对集合S*第n行向量与第n行以下向量的左右角点x坐标比较，删除完全位于第n行线段以下的上边缘线。其操作策略如伪代码1所示。

伪代码1

将S*序列按y坐标由大到小排序

For i=1:n-1

Ind=find(S*((i+1):end,1)≥S*(i,1))&S*((i+1):end,2)≤S*(i,2))

If～isempty(ind)

S*(ind,:)=[];

End

End

(3)改变包含浪费区域的上边缘线，即改变如图4c中的线段S4。同样是基于S*中的行向量x坐标比较，其操作如伪代码2所示。

伪代码2

将S*序列按y坐标由大到小排序

For i=1:n-1

Ind2=find(S*((i+1):end,1)≥S*(i,1))&S*((i+1):end,1)≤S*(i,2))

If～isempty(ind2)

S*(ind2,1)=S*(i,2);

End

End

(4)通过前3步可生成当前空间的skyline集合S，即S=S*。针对空间中的┌角点，将引入新的skyline构造OS。在此，将S中的行向量按照x1坐标由小到大排列，如果存在yn>yn-1，则搜索第n行之前y坐标大于yn的行位置，例如[…;xp1,xp2,yp;…;xq1,xq2,yq;…;xn1,xn2,yn;…]中的p行和q行，取其中行数最大的向量[xq1,xq2,yq]为基准，生成skyline为[xq2,xn2,yn]。如此，通过┌角点搜索，将其向左延伸至已放置矩形，即可生成参考线。如图4d所示，由S1左角点向左延伸的新skyline为S5。其操作如伪代码3所示。

伪代码3

将S序列按x1坐标由小到大排序

For i=2:n

If S(i,3)>S(i-1,3)

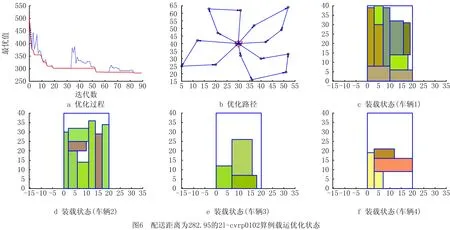
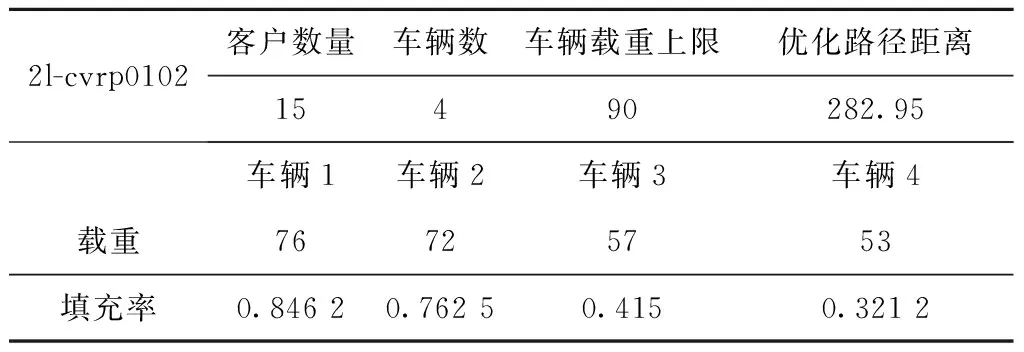
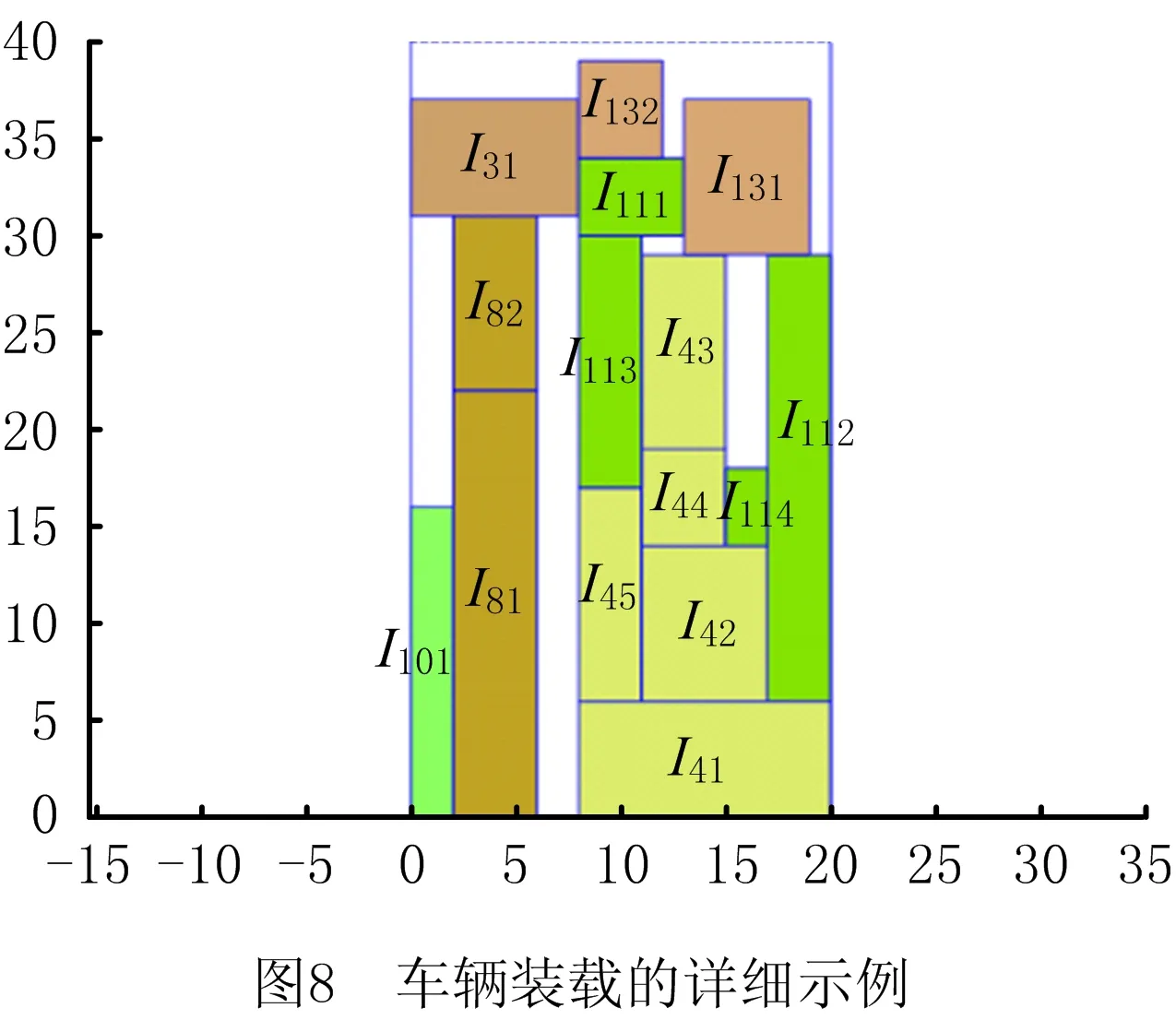
Ind3=find(S(i,3)

Ifisempty(ind3)

Sadd=[0,S(i,2),S(i,3)];

Else

Sadd=[S(max(ind3),1),S(i,2),S(i,3)];

End

S=[S;Sadd];

End

End

(5)由每条skyline的左角点位置向右上方延伸即生成OS，而相应的适应度(OS数)则可由集合S的行向量数表示。同时，所构建的skyline集合能够表示剩余空间格局，参与矩形放置迭代，支撑装箱方法执行。这是一种基于矩阵变换的简便适应度求解与装箱操作策略。

本文通过对容器格局的开放剩余空间构建，以OS数为基础生成适应度，适应度越小则表明该位置的放置效果越好，以此迭代选优完成装箱验证。LOS装箱方法继承了文献[11]中的剩余空间评价思想，不同的是，MOS方法[11]以当前矩形与其所在、与其干涉的OS空间为基础，进行新的OS生成与判定，该过程需要不断地对已有OS空间进行搜索和重组，不易于执行操作。LOS装箱方法则通过Skyline提取与处理，引入特定情况的新skyline生成和浪费空间惩罚参数，精简了适应度运算过程。同时，本文给出了基于矩阵变换的高效LOS装箱方法执行策略，弥补了具体的装箱操作缺失，提高算法运行效率。

2.2 带有回火操作的模拟退火算法构建

由于载重约束与装载约束的双重制约，致使2L-CVRP难于跳出局部较优解，优化性能受限。为此，本文参照文献[20]的模拟退火框架与操作，将LOS装箱方法与带有回火过程的模拟退火算法相结合，完成路径优化。具体流程如图5所示，灰色区域(1)即为回火操作，当退火温度T到达终止温度Tb时，升高退火温度T至T0。其中，每次回火温度T0逐渐下降，直至到达回火终止温度Tt为止，算法结束。回火操作通过周期性的退火温度上升，保持最优解继承与较优解跃迁的能力平衡，增加算法全局搜索能力。

图5中的灰色区域(2)为基于LOS方法的装箱模块，其目的是验证客户配送序列的可行性。首先，在给定序列中，分别对不同客户的货物面积、长度和宽度进行排序，构建三组初始解。之后，通过客户序列下的货物2-opt本地搜索寻优，形成装载序列，并进行逐个车辆的LOS装箱方法验证。当全部车辆的装载状态满足要求时，验证通过，否则重新邻域变换产生新解，依此循环。

为加速算法运行，将采取以下措施：

(1)采用“先评价，后装载”(evaluating first-packing second)策略[21]，即通过定量的预约束参数比较，减少装箱模块调用次数。只有当全部车辆的载重与填充面积不超过上限时，才调用装箱方法进行验证。

(2)记录已验证的成功与不成功配送客户序列，形成禁忌表Tbs与Tbf。为确保每次迭代产生可行新解Sn，降低禁忌表扩充对搜索效果影响，将中间解Sn*的生成次数设置为Min(n∧2,10 000)+size(Tbs,1)+size(Tbf,1)，n为总的配送客户数量。货物装载序列的随机变换次数为round((m∧4)×10×fr)，m为待装载货物数，fr为指待装载货物与容器的面积比，面积比越高则需要变换验证的上限次数越多。

(3)在中间解、预评价与装箱过程中，逐个检验车辆，一旦不符合要求直接跳出。在配送客户序列与货物装载序列生成中，一旦满足要求即退出搜索。

3 实验与分析

为验证ISA-LOS算法针对2|SO|约束下的2L-CVRP求解性能，将其运算参数分别设置为：初始温度T0=20、终止温度Tf=0.1、退火温度衰减系数a=0.85、马尔科夫链长度为n∧1.5(n为客户数)、回火温度衰减系数b=0.6、回火终止温度Tt=5、最大运算时间为3 600 s。使用MATLAB软件进行算法编程，并测试于CPU主频为2.8 GHz的电脑主机，取10次运算的最优值为计算结果。基于文献[4]所构建的国际经典数据集(其中包含36组算例)，本文提取数据集的前5组算例进行对比实验。由于每组的第一个算例为pure-CVRP问题，不予考虑，其运算结果如表2所示。

表2 2|SO|L约束下的部分2l-cvrp算例求解结果

表2中BKS为已知文献的算例最优解[11]，Imp=100×(BKS-cost)/BKS表示历史最优解与当前解的差距。如表2所示，ISA-LOS算法于20个算例中找到了6个算例的最优解，与BKS的平均差距为2.69%。实际上，在退火搜索中的初始解生成、邻域结构变换、更优解接受以及装载序列的2-opt变换中，均存在概率性的随机因素，因而影响算法结果。鉴于实验算例的10次计算结果选优，虽然没有找到全部历史最优解，但是2.69%的平均优化差距仍能表明ISA-LOS算法的可行性与有效性。

为进一步验证算法性能，将算例通过车辆数n=n+1或者n=n-1的方式进行最优路径求解。表3给出了相应的车辆数与运输距离，其中加黑数据为不大于BKS的计算结果，加*数据为优于BKS结果。如表3所示，ISA-LOS取得了6个算例的更优解，7个算例的BKS解，与历史最优结果的平均差距为0.59。基于车辆载运条件更改，ISA-LOS能够实现更为优异的计算结果获得，验证了所提出方法的求解性能。

表3 2|SO|L约束下的部分2l-cvrp算例最优路径距离

优于BKS的2l-cvrp0102迭代过程与载运效果如图6所示，具体车辆的载重与填充率分配如表4所示；等同于BKS的2l-cvrp0505迭代过程与载运效果如图7所示，具体车辆的载重与填充率分配如表5所示。对于图7a中的路径寻优过程，每次回火操作都扩大算法对非更优解的接受概率，平衡载重、装载双重约束下的优解继承与非更优解接受，推动算法全局寻优。对于车辆装载约束，一旦满足装箱条件则自动终止算法运行，因此图7中的装载效果并非最优布局。实际上，为加速算法运行，无需实现车辆装载的完全优化。

表4 配送距离为282.95的2l-cvrp0102算例载运参数

图7c中的空间装载状态表示如图8所示，车辆1的客户服务顺序(路径顺序)为I13、I11、I4、I3、I8、I10，每个客户所需货物用相同颜色表示(具体货物参数可查阅文献[4])。考虑LIFO约束，将货物的填装顺序按照I10、I8、I3、I4、I11、I13排列，具体客户内的货物顺序由2-opt算法确定。由图8可知，LOS装箱方法在最左下角的放置规则下，通过最少剩余空间评价，使容器格局保持了尽可能的平滑与完整，有利于后续货物放入。同时，货物装载没有旋转，且每个客户的所需货物卸载都不需要移动其他货物，满足2|SO|L约束。

表5 配送距离为375.28的2l-cvrp0505算例载运参数

4 结束语

为求解2L-CVRP，通常需要从以下3方面展开研究：①开发具有强全局搜索能力的启发式算法，用以解决载重、装载双重约束下的精准路径寻优；②设计符合配送约束的装箱方法与其执行策略，满足迭代操作的反复快速调用；③加速整体算法的优化构建与运算，实现多模块嵌套的高效问题求解。本文针对LIFO约束下的2L-CVRP，首先提出了基于最少剩余空间的LOS装箱方法。该方法通过剩余空间数量检测，结合相应的容器格局修正系数，完成了针对放置位置的适应度构造，从而指导给定序列的货物装载效果验证。同时，详细给出了基于skyline的简便剩余空间生成策略，优化装箱模块运算。之后借鉴文献[20]中带有回火过程的模拟退火操作，融合LOS装箱模块，构建了ISA-LOS算法。为提高算法的运行效率，分别设计了不同模块的算法加速结构与参数设置方程。

本文针对国际标准数据集进行运算，并将实验数据与已知文献的最优结果进行对比。结果表明，在有限的计算次数下，ISA-LOS算法能够取得不错的解。基于可变车辆数的配送路径规划，算法获得了20个算例中6个更优解，7个等BKS解，且与已知文献的最优解差距很小。基于求解效果分析，回火过程能够促使迭代跳出局部较优解，增强算法寻优性能。装箱模块实现了LIFO约束下的货物合理填装，证明了ISA与LOS方法的可行性与有效性。

受限于具体的算法编程与实现方法，本文仅对标准数据库中的前5组算例进行了对比实验。进一步，一方面将提高算法运行效率，实现更大规模的算例求解；另一方面，将扩展ISA与LOS方法至其他2L-CVRP与3L-CVRP，完善相关问题优化。