增材制造自适应螺旋加工路径规划方法

郑 冉，刘芝平,2，易 兵+，杨 岳

(1.中南大学 交通运输工程学院，湖南 长沙 410075；2.长沙理工大学 汽车与机械工程学院，湖南 长沙 410004)

0 引言

增材制造技术具有可加工复杂几何结构、材料利用率高、生产成本低和研发周期短等诸多优势，被广泛运用于航空航天、汽车、船舶、涡轮叶片以及传统机械等领域。增材制造技术的出现推动了产品生产向个性化、定制化发展，实现了产品制造工艺、制造技术以及制造方式的重大变革[1-2]。随着增材制造技术的广泛运用和相关研究的不断深入，提升增材制造的效率和产品质量成为当前研究的热点，主要包括研究新的打印方式和研究新的打印材料两方面。增材制造加工路径是影响加工效率和产品质量的重要因素，尤其是对于新打印材料增材制造。加工路径的长度和连续性决定了零件的加工效率，而加工路径的光顺性及相邻路径间距均匀性又直接关系到零件加工质量。因此,增材制造路径规划对提高加工效率和质量具有重要意义，尤其是碳纤维复合材料增材制造过程[3-4]。

增材制造主要采用自带切片软件产生的加工路径，然而现有方法生成的加工路径具有尖角过多、均匀性差，甚至出现路径自相交等问题。之字形路径[5-6]是增材制造最传统的加工路径，也是最简单的路径。但之字形路径存在尖角较多和路径光顺性差等问题，导致打印过程需要不断改变打印头运动方向，严重影响加工效率。同时，尖角部位打印头运动方向急转，容易出现过度填充或填充不足以及加工边界翘曲变形等问题，大大降低零件加工质量。轮廓偏置路径[7]与之字形路径相比，提高了加工路径平滑性，但路径不连续，喷头运动路径长度增加且加工效率降低，相邻路径之间切换时依然存在过度填充风险。Hilbert曲线填充方式[1]、三角形填充形式[8]和蜂窝形填充形式[9]虽然能够保证填充曲线遍历整个加工区域，打印件强度较高，但打印速度慢，且存在尖角过多的问题，从而降低零件加工质量。

螺旋加工路径能有效地避免上述问题，可以形成一条连续、平滑、没有尖角、没有交叉的加工路径，已经被运用到传统的铣削加工中。目前关于螺旋刀具路径生成方法的研究主要包括：求解椭圆偏微分方程法、恒定残余高度法、基于中轴线算法、放样方法和双螺旋法。BIETERMAN等[10]提出的求解椭圆偏微分方程(如拉普拉斯方程和泊松方程)的方法能够有效减少加工时间，但该方法路径在接近边界和尖角处，螺旋线会变得稀疏，而在加工区域内部螺旋线基本为圆形，导致相邻加工路径的重叠，整个路径的均匀性难以保证;LEE等[11]提出的恒定残余高度法，可以保持残余高度不变，最小化加工时间,但该方法大多都需要进行自相交类型判断，增加了工作时间，且容易出现尖角，难以用于实际加工;HELD等[12]提出了基于中轴线的算法，通过将变化的圆盘插入加工区域的中轴来形成螺旋线，该方法形成的螺旋线没有自相交，但路径间距均匀性难以保证;文献[13-15]提出基于放样的线性插值螺旋曲线生成方法，该方法得到的螺旋加工路径较为光滑且有效减少了加工路径长度，但在加工边界尖角处，路径间距较大，容易出现切割不足的问题;ZHOU等[16-17]提出了双螺旋线方法，ZHAO等[18]提出了费尔马双螺旋方法，这种双螺旋路径连续光滑且可以使加工的起点和终点位于工件的外边界，但也难以避免螺旋线的尖角问题，并且很难保证路径的均匀性。

由此可知，现有螺旋加工路径生成方法均存在路径不均匀问题，尤其是对偏移路径进行复杂处理生成螺旋线过程复杂，效率低下，难以保证实际加工质量。因此，本文在放样方法生成螺旋刀具路径前期研究基础上，进一步研究增材制造自适应螺旋曲线生成方法。首先采用基于放样方法生成螺旋曲线，然后在尖角处等曲率大的地方自适应增加B样条曲线控制点，调整加工路径在尖角部位光顺性，提高整条螺旋加工路径相邻螺旋线螺旋间距的均匀性，解决加工路径在尖角处填充不足的问题；然后对自适应螺旋曲线路径填充情况进行检查，对于填充不到的边角区域进行后处理，以此得到更为精准、更加均匀的螺旋加工路径，并将其应用于增材制造，尤其是碳纤维复合材料增材制造加工过程，可有效避免现有增材制造软件自定义路径的自相交问题，对提高打印件表面质量和效率具有重要意义。本论文提出的基于B样条曲线表示的自适应螺旋加工路径，可直接用于具有非均匀有理B样条(Non-Uniform Rational B-Splines, NURBS)插补功能的数控系统，该自适应螺旋路径是Cn(n≥1)连续的光滑曲线，能有效提高加工精度和速度。

1 自适应螺旋加工路径生成方法

1.1 自适应螺旋加工路径生成方法概述

以不含岛屿规则正六边形为例，采用基于放样方法对正六边形加工区域进行自适应螺旋加工路径规划。如图1所示，设置正六边形加工边界外接圆半径R=200 mm，螺旋线圈数m=4。自适应螺旋加工路径生成的主要过程如下：

(1)对加工区域进行均匀放样，得到一系列放样点和放样线(如图1)，对放样线进行线性插值得到螺旋折线(如图1c)，放样线与螺旋折线交点即为B样条曲线初始控制点(如图1d)。

(2)根据B样条曲线方程，由初始控制点求得B样条曲线型值点坐标，并对型值点处曲线进行曲率求解。

(3)根据螺旋曲线上型值点曲率变化，自适应在曲线曲率较大处增加B样条控制点(如图1e)。

(4)以插入后的控制点为自适应螺旋曲线控制点，进行二次非均匀B样条曲线拟合，得到自适应螺旋加工路径(如图1f)。

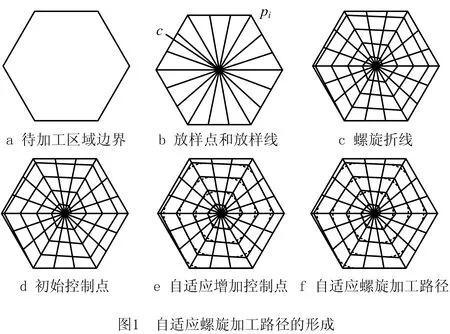
(5)根据自适应螺旋加工路径模拟结果检查待加工区域是否存在填充不足的问题，若存在该问题则在该区域重新规划自适应加工路径，再进行后处理，得到最终加工件。

1.2 放样生成螺旋路径初始控制点

首先对待加工区域边界进行均匀等分(如图1b)，将正六边形加工边界18等分，等分点为放样点pi(i=0,1,…,n)，选取正六边形中心点c为加工路径起点，中心点坐标根据放样点坐标计算得到:

(1)

放样点与中心点的连线为放样线，设最长放样线长度为lth，根据最长放样线与喷嘴直径求得待加工区域螺旋线圈数[13]:

(2)

式中：δ为喷嘴直径;[x]表示不小于x的最小整数。

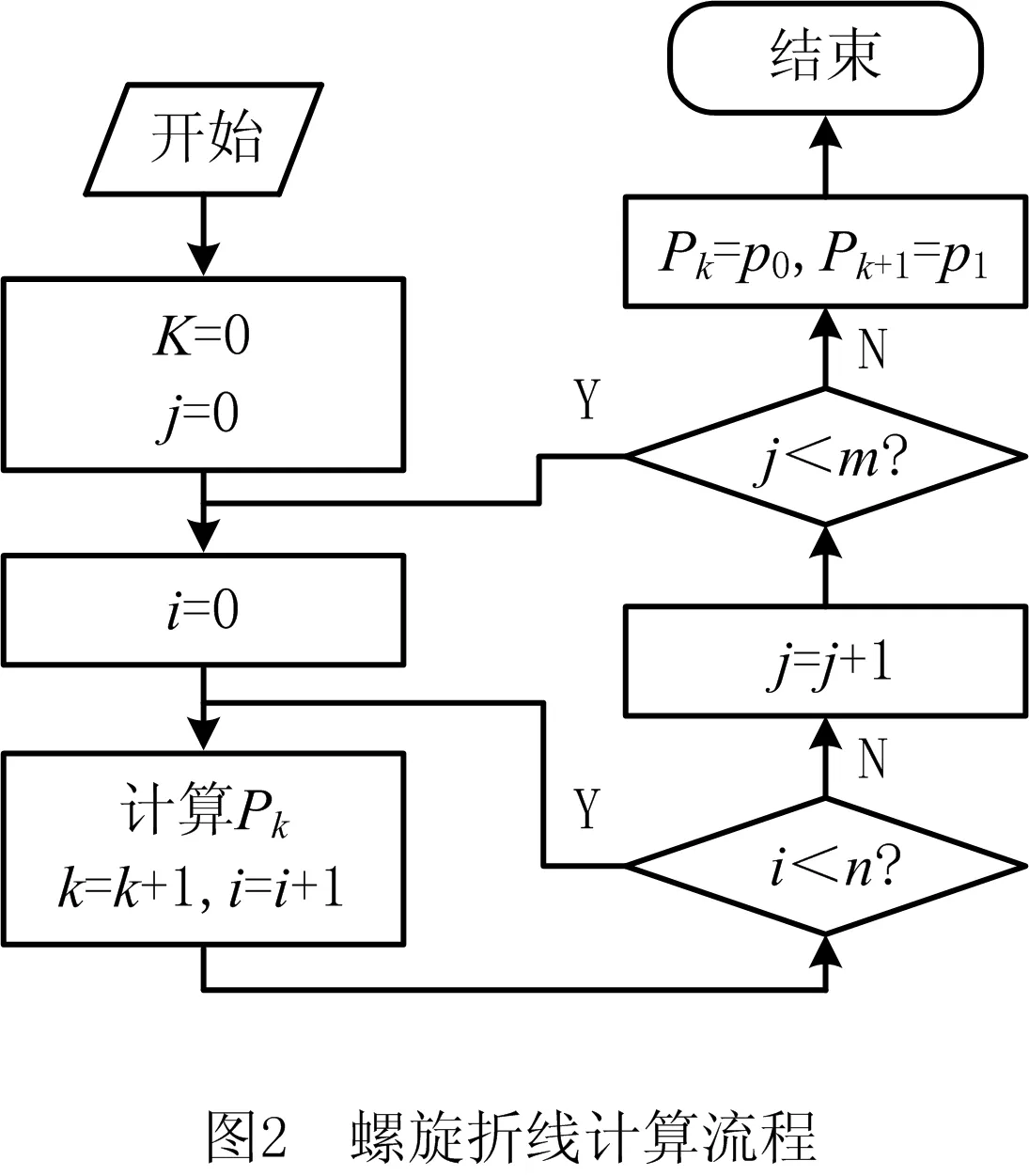
根据线性插值方法，按图2所示螺旋折线上点坐标求解流程求得螺旋曲线加工路径初始控制点P={Pk|k=0,1,…,K}，其中K=mn+1，连接各初始控制点得到螺旋折线[13]为：

(3)

1.3 B样条拟合螺旋加工路径

本文采用二次非均匀B样条曲线拟合螺旋加工路径，节点矢量U∈[0,1]是一个非递减的参数系列，U:u0≤u1≤…≤un+p+1，根据控制点数和B样条次数确定节点矢量的值[19]：

i=1,…,K-p-1。

(4)

式中：K为初始控制点数量;p为B样条曲线次数。当p=0时，B样条基函数为：

(5)

当p≠0时，B样条基函数为：

(6)

已知B样条曲线节点矢量和B样条基函数，根据定义求解p次B样条曲线型值点坐标：

(7)

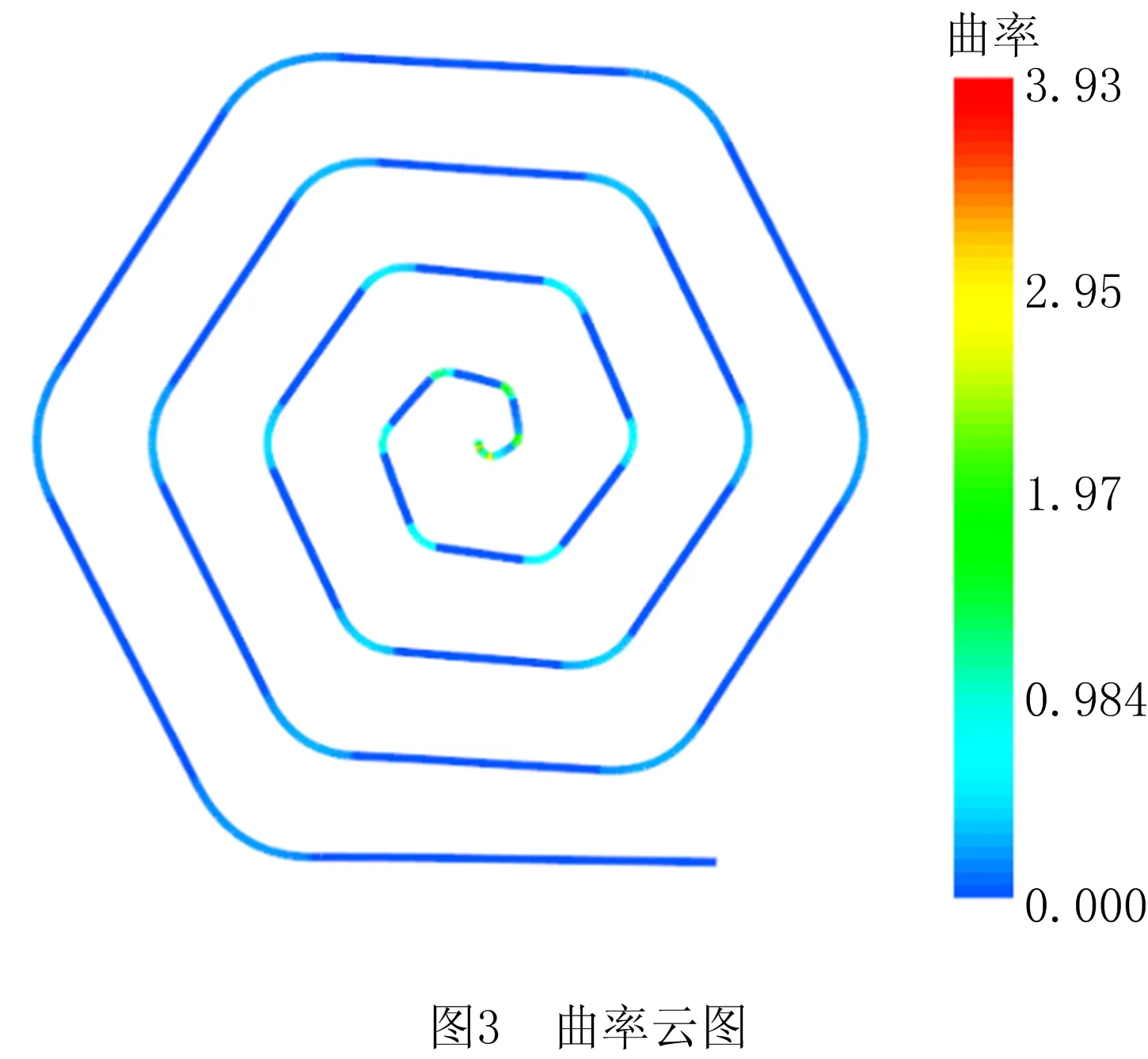
根据初始控制点坐标，用二次非均匀B样条拟合出正六边形螺旋加工路径，并对该路径曲率进行求解且云图显示，得到结果如图3所示，B样条曲线曲率求解公式为[20]：

(8)

1.4 自适应增加螺旋曲线控制点

由曲率云图3可知，基于放样方法形成的螺旋加工路径在正六边形尖角部分B样条曲线曲率较大，在直线部分曲率较小。由控制点连接形成的控制多边形是对B样条曲线的分段线性逼近，可以通过升阶或插入节点来改进这种逼近[19]。

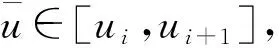
Qi=αiPi+(1-αi)Pi-1;

(9)

本文采用的节点插入算法步骤为：

(1)根据初始控制点拟合得到螺旋曲线，并求解其型值点曲率；

1.5 生成自适应螺旋加工路径

自适应插入螺旋曲线控制点后，得到自适应螺旋B样条曲线拟合的节点矢量u∈[0,1]、控制点坐标P={Pk|k=0,…,K1}(K1为插入后控制点数量)以及B样条基函数Ni,p(u)，根据最新数据求解二次非均匀B样条螺旋曲线上型值点坐标并进行曲线拟合[19]，即为自适应螺旋曲线加工路径(如图1f)。

(10)

1.6 自适应螺旋加工路径后处理

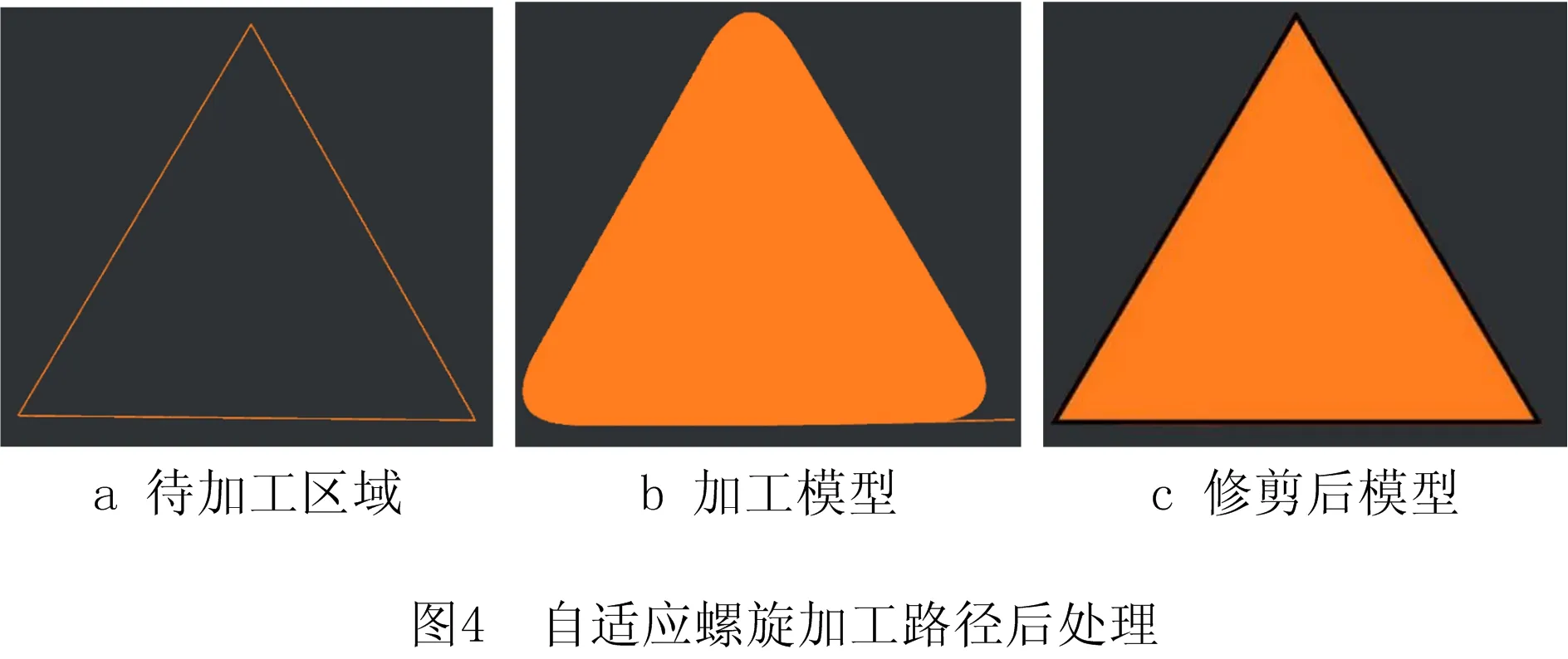
本文提出的自适应螺旋加工路径规划方法，在放样方法的基础上进一步研究，在尖角处增加控制点数，得到间距更加均匀、曲率更加光顺的螺旋加工路径。但自适应螺旋曲线路径在尖角部位为光滑的圆弧，若待加工区域面积较大，可能存在几何形状拟合不完全的情况，加工区域越大，这种情况越明显。因此，为避免边角填充不足问题，自适应螺旋加工路径拟合完成后需要检查待加工区域边角是否存在填充不到的问题，若存在该问题，则扩大实际加工区域面积，使之大于待加工区域面积，加工完成后进行边界修剪，得到最终加工模型，如图4所示。

2 实例验证

本文以Visual Stadio 2017为开发环境，以正方形、五角星、花朵3种加工边界为模拟加工实例，利用C++语言对基于放样方法和本论文自适应方法得到的螺旋加工路径进行模拟加工;以Visual Stadio 2008、VTK 5.10.1为环境进行螺旋曲线加工路径曲率云图可视化，笔者在前期研究工作中(参考文献[14-15])已经通过将放样方法生成螺旋加工路径应用于铣削加工，并通过加工实验证明了其有效性。因此，本文以正三角形、正五边形两种加工边界为例，基于放样和自适应两种方法分别对这两种加工边界进行螺旋路径规划，通过Visual Stadio 2017开发环境利用C++语言进行模拟加工得到螺旋曲线路径上型值点坐标，编写3D打印G代码，上传至3D打印切片软件ideaMaker进行三维路径可视化，以正五边形、五角星为例，在极光尔沃Z-603S 3D打印机上进行实际加工，验证该方法应用于增材制造的有效性。

2.1 模拟加工结果及对比分析

加工路径长度、连续性及光滑性等因素是影响加工效率和质量的重要参数，放样方法与轮廓偏置方法相比在形成螺旋加工路径长度、路径连续性、路径光滑性方面均得到了优化。本文在放样方法的基础上进行螺旋路径均匀性优化，自适应增加螺旋曲线控制点，得到更加均匀的螺旋加工路径，为证明本文自适应方法的优势，以加工边界正方形、五角星、花朵为例进行模拟加工和曲率求解，对放样方法与本文自适应方法形成的螺旋曲线距离均方根误差和方差值、曲线曲率均方根误差和方差值进行对比分析，如表1所示。模拟加工设置：正方形外接圆半径R=200 mm，螺旋曲线圈数m=10；五角星外接圆半径R=200 mm，螺旋曲线圈数m=8；花朵最大圈半径R=171.75 mm，螺旋曲线圈数m=5。基于放样方法得到的螺旋加工路径如图5a～图5c所示，3个模拟加工实例对应曲率云图如图6a～图6c所示。

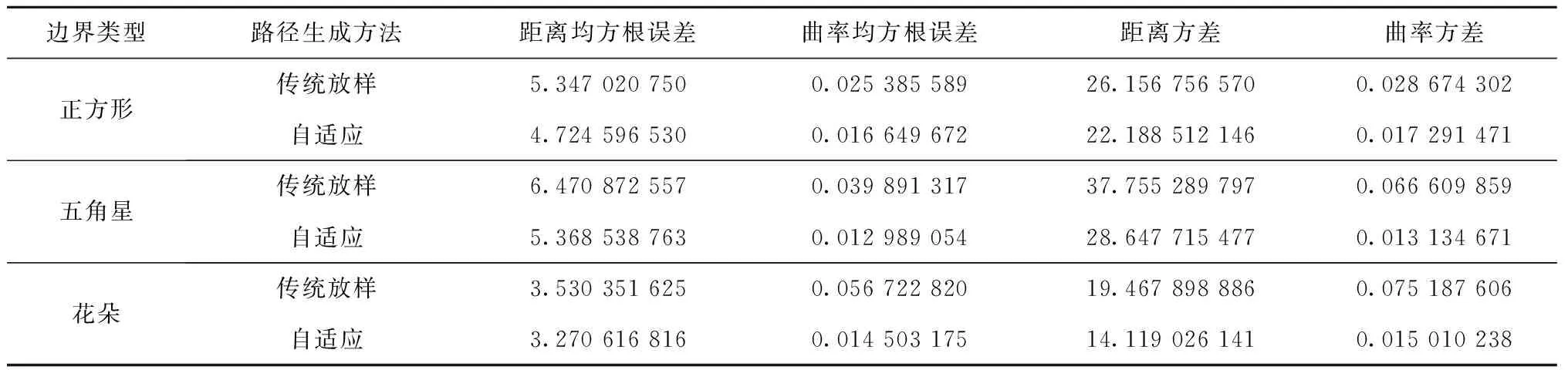
表1 不同路径生成方法距离和曲率的均方根误差、方差值对比

基于自适应方法得到的螺旋加工路径如图5d～图5f所示，3个模拟加工实例对应曲率云图如图6d～图6f。为便于观察，模拟加工实例曲率云图曲率值均扩大10倍。图5中红色点为B样条曲线控制点，黑色折线为螺旋折线，也是B样条曲线拟合的控制多边形，绿色点为螺旋样条曲线型值点，连接即为所求螺旋加工路径。

对比放样和自适应两种方法模拟加工正方形、五角星、花朵实例结果可知，放样方法得到的螺旋加工路径靠近起点部分螺旋线间距较为均匀，但随着螺旋路径不断向边界扩展，直线部位相邻螺旋线间距基本保持不变，尖角部位相邻螺旋线间距却越来越大(如图5a～图5c)。自适应方法形成的螺旋加工路径，在直线部分路径间距保持不变的同时，尖角部位相邻路径间距从加工中心到加工边界基本保持稳定，且与直线部分的路径间距差距极小，能够保证整个加工区域内螺旋加工路径的均匀性，避免增材制造过程填充不足或铣削加工铣削不到的问题，如图5d～图5f所示。对比表1两种方法生成的路径间距均方根误差和方差，可证明自适应方法间距优化的有效性。由表1中数据可知，自适应方法比放样方法生成的路径间距与喷嘴直径的距离均方根误差值更小，路径间距方差更小、更均匀。

对两种方法模拟加工例子的曲率云图进行对比可知，自适应方法形成的螺旋路径与放样方法形成的螺旋路径相比在间距更均匀的条件下，螺旋路径曲率值减小，路径更加平滑、光顺，如图6a～图6f。对比表1两种方法生成的路径曲率均方根误差和方差也可知，自适应方法生成的螺旋路径曲率均方根误差和方差两个参数值都比放样方法生成的路径值更小，从而说明自适应方法的路径光滑性效果更好。因此，自适应方法与放样方法相比能够得到间距更为均匀，曲线更为光顺的螺旋加工路径。

2.2 三维路径可视化及对比分析

设置三维路径可视化加工区域外接圆半径R=60 mm，喷头直径δ=0.4 mm，对正三角形、正五边形基于放样和自适应两种方法进行螺旋加工路径可视化的结果如图7所示。与之字形、轮廓偏置及Hibert曲线路径相比，放样方法生成的加工路径在路径长度和加工效率方面均有较大改进，本文以放样方法为研究基础，可以在保证路径长度较短、加工效率较高的前提下，得到曲线更光滑、更均匀的螺旋路径。路径不均匀是由于在实验加工过程中，喷嘴直径一定，尖角处螺旋线间距与喷嘴直径差值较大而导致。放样方法生成的螺旋路径在加工中心附近，路径均匀性可以基本保证，加工路径不存在填充不足的问题，但在靠近外边界部分可明显观察到相邻路径存在间隙，也就是未填充区域(如图7a和图7c)，对比两图可知放样方法生成的螺旋路径在尖角处越尖锐，路径光顺性越差，尖角处螺旋线间距与直线部分螺旋线间距差距越大，因此该方法生成螺旋曲线的不均匀性问题在路径尖角较为尖锐的加工区域更加突出。

由于插入控制节点前的控制顶点和插入节点后的控制顶点定义的是同一条B样条曲线，控制节点数量越多，控制多边形越接近所定义的B样条曲线[19]。本文提出的自适应方法，在螺旋路径尖角处B样条控制点数较多，控制顶点组成的控制多边形与B样条曲线所拟合的螺旋加工路径更加接近，可以在保证路径光滑性的同时，保证螺旋路径在整个加工区域内相邻曲线间距均匀，如图7c和图7d所示。对比放样方法与自适应方法的加工实例可知，自适应方法生成的螺旋加工路径在整个加工区域内不存在间隙，即在加工过程中不存在填充不足问题，且在路径尖角位置，与放样方法生成路径相比更加光顺。因此，本文方法生成的螺旋加工路径具有更好的加工质量和加工效率。

2.3 实例加工结果及对比分析

设置实际加工正五边形、五角星加工边界外接圆半径R=60 mm，喷头直径δ=0.4 mm，加工正五边形区域喷头温度为220 ℃，打印速度为70 mm/min，热床温度为60 ℃，层高0.2 mm，加工五角星区域喷头温度为215 ℃，打印速度为80 mm/min，热床温度为50 ℃，层高0.2 mm，打印材料选择直径为1.75 mm的PLA+，打印结果如图8所示。对比传统放样方法和本文自适应螺旋方法实际加工例子可知，传统放样方法生成的螺旋曲线尖角部位因相邻螺旋线的不均匀性导致了填充不足问题，且因曲线曲率变化较大，导致实际加工过程中喷头吐丝不畅，加工区域尖角附近出现了许多断丝现象，表面质量较差;本文提出的自适应螺旋曲线路径能够较好地解决带尖角特征加工边界内部材料填充不足问题，且能够改善因喷头运动方向在加工路径尖角部位急转使得加工过程中材料填充不连续进而导致表面加工质量较差的问题，从而验证了本文方法的可行性。

通过对比可知，本文提出的自适应螺旋加工路径能够对传统放样方法生成的螺旋路径尖角部位螺旋间距均匀性和曲线光顺性进行优化，且能够很好地应用于增材制造领域，尤其是碳纤维复合材料增材制造过程。

3 结束语

本文提出一种自适应螺旋加工路径生成方法，根据路径曲率变化自适应插入控制点，获得连续光滑B样条表达的螺旋曲线加工路径，既能减少加工时间，提高加工效率，同时也能够改善传统螺旋曲线加工路径间距的不均匀性，尤其是在尖角部位，避免铣削加工中欠切或增材制造材料填充不足的问题，大幅提高加工零件表面质量。

本文方法不仅能够用于传统高速铣削加工，还能够更好地运用于增材制造领域，能够根据切片廓形，自适应构建连续且不相交的新型螺旋加工路径，进一步提高增材制造加工效率和加工质量。最后通过模拟仿真实验和加工实例验证了本文方法的有效性，改善了传统螺旋曲线路径间距不均匀的问题，同时提高了螺旋曲线光顺性，达到了提高加工质量和加工效率的目标。

在增材制造过程中，打印材料具有方向性，容易造成加工件的各向异性，而本文提出的自适应螺旋加工路径只考虑单层填充形式规划而未考虑到层间交错填充问题，从而也难以解决层与层之间结合力下降的问题，因此下一步工作将研究三维自适应螺旋加工路径，减少打印工具的各向异性，提高层与层之间的相互作用。并且本文仅对机械加工中常见的凸多边形和简单凹多边形加工区域进行模拟和实际加工实验，对于复杂凹边界加工区域的加工路径规划方法和工艺参数优化方法将成为后续进一步的研究重点。