改进鲸鱼算法求解工程设计优化问题
2021-08-12刘景森马义想
刘景森,马义想,李 煜
(1.河南大学 软件学院,河南 开封 475004;2.河南大学 河南省智能数据处理工程研究中心,河南 开封 475004;3.河南大学 管理科学与工程研究所,河南 开封 475004)
0 引言
优化是一个非常活跃的研究领域,它在指定约束条件下探索给定问题的最优解,主要目的是解决一些复杂的大规模工程问题。目前优化领域最常用的有效方法之一是基于仿生学的生物元启发式优化算法,如受蚂蚁寻找食物过程中释放信息素发现路径行为启发提出的蚁群算法(Ant Colony Optimization, ACO)[1-3];受飞鸟集群捕食行为启发提出的粒子群算法(Particle Swarm Optimization, PSO)[4-6];受布谷鸟寄生育雏行为启发提出的布谷鸟搜索算法(Cuckoo Search Algorithm, CSA)[7-8];受蝙蝠利用声呐探测猎物、避开障碍物启发提出的蝙蝠算法(Bat Algorithm, BA)[9-11];受花朵授粉方式不同启发提出的花朵授粉算法(Flower Pollination Algorithm, FPA)[12-13];受樽海鞘在海洋中游弋和觅食行为启发提出的樽海鞘群算法(Salp Swarm Algorithm, SSA)[14-15];模拟蝴蝶觅食行为及散发香味特性提出的蝴蝶优化算法(Butterfly Optimization Algorithm, BOA)[16-17]等。这些机制各有特点、性能各具优势的算法,在不断地提出、改善、比较和优胜劣汰中,为解决大规模复杂实际工程优化问题提供了良好的解决思路与设计方案,也吸引了大量国内外学者的关注与研究。
函数极值优化问题是测试算法寻优性能的主要方法,而工程设计约束优化问题则是启发式优化算法的一个重要应用领域和研究热点。对工程设计问题的优化方法大致分为确定性抽象方法和元启发式方法两大类。确定性抽象方法对初始值敏感,是解决简单优化问题的一种有效方法,却通常无法解决复杂工程设计问题。而元启发式方法在求解复杂工程设计问题时有着独特优势,它使用目标函数与概率而不是确定性规则,有更多的机会找到更好的工程优化问题解决方案,如:ZHANG等[18]提出一种基于神经网络算法和教与学优化算法的有效混合方法;TSAI[19]提出一种改进的差分进化算法;DU等[20]提出了基于递减步长和逻辑混沌映射的果蝇优化算法;ZHANG等[21]提出一种基于布谷鸟搜索算法和差分进化算法的新型混合优化算法;DE MELO等[22]提出一种多视图差分进化算法;KUMAR等[23]提出一种改进的灰狼优化算法。这些改进算法均被应用于求解工程优化设计问题,并取得了较好效果,但其最优解质量和适用性都有进一步提升的空间。解决工程设计约束优化问题还需要探索寻优精度更高、普适性更强的算法。
鲸鱼优化算法(Whale Optimization Algorithm, WOA)是澳大利亚学者MIRJALILI等[24]受座头鲸特殊捕食行为启发提出的一种新型启发式搜索算法。该算法机制优越,寻优精度高,收敛速度快,且几乎不涉及参数设置,因此近年成为进化计算领域重要的研究和改进算法之一。如褚鼎立等[25]提出一种结合自适应权重和模拟退火的鲸鱼优化算法,提高了算法的寻优精度与收敛速度;CHEN等[26]提出了融入莱维飞行和混沌局部搜索的改进鲸鱼优化算法,并将其应用到工程设计问题;吴泽忠等[27]提出一种基于改进螺旋更新位置模型的鲸鱼优化算法,提高了算法的普遍适用性和稳定性;OLIVA等[28]提出一种基于混沌搜索的鲸鱼优化算法,提高了太阳能电池参数估计的准确性;肖子雅等[29]提出一种精英反向学习的黄金正弦鲸鱼优化算法,并通过仿真实验证明算法可以有效解决大规模问题,也可以应用于实际工程优化问题;WANG等[30]提出一种基于鲸鱼优化算法的新型混合系统,提高了风速预测的精度与准确性;黄清宝等[31]提出一种基于余弦控制因子和多项式变异的鲸鱼优化算法,提高了函数极值优化的寻优精度和稳定性;JIANG等[32]提出一种修改关键参数以实现分类搜索的鲸鱼优化算法,通过在CEC 2014函数的测试和3个约束工程问题的评估,证明了改进算法能够有效解决复杂、大规模、有约束的优化问题;ABDEL-BASSET等[33]针对置换流车间调度问题提出一种将鲸鱼优化算法与基于贪婪局部搜索策略结合的算法,提高了算法的性能。
虽然这些改进在相应领域提升了算法的寻优和应用能力,但鲸鱼优化算法的寻优稳定性、跳出局部极值的能力和对于工程设计约束优化应用的求解效果与适用性仍需得到更大程度的改进和提高。为了更好求解工程设计优化问题,提升鲸鱼优化算法的应用能力和寻优性能,本文提出一种基于分段式随机惯性权重和最优反馈机制的鲸鱼优化算法(Feedback Whale Optimization Algorithm, FWOA)。在随机游走觅食策略中引入基于当前全局最优解的反馈机制,在维系种群多样性的同时避免随机选择个体的盲目性,加快算法收敛速度,增强求解稳定性;在收缩包围策略和螺旋气泡网捕食策略中引入分段式随机惯性权重,调节算法全局勘测能力和局部开采能力的平衡,不仅加快了算法的收敛速度,也降低了后期因惯性权重单调递减直接陷入局部极值无法跳出的风险,有利于算法摆脱局部极值,找到全局最优值;对越界处理进行修正和改进,消除了已有进化成果可能丢失的隐患,解决了因较多个体越界导致越界处理后大量趋同,损害多样性的问题。本文通过理论分析证明了改进算法FWOA和基本鲸鱼算法WOA的时间复杂度相同,算法改进但并没有降低执行效率。通过对比6种算法在12个复杂基准测试函数上进行不同维度的函数极值优化实验,测试结果表明,该改进算法的寻优性能和求解稳定性明显优于其他5种代表性算法。而对焊接梁、拉伸弹簧和压力容器3个具有挑战性的工程设计约束优化问题的求解,其结果也充分显示了FWOA算法在处理不同类型工程优化设计问题上优越的求解效果和良好适用性。
1 基本鲸鱼优化算法
鲸鱼优化算法(WOA)将鲸鱼捕食猎物的行为分为随机游走觅食、收缩包围猎物和螺旋气泡网捕食3种不同的策略,其具体步骤如下:
步骤1初始化WOA算法各项参数:种群规模N,空间维度dim,迭代次数Max_iter,鲸鱼初始种群xi(i=1,2,…,n)和最优鲸鱼的位置与适应度初值。
步骤2进入迭代,先对整个种群集中进行边界条件处理,然后对种群中的每个个体分别进行进化处理,计算系数向量Α和C,并产生均匀分布决策随机数p。
Α=2×a×r-a;
(1)
C=2×r。
(2)
其中:a在整个迭代周期内随着迭代次数的增加从2下降到0;r为[0,1]上的随机向量。
步骤3当决策系数p<0.5且|Α|≥1时,当前鲸鱼在全局空间内进行随机游走觅食,勘测范围较广,此策略的数学模型为:
D=|C×Xrand-Χ(t)|;
(3)
Χ(t+1)=Xrand-Α×D。
(4)
其中:t为当前迭代次数;Xrand为当前种群中随机选择个体的位置向量;Χ(t)、Χ(t+1)分别为当前鲸鱼个体在第t、t+1代的位置。
步骤4当决策系数p<0.5且|Α|<1时,说明当前座头鲸找到了猎物,正在进行收缩包围,此时将当前全局最优鲸鱼位置当作目标猎物位置(或最靠近目标猎物的位置),鲸鱼以当前全局最优鲸鱼的位置为基础解进行位置更新,这一过程的数学模型如下:
D=|C×Xbest-Χ(t)|;
(5)
Χ(t+1)=Xbest-Α×D。
(6)
其中Xbest为当前全局最优鲸鱼个体的位置。
步骤5当决策系数p≥0.5时,表示鲸鱼正在进行螺旋气泡捕食。首先计算当前鲸鱼与当前最优位置鲸鱼之间的距离,然后在两者的位置之间建立一个螺旋方程,即鲸鱼以螺旋气泡网捕食猎物。模拟座头鲸螺旋捕食行为的数学模型如下:
D′=|Xbest-Χ(t)|;
(7)
Χ(t+1)=D′×ebl×cos(2×π×l)+Χbest。
(8)
其中:D′为当前位置鲸鱼到当前全局最优位置鲸鱼的距离;b为用于定义对数螺旋形状的常数;l为[-1,1]之间的均匀分布随机数。
步骤6判断是否符合结束条件,若符合则记录当前最优解及其目标值,否则转步骤2进行下一轮迭代。
2 基于分段式随机惯性权重和最优反馈机制的鲸鱼优化算法(FWOA)
2.1 基于最优解反馈机制的随机游走觅食
在鲸鱼优化算法的随机游走觅食策略中,随机选取种群中一头鲸鱼的位置作为基础解进行位置更新,这种完全随机性选择虽然可以维系种群的活跃性,但也增加了算法的不确定性,导致算法的稳定性较差,减缓了收敛速度。其实在随机游走觅食过程中,可以通过反馈机制,使得鲸鱼并不仅进行无目的游走,还与当前最优位置的鲸鱼进行信息交流,这种方式不仅可以保持种群的多样性,还可避免随机选择个体的盲目性,本文引入的反馈数学模型如下:
Χnew_rand=Χrand+rand×(Χrand-Χbest)。
(9)
其中:Χrand为随机选择的个体;Χbest为最优鲸鱼位置。
由式(9)可以看出,新鲸鱼的位置是由随机鲸鱼位置和最优鲸鱼位置共同决定的,在保证种群活跃性的同时加快了收敛速度。引入反馈机制后的鲸鱼随机游走公式为:
Χ(t+1)=Χnew_rand-Α×D。
(10)
2.2 分段式非线性递减惯性权重
动态惯性权重是平衡和调节算法全局勘测与局部开采能力的重要机制,较大的惯性权重意味着有较大的搜索步长,有利于算法进行全局搜索,增强跳出局部极值的能力,找到全局最优解;较小的惯性权重则是有利于算法进行局部开采,提高算法的收敛精度,加快收敛速度。而在鲸鱼优化算法的整个迭代期间,随着进化代数的增加,惯性权重的取值并没有发生改变,即采用较大的固定权重值,这虽然保证了算法的全局勘探能力,却不利于迭代后期鲸鱼向全局最优解附近进行精细搜索。
基于以上分析,本文将鲸鱼优化算法的收缩包围策略和螺旋捕食策略都分为前期、中期、后期3个进化阶段。在进化前期算法的惯性权重不变,即仍采用较大固定值,使算法在全局空间中进行充分搜索;而在中后期则引入非线性递减的动态惯性权重,使得鲸鱼向全局最优解附近靠近,加快算法收敛速度,引入的权重公式为:
(11)
式(11)中,惯性权重ω保持从1到0整体递减趋势的同时,也呈现出一定的随机性,这种随机性降低了算法如在中前期未能搜索到理论最优值附近,而在后期因惯性权重的单调递减直接陷入局部极值无法跳出的风险,有利于算法摆脱局部最优。加入惯性权重后,收缩包围策略与螺旋捕食策略的公式如下:
Χ(t+1)=ω×Χbest-Α×D;
(12)
Χ(t+1)=ω×Χbest+D×ebl×cos(2×π×l)。
(13)
2.3 修正且改进的边界处理
鲸鱼优化算法中的边界条件处理,是在每一轮迭代的开始处对上轮迭代形成的整个种群中所有个体集中进行各维度越界检查与处理,这种处理方式存在问题。因为在一轮迭代之中,对种群中每一个鲸鱼个体进行位置更新时,就应当考虑该个体的新位置是否越界,而不是在整个种群都已更新完毕后的下一轮迭代开始处,再集中进行边界条件处理。由于鲸鱼在游走觅食策略的位置更新时,就已经用到了本代种群中随机选择的鲸鱼,如果采取现有的越界处理方式,会导致选择的随机个体可能是位置越界的鲸鱼,从而造成连锁反应引起更多个体越界,而大量的越界和下轮迭代开始处的集中式越界处理会使种群中大量个体重新随机化,中断和破坏了已有的进化成果,降低了算法的收敛速度和求解精度,这也是WOA求解不太稳定的一个重要原因。因此,本文采取将边界条件处理放在每个个体位置更新后立即进行,并对边界处理方法进行了改进。在WOA中,如果某一维或若干维的位置超出设定边界范围时,都是将其设置为边界的最大值或最小值,这样虽然可以使鲸鱼的位置限定在合法区域内,但却降低了种群的活跃性,如果越界情况较多,处理后的结果将过于趋同,不利于算法找到最优解。本文算法在进行边界条件处理时,会选择在靠近相应边界的区域内随机产生一个数值代替越界值,如果在某个维度上低于该维度的边界下限,就产生一个靠近此下限的值代替其值,如果在某维度上大于此维度的边界上限,则产生一个接近该上限的值代替其值,代码如下:
for i=1:dim
for j=1:N
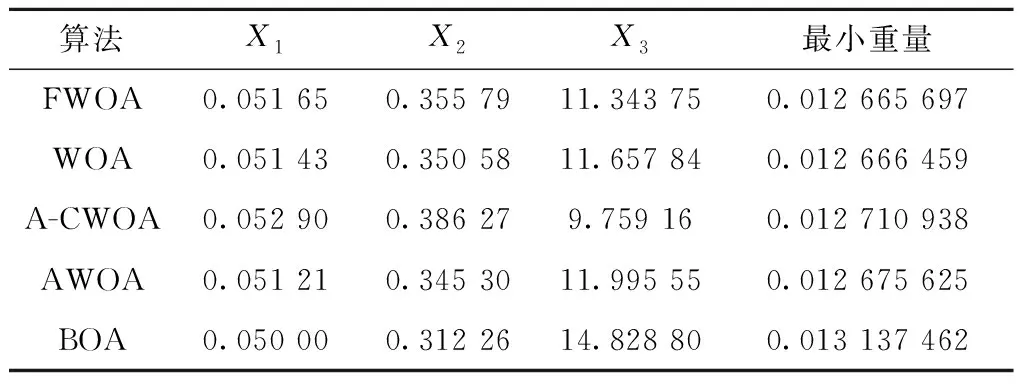
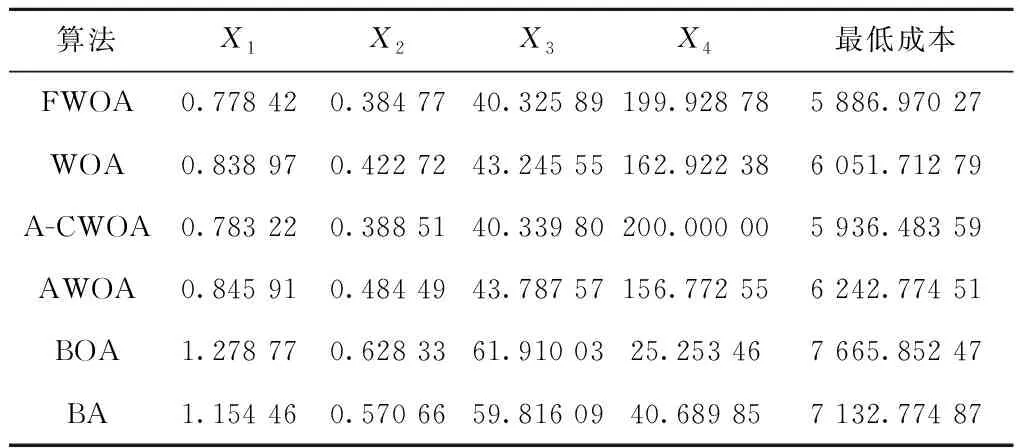
if(u(i,j) u(i,j)=unifrnd(0,0.05)*(Xmax-Xmin)+Xmin end if if(u(i,j)>Xmax) u(i,j)=unifrnd(0.95,1)*(Xmax-Xmin)+Xmin end if end end 由上述代码可以看出,改进公式不仅能增强种群的活跃性,还能提高算法的稳定性,符合改进规律,使边界处理更加合理和有效。 FWOA算法描述如下: 初始化鲸鱼种群xi(i=1,2,…,n) 设置最优鲸鱼位置与适应度的初值 while(t≤Max_iter) 由公式(11)计算非线性惯性权重ω for i=1:n 由公式(3)和(4)更新系数向量Α和C的值 if p<0.5 if|Α|≥1 由反馈公式(9)更新随机鲸鱼位置 以随机鲸鱼位置为基础解,依据公式(10)进行随机游走觅食 else 由式(12)以当前最优解为基础进行收缩包围猎物 end if else 由式(13)以当前最优解为基础进行螺旋捕食 end if 进行边界条件处理 计算新的适应度值,确定当前最优值和最优值位置 end for end while 输出结果 时间复杂度体现了算法的运行效率,是评判算法性能优劣的重要因素。在基本鲸鱼优化算法中,假设种群规模为N,个体位置的维度为n,设置最优鲸鱼的初始位置与适应度初值的时间为t1,初始化鲸鱼个体位置中每一维的时间为t2,则初始化阶段的时间复杂度为: T1=O(t1+N(n·t2))=O(n)。 进入迭代后,总迭代次数为Max_iter。假设对种群中每只鲸鱼每一维进行边界条件处理的时间为t3,计算目标函数适应度值的时间为f(n),与当前最优适应度值比较替换的时间为t4,系数向量Α和C的计算时间为t5,则该阶段的时间复杂度 T2=O(N(n·t3+f(n)+t4+t5)) =O(n+f(n))。 假设种群中有m1头鲸鱼进行随机游走觅食,m2头鲸鱼进行收缩包围猎物,m3头鲸鱼进行螺旋路径游走攻击猎物(N=m1+m2+m3,0≤m1,m2,m3≤N),鲸鱼个体在执行这3种不同策略时,每维位置更新的时间分别为t6、t7、t8,则该阶段的时间复杂度 T3=O(N(m1(n·t6)+m2(n·t7)+ m3(n·t8)))=O(n)。 综上所述,WOA总的时间复杂度 T=T1+Max_iter(T2+T3)=O(n+f(n))。 在FWOA算法中,种群规模为N,个体维度为n,均与基本鲸鱼优化算法一致。两者初始化过程一样,这一阶段的时间复杂度相同,均为T1=O(t1+N(n×t2))=O(n)。 进入迭代后,总迭代次数仍为Max_iter。假设:惯性权重w的计算时间为ξ1,系数向量Α和C的计算时间仍为t5,则该阶段的时间复杂度 (O(N(t5)))=O(ξ1+t5)。 假设鲸鱼个体每一维进行越界处理的时间为ξ6,计算目标函数适应度值的时间f(n)、与当前最优适应度值比较替换的时间t4都和基本WOA算法一致,则该阶段的时间复杂度 =O(n+f(n))。 由上可得,改进算法FWOA的总时间复杂度 基于上述分析可知,本文改进算法FWOA和基本鲸鱼优化算法WOA的时间复杂度相同,并没有降低算法的执行效率。 为了验证本文算法FWOA的整体性能,本文进行了两部分实验。4.1节将算法在12个复杂无约束基准测试函数上进行低、中、高3种不同维度的函数极值优化测试,用以验证算法的寻优性能与收敛能力。4.2节研究了3个具有挑战性的工程设计约束优化问题,用以检验算法在不同类型工程优化设计问题上的求解能力和应用潜力。两部分实验都将本文算法FWOA与基本鲸鱼优化算法(WOA)、A-CWOA(A-C parametric whale optimization algorithm)[34]、AWOA(adaptive whale optimization algorithm)[35]、蝙蝠算法(BA)、蝴蝶优化算法(BOA)共6种算法进行了对比。基于算法性能比较的公平性原则,6种对比算法采用相同的软、硬件平台,运行环境为Windows10操作系统、编程语言为MATLAB R2016a。仿真实验中,6种算法的运行次数、种群规模、空间维度和最大迭代次数都保持一致,即N=30,dim=10/50/100,N_iter=1 000,每种算法分别独立运行30次。 在算法参数设置方面,4个鲸鱼类算法中用于定义对数螺旋形状的常数b的值均设为1;蝴蝶优化算法中幂指数a的值为0.1,感知形态c的初值为c=0.01,转换概率p=0.8;蝙蝠算法的声波响度A0=0.25,脉冲发动速率r0=0.5。6个算法的参数设置采用的都是其各自基本算法的原有标准值,本文未另做挑选和更改,这进一步增强了实验结果与对比分析的客观性、公正性和可信性。 4.1.1 寻优精度分析 为了测试本文算法FWOA的求解性能,将其与上述5种对比算法在12个具有不同特征的基准测试函数上进行函数优化对比测试。具体测试函数如表1所示。 表1 测试函数 表1所列的12个基准测试函数中:F1(x)、F2(x)、F4(x)、F6(x)、F7(x)是单峰函数,全局搜索相对比较简单,大多数算法的优化结果都能达到理论最优值附近,主要用来测试算法的求解精度与收敛能力。F3(x)、F5(x)、F8(x)-F12(x)是多峰函数,这类函数大多具有多个极值点,用来检测算法能否摆脱局部极值找到全局最优解,其中:函数F5(x)的全局最优值周围有无数个极小值点,且全局最优值与这些极小值点之间存在极大值点,因此该函数具有强烈的震荡特性,很难找到全局最优值,非常考验算法跳出局部极值的能力;而函数F10(x)是F5(x)的一个升级版函数,不但具有F5(x)的所有特点,而且函数图像是层层叠加的,求解难度上升了很多倍;函数F11(x)是通过增加正弦函数频繁产生局部极小值,且极小值的位置分布不是对称的;函数F12(x)则是通过指数函数进行调节,含有大量的障碍物,且极值点个数随着空间维度的增加呈梯度增加,更能考验算法求解高维复杂函数的能力。这些各具特点的不同函数都有一定的求解难度,很适于测试算法的性能。 4.1.2 寻优精度分析 表2统计了6种对比算法在空间维度为10维、50维和100维的情况下,各自独立运行30次的最差解、最优解和平均值,并将各函数相应的最佳结果进行了加粗标注。 表2 6种算法在固定迭代次数下的寻优性能比较 续表2 观察表2的数据可知,在空间维度从10维增加到100维的过程中,FWOA、AWOA、A-CWOA、WOA和BOA 5种算法的寻优性能并没有出现太大程度的降低,这说明WOA和BOA有着较好的维度变化适应性,适于求解高维函数。而BA不但在寻优结果上不如这5种算法,而且维度变化适应性不佳,这也反映出最近几年一些新兴算法在寻优机制和能力上的进步。 观察6种算法在单峰函数上的寻优结果,可以看出各算法的整体开发能力。对于函数F1(x)和F7(x),FWOA和AWOA算法在不同维度下30次运行所找到的最差解、最优解和平均值都是理论最优值,其寻优性能远远超过A-CWOA、WOA、BOA和BA 4种算法。而对于函数F2(x)和F6(x),虽然AWOA算法找到的最优解非常接近于理论最优值,但仍稍逊于最差解、最优解和平均值都是理论最优值的FWOA算法。对于余下的单峰函数F4(x),这是12个函数中唯一使鲸鱼类算法随着维度增加寻优性能降低的函数,不仅WOA和A-CWOA表现不佳,就连寻优性能一向良好的AWOA表现也不尽人意,由表2中F4(x)的数据可知,AWOA算法在10维和50维下都找到了理论最优解,但仔细观察其在100维下的平均值和最差解可知,AWOA在这个函数上的表现并不稳定,而本文改进算法不但找到了全局理论最优,而且测试结果非常稳定,说明FWOA在单峰函数上的表现更好,高维适应性更强,算法的整体开发能力更优。而BOA虽然也受维度变化影响不大,但其整体的开发能力却略逊于鲸鱼类算法;仔细观察BA在这5个单峰函数上的表现可以发现,该算法在搜索区间较小的函数F2(x)和F4(x)上的寻优结果要远远优越于搜索区间较大的其余3个函数,这说明BA的局部搜索能力较好,而全局寻优能力相对较弱,算法进行大范围全面搜索时跳出局部最优的能力不足。 与单峰函数不同,多峰函数包含许多局部最优解,这些局部最优解的数量随着空间维度的增加呈指数增长,非常适于测试算法跳出局部极值的能力和对于维度变化的适应性。观察6种算法在多峰函数上的寻优结果,可以看到除了函数F11(x),FWOA和AWOA在不同维度下30次运行找到的最差解、最优解和平均值都是理论最优值,说明这两种算法具有很好的探测能力且跳出局部极值的能力较强。而A-CWOA、WOA、BOA和BA 4种算法在除F5(x)和F12(x)以外的多峰函数上找到的最差解、最优解和平均值都不是全局理论最优。与在单峰函数上表现类似,BA仍然在较大区间内搜索效果不太好,很容易陷入局部极值难以跳出。对于小搜索区间的多峰函数F5(x),4个鲸鱼类算法找到的最优解都是全局理论最优,而BA和BOA求得的最优解也很接近于此,但仔细观察在较大区间内搜索的多峰函数F3(x)、F9(x)、F10(x)、F12(x),BA找到的最优解不仅远远落后于WOA,与BOA相比,寻优结果也差了很多。 对于函数F11(x),6种算法虽都没找到全局理论最优值0,但FWOA在不同空间维度下找到的最差解、最优解和平均值都优于AWOA、A-CWOA、WOA、BOA和BA 5种算法,依然显示出更好的求解能力和维度适应性。 以上寻优精度结果表明,无论是单峰函数还是多峰函数,FWOA在各个维度下每次运行的结果几乎都是全局理论最优,表现出优越的求解性能。这些测试结果充分说明了FWOA较好地解决WOA在函数极值优化上寻优精度不高、容易陷入局部极值、寻优性能不稳定的问题。 4.1.3 收敛曲线分析 为了更直观地比较6种算法的寻优性能,各算法在迭代次数相同、维度为100情况下求解多峰函数F3(x)、F5(x)、F8(x)-F12(x)的收敛曲线如图1~图7所示。多峰函数能体现算法跳出局部极值的能力,更能说明算法的寻优能力,单峰函数的收敛曲线比较简单且结果与多峰函数类似,不再赘述。 从以上7个多峰函数图上可以看出算法的收敛速度和摆脱局部极值、寻找全局最优值的能力。FWOA在除了图2和图7以外的5个收敛曲线图上,收敛速度都是6种算法中最快的;虽在F5(x)和F12(x)上的收敛速度落后于AWOA和A-CWOA,但同样也找到了全局理论最优值,且观察表2中函数F12(x)数据可以发现,A-CWOA虽可以找到最优解,但并不稳定,而FWOA和AWOA算法找到的最优解、最差解和平均值都是全局理论最优,说明这两种算法不但跳出局部极值的能力较强,而且寻优过程中表现比较稳定。在图1和图3~图6中,A-CWOA、WOA、BOA三种算法的收敛曲线虽仍呈现下降趋势,但收敛速度比较缓慢,无法在1 000代内收敛到全局理论最优。BA更是从一开始便陷入了局部极值,收敛曲线几乎呈现水平状态,下降趋势极不明显,完全无法在1 000代内收敛到全局最优值附近。 由4.1.2节的寻优精度和图1~图7分析可知,在空间维度分别是10维、50维、100维的情况下,FWOA表现出非常优越的求解性能,在测试的12个基准函数各个维度上几乎都找到了理论最优值,且FWOA的收敛速度大部分明显比AWOA、A-CWOA、WOA、BA和BOA算法更快。这是因为FWOA算法在随机游走觅食策略中引入了基于当前全局最优解的反馈机制,不仅加快了算法的收敛速度,还增强了求解的稳定性;而在收缩包围策略和螺旋捕食策略中引入分段式随机惯性权重,可以在加快算法收敛速度的同时,降低算法在中前期如果未能搜索到理论最优值附近便会在后期因惯性权重的单调递减直接陷入局部极值无法跳出的风险,有利于算法摆脱局部最优,找到全局最优值。而对越界处理的修正和改进,不但消除了已有进化成果可能丢失的隐患,也解决了若种群中较多个体越界而在越界处理后过于趋同损失多样性的问题,有利于算法找到最优解,提高收敛速度与寻优精度。上述实验充分说明FWOA具有出色的寻优性能,其寻优精度、收敛速度、跳出局部极值的能力、维度变化适应性和求解稳定性均优于AWOA、A-CWOA、WOA、BA和BOA 5种对比算法。 为了验证本文算法FWOA求解工程约束优化问题的有效性,将FWOA和上述5种对比算法应用于焊接梁、拉伸弹簧和压力容器3个著名的标准工程优化设计问题。这3个工程问题具有各自不同的约束,本文采用通用的死刑惩罚函数机制处理这些约束条件,使算法在优化过程中自动丢弃不可行解。在求解这些工程优化问题时,每个算法均独立运行100次取其最佳寻优设计结果,参数设置也与4.1节相同。 4.2.1 求解焊接梁优化设计问题 焊接梁设计是一个著名的复杂约束工程设计问题,其目的是在剪应力、弯曲应力、屈曲载荷、端部挠度和侧面约束下找到最低制造成本。该问题有7个约束条件和4个设计变量,设计变量分别是焊缝厚度h(0.1≤h≤2)、焊缝长度l(0.1≤l≤10)、梁宽度t(0.1≤t≤10)、梁厚度b(0.1≤b≤2),具体数学模型如下: (1)设计变量: x=[x1x2x3x4]=[hltb]。 (2)目标函数: (3)约束函数: g1(x)=τ(x)-136 000≤0; g2(x)=σ(x)-30 000≤0; g3(x)=x1-x4≤0; (14.0+x2)-5.0≤0; g5(x)=0.125-x1≤0; g6(x)=δ(x)-0.25≤0; g7(x)=6 000-Pc(x)≤0; 表3统计了6种算法在求解焊接梁设计问题时得到的最佳解决方案数据,由表3可以看出,本文算法FWOA在h=1.820 0、l=2.688 28、t=9.035 30、b=0.205 80处得到的最小代价f(x)=1.591 25是找到的焊接梁设计问题的最低成本。这是因为本文算法引入的反馈机制和惯性权重提高了算法的局部搜索能力,基本鲸鱼算法是一个更擅于全局搜索的算法,特别是在大范围空间搜索时,算法比较稳定,这一点从4.1节的求解函数极值实验部分就可以看出。而焊接粱的设计变量取值范围比较小并受到多个约束条件的限制,需要算法有着较强的局部搜索能力,而本文改进则很好地满足了这一要求。 表3 6种算法求解焊接梁设计问题的最佳解决方案 4.2.2 求解拉伸弹簧优化设计问题 拉伸弹簧设计是一个最小化约束问题,其目的是设计一种重量最轻且满足挠度、剪切应力、波动频率、外径等4个约束条件和3个设计变量的拉伸弹簧。3个设计变量分别为线径d(0.05≤d≤2.00)、平均线圈直径D(0.25≤D≤1.30)、活性线圈数量N(2.00≤N≤15.00),该设计问题的数学模型如下: (1)设计变量: x=[x1x2x3]=[dDN]。 (2)目标函数: (3)约束函数: 表4所示为FWOA算法和其他5种算法求解拉伸弹簧设计问题的最小重量及对应设计变量的最优解。从该表数据可以看出,除了BOA和A-CWOA算法的求解结果相对较差外,其他几种算法求得的最终设计结果相差无几,且细微观察可以看出,FWOA求解出的弹簧重量是6种算法中最小的,说明本文算法对于求解这类工程设计问题具有良好的性能。 表4 6种算法求解拉伸弹簧设计问题的最佳解决方案 4.2.3 求解压力容器优化设计问题 压力容器设计问题的目标是使总成本最小化,包括材料成本、成型成本和焊接成本。该设计问题有4个约束条件和4个设计变量,设计变量分别是壳体厚度Ts(0≤Ts≤99)、封头厚度Th(0≤Th≤99)、壳体半径R(10≤R≤200)以及圆柱形截面长度Ls(10≤Ls≤200),其具体数学模型如下: (1)设计变量: x=[x1x2x3x4]=[TsThRLs]。 (2)目标函数: (3)约束函数: g1(x)=-x1+0.019 3x3≤0; g2(x)=-x2+0.009 54x3≤0; g4(x)=x4-240≤0。 表5统计了6种算法在求解压力容器问题时,得到的最佳解决方案的数据。可以看出,本文算法FWOA在Ts=0.778 84、Th=0.384 77、R=40.325 89、Ls=199.928 78处得到的最小代价f(x)=5 886.970 27不但是这几种算法求解压力容器设计问题的最低成本,而且其设计结果的成本远低于其他5种算法,充分说明FWOA在求解此类工程设计约束优化问题时具有优越的性能。 表5 6种算法求解压力容器设计问题的最佳解决方案 通过对以上3种不同复杂程度的著名工程约束优化问题的测试,充分说明了本文改进算法FWOA在处理不同类型工程优化设计问题上具有较好的应用潜力,不但能够提供很好的解决方案,而且求解结果也相当稳定。 为了更好求解工程设计约束优化问题,提升鲸鱼算法的寻优性能、求解稳定性和应用能力,本文提出一种基于分段式随机惯性权重和最优反馈机制的改进鲸鱼算法。在随机游走觅食策略中引入基于当前全局最优解的反馈机制,在维系种群多样性的同时避免了随机选择个体的盲目性,不仅加快了收敛速度,还改善了算法的稳定性。在收缩包围策略和螺旋气泡网捕食策略中引入分段式随机惯性权重,调节算法全局勘测能力和局部开采能力的平衡,不仅加快了算法的收敛速度,还降低了后期因惯性权重单调递减直接陷入局部极值无法跳出的风险,有利于算法摆脱局部极值,找到全局最优值。而对于越界处理的修正和改进,则消除了已有进化成果可能丢失的隐患,解决了当种群中较多个体越界而在越界处理后过于趋同造成多样性丧失的问题,提高了算法的寻优精度与收敛速度。通过理论分析证明了本文算法FWOA和基本鲸鱼算法(WOA)的时间复杂度相同,算法改进并没有降低执行效率。通过对6种算法在12个复杂基准测试函数上进行的不同维度函数极值优化仿真测试,结果表明,FWOA的寻优性能和求解稳定性都明显优于其他5种对比算法。而对焊接梁、拉伸弹簧和压力容器3个具有挑战性的工程设计约束优化问题的求解结果,也充分证明了FWOA在处理不同类型工程优化设计问题上具有很好的适用性和优越的求解效果。下一步将继续改进鲸鱼优化算法的寻优机制,不断提高求解性能,并进一步提升算法的应用能力和适用性,将其应用于更多领域问题的求解中。2.4 FWOA算法流程
3 时间复杂度分析
4 仿真实验
4.1 函数极值优化仿真实验

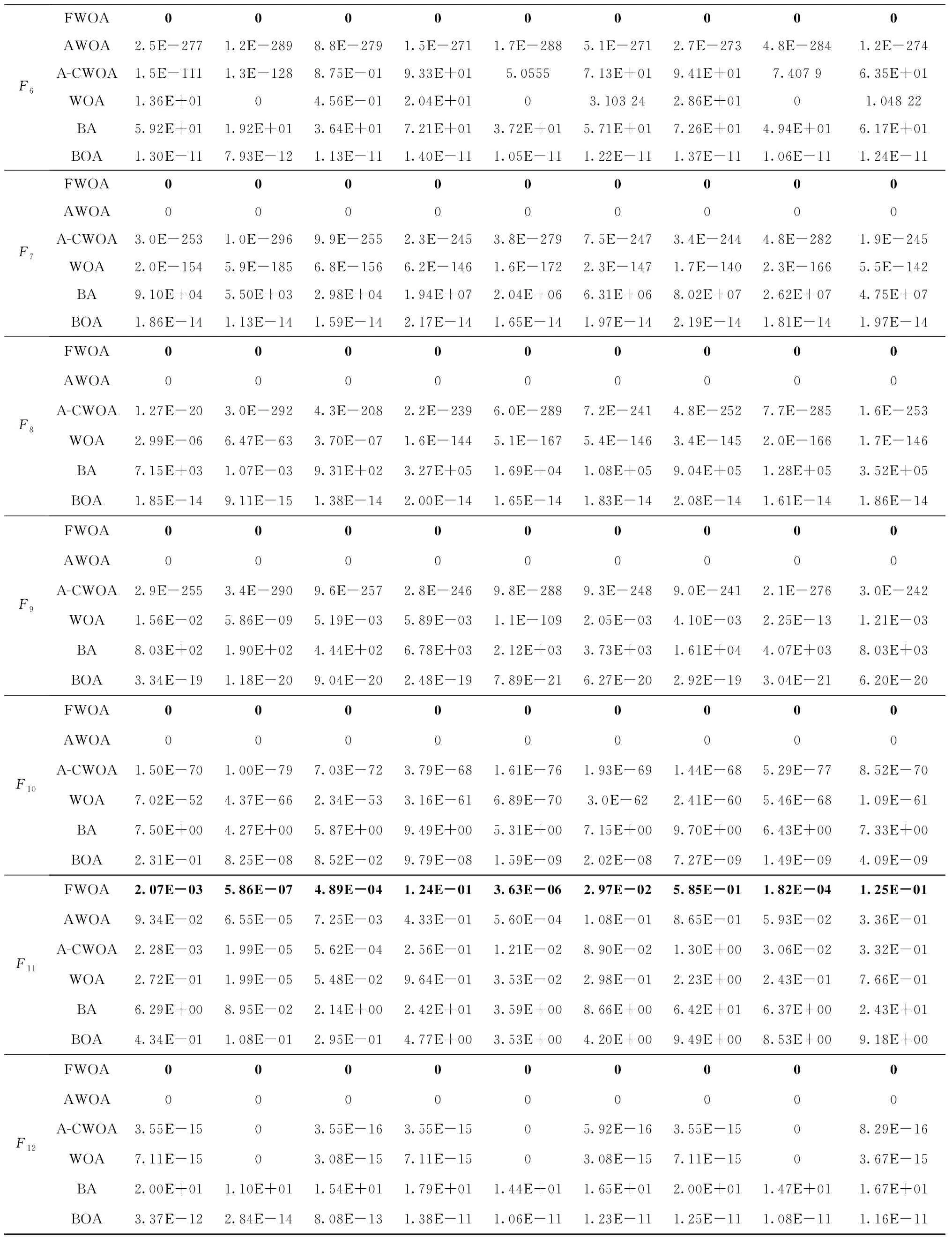
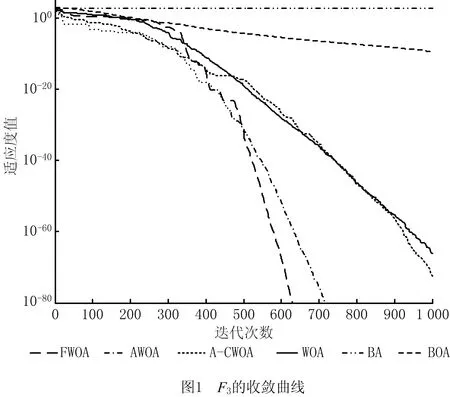

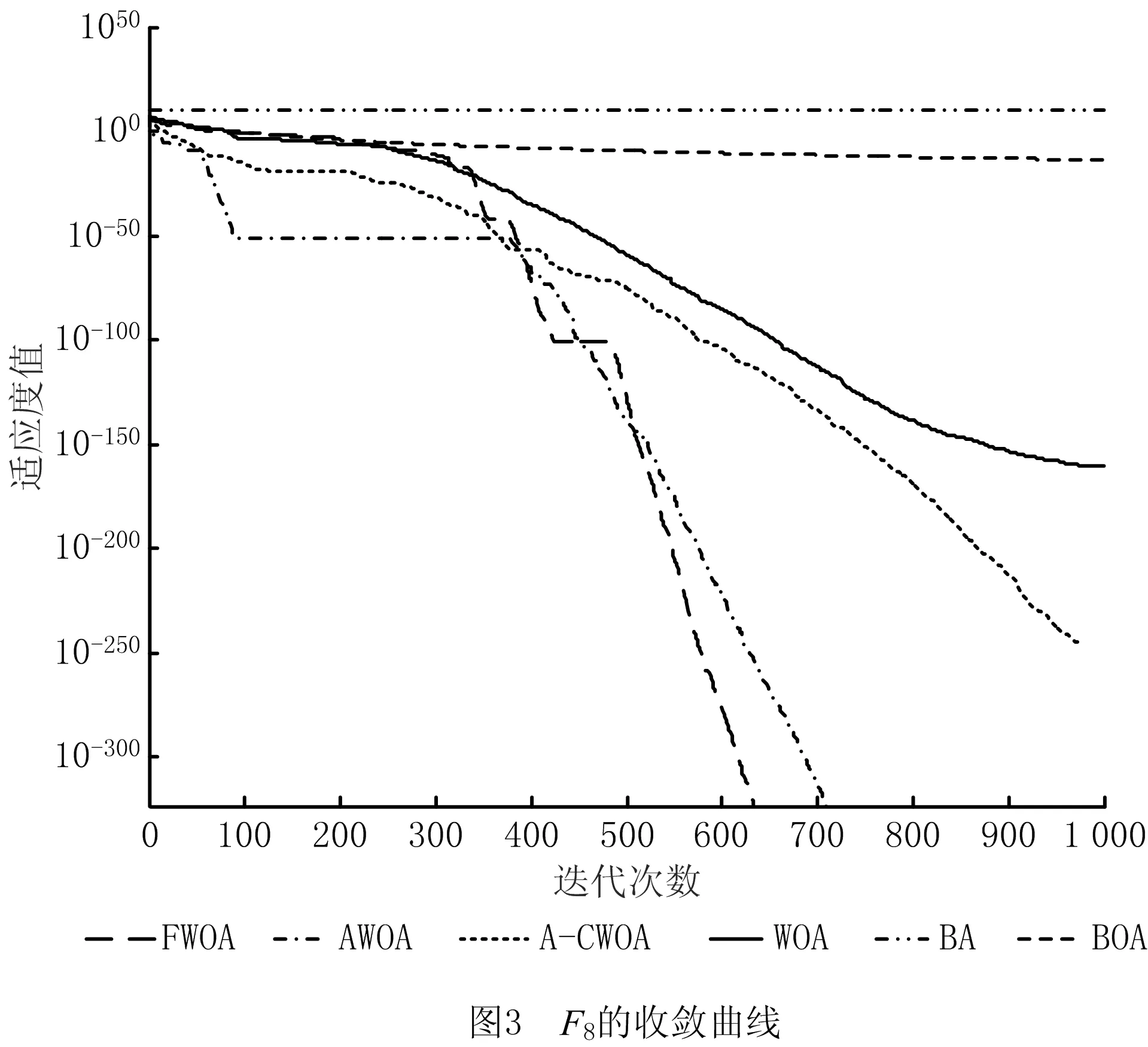
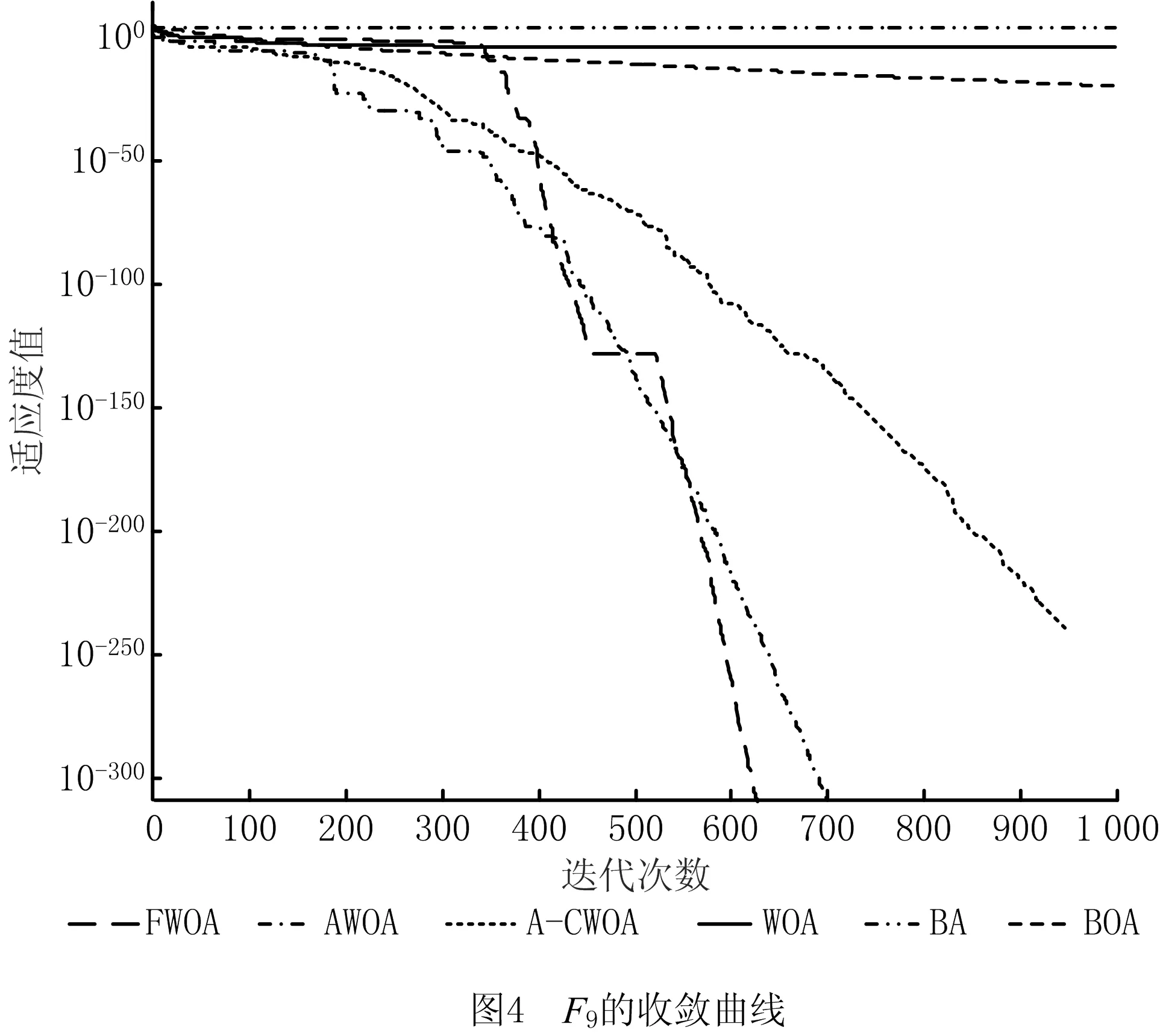
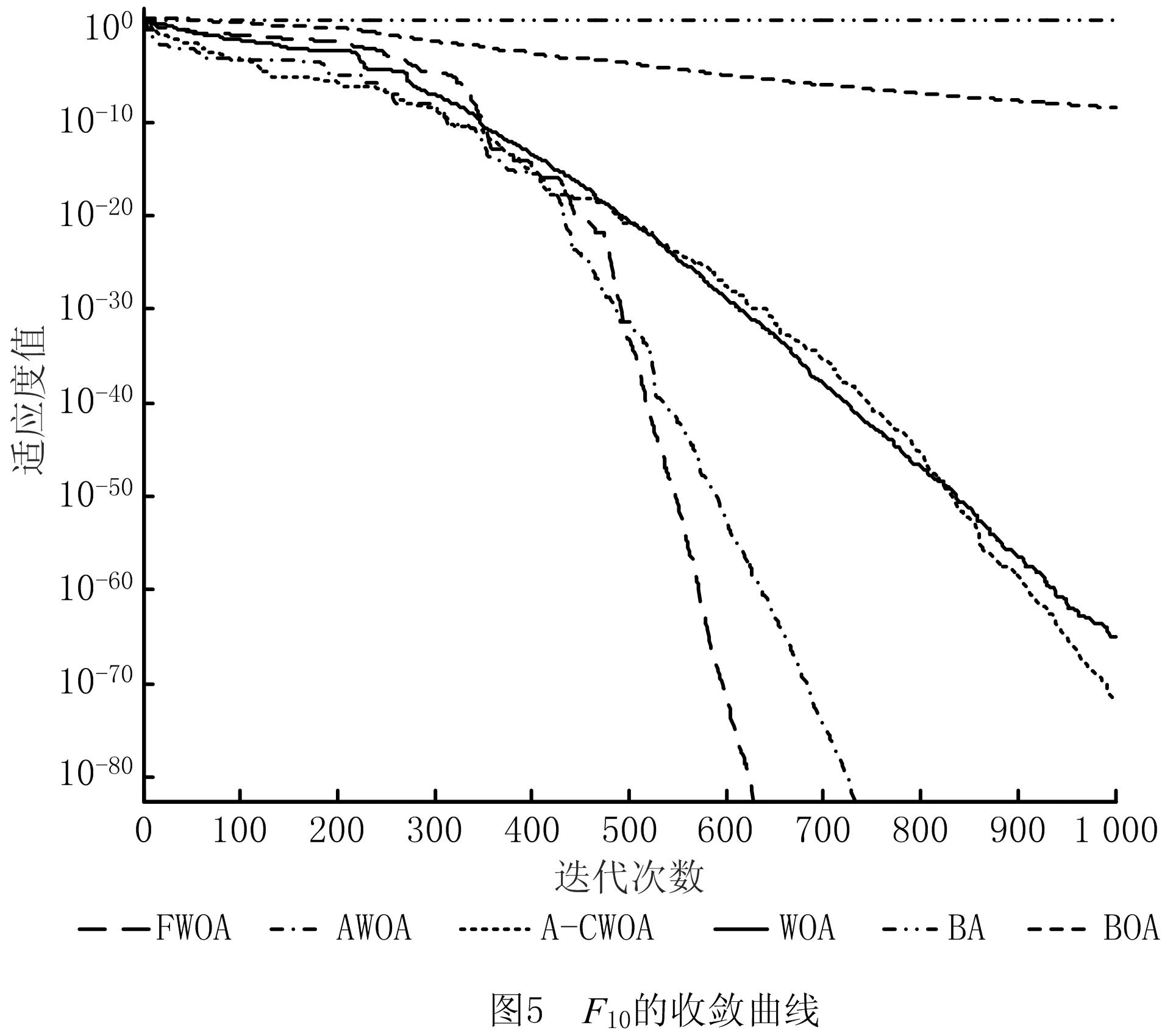
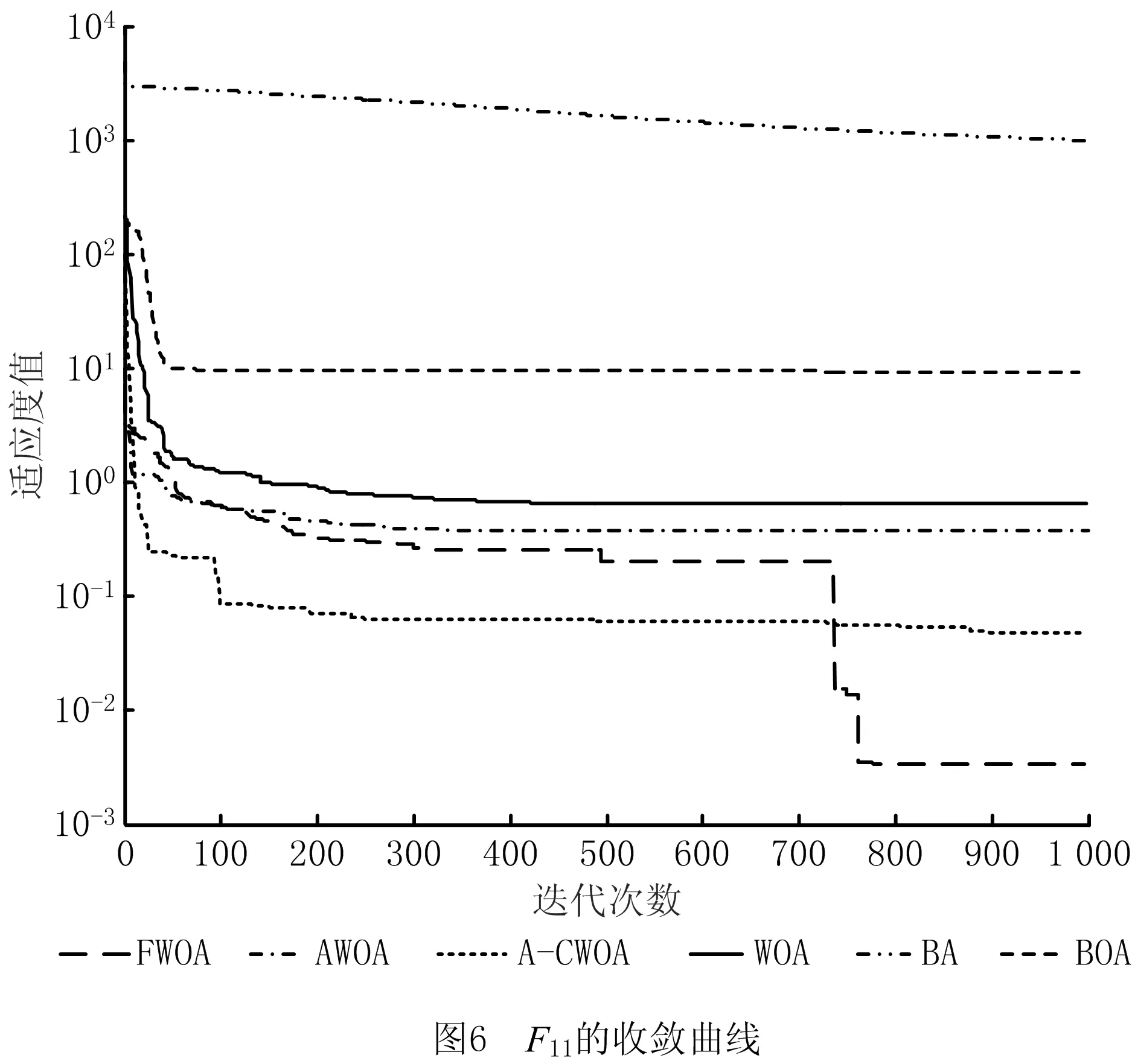

4.2 工程设计约束优化问题的求解与分析

5 结束语
