基于稀疏轨迹聚类的旅游目的地位置预测方法

刘 涵

(亳州职业技术学院 管理学系，安徽 亳州 236800)

经济全球化背景下，国家经济、社会发展以及人们的生活水平都在逐步提升，越来越多的人在工作之余更加注重精神享受。因此，近年来国内外旅游业迅速发展。在社会经济、交通、科技信息及环保理念的飞速发展下，可供选择的旅游景点越来越多，越来越多的人选择自驾游或与好友结伴旅游。为了更好地发展旅游经济，提升偏远地区经济水平，相关学者对旅游目的地位置预测进行了研究。温惠英等提出，在生成对抗网络中构建一个推荐模型，来预测某一阶段人们偏好的旅游目的地[1]；张志远等提出，面对移动对象的不确定性轨迹，在传统预测模型的基础上，引用社会特征分析行人注意力，构建行人轨迹预测模型[2]。通过对这两个预测模型进行使用测试，发现传统预测模型由于对旅游线路的聚类性能不佳，预测结果准确率不理想。

为解决上述问题，该文提出基于稀疏轨迹聚类的旅游目的地位置预测方法。当前，人们选择的出行时段、出行方式以及移动轨迹向着多样化发展，这些轨迹称为稀疏轨迹。稀疏轨迹聚类预测方法能够通过识别时空轨迹重复数据实现重复数据滤除，通过稀疏轨迹聚类可补全旅游目的地的预测轨迹，在迭代网络及预测轨迹的基础上实现旅游目的地位置预测，为旅游业的发展提供帮助。

一、旅游目的地位置预测方法

采集旅游者的空间走动轨迹时，需要剔除重复性数据，计算特征点到其余各点距离，将得到的特征点和不属于重复数据集合的点重新排序，实现对重复数据的识别与消除。对轨迹数据聚簇分类，并利用稀疏轨迹聚类算法，实现对稀疏数据的补全，采用多种熵估计方法，通过迭代网格对上述路径进行数据集合无用数据消除，实现基于稀疏轨迹聚类的旅游目的地位置预测。

(一)识别与消除时空轨迹重复数据

旅游者作为不断变化的移动对象，在采集他们的空间运动轨迹时会出现重复性数据。如旅游对象A去D1地点后，直接向D2点移动，然后再去D3和D4等地。但旅游对象由于自身喜好或其他问题，可能会返回到前几个已经去过的位置。因此，采集到的空间轨迹会存在重复，需要剔除这些重复性数据[3]。

将带有时间标识的空间位置序列定义为旅游对象的时空轨迹，P(sj)={p1(sj),p2(sj)，…，pn(sj)}为轨迹采样点，其中pi(sj)∈pn(sj)表示其中的任意一个采样点；n表示采样点数量；sj代表移动对象标识，存在S={s1,s2,…,sJ}，其中sj∈S表示移动对象集合中的任意一个；j∈J表示移动对象数量。利用经纬度、时间戳和移动对象标识来描述移动对象采样点，即存在：

pi(sj)=〈(xi,yi),ti,sj〉

(1)

公式中(xi,yi)表示轨迹点位置分量；ti表示时间戳[4]。将具有相同位置信息和相同时间信息的关于sj的轨迹点定义为重复数据，即该数据时间戳与经纬坐标完全一致，将此类数据合并处理。而在某一连续时间内，若关于sj存在多个轨迹点，且这些点若集中于特定的小范围区域内，则认为这些数据为隐含重复数据。当某一类移动对象sj的轨迹点集合为

P(sj)={pa(sj),pa+1(sj),…,pb(sj)}

(2)

公式中i∈[a,b]。若存在dis(pa,pi)≤2β,dis(pa,pb+1)>2β且tb-ta<βt时，则该集合为重复点集，则该集合P′(sj)∈P(sj)。其中：dis(*)表示距离函数，β表示轨迹方向参数。重复点集筛选如图1所示。

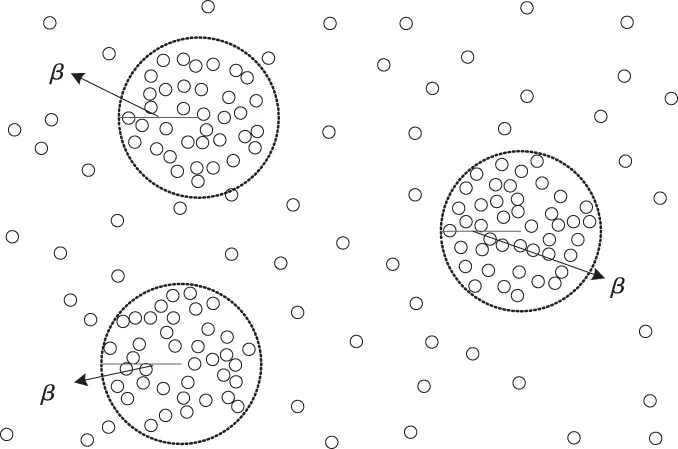
图1 重复点集合筛选示意

在重复点集合P′(sj)中，选择其中一个可以作为代表的轨迹点，即特征点，该点的基本信息获取结果为

zk(sj)=〈(xk,yk),ta,tb,sj〉

(3)

公式中ta表示重复点集合的初始时间，tb表示结束时间，(xk,tk)表示特征点的坐标。特征点提取如图2所示。

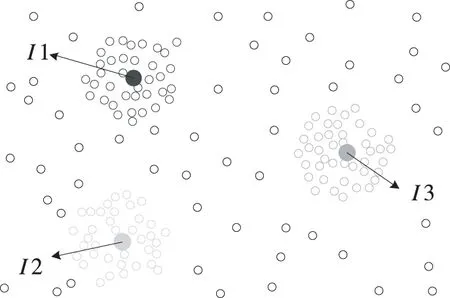
图2 特征提取示意

通过公式(3)可得到特征点到其余各点的距离，将得到的特征点及不属于重复数据集合的点重新排序，得到关于sj的新轨迹点序列，实现对重复性数据的识别与消除[5]。

(二)基于稀疏轨迹聚类补全稀疏数据

由于移动对象的移动数据具有稀疏性特征，在消除重复性数据后会存在数据缺失问题，进而影响最终的预测结果。因此，基于稀疏轨迹聚类算法可补全稀疏数据，提升数据质量。不同的旅游者在游玩的过程中会在一个固定的城区内形成历史轨迹点，而这些轨迹会受到移动对象性格、喜好以及偏爱的影响，具有一定的波动性。因此，基于上述假设聚类轨迹数据。稀疏轨迹聚类算法对稀疏数据的补全如图3所示[6]。

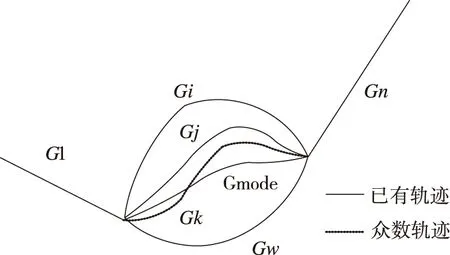
图3 稀疏轨迹补全示意

将聚簇内元素的众数，作为聚簇结果的代表值，进行初始化、距离计算样本聚簇和结果评估。在上一节处理完毕的数据集合中，随机选择个轨迹聚类中心，分别为c1,c2,c3,…,cn，其中ci表示向量，其长度为L，则ci=[p1,p2,…,pi,…,pl]，代表若干个移动轨迹。根据图3中的标注可知，轨迹集合有G={G1,G2,…,Gi,…,Gn}，该集合中的轨迹Gi={p1,p2,…,pi,…,Pl}。利用稀疏轨迹聚类算法计算中心轨迹与样本轨迹之间的距离，公式为

Dist〈Gi,Gj〉=max{f(Gi,Gj),f(Gj,Gi)}

(4)

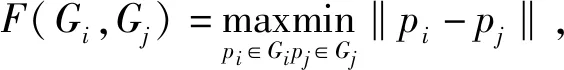
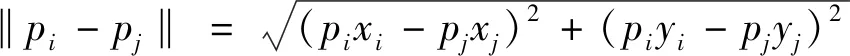
(5)

将样本Gj划分到距离最小的聚簇中，令同一组的轨迹距离尽可能缩小，不同组的轨迹尽可能扩大。样本划分完毕后，计算各组轨迹间的均方差和，利用下列公式评价聚类效果：

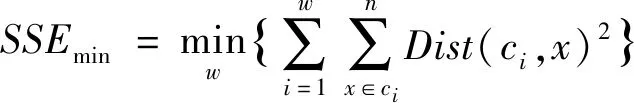
(6)

根据上述4个步骤实现对轨迹数据的聚簇分类，并利用稀疏轨迹聚类算法实现对稀疏数据的补全[7]。

(三)多种熵估计预测旅游目的地位置

在前文的基础上，通过稀疏数据的补全获取了旅游目的地预测位置的数据集合，此时集合中存在大量的冗余路径，不能作为最终的旅游目的地位置预测轨迹。为此，采用多种熵估计方法，通过迭代网格对上述路径进行数据集合，消除无用数据，得到准确的旅游目的地位置预测数据集合，有效解决旅游线路重复及旅游目的地位置预测效果不理想等问题。具体应用过程如下：

采用多种熵估计方法，预测旅游目的地位置。首先生成一个基于迭代网格和时间的轨迹序列，平均划分每一天，并保证其时间段不重叠，即得到的时间段集合为T={t1,t2,…,tn}，其中与时间段信息相关的原始轨迹为：

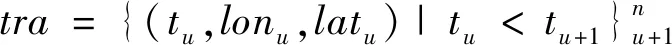
(7)

公式中，tra表示轨迹，tu表示时间节点，lonu表示经度值，latu表示纬度值，u∈n，表示个数。将tra中的所有节点映射到网格点和时间段上，生成带有时间标签的轨迹序列：

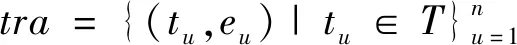
(8)

公式中，eu表示tu时段的轨迹在网格中的节点位置[8]。采用多种轨迹熵值预测旅游目的地位置，引入位置熵表示游客对某一旅游地点的喜爱程度。该值的计算公式为：

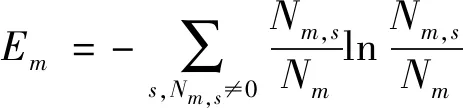
(9)

公式中，Nm,s表示旅游对象s访问旅游位置m时的次数，Nm表示所有用户访问旅游位置m时的次数。熵值越低说明可预测性就越强，反之则越低。时间熵可以描述某一时间段内游客在某区域内的活跃程度，则时间的熵值为：

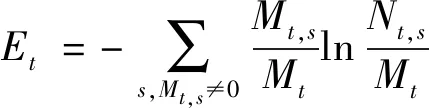
(10)

公式中，Mt,s表示旅游对象s在t时间段内访问的旅游位置总数量，Mt表示所有用户在同一时间段内访问的旅游位置总数量。生成轨迹序列后，利用一阶马尔可夫链量化轨迹规律[9-10]。马尔可夫链状态与每个网格中的轨迹对应，而轨迹从一个网格移动到另一个网格时，则为马尔可夫链的状态转换。根据已经给定的所有轨迹tra构造转移概率矩阵Z，生成马尔可夫链F(tra)，以此计算状态之间的转移熵，进而分析轨迹规律。用轨迹转移熵矩阵H表示所有状态之间的随机性：

Hi,j=H(Zi,j)=-∑i,jλZi,jlogZi,j

(11)

公式中，λ表示轨迹马尔可夫链F(tra)的平稳分布。已知转移概率矩阵Z，则用轨迹空间中网格i与j之间的移动数据除以所有网格之间的移动数目，得到网格i与j之间的转移概率：

(12)

公式中，Q表示网格，Len(tra)表示对马尔可夫链的量化结果。根据上述内容，通过多种熵估计结果，预测旅游目的地位置。二阶马尔可夫生成的用户轨迹预测模型见表1。

表1 用户轨迹预测模型

利用表1所示的预测模型预测旅游目的地位置轨迹。预测结果为

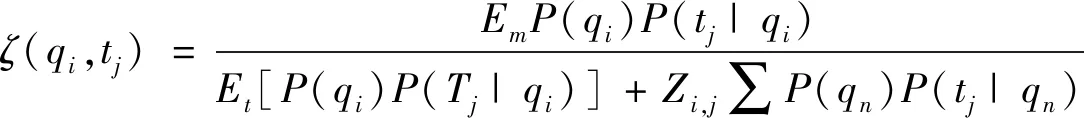
(13)

公式中qi、qn、tj分别为给出的网格和时间段集合中的任意数值。通过以上过程实现基于稀疏轨迹聚类的旅游目的地位置预测。

二、实验研究

通过对比实验比较基于稀疏轨迹聚类的位置预测方法与传统位置预测方法之间的差异性。

(一)算法性能测试

模拟设置若干个旅游目的地位置和旅游轨迹，通过实验对比方法和稀疏轨迹聚类算法，以各个时段的划分作为聚类标准，计算各个时段内的轨迹之间的距离平方差，图4为不同聚类值下求得的最小SSE值。

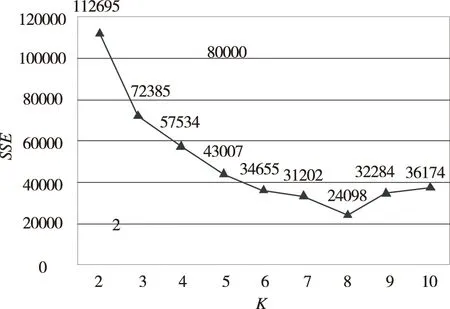
图4 不同K值下SSE值变化曲线

根据图4显示的曲线变化可知，当初始选择聚簇分组数为8时，SSE的取值结果最小，对应的聚类效果也最好。因此，该算法可将聚簇分组数设置为8，补全聚类前后的轨迹数量、轨迹点个数和单轨迹平均轨迹点个数的变化情况(图5)。

图5 聚类前后轨迹数据质量对比

从图5可以看出，通过重复性数据识别664 718个重复轨迹点之后，预测方法进行重复数据删除操作，得到8 364 012个有效轨迹点数，同时获得799 935条轨迹。然后利用稀疏轨迹聚类算法补全缺失数据，使有效轨迹点数增加了873 552个，轨迹增加了335 454条。可见该聚类算法提升了历史数据质量。

(二)对比测试

将提出的预测方法作为实验组测试对象，将两个传统预测模型分别作为对照1组测试对象和对照2组测试对象，模拟一条旅游轨迹(图6)。

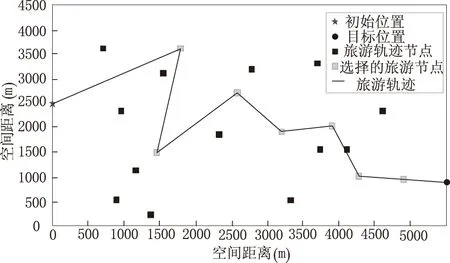
图6 轨迹预测标准

以图6中的轨迹为最终目标，图7为3个测试组的旅游目的地轨迹预测结果。

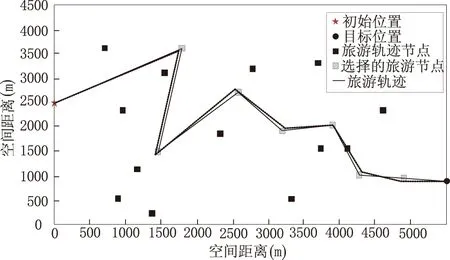
(a) 实验组测试结果

根据图中曲线走势可知，实验组的预测轨迹与图6所示的标准轨迹之间的偏离值更小，而两个对照组的预测轨迹与标准轨迹之间的偏离值更大。进一步计算预测轨迹与标准轨迹之间的偏离值，结果如表2所示。

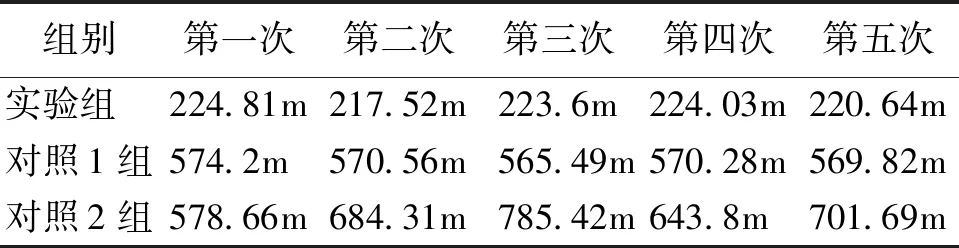
表2 平均偏离值计算结果

根据表中的计算结果可知，实验组的5组偏离数值均在200 m左右，对照组的5组偏离数值在500～800 m之间。经计算，5次测试下实验组的平均偏离值为222.12 m，对照组的平均偏离值分别为570.07 m和678.776 m。可见提出的预测方法效果更佳。

综上，该文提出的旅游目的地位置预测方法充分发挥了稀疏聚类算法的计算特征，实现了对复杂空间数据和时间数据的特征分析与挖掘。该方法利用稀疏轨迹聚类算法补全缺失数据，使有效轨迹点数增加了873 552个，轨迹增加了335 454条，说明该方法的聚类效果较好。5次测试下，该方法的平均偏离值为222.12 m，说明此方法能够提升旅游目的地位置预测效果。未来研究将继续降低预测轨迹与标准轨迹之间的平均偏离值，以期得到更好的旅游轨迹预测结果。