基于惯性/组合导航系统级故障诊断方法研究*

徐景硕 安 阳 嵇邵康

（海军航空大学青岛校区 青岛 266041）

1 引言

惯性导航系统（INS）作为一种全方位的自主式导航系统，它不受外界条件和环境的干扰，隐蔽性好［1］，在工业和军事领域得到广泛应用。尽管惯导系统导航信息精度高，但它的算法是一个积分过程，误差容易随时间积累，不满足续航时间长的飞行载体的要求。GPS系统精度较高，但使用权受制于人，而且它易受环境的影响，只能用做载体的辅助导航［2］。随着装备飞机导航系统的增多，通过SINS与其他系统的组合，可以解决其误差随时间积累的问题，输出更全面的导航信息，满足未来战机的需求；但由于装备载体系统的增加，故障发生的概率变大，当某一系统发生故障后会影响其他系统，系统整体的容错性下降。

为了解决以上问题，本文分两步来实现具有容错性的组合导航系统。首先设计一个无重置结构的滤波器，然后在子滤波器的输出后增加故障检测模块，用状态χ2检验法和残差χ2检验法［3］对故障进行检测，并比较它们的检测效果。

2 系统方案设计

2.1 具有故障检测功能的SINS/GPS/ADS/MG组合导航系统结构

为提高系统的容错性和计算能力，设计一个无复位结构的联邦滤波器［4］，对惯导、卫星导航、大气机、磁航向仪四种导航信息融合。其导航系统结构如图1所示。

图1 基于联邦滤波的容错组合导航结构图

该系统是以惯导为参考系统，将它与其他系统对同一导航参数的差值给子滤波器。各滤波器独立计算，互不影响，在同一时刻将结果给主滤波器［5］。主滤波器做融合计算，得到最终的估计值。在此基础上，给每个子滤波器的输出加上故障检测模块，用它来检测系统是否发生故障，以决定子滤波器量测信息是否有效。当诊断出某一子系统发生故障，主滤波器不接收其输出，重组剩余的系统，保证整体系统的正常工作。

2.2 信息融合方法

1）信息分配原则

为了合理地分配惯导信息，使不同性能的子滤波器精度均令人满意，将系统的过程信息Q-1和P-1按以下原则在主滤波器和子滤波器之间分配［5］：

系统满足信息守恒定理：

2）系统算法原理

（1）各子滤波器滤波过程包括两步［6］。

①时间更新

②量测更新

2）假设一共有N个子滤波器，主滤波器融合算法为

2.3 故障诊断方法

2.3.1 状态χ2检验法

状态χ2检验法是通过两个不同的估计值之间的差异判断系统是否发生故障［7］。第一个状态估计值X1(k)是经过Kalman滤波计算得到的，第二个状态估计值X2(k)是由上一时刻的估计值递推计算得到的预测值。

定义估计误差e1(k)和e2(k)为

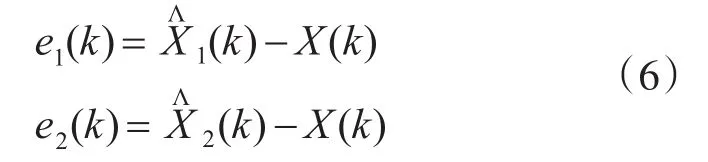
并定义：

当系统正常时，β(k)的均值为0；当系统出现故障时，β(k)Tk的均值不为0。因此，通过对β(k)均值的检测便可判断系统是否发生了故障。

利用统计学及二元假设的理论，可以推导得到以下故障检测函数：

式中，λk服从自由度为n的χ2分布。

故障判定准则为

其中，TD是设定的门限，合理地选取门限可以使系统的漏检率最小。

2.3.2 残差χ2检验法

为了减小故障检测算法的计算量，提高计算效率［7］，以下介绍一种残差χ2检验法来对故障进行检测。它的检测思路是通过对量测值和预测值(k/k-1)之间的差值d(k)（残差）是否满足零均值高斯白噪声来判断系统是否发生了故障［7］。

首先由k-1时刻得到k时刻状态的预测值为

由状态的预测值得到量测的预测值为

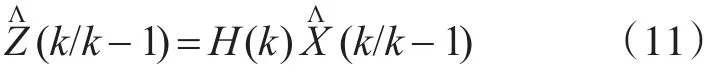
两者的差值即残差值为

当系统正常时，残差的均值为0；当系统出现故障后，其均值不为0。

同状态χ2检验法类似，残差χ2检验法的故障检测函数为

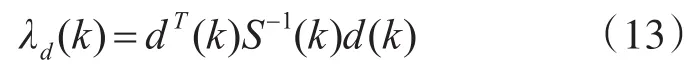
其中，λd(k)是服从自由度为m的χ2分布，即λd(k)～χ2(m)。m为测量Zk的维数。

故障判定准则为

3 仿真验证

以SINS/GPS为例，在GPS的量测值上设置故障，比较状态χ2检验法和残差χ2检验法对故障的检测效果。

3.1 仿真条件

1）门限的设置

状态χ2检测中取误警率α=0.005，设置的门限值如下：GPS/SINS：。

残差χ2检测中取误警率α=0.05，设置的门限值如下：GPS/SINS：。

2）故障的设置

在各子系统的量测值上设置两种故障：一种是突变的故障［8］，即在各量测值上加入比实际误差扩大10倍～20倍的常值偏置；另一种是缓变的故障［8］，可以用一阶或二阶的信号来表示。

3.2 仿真结果

检测的结果如表1和图2所示（*号表示存在漏检，0表示无故障，1表示有故障）。

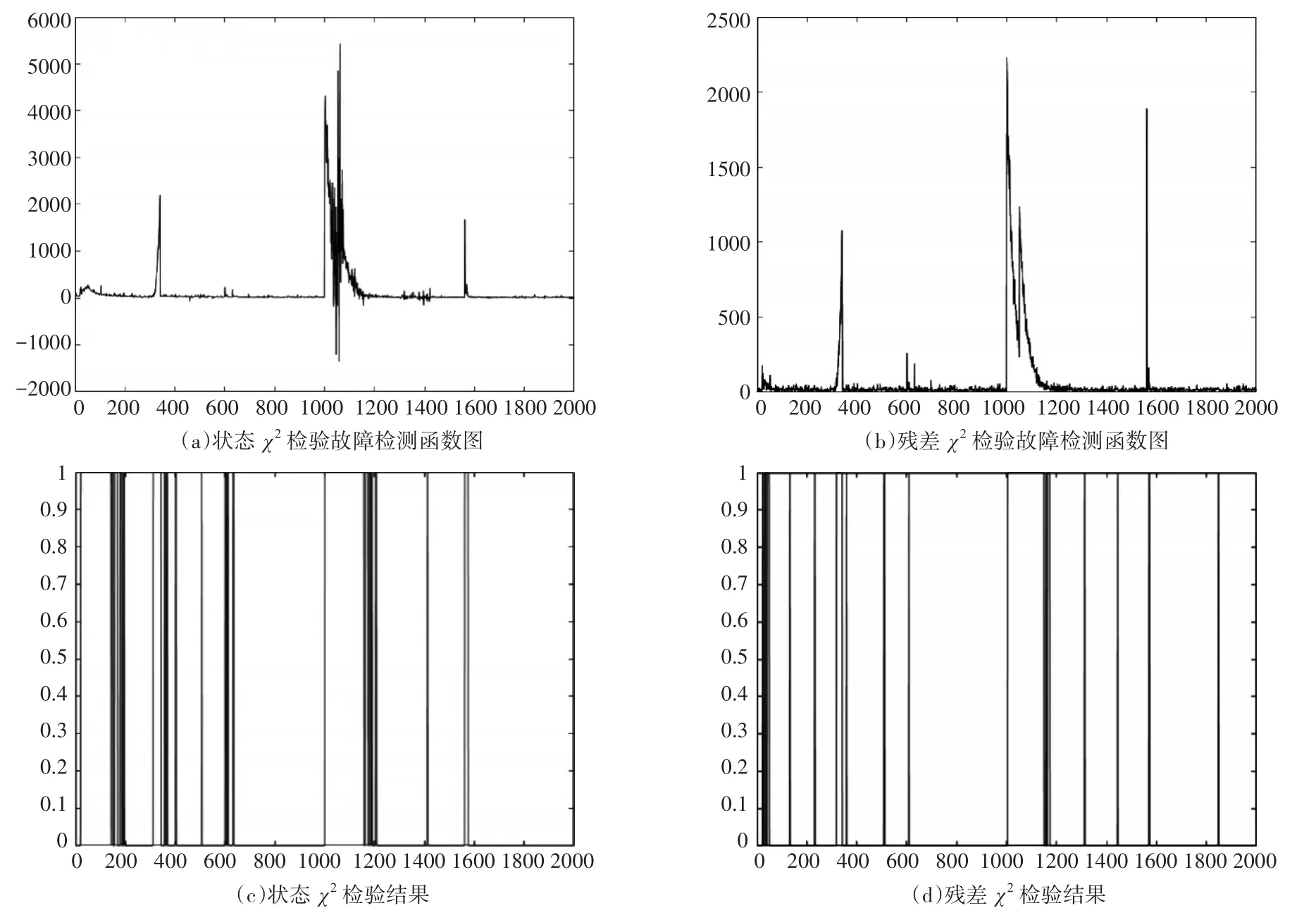
图2 故障检测曲线

表1 对子系统故障的设置及检测结果

3.3 仿真结果分析

状态χ2检验法和残差χ2检验法均可有效地检测出故障［9］。状态χ2检验法较为灵敏，当系统发生故障时能快速检测出故障，当它在告警开始和告警结束中间延迟较大，且随着时间增加，灵敏度有所下降。残差χ2检验法告警延迟小、计算量小，但它在中间阶段存在漏检的情况［10］，而且它对软故障的检测效果不好。

4 结语

本文首先用无复位联邦滤波结构设计组合导航，以提高系统的容错性和计算速度。然后针对系统常见的两种故障，对其检测方法进行了研究。通过比较状态χ2检验法和残差χ2检验法，得出状态χ2检验法对两种故障的检测效果都很好，但由于系统噪声、初值误差的影响使状态递推器误差扩大，后期故障检测效果降低［11］。相比状态χ2检验法，残差检验法χ2对故障检测效果更灵敏，计算量小，但是其对软故障的检测效果不好，而且存在漏检的情况。综合来看，在实际的应用中，可以综合传统的两种方法或者对现有的检验方法改进，弥补它们在实际应用的困难。对于状态χ2检验法，可以增加一个状态递推器，通过选取合适的周期用Kalman滤波器来重置两个状态递推器，避免已受污染的状态递推器污染整个系统［12］。此外，对于缓变故障的检测，可以对残差χ2检验法改进，在故障发生的早期，及时提取故障的特征［13］，及时地检测并排除故障，优化系统重组的流程，提高系统整体的容错性。