基于3×3耦合器的信号幅值系数调整研究*

汪云云 黄俊斌 顾宏灿

（海军工程大学兵器工程学院 武汉 430033）

1 引言

光纤光栅激光传感器凭借其体积小，抗电磁干扰以及高灵敏度等可实现多基阵组合和高精度探测，已广泛应用于应变、磁场、气体、温度、声压等微弱信号的测量中［1～7］。待测物理量作用于传感器的敏感元件上改变了敏感元件的物理特性，导致激光波长发生变化，再经由干涉仪结构将变化的波长量转为光强信号的相位差值；探测并解调变化的光强信号，即可获得待测物理量。干涉解调法借助干涉仪实现微弱波动信号高灵敏，宽范围以及高分辨率的测量，是信号解调技术中广受应用的一种方法。目前，相位生成载波（Phase Generated Carrier，PGC）及基于3×3耦合器的解调方法是干涉解调法中应用最成熟的技术［8～10］。PGC是在干涉仪上加载幅值较大的高频相移调制，结合贝塞尔函数分离出被测信号再进行后续解调，该算法因受载波信号的频率需求而限制了传感器的频率范围，面向数字化解调系统仍需要较高的采样率才能满足应用［11～14］。基于3×3耦合器的解调方案无需借助载波调制，利用3×3耦合器的固有特性能够实现灵敏度、动态范围以及解调性能的高优势，在噪声以及成本方面也能得到有效降低［15］。然而，基于3×3耦合器面对的最大困境是实际工艺水平无法保证3×3耦合器的理想对称性，而上述解调算法的优势也只有在对称情况下才能得以充分发挥。因此，为充分利用其固有优势，工程应用中只有选用分光比比较均匀的耦合器才能确保解调性能不受耦合器相位偏差影响，但3×3耦合器输出的干涉信号幅值仍无法通过元件得到有效改善，因此，针对其输出干涉信号幅值进行调整以满足工程应用条件是改进现有算法的核心内容。本文将针对现有的两种调整方式进行详细说明，对比两种方式的解调效果及其适用领域，并进行总结和展望。

2 基于3×3耦合器的基本解调原理

采用3×3耦合器的干涉仪解调系统凭借其输出信号的相位特定关系，通过数学运算即可完成解调。对于理想的3×3耦合器，其输出的3路光信号经过光电转换后是完全对称的，即输出信号的幅值相等，彼此相位相差120°。A/D采样后的输出表达式为

式中φ(t)为待检测信号，其中φ(t)=2πnLΔv/c，n为光纤的纤芯折射率，L为干涉仪非平衡路径长度，Δv则是激光的频率变化表示，a为干涉条纹对比度，a近似为1。

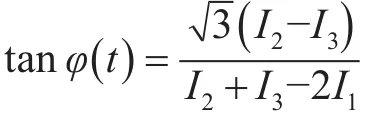
图1 基于3×3耦合器的NRL算法框图

图2 基于3×3耦合器的对称解调算法框图

基于上述几种3×3耦合器的解调算法分析，其均有一共性：面向3×3耦合器理想对称才能满足较高的解调性能和测量精度，而工程应用中，选用分光比较均匀的耦合器尚且只能满足输出相位差近似对称于120°，能实现在幅值对称条件下不对解调效果造成任何影响［16］。

3 面向非对称3×3耦合器的幅值系数调整原理

实际应用中选用分光比较均匀的耦合器时，探测器接收到的干涉信号应表示如下：

因分光比较均匀的耦合器输出的相位差值与理想值偏离1°，该偏离不影响解调效果，因此式（2）中近似等于120°。比较式（1）与式（2），发现三路输出信号幅值Dm与Em均不再相等，如果不加以调整，后续的解调过程也无法进行。因此，准确获取Dm、Em的值也是后续幅值参数调整的关键。现阶段，干涉信号幅值非对称问题常用的调整方式有PZT（压电陶瓷）调制和椭圆拟合估计参数法。

PZT调制源自于PGC解调方案中的一种调制方式。此处，其主要是在干涉仪一臂的PZT（压电陶瓷）上加载幅度值足够大，且能够形成调制周期大于2π相位变化的正弦信号，以此囊括每个周期内干涉信号的最大值与最小值，通过提取干涉信号中的最大和最小值可获取每路干涉信号的直流分量Di以及交流分量幅值Ei［14］：

再将求出的每路Di与Ei代入式（2），可将每路输出干涉信号减去各自的直流成分Di后，再将三路的Ei进行系数调整：例如乘以不同的增益系数：ki=E1/Ei，使得每路干涉信号中的交流分量幅值均相等，即满足了解调过程所需的对称性，能满足3×3耦合器解调算法的后续解调需求。

椭圆拟合参数估计法是因输出干涉信号中任两路可组成椭圆函数，再以最小二乘法拟合出该两路信号中的幅值参数，以此可以得出每路输出干涉信号的幅值参量［17～20］。具体过程如下：任选式（2）中的两路组成的椭圆方程式：

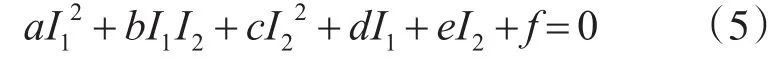
式（5）中椭圆幅值系数（a，b，c，d，e，f）可经由最小二乘法拟合给出，为了得到干涉信号各路幅值参数需将式（2）与椭圆函数式（5）进行椭圆函数系数对比，得出所选干涉信号的幅值参数：

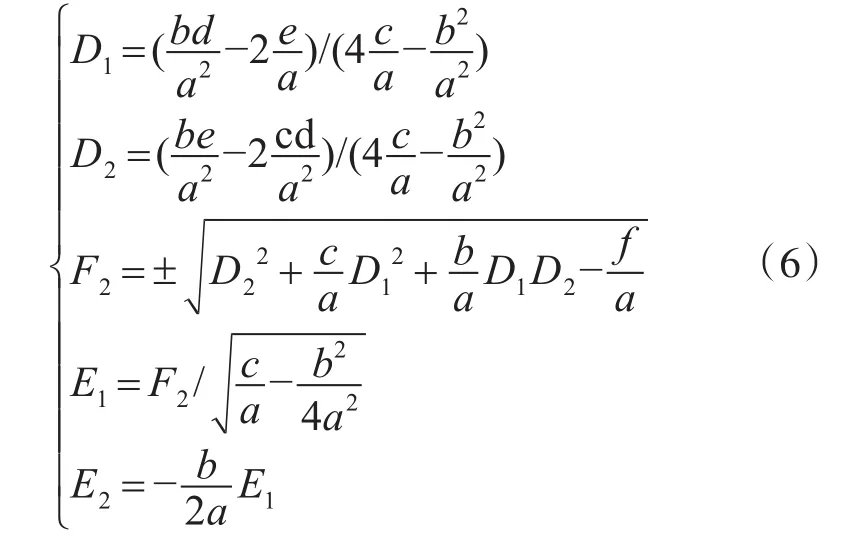
再将式（6）中各项幅值参数代入式（2），再将直流成分去除，调整干涉信号中的交流分量幅值系数，最终得到相位信号的正弦和余弦形式，再将其微分交叉相乘并积分后可得出相位信号：

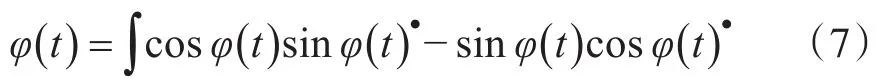
4 实验与分析

为对比以上两种不同调整方式的解调效果，搭建了以迈克尔逊干涉仪为例的解调系统图，如图3所示。

图3 基于迈克尔逊干涉仪的解调系统图

如图3所示，980泵浦作为系统的光源，可提供连续、稳定的单模激光输出，再经980/1550波分复用传输至光纤光栅激光传感器，将满足1550波长段的激光反射回来，与此同时，若传感器承载着待测信号，反射回来的激光信号将携带该被测信号导致的波长偏移量；再经过波分复用1550端口进入隔离器，后续再传输至迈克尔逊干涉仪中，最终，光电探测器接收光信号并转换为电信号，经采集后可解调处理该输出信号。

实验中，在基于采样频率为125khz情况下，PZT调整方案中采用的频率以及幅值为2KHZ，5V以此来满足该方案所需的一个周期内的包络需求进行系数调整，从而获取每个周期内干涉信号的直流以及交流幅值参数，在外加2KHZ的振动信号下，其解调效果图如图4所示。椭圆拟合估计参数法则是在2KHZ的振动信号下直接进行椭圆参数拟合估计解调，因输出干涉信号中受外界环境等影响，因此需要将拟合的椭圆进行形态学分析，再结合canny算法获取椭圆边界，后续再以最小二乘法拟合椭圆，最终通过计算对比获取干涉信号的各项幅值参数进行解调，其解调效果如图5所示。

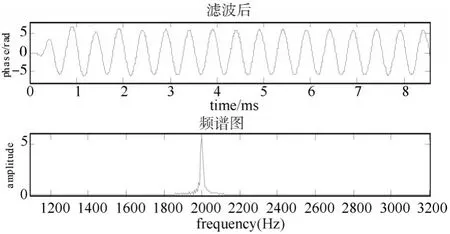
图4 PZT调制调整幅值系数的解调效果

图5 椭圆拟合参数估计法调整系数的解调效果

对比图4与图5的解调效果的一致性很好，解调效果相差甚微。以上两种方式从不同方面体现了对干涉信号幅值参数的获取，PZT调制法需要外加PZT元件置于干涉仪中，同时调制信号的幅值以及调制周期需满足包络要求才能准确获取所需参数。椭圆拟合估计法的核心是干涉信号组成的李萨茹图形的椭圆方程是否准确，其准确性决定着最终解调效果性能；与此同时，其易受偏振影响，解调复杂度较于PZT调制法更高。

5 结语

面向实际工程应用中无法避免的3×3耦合器非对称问题，对比了两种不同方式的幅值系数调整算法，就其解调效果而言，两种方式的解调效果一致性比较高，但其解调复杂程度以及受外界因素干扰影响能力以及适用平台存在一定差异，PZT调制法则相对比较稳定，但其需外加载波调制，限制了自动化以及小型化平台的应用；椭圆拟合参数估计法则无需外界调制，但其拟合的椭圆方程的准确性决定着后续解调优劣性，而由输出原始信号不仅仅包含被测信号还包含外界干扰等波动信号，无法保证干涉信号的准确性，这在很大程度上提升了解调的复杂度。