新型DKT组合薄壳单元及对侧翻一步碰撞算法的改进*
2021-08-12陈轶嵩刘永涛
王 童,陈轶嵩,刘永涛
(长安大学汽车学院,西安 710064)
前言
汽车保有量急剧上涨,人们出行生活越来越便利[1]。同时,恶劣交通事故数量呈现逐步上升趋势,给乘客生命财产带来重大损失[2]。其中,客车侧翻常造成群死群伤的严重后果,是最严重的交通事故类型之一[3]。如何最大限度预防侧翻事故的发生,加强客车结构侧翻碰撞安全性研究,不断提高客车侧翻碰撞安全性能,已成为全社会共同关注并努力解决的重要问题之一[4]。
客车侧翻一步碰撞算法,是参考板料冲压一步成型算法思想,提出的一种用于客车侧翻碰撞模拟分析的新算法[5]。借鉴该算法核心思想,侧翻一步碰撞算法同样基于塑性全量理论,利用侧翻碰撞过程中能量的转换关系。与现有LS⁃DYNA等增量法软件相比,在略微牺牲一点计算精度情况下,大幅提升了计算效率。算法可在车身设计初期,对结构侧翻碰撞安全性进行快速评价,缩短产品开发周期,同时,可为后续针对客车侧翻安全性的灵敏度分析、参数优化和拓扑优化算法研究提供必要支撑条件[6]。
在有限元数值模拟过程中,不同单元模型选择会对算法计算结果和效率产生较大影响[7]。因侧翻一步碰撞算法基于塑性全量理论,车体骨架由若干大几何尺寸薄壁杆件构成,侧翻碰撞过程主要受力特性为弯曲,故所有膜单元及比较简单的三角形薄壳单元均无法满足计算要求[8]。作者在客车侧翻一步碰撞初始算法中采用了四节点Mindlin组合壳单元作为分析单元类型。为进一步提高算法计算精度和效率,对四节点薄壳单元进行翘曲修正改进,基于改进后的四节点薄壳单元和塑性全量理论,将DKT(discreted kirchhoff theory)四节点薄板单元和传统四节点等参膜单元组合,构造一种新型四节点DKT组合薄壳单元,替代初始算法四节点Mindlin组合壳单元,对侧翻一步碰撞算法改进。预计改进后算法在模拟效率基本不变的同时,计算精度得到一定程度的提高。
1 侧翻一步碰撞算法基本理论
客车侧翻一步碰撞算法[9],基于非线性全量理论和比例加载假定,依据ECER66法规[10],忽略中间状态和构形变化[11],只考虑结构碰撞开始和最大变形两个状态。根据车体侧翻碰撞过程运动变形特点和能量转换关系,得到满足变形条件的初始解,采用Newton⁃Raphson法迭代求解[12-13],快速获得结构最终变形。
将碰撞开始状态结构作为初始构形{X0}。此时车体未发生变形,结构动能Ed为

式中:M为车体质量;Δh为车体质心下降高度;J为车体绕假定转轴转动惯量;ω为车体角速度。
碰撞开始状态结构各节点速度{v0}为

式中:ri为各节点到侧翻假定转轴的距离;n为节点数。
在结构最大变形状态,车体结构产生明显变形。侧翻一步碰撞算法中,结构最大变形不确定,需假定一个最大变形构形{x0}。各节点位移{U0}为

车体结构动能Ed在碰撞中主要转换为结构形变能,结构形变能W为[14]

式中:{ε}为单元塑性应变;{σ}为单元塑性应力;Ve为单元体积;N为单元数。
判断结构形变能W与车体动能Ed是否满足式(5)能量关系假定:

若不满足,则对节点位移{U0}进行修正,按照式(4)重新计算结构形变能。将满足式(5)能量关系假定的节点位移{U}作为Newton⁃Raphson迭代初始解。
对满足能量转换关系初始解{U},节点失衡力{R(U)}已处于不平衡状态:
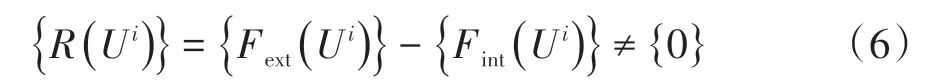
式中:{Fext(Ui)}为广义失衡外力;{Fint(Ui)}为广义失衡内力。
应用Newton⁃Raphson法,解决节点失衡力不平衡问题。对初始解{U}按式(7)和式(8)迭代求解,使式(6)达到平衡,得到结构最终变形。

2 四节点薄壳单元翘曲修正改进
客车侧翻碰撞结构变形过程中,部分结构可能存在变形过大问题,导致较明显单元翘曲[15],影响算法计算精度。对所有四节点薄壳单元,首先考虑单元翘曲修正问题,对其进行改进,接着建立本文所需四节点DKT组合薄壳单元模型,对侧翻一步碰撞初始算法进行改进。
2.1 考虑翘曲修正的四节点薄壳单元坐标转换关系
提取四节点薄壳单元中性层。在整体坐标系下,产生翘曲的四节点单元中性层为i'j'k'l',各节点坐 标 为i'(Xi',Yi',Zi')、j'(Xj',Yj',Zj')、k'(Xk',Yk',Zk')、l'(Xl',Yl',Zl')。将翘曲后单元中性层,以对角线i'k'作为轴线,分割为两个三角形Δi'l'k'和Δi'j'k',展开到过k'点、以n→为法向量的平面内,可以得到不产生翘曲的四节点单元i'j″k'l″,如图1所示。

图1 四节点薄壳单元中性层翘曲展开前后示意图
整体坐标系内,翘曲单元4个节点坐标均已知。对于三角形 Δi'j″k',边长Li'j'=Li'j″、Lk'j'=Lk'j″、Lk'l'=Lk'l″、Li'l'=Li'l″及轴线Li'k'长度均可计算。
2.2 基于形心位置不变假设的最终展开构形
翘曲四节点薄壳单元在展开前后形心位置保持不变。在整体坐标系内,将展开后的四节点单元形心平移至展开前初始位置。由于单元翘曲时形心位置,在单元展开后已发生变化,需将其平移至展开前位置。以展开后四节点单元i'j″k'l″形心为基点,因展开后四节点单元形心需积分,计算不便,故将单元各节点坐标平均值近似作为形心O″,如图2所示。

图2 整体坐标系下展开后单元形心平移示意图
因翘曲单元i'j'k'l'形心无法准确确定,故本文以翘曲单元各节点坐标平均值为近似形心O',将展开后四节点单元形心O″平移到翘曲展开前点O',得到最终翘曲修正单元构形。翘曲展开后单元形心O″坐标为

翘曲单元展开前形心O'坐标为

可得平移形心后四节点单元ijkl各节点坐标为

式中ξ分别取i、j、k、l,ς分别取i'、j″、k'、l″。
经过上述计算过程,可对已发生翘曲四节点薄壳单元进行修正,在整体坐标系内获得翘曲修正改进后单元(中性层)各节点坐标。
3 改进的四节点DKT组合薄壳单元构造及对侧翻一步碰撞初始算法的改进
对经过翘曲修正的四节点薄壳单元,为便于计算单元应力应变和节点内力,须重新将整体坐标系下翘曲修正改进后的单元各节点坐标转换至局部坐标下,进行算法后续计算过程[16]。
3.1 四节点DKT薄板单元
离散Kirchhoff理论基于以下基本假定:(1)单元中面的垂直法线,变形前后仍与中面垂直,且长度不变;(2)单元厚向应变εz=0,厚向应力σz=0,切向应力γxz=0、γyz=0。
在上述基本假定基础上,建立基于离散Kirchhoff理论的四节点薄板单元。单元局部坐标系内,模型约定仅单元4个角节点和4条边的4个边中节点保持Kirchhoff直法线假设,且每个角节点有自由 度(wξ,θξx,θξy)(ξ=i,j,k,l),边 中 节 点 有 自 由 度(θςx,θςy)(ς=i',j',k',l'),如图3所示。

图3 离散Kirchhoff理论节点自由度假设
四节点DKT薄板单元中性层内任意一点转动自由度θx和θy可由单元4个角节点进行插值,即

式中 :{}为单 元各节 点自由 度{wi,θix,θiy,wj,θjx,θjy,wk,θkx,θky,wl,θlx,θly}T,且有[Hx]=[Hx1Hx2...Hx12],[Hy]=[Hy1Hy2...Hy12]。
四节点DKT薄板单元Bb矩阵为

其中

3.2 四节点等参膜单元
对侧翻碰撞过程中单元拉伸效应,本文中选择双线性四节点等参膜单元模拟,各节点自由度向量如图4所示。

图4 四节点等参膜单元示意图
经等参变换后单元形函数为

式中ri和si(i=1,2,3,4)为经过等参变换后各节点的自然坐标,其值为±1。
四节点等参膜单元B m矩阵为

3.3 基于塑性全量理论的节点广义内力计算
将上述3.1节部分所获四节点DKT薄板单元和3.2节部分所获四节点等参膜单元B矩阵进行组合,得到所需四节点DKT组合薄壳单元。将其应用于基于塑性全量理论的侧翻一步碰撞算法,计算客车侧翻碰撞过程产生的单元变形及各节点广义内力。
3.3.1 塑性应力计算
左Cauchy⁃Green变形矩阵逆阵[G]-1为

其中

对空间四节点DKT组合薄壳单元内部任意一点i,由于受到弯曲变形影响,该点所在横向上任意一点位移不同。令薄壳厚度为t,为计算单元应变、应力及节点广义内力,经对多组方案对比分析,本文在单元厚向选择5点高斯积分[17],各积分层均采用全积分方式,对板弯曲和膜拉伸两种变形同时进行考虑,如图5所示。

图5 薄壳单元的向量关系示意图
四节点等参膜单元内部任意一点位移,可由位移插值函数计算:

四节点DKT薄板单元内部任意点转动自由度θx和θy可由单元4个角节点进行插值,由式(12)计算。在图5中,L1、L2、L3、L4、L5为5点高斯积分求积位置因 子 ,数 值 分 别 为0.906 179 85、0.538 469 31、0、-0.906 179 85、-0.538 469 31。
各积分层单元局部坐标系下各个方向对数应变为[18]

单元各积分层面内或弯曲变形产生的塑性应力σs1、σs2、σs3、σs4、σs5可由式(21)计算[19],其中σs3为膜应力,σs1、σs2、σs4、σs5为板应力。

3.3.2 节点广义内力计算
由3.3.1节部分所获各积分层塑性应力,各积分层广义内力为

单元各节点广义内力可对各积分层广义内力组合得到,即

应用坐标转换矩阵[T]-1可将局部坐标系下单元各节点内力及内力矩转换至空间坐标系下,即

其中

车体结构各节点广义内力向量{F}int可由空间内各单元节点广义内力累加,即

接着可对初始解各节点广义失衡力进行Newton⁃Raphson迭代,得到算法所需结构最终变形。
4 应用实例
为检验本文所提新型DKT组合薄壳单元对客车侧翻一步碰撞初始算法改进的有效性,以某企业实际开发的一款12 m公路客车典型车身段作为分析对象,通过对车身段模型适当简化,将侧翻一步碰撞改进算法与初始算法、LS⁃DYNA和实车试验结果进行对比,检验所提单元模型实际效果。
车身段试验模型如图6所示,试验模型基本参数如下:总质量2 409 kg,质心离地高度1.5 m,X方向距离前端面为0.937 m,Y方向为0.012 m,如表1所示。

表1 典型车身段基本参数

图6 典型车身段模型示意图
车身段侧翻临界角为39o。参照典型车身段试验模型,简化后典型车身段结构有限元模型如图7所示。共离散四节点单元259 976个,节点258 368个。黄色部分结构为车身骨架结构,绿色部分结构为侧翻翻转支架结构,红色部分为乘员生存空间。与侧翻试验模型相同,计算模型骨架及侧翻翻转支架结构材料均选用Q345钢,材料弹性模量E=2.06×1011Pa,泊松比μ=0.3,密度ρ=7800 kg/m3,屈服强度σs=345MPa;乘员生存空间为刚性材料,密度取值尽量小,ρ=10 kg/m3,以免影响模拟结果精度[20]。

图7 典型车身段有限元模型
图8所示为应用所提新型DKT组合薄壳单元改进的侧翻一步碰撞算法(以下简称“改进算法”)模拟的结构最终变形云图。图9所示为初始算法模拟的结构最终变形云图。图10所示为LS⁃DYNA仿真的结构最终变形云图。图11所示为侧翻试验结构变形结果图。

图8 改进算法模拟结构最终变形云图

图9 初始算法模拟结构最终变形云图
图10 LS⁃DYNA仿真结构最终变形云图

图11 典型车身段侧翻试验结构最终变形
将图8~图11进行对比可以看出,4种模拟方式所得结构最终变形形态趋势基本吻合,应用所提新型DKT组合薄壳单元对侧翻一步碰撞算法进行改进,在实际工程应用中具有一定合理性。
为使上述对比结论更具说服力,需对4种方式结构最终变形定量对比。车身段侧翻碰撞过程中,底架结构几乎不产生变形,且与乘员生存空间的侵入量无直接关联。在企业对该车身段模型侧翻试验中,为获得结构变形数据,在典型车身段封闭环①和②两侧立柱内表面各选取11个测点进行数据采集。上述4种方式各立柱变形量如表2所示。
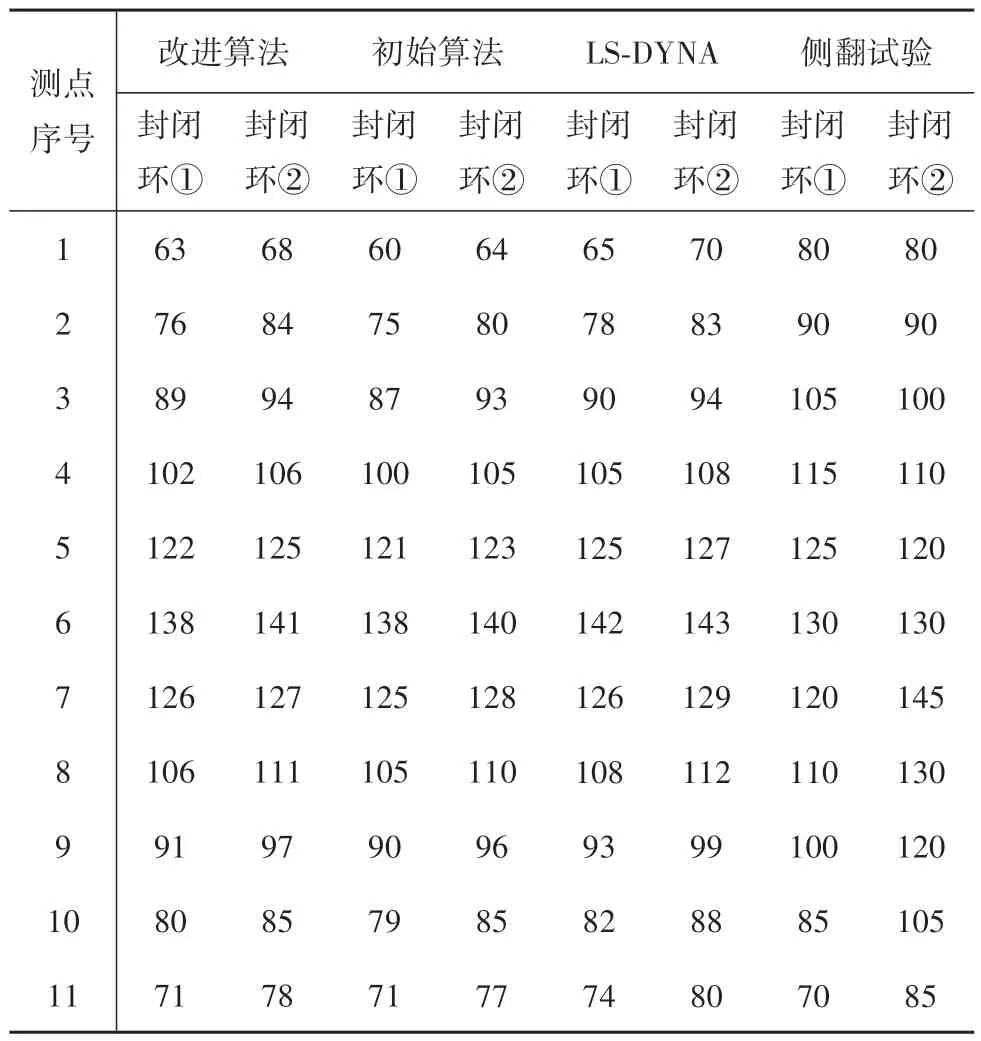
表2 各封闭环两侧立柱变形量统计 mm
图12和图13所示为典型车身段封闭环①和②两侧立柱变形量对比柱状图。

图12 封闭环①两侧立柱变形量对比

图13 封闭环②两侧立柱变形量对比
从图12和图13可看出,受试验制备及实际测量过程误差的影响,侧翻试验数据在稳定性方面波动相对较明显,但对改进算法实际应用有效性检验,具有一定工程参考价值。通过对比分析发现,4种方式所获结构各测点数据走势基本一致,验证了结构最终变形趋势吻合的结论。改进算法与LS⁃DYNA平均误差约为1.9%,精度略有牺牲,但比初始算法提高约1.5%;与侧翻试验平均误差约为7.1%,小于有限元工程计算误差经验值范围(即15%),计算精度在实际工程接受范围内。
接着对算法模拟效率进行对比。将侧翻一步碰撞改进算法模拟效率与初始算法及LS⁃DYNA进行对比,对比结果如表3所示。

表3 模拟效率对比
从表3可看出,改进算法模拟时间比初始算法稍快4 min,改进算法模拟时间约为LS⁃DYNA的1/10,初始算法约为LS⁃DYNA的1/9,改进算法模拟效率有一定提升。结合立柱变形量对比结论,改进算法在模拟效率些许提升的同时,计算精度也有一定程度的提高,可在客车结构设计初期,更快更准确获得侧翻碰撞结构最终变形,对结构侧翻碰撞安全性进行快速评价,缩短产品开发周期。同时,可为后续针对客车侧翻安全性的灵敏度分析、参数优化及拓扑优化算法研究提供必要支撑条件,检验了本文所提新型单元实际效果和工程应用价值。
5 结论
针对客车侧翻碰撞结构变形模拟过程中,因部分结构变形过大导致的单元翘曲问题,先对四节点薄壳单元进行了翘曲修正。接着,在翘曲修正后薄壳单元中性层基础上,基于塑性全量理论,将四节点DKT薄板单元和四节点等参膜单元进行组合,获得新型四节点DKT组合薄壳单元,替代侧翻一步碰撞初始算法中四节点Mindlin组合壳单元,对侧翻一步碰撞算法进行改进。以某12 m公路客车典型车身段作为研究对象,将改进算法模拟结果与初始算法、LS⁃DYNA及侧翻试验结果进行对比,检验了本文所提新型单元的实际中的有效性。
所提新型DKT组合薄壳单元,在厚向及各积分层积分方式和积分点数量对侧翻一步碰撞算法模拟精度及效率的影响尚未考虑,可能会对模拟结果有较大影响,在后续对此做进一步深入探讨研究,使侧翻一步碰撞算法性能得到进一步提升。
