不同输入方案对径流预测精度的影响研究

刘振男 周靖楠 陆之洋 徐桂弘

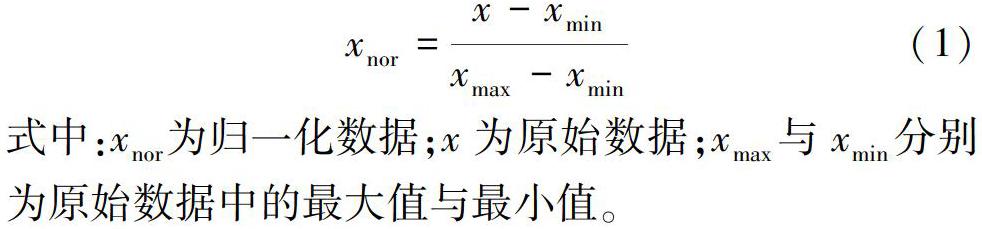
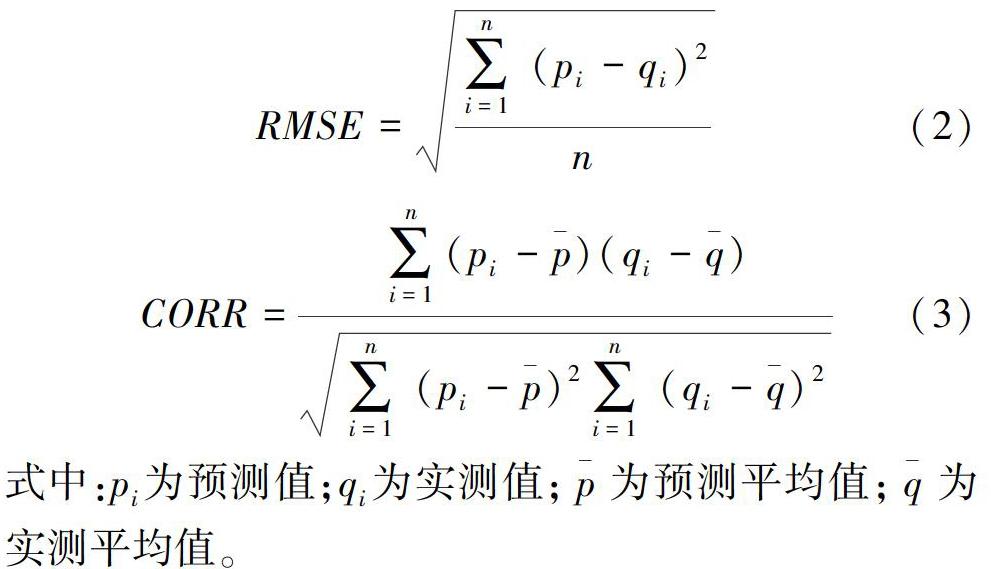
摘 要：径流预测对合理利用有限的水资源至关重要。基于成因分析法、主成分分析法（PCA法）、核主成分分析法（KPCA法）分别构建3种不同的模型输入方案，并采用自适应模糊推论系统（ANFIS模型）对河南省北汝河汝州水文站月径流量进行预测，依据均方根误差与相关系数对预测精度进行评价，从而明晰不同变量选择方法在径流预测当中的应用效果。结果表明：ANFIS模型适用于研究区的径流预测。PCA法、KPCA法分别构建的模型输入方案与成因分析法得到的方案相比，不但变量数目大幅减少，而且径流预测精度亦有大幅度的提高。与此同时，PCA法较KPCA法更适合重建研究区的径流预测变量方案。另外发现，模型运行时间与输入方案中的变量个数关系紧密，即变量个数越少，运行时间越短。

关键词：径流预测;主成分分析法;核主成分分析法;自适应模糊推论系统;预测因子

中图分类号：TP391.9 文献标志码：A

doi：10.3969/j.issn.1000-1379.2021.07.008

引用格式：刘振男，周靖楠，陆之洋，等.不同输入方案对径流预测精度的影响研究[J].人民黄河，2021，43（7）：41-44.

Abstract： Runoff prediction is very important for rational utilization of limited water resources. Based on the cause analysis method， PCA， KPCA and ANFIS model， the monthly runoff of RuzhouHydrology Station on the Beiru River in Henan Province was predicted. By means of root-mean-square error and correlation coefficient， the influence of different input schemes selected by different variable selection methods on runoff prediction accuracy was studied. The results show that the ANFIS model is suitable for runoff prediction in the study area. Compared with the schemes obtained by cause analysis， the input schemes constructed by PCA and KPCA respectively not only have a sharp decrease in the number of variables， but also greatly improve the accuracy of runoff prediction. Meanwhile， PCA is more suitable to reconstruct the runoff prediction variable scheme than that of KPCA. In addition， it is found that the running time of the model is closely related to the number of variables in the input scheme， that is， the smaller the number of variables， the shorter the running time.

Key words： runoff forecast; PCA; KPCA; ANFIS; forecasting factor

隨着我国经济快速发展，各行各业对水资源的需求量越来越大，因此合理有效地利用水资源至关重要，而径流的准确预测对于高效地分配有限的水资源具有重要的现实意义[1]。众所周知，大量不确定因素会对径流量的多少产生影响，给径流预测工作带来诸多挑战，如何有效地提高径流预测精度已成为水文预报研究领域的热点。传统的预测方法主要是根据河川径流自身存在的连续性、周期性等特点进行预测，如成因分析法、数理统计法以及时间序列法[2]。上述方法虽然能够较好地完成径流预测任务，但对资料质量要求较高且需要进行较为深入的物理成因分析，增加了径流预测的工作量。为了简化径流预测工作流程、提高预测精度，模糊数学法、混沌理论以及人工神经网络等方法被广泛应用[3]。实践证明，以上新兴方法不但能够提高径流预测精度，而且不用过多地进行物理成因分析，从而达到简化径流预测工作流程的目的。王佳等[4]基于集合经验模态分解法与人工神经网络法提出了一种新的预测模型（EEMD-ANN），并成功应用于黄河龙羊峡水库的月径流预测当中;张潇等[5]基于奇异谱分析和ARIMA模型对青弋江西河镇站月径流进行了预测，较单一的ARIMA模型精度有了大幅度提高;张敬平等[6]基于经验模态分解与径向基函数神经网络提出了一种预测模型，且完成了径流预测任务。综上可知，研究人员主要将精力集中在预测模型的改进工作中，往往忽略了客观存在的事实，即模型的输入方案亦会对预测精度产生显著影响。优选高效的变量作为模型输入，不但能够提升模型运行效率，而且对提高模型预测精度亦为关键。

目前，常用的模型输入变量筛选方法主要有以下两种：一是成因分析法，即借助气象学、水文学等理论知识，从径流形成的物理机制入手，深入研究相关气象、下垫面等因素对径流形成的直接作用，从而筛选出对径流具有显著影响的因素作为预测因子，该方法的优势在于能够给出径流量多少的合理解释，但其内在规律很难被完全揭示;二是数理统计法，即运用统计学等理论知识，基于数据挖掘理念，以相关分析等方法为手段，筛选与径流存在显著统计关系的因素作为预测因子。为了进一步简化模型输入方案、提高预测精度，在相关分析的基础上，主成分分析法能够有效地对预测变量进行降维，进而达到减少模型输入因子数量的目的，但是该方法主要是对原有预测变量进行线性降维，而径流与其影响因素间或多或少掺杂着非线性关系，显然需要一种能够处理非线性关系的降维方法，核主成分分析法就是典型代表方法之一。

主成分分析法与核主成分分析法在径流预测因子筛选中的应用研究还鲜有报道，因此有必要系统地展开相关研究。笔者以北汝河的水文数据为基础，基于自适应模糊推论系统，就主成分分析法与核主成分分析法选择的不同输入变量对径流（月均流量）预测精度的影响展开研究，既可以完成研究区的径流预测工作，又可以探明适用于研究区的径流预测输入变量选择方法，以期为当地的水资源合理规划提供参考。

1 研究方法

1.1 主成分分析法

主成分分析法（Principal Component Analysis，PCA）是一種数学降维方法，即将大量的具有一定线性相关性的变量重新组合，形成一组具有较少个数的互不相关的新变量并取代原有变量，详细原理可以参见文献[7]。具体计算步骤可简述如下：①计算原变量的相关系数矩阵;②求出相关系数矩阵的特征值以及相应的正交化单位特征向量;③选择主成分;④计算主成分得分;⑤确定最终新变量。

1.2 核主成分分析法

核主成分分析法（Kernel Principal Component Analysis，KPCA）是一种经典的多元统计方法，是在PCA的基础上改进而来的一种能够处理非线性关系的降维方法，其改进思想为将原有的多个变量通过核方法（非线性）映射到高维特征空间，从而在高维空间上进行主成分分析以达到数据降维的目的，最终确定能够取代原有变量的少数新变量，详细原理可以参见文献[8]。具体计算步骤可简述如下：①计算原变量的核矩阵;②执行核矩阵中心化操作;③计算核矩阵的特征值和特征向量;④数据重建;⑤确定最终新变量。

1.3 自适应模糊推论系统

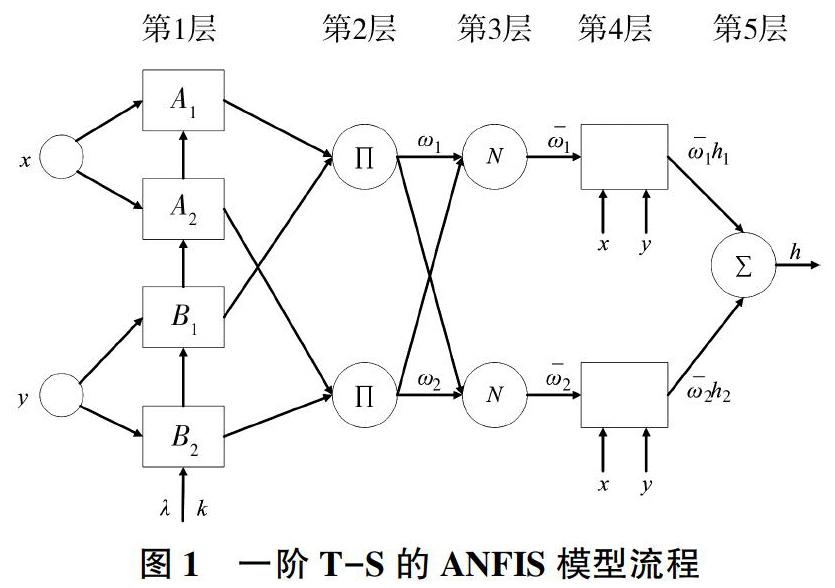
自适应模糊推论系统（Adaptive Network-Based Fuzzy Inference System，ANFIS）是由Jang于1993年提出来的一种耦合模型[9]，该模型集成了模糊逻辑与神经网络的优点，采用反向传播算法与最小二乘法对初始参数进行优化调整，从而自动产生If-Then规则。事实上，ANFIS是一种基于Takagi-Sugeno（T-S）模型的模糊推理系统，一阶T-S模糊推论系统的ANFIS模型流程如图1所示。其中：x与y为输入;A1、A2、B1、B2为模糊集合;λ与k为ANFIS的前件参数，是调整隶属度函数的关键参数;∏代表模糊规则;N代表归一化规则;w1与w2为模糊规则的可信度;1与2为可信度的归一化形式;h1 与h2为规则结论;h为最终输出。

显然，ANFIS是一个多层前馈网络模型。其中：第1层为输入的隶属函数层，第2层为规则的强度释放层，第3层为规则强度的归一化层，第4层为自适应节点层，第5层为计算输出层。

2 径流预测及影响分析

2.1 研究区概述

北汝河位于河南省境内，是颍河水系的主要支流，干流长约250 km，流域面积约5 670 km2。该流域属大陆性季风气候区，多年平均气温约14 ℃，多年平均水面蒸发量1 000 mm，多年平均降水量750 mm，春冬两季干燥少雨，夏季炎热多雨，降水时空分布不均，年际、年内变化较大，汛期降水约占总降水量的62%，受季风影响易出现特大暴雨。由于北汝河支流较多，干流上无控制性水利工程，流域洪水主要由暴雨导致，中上游河道坡度较大，汇流速度较快，易发生突发性洪涝灾害，因此对北汝河开展径流预测研究对当地防洪减灾工作具有重要的现实意义。

2.2 数据处理

研究所用资料为1985—2016年汝州水文站逐月降水量、土壤含水量、蒸发量以及径流量数据，数据来源可靠。由产汇流理论可知，径流量与前期降水量、土壤含水量以及蒸发量之间存在一定的物理成因关系，因此前期降水量、土壤含水量以及蒸发量对径流量的影响作用具有一定的滞后性。基于降水量、土壤含水量以及蒸发量，选用12个月为最大提前期，初步建立了含有36（12×3）个变量的径流预测待选因子集。预测待选因子具体描述如下：降水预测因子为P（t-i）（t代表时间），土壤含水量因子为S（t-i），蒸发量因子为E（t-i）。其中，i（i=1，2，…，12）表示提前期，例如P（t-1）代表提前一个月的降水量数据，其余的依此类推。

2.3 输入方案的确定

为了全方位比较不同方法确定的模型输入方案对预测精度产生的影响，基于成因分析法、PCA法与KPCA法设计了3种不同的模型输入方案。

（1）由成因分析法可知，含有36个待选预测变量的因子集中的每个因子均与径流存在一定的关系，因此第1种模型输入方案为待选预测因子集中的全部变量，即输入方案1含有36个变量。

（2）应用PCA法对变量进行降维之前需要对变量间的相关性进行分析。若变量间的相关性较强，则有必要运用PCA法对原有变量进行主成分提取;否则，不存在使用PCA法对原有变量进行降维的基础。为此，计算得到了36个待选变量间的相关系数矩阵，其表明，大多数变量间存在显著的线性相关性，除了自相关以外，正相关系数最大值为0.667 7，负相关系数最小值为-0.499 1。显然，可用PCA法对36个变量进行降维操作，故采用MATLAB软件编程对上述变量执行PCA操作，累计贡献率设置为0.9，最终形成含有7个变量的模型输入方案2。

（3）在36个变量的基础上直接运用KPCA法执行降维操作，同样借助MATLAB软件编程，累计贡献率同样设置为0.9，最终重组形成含有8个变量的模型输入方案3。

为了提高模型运行效率，对3种输入方案中的预测变量以及径流数据按照式（1）统一进行了归一化处理。

式（1）为正向变量（降水量、土壤含水量）的归一化公式，需补充反向变量（蒸发量）的归一化公式？

式中：xnor为归一化数据;x为原始数据;xmax与xmin分别为原始数据中的最大值与最小值。

通过上述归一化方法，可将原始数据控制在[-1，1]之间。模型计算后，再将输出结果进行反归一化处理，得到最终预测结果。

2.4 模型构建

根据ANFIS模型原理，应用MATLAB软件编程。其中，采用genfis3函数生成ANFIS的初始结构，模型迭代代数为300，隶属函数为高斯函数，其数目设置为10。模型训练期为1985—2012年，测试期为2013—2016年。预测效果的评价指标采用均方根误差（RMSE）和相关系数（CORR）。RMSE的值越接近0且CORR的值越接近1，说明预测精度越高。

式中：pi为预测值;qi为实测值;为预测平均值;为实测平均值。

考虑到模型运行的不稳定性，3种输入方案结合ANFIS分别运行10次，最终计算RMSE与CORR的平均值对径流预测精度进行评价。

2.5 结果分析

基于输入方案1～3，结合ANFIS模型对北汝河的径流情况进行预测，精度评价情况见表1。由表1可知，ANFIS模型具有良好的泛化能力，即模型训练期的评价指标RMSE与CORR优于测试期的，且ANFIS模型适用于研究区的径流预测，预测结果具有较高的可靠性。同时发现，模型运行时间与模型输入方案中变量数目有关，即输入方案中变量数目越大，模型運行时间越长。应用不同输入方案时，模型的运行时间从长到短的顺序为：方案1（36个变量）>方案3（8个变量）>方案2（7个变量）。预测精度由高到低的顺序为：方案2>方案3>方案1。

为了评价不同输入方案对预测模型运行稳定性的影响，采用箱线图进行评价，图中箱体越短表示预测模型运行的稳定性越高。ANFIS模型基于3种不同输入方案分别运行了10次，因此分别绘制了ANFIS模型基于不同输入方案运行结果的箱线图，如图2所示。整体上来看，RMSE表现出来的稳定性不及CORR。测试期，3种方案的稳定性能大体一致;训练期，由PCA法与KPCA法构建的方案2与方案3的运行稳定性明显优于未进行任何改进的方案1的运行稳定性。

为了直观地比较ANFIS模型结合不同输入方案所得预测结果的精度，图3给出了基于不同输入方案所得预测结果与实测值的对比。显然，ANFIS模型结合方案2与方案3所得的预测结果较结合方案1所得的预测结果更加接近实测值。

以上结果说明：由PCA法与KPCA法重建的模型输入方案不但能够有效提高径流预测精度，而且还有助于提高模型运行的稳定性。与此同时，由于原始预测变量间存在较为显著的线性相关关系，因此由PCA法重建的方案2的径流预测精度又高于由KPCA法重建的方案3的。

3 结 论

以北汝河水文数据为研究基础，基于PCA法与KPCA法重建了径流预测模型输入方案，结合预测模型ANFIS，分析了不同输入方案对径流预测精度产生的影响。结果表明：ANFIS模型适用于研究区的径流预测工作，由成因分析法、PCA法及KPCA法组建的3种模型输入方案均能得到较为满意的径流预测结果。其中，由PCA法与KPCA法组建的输入方案的预测精度较成因分析法组建的输入方案的预测精度有大幅度提高，模型运行时间也有了相应的缩短。与此同时，由于原始预测变量间存在较为显著的线性相关性，因此PCA法较KPCA法更适合重建研究区的径流预测因子。

参考文献：

[1] 张金萍，李红宾，肖宏林，等.基于误差修正模型的黄河源区年径流预测[J].人民黄河，2020，42（7）：5-8.

[2] 王文，马骏.若干水文预报方法综述[J].水利水电科技进展，2005，25（1）：56-60.

[3] 桑宇婷，赵雪花，祝雪萍，等.基于CEEMD-BP模型的汾河上游月径流预测[J].人民黄河，2019，41（8）：1-5.

[4] 王佳，王旭，王浩，等.基于EEMD与ANN混合方法的水库月径流预测[J].人民黄河，2019，41（5）：47-50.

[5] 张潇，夏自强，黄峰，等.基于SSA-ARIMA模型的青弋江干流径流预测[J].中国农村水利水电，2015（3）：6-9.

[6] 张敬平，黄强，赵雪花.经验模态分解和RBF网络在径流预测中的应用[J].干旱区资源与环境，2014（6）：118-123.

[7] WOLD S， ESBENSEN K， GELADI P. Principal Component Analysis[J].Chemometrics and Intelligent Laboratory Systems，1987，2（1-3）：37-52.

[8] SCHOLKOPF B， SMOLA A， MULLER K R. Kernel Principal Component Analysis[C]//International Conference on Artificial Neural Networks. Heidelberg， Berlin： Springer， 1997：583-588.

[9] JANG J S R. ANFIS： Adaptive-Network-Based Fuzzy Inference System[J].IEEE Transactions on Systems， Man， and Cybernetics，1993，23（3）：665-685.

【责任编辑 张 帅】