沁河年径流量非一致性水文频率分析

马钰其 陈元芳 张学成

摘 要：气候变化和人类活动加剧使得水文序列的一致性遭到破坏，在变化环境下传统频率分析方法不再适用。选择沁河下游武陟站1951—2016年共66 a实测年径流量数据为研究对象，使用Hurst系数法对年径流量序列进行初步诊断，再运用线性回归、Spearman秩次相关检验和Kendall秩次相关检验3种方法对序列进行趋势诊断，采用Bayesian变点分析、Pettitt检验等9种方法进行跳跃诊断，基于水文序列振动中心重构方法对变异序列进行一致性修正，再对修正后的序列进行水文频率分析。结果表明，武陟站年径流量序列的Hurst系数为0.84，属于强变异，于1964年发生向下跳跃变异;修正后序列的频率计算成果在不同设计标准下均小于原序列的，且差值随设计标准提高而增大。

关键词：非一致性;年径流量;变异诊断;频率计算;沁河流域

中图分类号：TV121 文献标志码：A

doi：10.3969/j.issn.1000-1379.2021.07.005

引用格式：马钰其，陈元芳，张学成.沁河年径流量非一致性水文频率分析[J].人民黄河，2021，43（7）：24-27，50.

Abstract： Climate change and intensified human activities have destroyed the consistency of hydrological series that make traditional frequency analysis methods no longer applicable under changing environment. The measured annual runoff data during 1951-2016 （66 years） at Wuzhi Station locatedon the lower reaches of the Qinhe River was selected as the research object. Preliminary diagnosis of series by Hurst exponent method， then using linear regression method， Spearman rank correlation test and Kendall rank correlation test to make trend detection， Bayesian variable point analysis and Pettitt test all together 9 kinds of method to do change point test. It corrected the non-stationary series by vibration center reconstruct technology and analyzed the modified series. The diagnostic results show that the Hurst exponent of the annual runoff series at Wuzhi Station is 0.84， showing a strong variability. Downward jump variation shows in 1964. The frequency calculation results of the modified series are smaller than that the original series under different design standards and the difference increases with the design standard improvement.

Key words： non-stationary; annual runoff; variation diagnosis; hydrological frequency analysis; Qinhe River basin

年径流量频率分析的主要任务是研究其时空分布规律，为水利工程规划设计、水资源合理开发利用提供依据[1]。在气候变化和人类活动加剧的背景下，水文序列的一致性假设受到挑战，传统频率计算方法所得结果的可靠性受到质疑。因此，探讨非一致性水文序列频率分析方法具有重要的理论意义和应用价值。

近年来，国内外学者对这一问题进行了深入研究，取得了丰硕的成果[2-3]。目前非一致性水文频率分析方法分为两大类：一是数理统计方法，直接对非一致性水文序列进行频率计算;二是基于水文极值序列重构途径，对非一致性水文序列进行重构，使重构后的序列满足一致性要求，再利用传统方法进行水文频率计算。直接计算的常用方法有混合分布法[4]、条件概率分布法[5]和时变矩法[6-8]，前两种方法多用于具有跳跃变异的水文序列，而时变矩法主要应用于具有趋势性变异的水文序列。混合分布法认为，受暴雨、冰雪融水等因素影响，水文极值序列并不满足同分布假定，且通常由两种或两种以上的混合分布组成。瞿宁玲等[9]以米市渡站年最低潮位为研究对象，假定序列变异点前后序列分别服从2个P-Ⅲ型分布，采用模拟退火算法估计参数，结果表明基于混合分布得到的新序列理论频率与经验分布拟合较好。条件概率分布法假定不同时段内样本相互独立且服从不同分布，同一时段内样本则服从同一分布，极值序列以不同的条件概率发生在不同时段，通过全概率公式即可推求极值出现在任意时段内的概率。宋松柏等[10]用全概率公式推导了非一致性水文序列頻率计算公式，公式可以灵活选择频率分布组成，且适用于有多个变异点的水文序列。时变矩法的主要思想是建立水文序列所服从分布函数的统计参数与协变量之间的关系，以协变量的变化驱动分布函数中统计参数的变化，从而确定未来某一状态下序列的分布函数，该方法直接考虑统计参数的非一致性，这也导致其在某一频率下的设计值随协变量变化而变化，无法直接用于水文频率分析。

水文极值序列重构途径的核心是重构方法的选择，目前常用的方法有3种：一是水文模拟法，建立不同时期下垫面条件与水文模型参数之间的统计关系，通过水文模型模拟计算实现序列的重构，如韩瑞光等[11]应用雨洪模型模拟了阜平站以上山区1980—1989年的典型洪水，实现了洪水序列的一致性修正;二是谢平等[12]提出的时间序列分解合成法，该方法假设水文序列由非一致的确定性成分和相对一致的随机性成分组成，应用时，首先对序列进行变异诊断和成分识别，再对确定性成分进行拟合计算和对随机性成分进行频率计算，最后将确定性的预测值和随机性的设计值进行合成，得到不同時期合成序列的频率分布;三是参数关系分析法，该方法常用降雨量作为参数建立变异点前后序列的降雨径流关系，以此实现变异点前后径流序列的重构，如陆中央[13]运用该方法，实现了河北省山区和平原地区年径流序列的“向后还原”。

笔者以沁河武陟站年径流量序列为分析对象，对序列进行初步诊断、详细诊断，应用无未来信息的振动中心重构方法对变异序列进行一致性修正，简要概括原序列和修正后序列的统计参数及不同重现期对应设计值的变化规律，为沁河年径流量分析计算提供技术支撑和思路参考。

1 研究区概况及数据

1.1 研究区概况

沁河是黄河一级支流，发源于山西省沁源县太岳山区东部，自北向南流经山西、河南两省，于武陟县城南方陵村注入黄河，全长485.1 km，流域面积13 532 km2。沁河流域介于北纬34°54′—36°59′、东经111°56′—113°49′之间，其最大支流为丹河。

1.2 研究数据

研究数据采用水利部黄河水利委员会水文局提供的沁河武陟站1951—2016年（共66 a）实测年径流量数据。需要说明的是武陟站旧称木栾站、小董站，于1969年更名为武陟站并沿用至今。

2 研究方法

2.1 水文序列变异诊断

水文序列的变异诊断是非一致性条件下年径流量频率分析的首要工作。本文首先使用Hurst系数法[14]对年径流量序列进行初诊，根据Hurst系数值确定序列的变异程度;然后运用线性回归法、Spearman秩次相关检验和Kendall秩次相关检验法进行趋势诊断;最后采用Bayesian变点分析法、Pettitt检验法等9种方法进行跳跃诊断，综合各种检验结果，得出序列的变化趋势和可能变异点。

2.2 非一致性水文频率计算

目前，我国水文序列的样本长度通常不超过70 a，样本序列呈现的变异性可能仅是“总体”的周期性特征，在小样本且无未来信息的条件下进行参数估计和频率适线，其结果均存在较大的不确定性。针对这一情况，胡义明等[15]认为“发生跳跃变异的序列存在着某种理想化的平稳状态，且这种平稳状态的振动中心（均值）是序列变异点前后两实测样本均值的线性组合”。基于这一假定，结合序列诊断结果可对非一致性序列进行重构。

应用式（3）对方差较大的序列进行修正时，原序列的极小值重构后可能会出现负值，显然有违客观事实。笔者在此提供如下仍基于原假设的异常值处理思路。

假设重构后异常值出现在变异点前的序列，且变异点后的序列重构后无异常值，即

yi<0（1≤i≤τ），则对重构序列中小于零的样本值按照绝对值从大到小排序，再对变异点后重构后序列按照数值从小到大排序，最后使用变异点后重构序列的最小值依次代替异常值即可。若异常值序列长度超过重构后不存在异常值序列总长，则说明原序列可能存在多个变异点（振动中心），应当重新对序列进行变异诊断，选择其他方法进行水文频率分析。

该方法是“振动中心是序列变异点前后两实测样本均值的线性组合”这一假设的理论延伸，假定重构后序列整体处于振动中心水平，具备使用无异常值序列的最小值代替异常值的理论基础。

根据之前的研究成果，P-Ⅲ型分布对我国年径流资料适应性较好[16]，线性矩法估计参数的稳定性较强[17-18]，故本文选用P-Ⅲ型分布确定不同保证率下年径流量的设计值。

3 结果分析

3.1 年径流量序列非一致性诊断结果

综合各种诊断方法的结果，可得出如下结论：武陟站年径流量呈显著递减趋势，且于1964年发生跳跃变异。查地方志和相关资料了解到，沁河下游广利灌区1958年后兴建平原水库17座。支流丹河上丹东、丹西两灌区于1960年开始引水灌溉，直接导致丹河入沁水量减少。推测是以上原因造成武陟站年径流量减少，发生向下跳跃变异，佐证了诊断结果。详细变异诊断结果见表1，年径流量变化情况如图1所示。

3.2 年径流量序列的一致性修正及频率分析

以发生跳跃变异的1964年为振动中心，按照上文介绍的振动中心重构法对武陟站实测年径流量序列进行一致性修正，再采用Mann-Kendall检验法对重构后的新序列进行趋势检验，结果表明，在0.05显著性水平下修正后序列无显著趋势，满足一致性假定，可以用于年径流量频率分析。修正后序列的检验结果见图2。

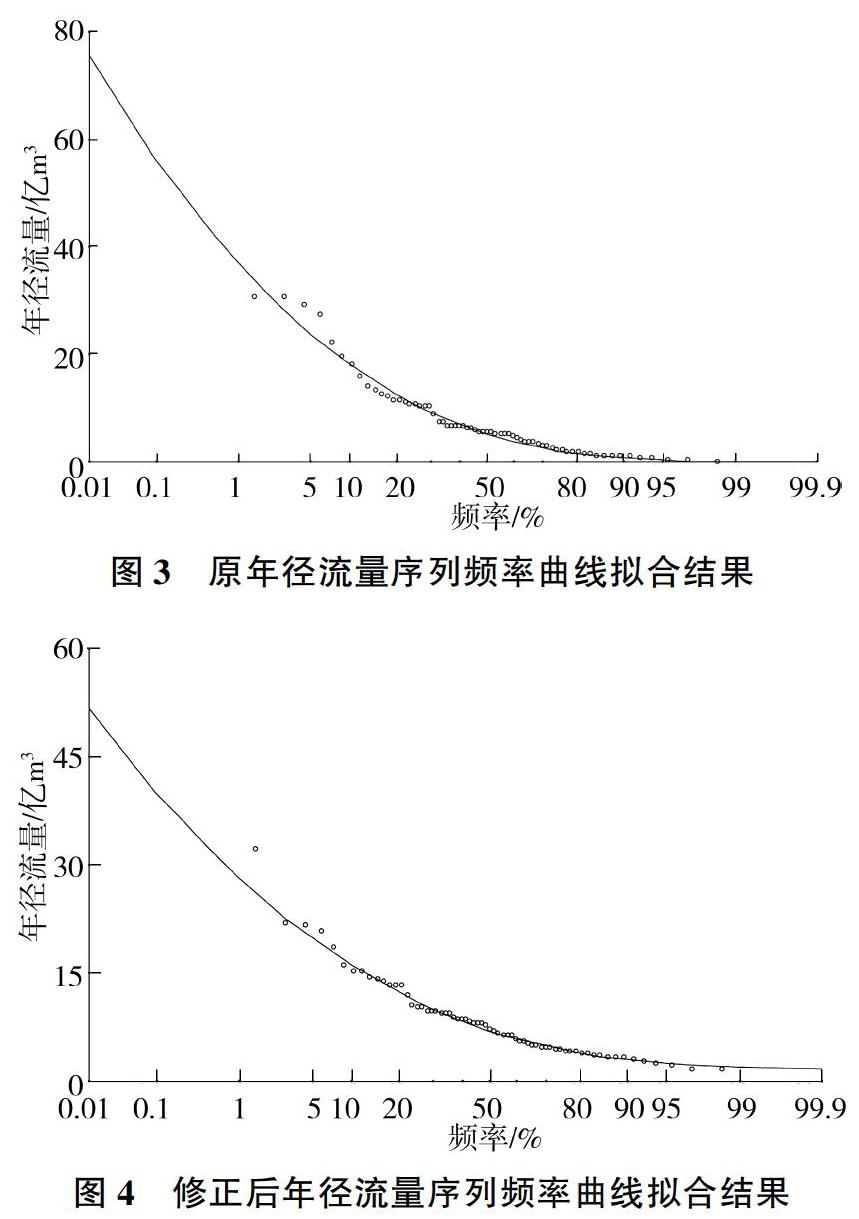
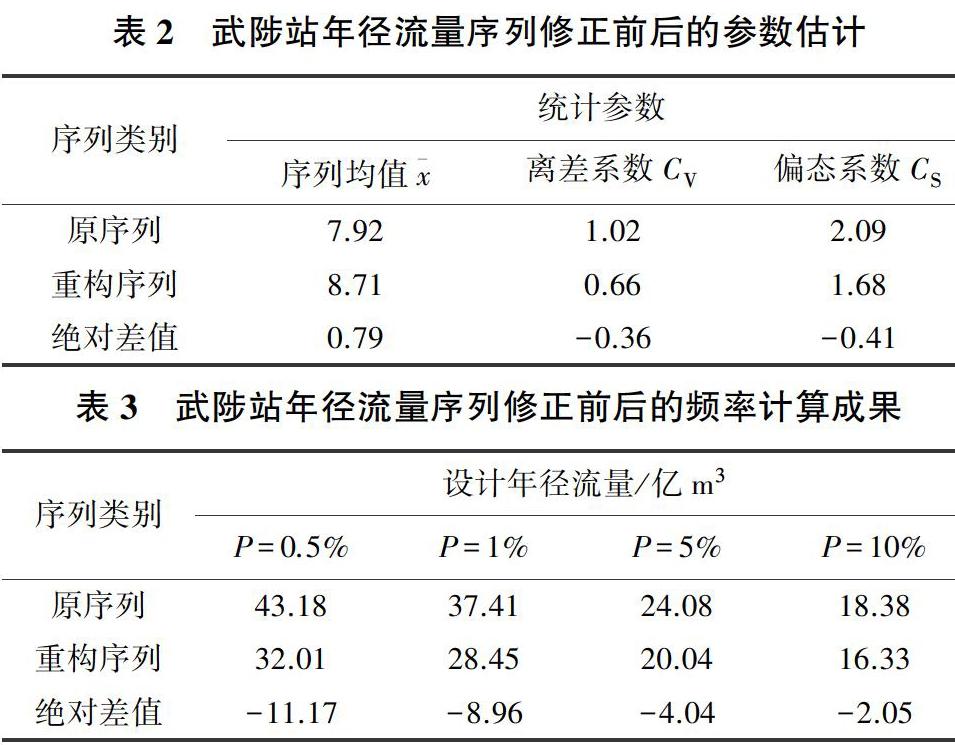
对原序列和经过振动中心重构后满足一致性假设的新序列分别进行水文频率计算，原则上未经修正的原序列不满足一致性假设，无法使用传统方法进行频率分析，其计算结果在此仅起对照作用，以提醒规划设计人员在实践中要先对序列进行诊断，再根据诊断结果选择合理的分析方法。频率曲线选择P-Ⅲ型，通过线性矩法估计参数，并结合目估适线法对结果进行微调。原序列及一致性修正后序列的经验频率曲线拟合结果如图3、图4所示，实测序列与重构修正序列的参数估计结果及不同频率对应的设计值见表2、表3。

由表2中数据可知，统计参数方面，经一致性修正后的序列较原序列均值增大了0.79，而离差系数CV和偏态系数CS均小于原序列的;从参数的变化幅度上看，离差系数变化幅度高达35.29%，而均值变化幅度仅9.97%，修正后序列的离散程度较原序列明显减小，与经验频率曲线拟合结果相吻合。从年径流量设计值上看，表3中设计频率标准越低，则设计值的差异幅度越小，重构序列在设计频率P=10%、5%情况下的设计值较不考虑非一致性的原序列设计值分别减小了11.15%和16.78%，当设计标准提高到100 a一遇和200 a一遇时，设计年径流量的相对差值高达23.95%和25.87%。结合沁河年径流量呈下降趋势的事实，若不考虑序列的变异与修正直接进行频率计算，将增大工程规模，造成巨大的资源浪费，导致严重的后果。

4 结 论

（1）采用Hurst系数法等3种趋势诊断法、Bayesian变点分析法等9种跳跃诊断法共13种方法对武陟站1951—2016年（共66 a）实测年径流量序列进行变异诊断。结果表明，序列变异程度属强变异，年径流量呈减少趋势，综合多种方法得到的检验结果与水文调查成果，最终确定在1964年发生显著向下跳跃变异，变异原因是干、支流灌区过量引水和修筑水利工程。

（2）原序列和修正后序列的频率计算成果存在显著差异。统计参数方面，修正后序列均值較原序列均值增大了0.79，而离差系数和偏态系数分别减小了0.36和0.41;修正后序列不同重现期的设计值均小于原序列设计值，绝对差值和相对差值均随设计标准提高而增大，结合趋势诊断结果，经一致性修正后的序列计算得到的设计值更符合沁河当前的水文情势。

（3）武陟站是沁河入黄把口站，分析其年径流量变化趋势对进一步研究沁河入黄水量变化及流域水利工程规划设计都有非常重要的意义。结合本文研究成果，后续相关研究应充分考虑气候变化和人类活动影响，对实测序列进行变异诊断，再根据诊断结果选择合理的分析计算方法，以期得到更为合理可靠的结论。

（4）如何处理无未来信息条件下水文序列振动中心重构法得到的异常值还有待进一步研究。本文推荐的方法仅是原假设的理论延伸，在频率计算方面有原序列计算成果作对照，有充足的理论依据。

参考文献：

[1] 詹道江，徐向阳，陈元芳.工程水文学[M].4版.北京：中国水利水电出版社，2010：168-169.

[2] 梁忠民，胡义明，王军.非一致性水文频率分析的研究进展[J].水科学进展，2011，22（6）：864-871.

[3] 胡义明，梁忠民，姚轶，等.变化环境下水文设计值计算方法研究综述[J].水利水电科技进展，2018，38（4）：89-94.

[4] SINGH K P， SINCLAIR R A. Two-Distribution Method for Flood Frequency Analysis[J].Journal of the Hydraulics Division，1972，98（1）：28-44.

[5] SINGH V P， WANG S X， ZHANG L. Frequency Analysis of Nonidentically Distributed Hydrologic Flood Data[J].Journal of Hydrology，2005，307：175-195.

[6] STRUPCZEWSKI W G， KACZMAREK Z. Non-Stationary Approach to At-Site Flood Frequency Modelling II. Weighted Least Squares Estimation[J].Journal of Hydrology，2001，248（1-4）：143-151.

[7] STRUPCZEWSKI W G， SINGH V P， FELUCH W. Non-Stationary Approach to At-Site Flood Frequency Modelling I. Maximum Likelihood Estimation[J].Journal of Hydrology，2001，248（1-4）：123-142.

[8] STRUPCZEWSKI W G， SINGH V P， MITOSEK H T. Non-Stationary Approach to At-Site Flood Frequency Modelling II. Flood Analysis of Polish Rivers[J].Journal of Hydrology，2001，248（1-4）：152-167.

[9] 瞿宁玲，王安琪，陈元芳，等.米市渡站最低潮位的非一致性频率分析[J].水电能源科学，2018，36（10）：34-38.

[10] 宋松柏，李扬，蔡明科.具有跳跃变异的非一致分布水文序列频率计算方法[J].水利学报，2012，43（6）：734-739，748.

[11] 韩瑞光，冯平.流域下垫面变化对洪水径流影响的研究[J].干旱区资源与环境，2010，24（8）：27-30.

[12] 谢平，陈广才，夏军.变化环境下非一致性年径流序列的水文频率计算原理[J].武汉大学学报（工学版），2005，38（6）：6-9，15.

[13] 陆中央.关于年径流量系列的还原计算问题[J].水文，2000，20（6）：9-12.

[14] 谢平，陈广才，雷红富.基于Hurst系数的水文变异分析方法[J].应用基础与工程科学学报，2009，17（1）：32-39.

[15] 胡义明，梁忠民，赵卫民，等.基于跳跃性诊断的非一致性水文频率分析[J].人民黄河，2014，36（6）：51-53，57.

[16] 丘宁，陈喜，高满.中国年径流频率分布及统计特征区域规律分析[J].水电能源科学，2015，33（12）：1-5.

[17] 陈元芳，沙志贵，陈剑池，等.具有历史洪水时P-Ⅲ分布线性矩法的研究[J].河海大学学报（自然科学版），2001，29（4）：76-80.

[18] 雷冠军，王文川，殷峻暹，等.P-Ⅲ型曲线参数估计方法研究综述[J].人民黄河，2017，39（10）：1-7.

【责任编辑 张 帅】