PCA-GA-LM模型在水库土石坝渗流预测中的应用

缪新颖，单玉鹏，纪建伟

（1. 大连海洋大学a.信息工程学院, b.食品科学与工程学院,辽宁大连116023；2. 沈阳农业大学 信息与电气工程学院,沈阳110161）

水库大坝的安全直接关系到水库的正常使用和下游农田及农村的安全[1]。在中国现存的大坝中,土石坝居多,而在影响土石坝安全的因素中,渗流占有很大的比例[2]。因此，及时分析渗流监测数据和做出可靠的水库大坝安全预测非常重要[3]。一些统计模型[4]被用于安全评价分析和预测,在一定程度上可以揭示水库大坝效应变量与其影响因素之间的定量关系[5],然而数学模型通常是基于一些假设,如:观测值之间相互独立的,误差满足正态分布,误差的数学期望值是0等[6-7]。此外,数学模型的输入量选择不当,模型的准确性将受到很大影响[7]。

神经网络作为一种非线性优化工具[8-9],适应水库大坝渗流及其影响因素之间的非线性关系,已被许多研究者采用[10-15]。然而,传统的BP(back propagation)神经网络在收敛速度[16-18]和泛化能力[19-22]等方面存在缺陷,而且大多数神经网络结构是通过试凑法[23]确定的,耗时较长[24]。此外,神经网络影响因素确定的准确与否对预测结果至关重要[24]。Levenberg marquardt (LM)算法[25]采用Gauss-Newton 法搜索最优值,下降速度快[26],通过自适应调整网络权值,使每次迭代不再沿单一的负梯度方向进行,从而大大提高网络的收敛速度和泛化能力[5,7]。遗传算法(genetic algorithm, GA)[27]是受达尔文进化论的启发,利用编码串种群表示参数,基于一定的适应度函数,由遗传算子选择个体,通过连续的迭代与进化不断提高新种群个体的适应度,直到满足预设条件停止进化,并将适应度最高的个体作为待优化参数的最优解[7]。与传统的结构优化算法和试凑法相比,GA 通常能够快速地得到较好的优化结果,因此被用来优化神经网络[24,28-30]。

对于水库大坝的安全监测,影响水库大坝渗流的因素不止一个[31]。这些水库大坝影响因素的确定通常依赖于经验[7],项目组利用试验方法来确定水库大坝渗流的影响因素[24],证明了并非影响因素越多,预测效果越好,主要是因为影响因素之间存在着信息重叠,从而导致复杂性升高[24]。主成分分析(principal component analysis,PCA)是PEARSON[32]在1901年提出的,通过提取正交的主成分避免多重共线性,从而准确提高参数估计。此外，可以降低包含许多变量的数据集的维数,从而尽可能减少变量以包含尽可能多的信息,这可以使模型更有效[33-35]。

本研究提出了一种预测水库土石坝渗流的PCA-GA-LM 模型。采用PCA 确定影响因素,实现影响因素的去耦和降维,在此基础上,结合GA-LM 建立了水库土石坝渗流预测模型,并将算法与未用PCA算法的GA-LM 进行比较，以期为水库土石坝渗流预测提供参考。

1 基于PCA-GA-LM的水库土石坝渗流预测模型

1.1 水库土石坝渗流的影响因素分析

综合学者们的研究结果,土石坝的渗流特性可以通过测压管水位反映出来,并受到水库水位、降雨、温度、老化等多种因素的影响[7]。为了找到相对合适的渗流影响因素,项目组利用试验法对表1中渗流的3种影响因素方案进行GA-LM 预测比较,发现模型1的方案虽然不是影响因素最多,但却是预测精度相对最高[7],说明如何确定土石坝渗流的影响因素没有必然的规律,究其原因是影响因素之间存在着耦合性,相互影响,因此有必要寻找一种更科学有效的方式来确定渗流的影响因素。表1 中,H是水库水位,R是降雨量,T是温度,θ是时效因子。H0,H5,H10,H20和H30分别表示观测前0,5,10,20,30d 的平均库水位；同理,R和T也包含了5 个平均降雨量和温度；时效分量包括θ和lnθ,θ为从观测起始日期算起的天数的1%。

表1 渗流影响因素试验方案Table 1 Testing scheme of influence factors of the seepage

1.2 PCA-GA-LM模型的建立

本研究数据取自辽宁抚顺浑河上的大伙房水库,主坝坝型为黏土心墙土坝,最大坝高49.2m,坝顶长度1366.7m,控制流域面积5437km2,涉及农田灌溉面积8.6万hm2,是保障沈抚大地灌溉的重要水利工程。以大伙房水库某关键断面“pie3140”测压管观测数据为研究对象,利用2018 年的365 组数据作为训练样本,选取2019 年15组数据作为测试样本对渗流进行预测。在用GA-LM进化神经网络进行预测之前,先采用主成分分析法对影响因子进行解耦和降维。流程图见图1。

图1 PCA-GA-LM土石坝渗流预测模型流程图Figure 1 Flowchart of PCA-GA-LM prediction model of seepage of the earth-rockfill dam

1.2.1 水库土石坝渗流影响因子的确定 考虑到水库土石坝渗流影响因素之间的多重共线性和数量众多,利用主成分分析方法确定影响因子,从而实现去耦和降维。具体步骤如下。

步骤1：为了不丢失影响因素信息,选取表1 中的模型3 影响因素方案作为主成分分析的输入。由于17 个影响因素的维数大多不同,且数值变化很大,因此在测量影响因素的变化程度时,结果容易失真,偏向于大范围的影响因素。为了消除不同均值和方差对变量比较的影响,利用式（1）对17个影响因素的数据进行归一化。

式中：mean(X i)为平均值；σ(Xi)为标准差。

步骤2：利用式（2）求样本的协方差矩阵。

步骤3：计算样本协方差矩阵Cx的特征值λi及相应特征向量μi,其中i=1,2,…,p。

步骤4：特征值按降序排列,前m（m＜p）个主元的累积贡献率计算公式为：

此处将累积贡献率大于95%的前m个新生成分量作为主元。

步骤5：将前m个主元所对应的特征向量选出来,利用式（4）构建变换矩阵T,并利用式（5）计算出前m个主成分。

1.2.2 预测水库土石坝渗流 将体现渗流的水库土石坝测压管水位作为输出,将1.2.1中所确定的主成分作为输入,利用GA-LM模型预测水库土石坝渗流。具体的GA-LM算法如下。

（1）初始种群和编码。结构基因采用二进制编码,表示隐层节点结构（“1”表示存在隐层节点,“0”则表示不存在）；连接权值和阈值用权重基因表示,利用实数进行编码。当有n个隐层节点、x个输入、y个输出时,染色体结构见图2。

图2 染色体结构Figure 2 Construction of chromosomes

本研究选取种群大小为100,初始n=36。

（2）在式（6）求取误差平方和的基础上,按照式（7）进行适应度评价。

式中：V为经LM神经网络训练得到的输出值；T为V所对应的实际测量值；E为误差平方和（SSE）。

式中：F为适应度函数。通过向F高的方向进化,使误差逐步减小, 结构逐步趋于简单[7]。

（3）确定终止进化条件。以进化代数是否满足100代或均方误差MSE是否小于0.001为准则终止进化。

（4）遗传算子。选择算子采用轮盘赌策略；交叉和变异算子均根据染色体编码形式采用混合策略[6]。其中结构基因采用单点交叉和基本位变异算子；权重基因采用算术交叉和非均匀变异算子。初始交叉率和变异率分别为0.6和0.08。

（5）在LM算法中,权值的调整算法为：

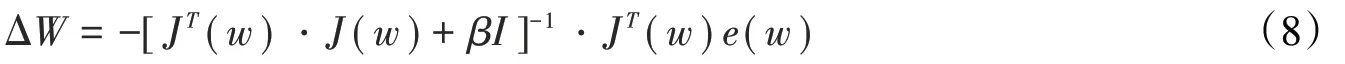
式中：J(ω)为Jacobian 矩阵；β为大于零的调整因子,用于控制LM 算法迭代；I为单位矩阵。本研究β的初始值设为0.01。

2 预测结果与分析

按照1.2.1 算法,对365 组数据归一化后的水库土石坝渗流部分数据见表2。由表2 可知，经过归一化的数值变化明显变小,可以消除不同均值和方差对变量比较的影响。

表2 归一化土石坝渗流影响因素Table 2 Normalized influence factors of the earth-rockfill dam seepage

对应的水库土石坝样本的协方差矩阵见表3。由表3 可知,17 个影响因素之间有一定的相关性,存在着较高的耦合,需要去耦。

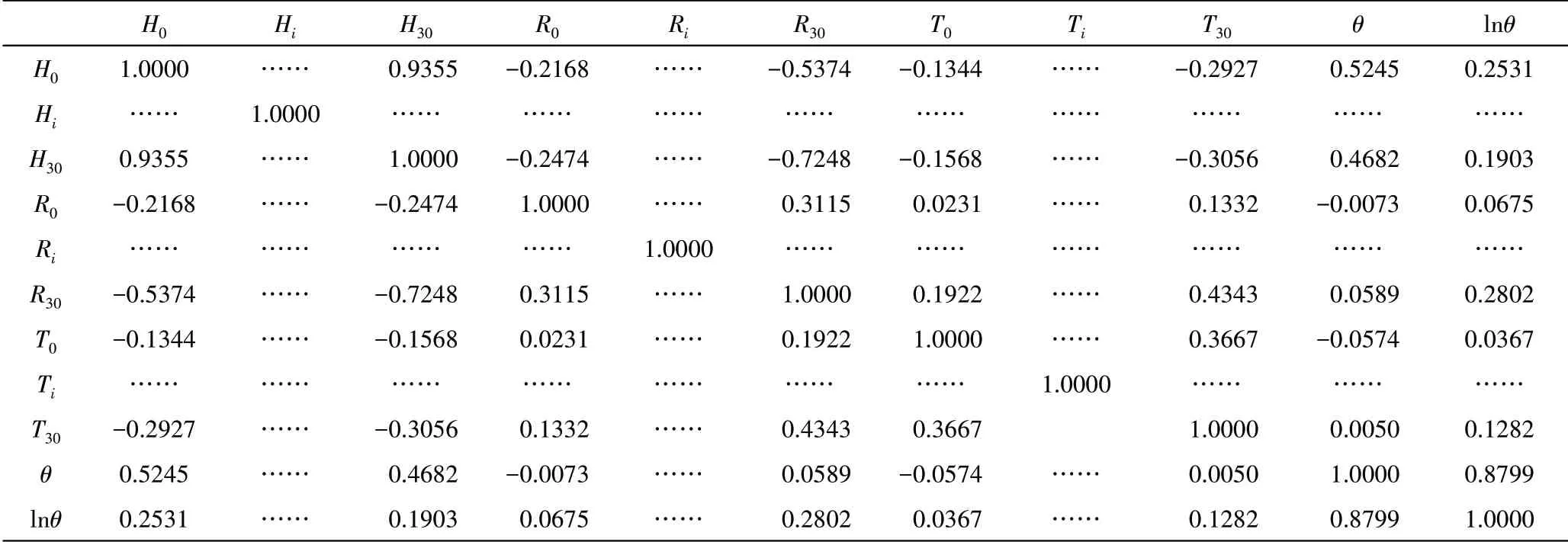
表3 土石坝样本的协方差矩阵Table 3 Covariance matrix of the earth-rockfill dam samples

计算出来的降序特征值和贡献率见表4。由表4可知,前8个主元的累计贡献率大于95%,且特征值较大,因此选取主成分数为8,按照式（4）和式（5）,对应的主成分表达式如式（9）。

表4 降序特征值和贡献率Table 4 Eigenvalue in descending order and corresponding contribution rates

在此基础上,利用1.2.2的GA-LM算法,得到的PCA-GA-LM 预测网络结构如图3,并据此完成测压管水位的预测。为了验证PCA-GA-LM 算法的预测效果,将采用PCA 方法的GA-LM 预测模型与表1中的3个GA-LM预测模型进行比较,比较结果见图4。可以看出,在4种模型中,PCA-GA-LM 模型的测压管水位预测值与测压管水位实测值拟合效果最好,吻合程度最高。由具体误差分析（表5）可知,PCA-GA-LM 模型的影响因子个数最少,平均误差、标准偏差和平均相对误差最小,预测准确率最高,能达到99.98%。采用试验法所确定的3 个模型中,模型2和模型3的影响因子数与PCA方法所确定的影响因子数相差较大,准确率也相差较多；模型1的影响因子数接近于PCA 方法,预测准确率与PCA 方法最为接近,说明模型1确定的影响因子有效性恰好接近PCA 方法,但该方法受试验法本身特点所限,确定过程带有很大的随机性。综合4种模型误差分析结果可知,本研究所提出的PCA-GA-LM 水库土石坝渗流预测模型是可靠的。

图3 PCA-GA-LM土石坝渗流预测网络结构Figure 3 Structure of PCA-GA-LM network for predicting seepage of the earth-rockfill dam

图4 基于PCA-GA-LM所预测的测压管水位与表1模型的比较Figure 4 Comparison of the predicted piezometric levels between PCA-GA-LM model and models in table 1

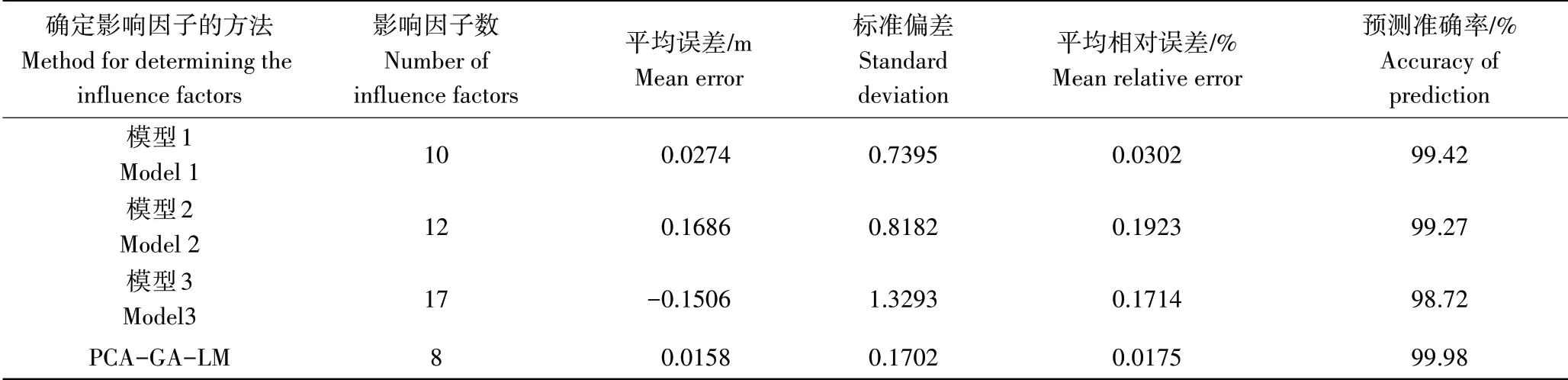
表5 基于PCA-GA-LM的测压管水位预测模型与表1模型的误差分析比较Table 5 Comparison of the dam prediction performance of the piezometric levels under the condition of PCA and without PCA

3 讨论与结论

对大坝重要效应量进行精准预测和确保大坝安全是使水库正常发挥蓄水功能、保障农业生产用水需求的重要举措。由此,研究准确率高、可操作性强的大坝渗流预测方法,例如本研究设计的方法,取代随机性的试验法,在有效影响因子确定、网络结构优化和预测算法3方面均有可操行性强的算法,且实际应用预测准确率高于其他文献方法,可以实现对大坝渗流的精准预测。

本研究在对土石坝渗流影响因素分析基础上,将PCA 算法与GA-LM 算法相结合,提出了一种用于水库大坝渗流预测的PCA-GA-LM 模型。作为一种有效的搜索方法,遗传算法被用来优化网络结构。针对传统BP 算法收敛速度慢、易陷入局部最优的缺点,采用了LM 算法进行渗流预测。为了确定合适的影响因子,使模型更加有效,采用PCA 确定水库土石坝坝体渗流的影响因素。从大伙房水库土石坝的应用实例可以看出,采用该模型预测的水库土石坝测压管水位值和实测值吻合度较高。采用PCA 和试验法情况下的水库土石坝渗流预测误差比较分析表明，采用PCA 的模型预测误差最小,可以获得更高的预测准确率。由此可见,本研究所建立的模型可以作为水库土石坝渗流预测的一种有效工具。