风力机尾缘襟翼气动特性及减振性能研究

何科杉，陈 严，漆良文，周 奇,2

(1.汕头大学 工学院，广东 汕头 515063；2.广东省高等学校结构与风洞重点实验室，广东 汕头 515063；3.汕头职业技术学院 机电工程系，广东 汕头 515078)

为了充分利用风力资源和降低风力发电度电成本，风力机大型化已成为必然的发展趋势。风力机叶片属于阻尼小、质量大、对风脉动敏感的高柔性结构，风荷载往往成为其结构设计需要考虑主要的荷载之一[1]。随着风力机叶片尺寸增大，质量增加，柔性增大，作用在叶片上的风荷载将更加复杂多变，且风荷载分布的不均匀程度增强，风致振动问题将更加突出。由风剪切、塔影效应、湍流等因素引起的风力机叶片疲劳荷载及结构振动，容易造成叶片的疲劳损坏甚至断裂破坏，从而影响风力机的安全性和可靠性[2]。通过有效的控制方法减少风力机叶片上的风荷载及结构振动，可有效提高叶片及整机的安全可靠性，从而降低风力发电的度电成本。目前风力机独立变桨距控制是较成熟的叶片气动及振动控制技术。叶片变桨距控制通过叶片整体转动改变攻角从而调节气动性能，具有调节能力强和调节范围大的特点。但随着叶片尺寸增大，其局限性越来越明显，主要体现在叶片质量增加，惯性增大，响应速度变慢，对高频的风荷载及局部荷载难以施加有效控制等。针对独立变桨距控制的不足，以尾缘襟翼控制为代表的风力机“智能叶片”技术被认为是最具发展潜力的有效补充方案[3]。风力机尾缘襟翼控制方案是在叶片尾缘处布置分布式襟翼，通过尾缘襟翼偏转改变叶片气动外型从而调节气动性能。尾缘襟翼控制具有转动惯性小，响应速度快，对高频荷载敏感，局部荷载可调节等特点，可有效补偿独立变桨距控制的不足，近年来得到了广泛的研究。

Bergami等[4-6]采用自适应柔性尾缘襟翼对风力机叶片进行降载减振控制，结果表明尾缘襟翼可有效调节叶片的气动性能，降低叶片的疲劳荷载，减少叶片的结构振动。Barlas等[7]采用分布式尾缘襟翼对风力机叶片进行降载减振控制，结果表明尾缘襟翼可有效降低叶片的疲劳荷载，且对风荷载的高频部分有较好的调节作用。Zhang等[8-10]研究多种湍流工况下尾缘襟翼对叶片的气动调节作用，结果表明在尾缘襟翼在多种湍流工况下对叶片都距有较好的降载减振作用。穆安乐等[11]研究分布式尾缘襟翼的预测控制方法，表明尾缘襟翼控制方法对气动调节效果有较大的影响。季康等[12-14]研究风力机尾缘襟翼的非定常气动特性，建立了尾缘襟翼的非定常气动模型，得到尾缘襟翼在多种工况下的非定常气动变化规律。

上述研究主要关注风力机尾缘襟翼的气动调节效果，对尾缘襟翼的气动调节作用机理的研究不够深入；尾缘襟翼的气动性能研究以模拟仿真为主，风洞试验研究较少；且尾缘襟翼与独立变桨距协同控制的研究也鲜见报道。因此，本文拟通过风洞试验研究尾缘襟翼的气动特性，探明尾缘襟翼对翼型绕流的作用机理；并通过风力机整机模拟仿真，研究独立变桨距与尾缘襟翼协同控制对风力机叶片的降载减振作用效果，为风力机尾缘襟翼的研究应用提供参考依据。

1 风力机尾缘襟翼气动特性试验

1.1 风洞试验方案

风力机尾缘襟翼风洞测压试验在汕头大学大气边界层风洞的主测试段完成。该风洞主测试段尺寸为3 m×2 m×20 m，通过可调节顶板以保证来流方向的零压力梯度，风速连续可调，最高风速可达45 m/s。测压试验数据通过DSM3200电子扫描阀测压系统采集，测压模块为ZOC33，风速测量采用TFI Cobra探头，试验模型测压参考高度上的总压和静压与试验模型表面测压孔的风压数据同步采集。

风力机尾缘襟翼试验模型为一个两端等宽的翼型段，弦长为600 mm，展长为600 mm；叶片尾缘部分(占弦长10%)为可转动的尾缘襟翼。尾缘襟翼通过两端的连接板与叶片本体连接，并通过转轴与西格玛 OSMS-40YAW微型自动转动平台连接。通过控制自动转台转动，可带动尾缘襟翼偏转±20°。试验模型采用NACA 64618翼型，该翼型是美国可再生能源实验室设计的NREL-5MW参考风力机叶片的主要翼型之一。为保证试验模型刚度足够大和质量足够小，叶片本体部分采用铝制框架作为骨架，内部采用XPS挤塑板(豪适板)加工定型，并在模型外层采用碳纤维布蒙皮，喷涂油漆以保证表面光洁度。尾缘襟翼部分也采用XPS挤塑板加工成型，内部装有转轴保证刚度并作为传动轴，外层采用碳纤维布蒙皮，喷涂油漆以保证表面光洁度。自动转动平台底座与叶片本体的下端板通过螺栓连接，平台的转盘通过连接盘与尾缘襟翼的转轴连接，控制自动转动平台可通过转轴带动尾缘襟翼偏转，自动转动平台的定位精度误差为±0.1°。测压试验模型表面共布置62个测压孔，与测压孔连接的压力软管从试验模型下端板开孔处伸出，可与压力扫描阀相连。试验模型的测压孔布置图如图1所示。

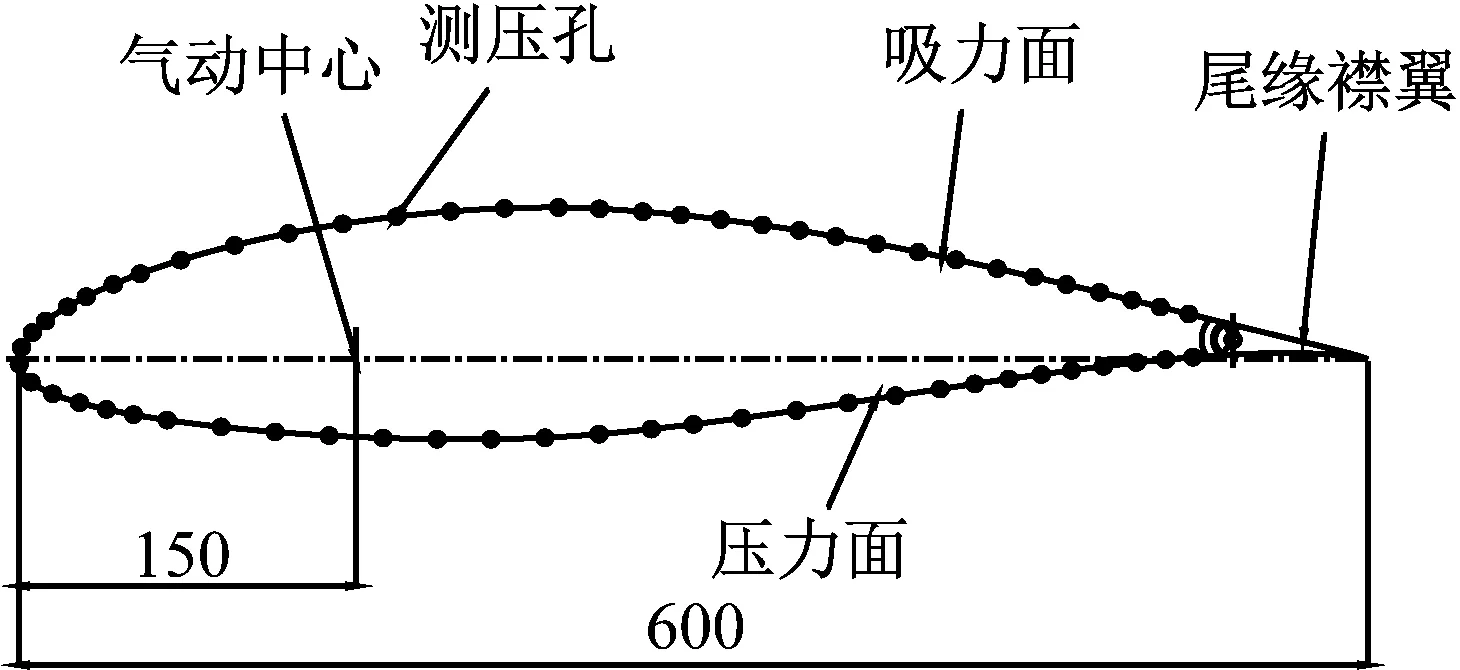
图1 风洞试验模型测压孔布置图

试验模型垂直安装在风洞主测试段的转盘上，通过转盘转动带动试验模型整体转动来调节攻角；试验模型安装时以翼型弦长方向对正风洞测试段转盘的0°刻线，当转盘回零时即为翼型的0°攻角。试验模型的尾缘襟翼通过自动转动平台带动偏转以调节尾缘襟翼偏转角，以尾缘襟翼向压力面偏转为正，向吸力面偏转为负。设定测试风速，可依次测量对应攻角和尾缘襟翼偏转角下的试验模型表面风压数据。风力机尾缘襟翼测压试验方案如图2所示。

(a)试验模型及测量装置布置图

1.2 风洞试验数据处理

测压试验数据可由压力系数分布曲线表示，再通过对压力系数分布曲线进行积分可得到对应攻角下翼型的法向力系数、切向力系数和力矩系数，通过变换计算可得到该攻角下的升力系数、阻力系数等气动参数[15]。

1.2.1 翼型压力系数

试验模型表面压力通常采用无量纲形式的压力系数来表示，压力系数定义为：

(1)

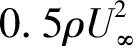
对试验模型表面各个测压点的压力系数离散点进行插值，可以得到翼型的压力系数分布曲线。

1.2.2 气动参数

翼型的法向力系数和切向力系数计算公式如下：

(2)

(3)

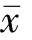
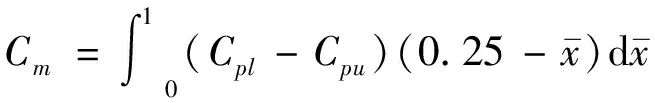
(4)

翼型的升力系数和阻力系数(不包括摩擦阻力)可由法向力系数和切向力系数求得，表达式为：

Cl=Cncosα+Ctsinα

(5)

Cd=Cnsinα-Ctcosα

(6)

式中，α为当前攻角。

1.2.3 气动参数不确定度

风洞试验中翼型升力系数、阻力系数的不确定度与各个测压点的压力系数不确定度相关，压力系数不确定度与来流风速不确定度、压差不确定度、空气密度不确定度相关。各个气动参数的综合不确定度可表示为[16]：

(7)

式中，δ表示各个气动参数的不确定度。

1.3 风力机尾缘襟翼气动性能分析

选择测试风速为16.3 m/s，雷诺数Re=6.2×105，与风力机仿真软件FAST采用的NREL-5MW参考风力机气动参数的雷诺数相似。依次测量攻角分别为-5°，0°，3°，5°，9°，15°，21°，尾缘襟翼偏转角分别为-15°，-7°，0°，7°，15°的试验模型表面风压数据。

1.3.1 翼型压力系数分布曲线

当气流经过翼型时，从翼型前缘附近的驻点起分为二股，分别绕过翼型上、下表面。低速翼型的升力主要是由翼型上、下表面的压力差所造成的，因此可根据翼型的压力系数分布曲线近似地表示升力系数的大小。当压力系数分布曲线所围的面积越大，则翼型的升力系数越大；反之，压力系数分布曲线所围的面积越小则翼型的升力系数越小。

翼型上表面的气流流管截面积收缩比较大，压强急剧下降，产生吸力作用称为吸力面；翼型下表面的压强变化较平缓，称为压力面。对应攻角下的翼型表面压力曲线如图3所示。从图3(a)～(g)可见，在攻角为-5°～21°范围内，随着攻角增大，压力面的压力系数增大，吸力面的压力系数减小，压力系数分布曲线所围的面积逐渐增大，升力系数逐渐增大。同时，在攻角为-5°～15°范围内，尾缘襟翼对压力系数分布曲线的影响较显著，当尾缘襟翼偏转角增大时，吸力面的压力系数减小，压力面的压力系数增大，压力系数分布曲线所围的面积增大，升力系数增大。当攻角增大至21°时，在翼型后缘处(相对弦长x/c>0.5)吸力面的压力系数分布曲线与x轴基本平行，压力系数保持不变，表明该区域已发生附面层分离，翼型在此攻角下已进入失速状态。此时，尾缘襟翼偏转角对翼型表面压力系数的影响明显减小。

从图3可见，尾缘襟翼不仅对尾缘处的气流流动有影响，还对翼型绕流的整个流场有显著的影响。当尾缘襟翼偏转角增大时，使翼型尾缘处形成的涡流低压区扩大，对翼型吸力面的气流有抽吸作用，使吸力面气流流速加快，压力系数减小。同时，尾缘襟翼对翼型压力面的气流有阻滞作用，使气流流速变慢，压力系数增大，从而使翼型上、下表面的压力差增大，升力系数增大。尾缘襟翼偏转角增大也使翼型的弯度增大，对翼型升力系数有一定提升作用。同时，尾缘处的涡流低压区也会使翼型前后压力差增大，从而增大翼型的阻力系数。

(a)-5°度攻角

1.3.2 翼型气动参数

对翼型压力系数分布曲线积分可得到翼型的法向力系数和切向力系数，力矩系数，经变换计算可得到翼型的升力系数和阻力系数，翼型气动参数如图4所示。从图4(a)～(c)可见，在相同攻角下，当尾缘襟翼偏转角增大时，升力系数增大，升力系数曲线向上偏移；阻力系数增大，阻力系数曲线向上偏移；力矩系数减小，力矩系数曲线向下偏移。从图4(d)可见，当攻角较小(约小于3°)时，翼型的升阻比随着尾缘襟翼偏转角增大而增大；此时尾缘襟翼偏转角对升阻比的影响较大。当攻角较大(约大于3°)时，翼型升阻比随着尾缘襟翼偏转角增大而逐渐减小；此时尾缘襟翼偏转角对升阻比的影响较小，升阻比变化趋于平缓。通过不确定度分析，得到风洞试验翼型的升力系数不确定度δCl=±0.09，阻力系数不确定度δCd=±0.03。

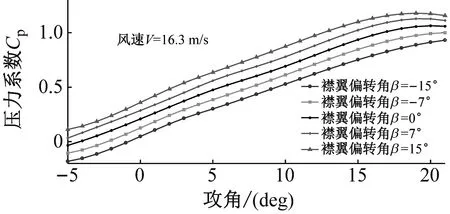
(a)升力系数

1.3.3 翼型气动参数的变化

通过研究尾缘襟翼不同偏转角时翼型气动参数的变化规律，可较直观的分析尾缘襟翼的气动调节性能。尾缘襟翼不同偏转角与襟翼未偏转(0°偏转角)的翼型气动参数差值如图5所示。从图5(a)可见，尾缘襟翼对翼型的升力系数的影响较大，与襟翼未偏转时相比，当尾缘襟翼偏转角为15°时，升力系数增大量可达0.178 5；当尾缘襟翼偏转角为-15°时，升力系数减小量可达-0.184 3，尾缘襟翼可在较大范围内调节翼型的升力系数。在翼型未失速时，尾缘襟翼不同偏转角与0°偏转角的升力系数差值变化量较小，差值变化平缓；当攻角增大至21°时，翼型进入失速状态，该失速点的升力系数差值明显减小，表明尾缘襟翼对升力系数的影响作用明显减小，该趋势与尾缘襟翼对翼型压力系数分布曲线的影响相一致。从图5(b)、5(c)可见，尾缘襟翼偏转角对翼型的阻力系数、力矩系数的影响较小，尾缘襟翼不同偏转角与0°偏转角的阻力系数差值、力矩系数差值较小。

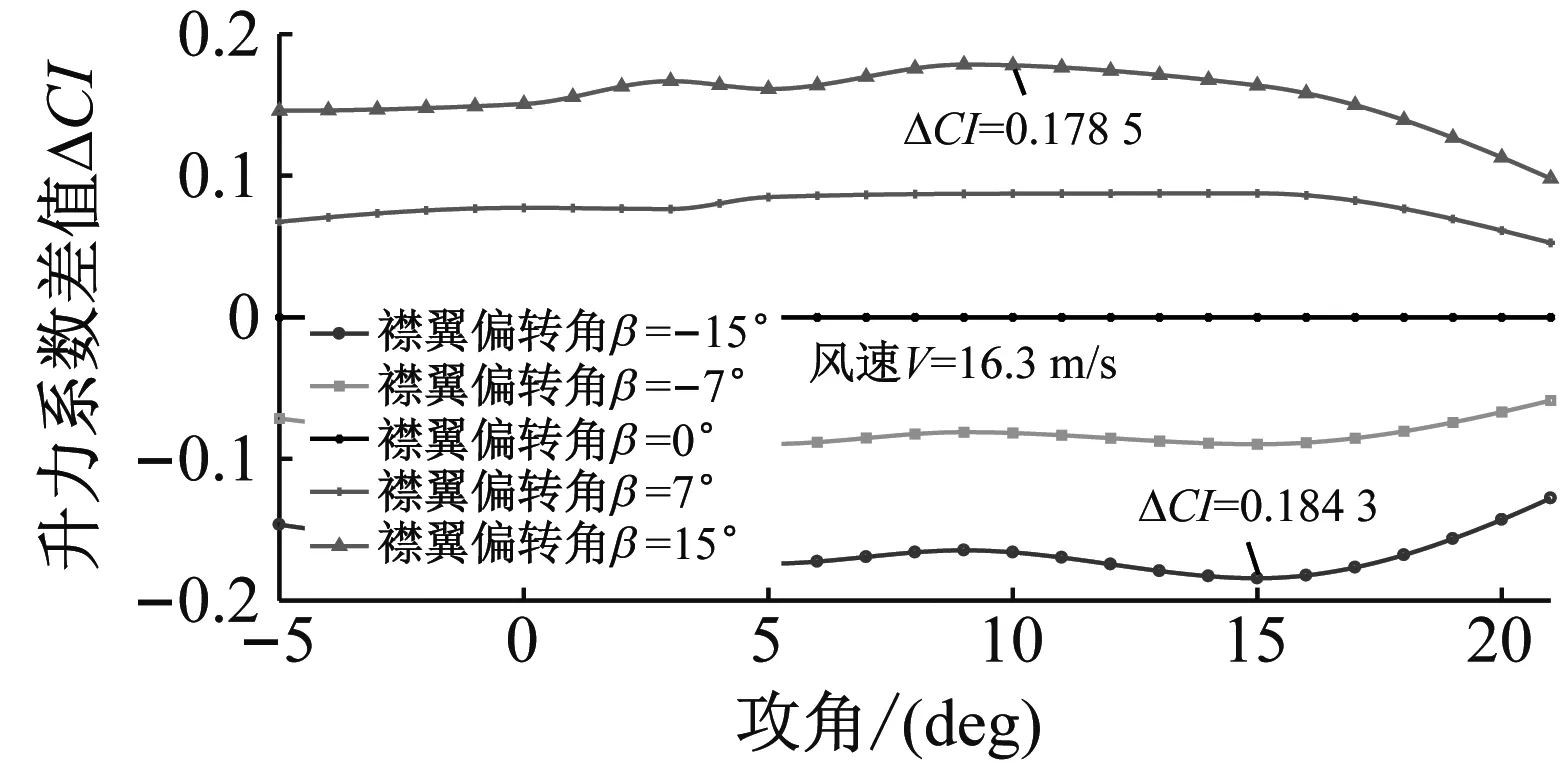
(a)升力系数差值

尾缘襟翼引起的翼型气动参数增大比如图6所示。从图6(a)可见，尾缘襟翼不同偏转角与0°偏转角的升力系数增大比随攻角增大而逐渐减小，当攻角小于0°时，增大比从4逐渐减小到1；当攻角大于0°时，增大比小于1。从图6(b)、6(c)可见，尾缘襟翼不同偏转角与0°偏转角的阻力系数增大比小于1，力矩系数增大比小于0.1。

风洞试验结果表明尾缘襟翼可有效调节翼型的气动参数，并揭示尾缘襟翼对翼型绕流的作用机理和气动参数的调节规律，通过在风力机叶片安装尾缘襟翼可有效调节叶片的气动性能。

2 风力机尾缘襟翼减振控制模拟仿真

2.1 仿真工况

2.1.1 仿真平台

风力机尾缘襟翼减振控制模拟仿真在风力机仿真软件FAST和控制仿真软件MATLAB搭建的联合仿真平台上进行[17]。采用FAST对风力机的气弹响应进行模拟仿真，采用MATLAB对风力机控制策略进行仿真。FAST需进行二次开发以集成尾缘襟翼控制信号接口，然后将FAST编译生成动态链接库，由MATLAB通过S函数调用。将风洞试验得到的尾缘襟翼气动数据，经修正和扩展后制成气动参数表由FAST调用，用于风力机的减振控制模拟仿真。

2.1.2 参考风力机规格参数

模拟仿真算例采用的参考风力机为NREL-5MW风力机，风力机设计规格参数如表1所示[18]。

表1 NREL-5MW参考风力机规格参数

风力机模拟仿真中假设每个叶片各装备一个尾缘襟翼，位于风力机叶片展长66%～96%处，该处翼型为NACA 64618，尾缘襟翼占弦长为10%。风力机尾缘襟翼沿叶片的布置和形态如图7所示。

(a)尾缘襟翼布置图

2.1.3 尾缘襟翼气动参数

考虑风洞试验模型的展弦比，对翼型的气动参数进行修正[19]。尾缘襟翼未偏转时，修正后的翼型升力系数风洞试验数据、Xfoil计算数据、NREL仿真数据对比如图8所示。通过对比表明，风洞试验数据与Xfoil计算数据、NREL仿真数据在在零升力攻角附近的范围内有较好的一致性。

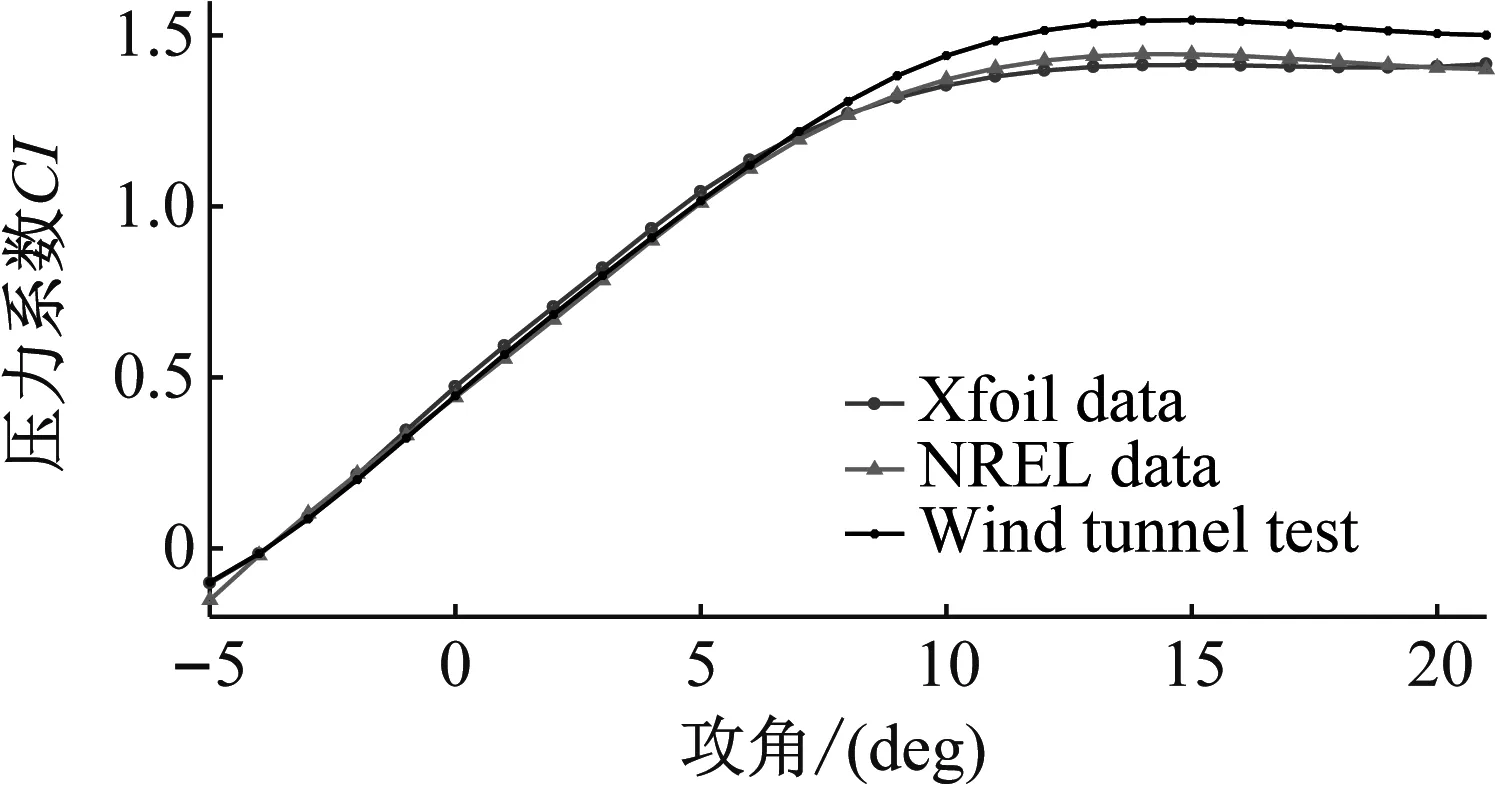
图8 修正后的升力系数对比

由于Xfoil计算得到的数据便于扩展，故风力机整机仿真采用Xfoil计算得到的尾缘襟翼气动参数进行仿真计算。扩展后的翼型全攻角升力系数(攻角±180°，尾缘襟翼偏转角±15°)如图9所示。

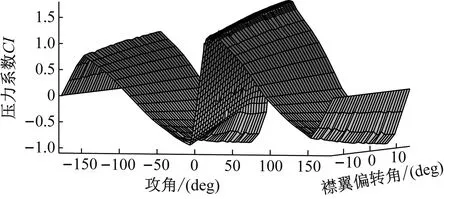
图9 翼型全攻角升力系数

2.1.4 独立变桨距和尾缘襟翼协同控制策略

风力机叶片降载减振控制的基本原理为：当三个叶片的叶片荷载(一般取叶根挥舞弯矩)在轮毂坐标系的投影分量(即轮毂俯仰力矩，偏航力矩)可视为不平衡量。当轮毂俯仰力矩和偏航力矩不为零时，通过控制系统调动叶片变桨距和尾缘襟翼偏转，调节叶片的桨距角和尾缘襟翼的偏转角改变叶片的气动性能，从而降低叶根弯矩的不平衡量，降低叶根弯矩且减小叶片变形。

根据风力机独立变桨距控制和尾缘襟翼控制的特点，设计独立变桨距和尾缘襟翼协同控制策略。该控制策略采用荷载分频控制算法，以叶根挥舞弯矩作为输入信号，通过滤波得到低频荷载分量(1P，once per revolution)和高频荷载分量(2P)，独立变桨距控制环主要用于控制1P频率的荷载及振动，尾缘襟翼控制环主要用于控制2P频率的荷载及振动。叶根挥舞弯矩的1P频率分量和2P频率分量经多叶片坐标变换后，投影到轮毂坐标的俯仰分量和偏航分量可看作近似独立，可分别采用PID控制器进行控制。在独立变桨距控制器上叠加叶片方位角前馈控制可提高变桨距控制系统的响应性。风力机独立变桨距和尾缘襟翼协同控制策略如图10所示。

图10 风力机独立变桨距和尾缘襟翼协同控制策略示意图

2.1.5 仿真工况

仿真设定的工况侧重于正常发电的风力机疲劳荷载计算。根据IEC 61400-1的DLC 1.2工况[20]，设定湍流风属于IIB类，普通湍流模式，采用Von Karman风谱模型，参考风速为42.5 m/s，湍流强度为0.14；轮毂高度平均风速为20 m/s，风剪切指数为0.2。湍流风数据由湍流风模拟器Turbsim程序生成，风力机轮毂高度的风速如图11所示。

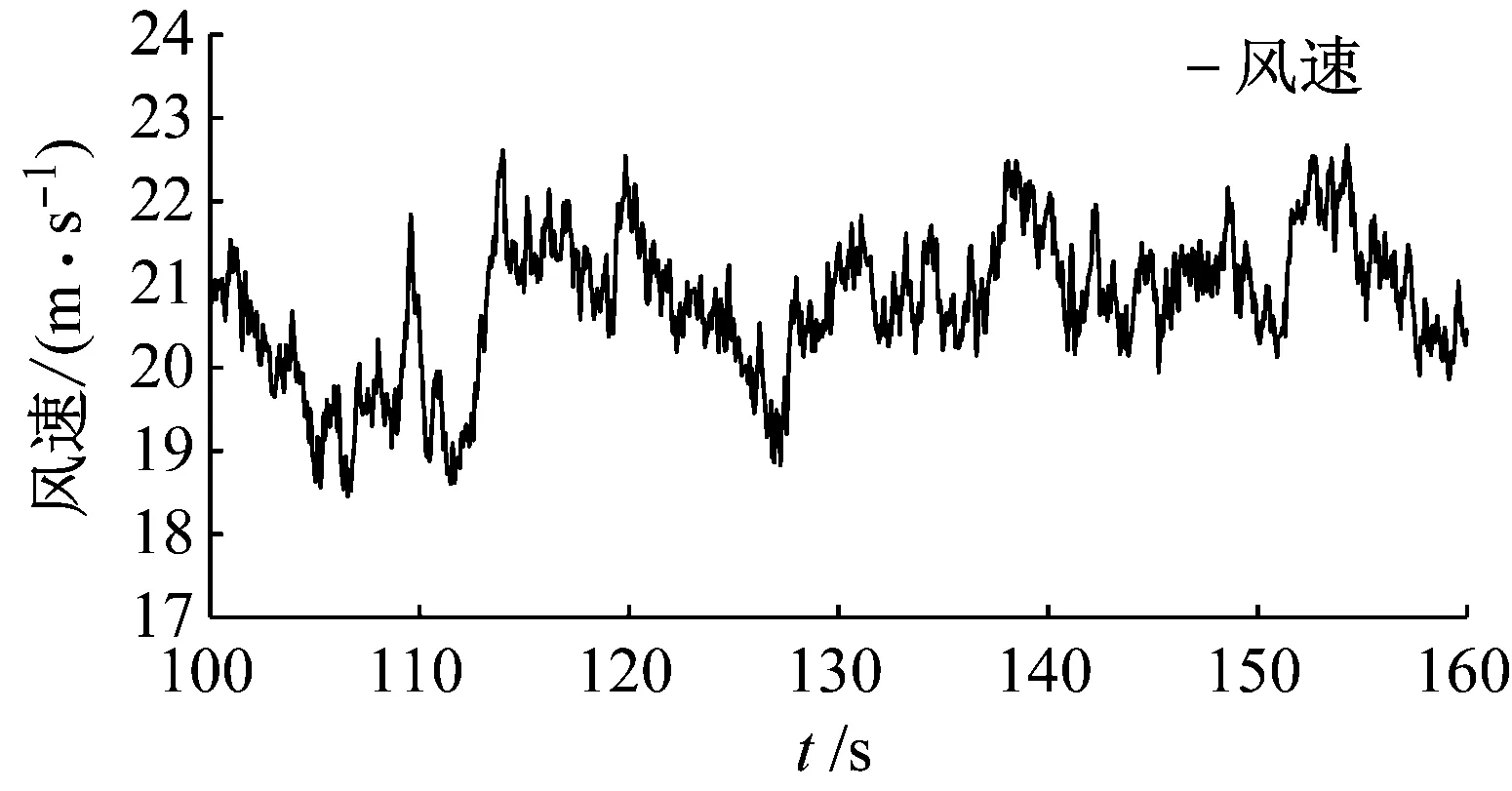
图11 轮毂高度风速

2.2 仿真结果及讨论

对比风力机采用整体变桨距控制，独立变桨距控制，独立变桨距和尾缘襟翼协同控制三种控制策略的叶片荷载及振动情况，取仿真时间为100～160 s的仿真结果进行讨论。

2.2.1 风力机叶根弯矩

风力机采用整体变桨距控制，独立变桨距控制，独立变桨距和尾缘襟翼协同控制的叶根弯矩如图12所示，叶根弯矩振幅标准差数据如表2所示。如图12(a)所示，采用整体变桨距控制时叶根挥舞弯矩的振幅较大；采用独立变桨距控制时叶根弯矩振幅明显减小，标准差减少了58%；采用独立变桨距和尾缘襟翼协同控制时挥舞弯矩振幅进一步减小，标准差减少了64.8%。由于叶片疲劳荷载主要是由风荷载的波动引起的，减小风荷载振幅将有利于减轻风力机叶片的疲劳荷载。如图12(b)所示，采用独立变桨距控制、独立变桨距和尾缘襟翼协同控制时，叶片摆振弯矩的振幅也有所降低。

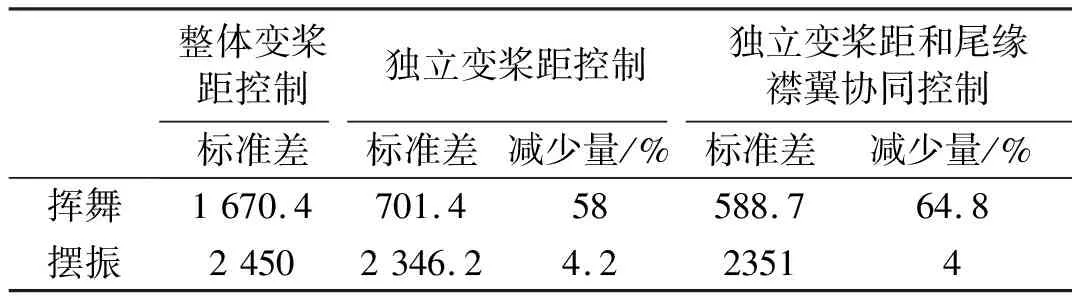
表2 叶根弯矩标准差

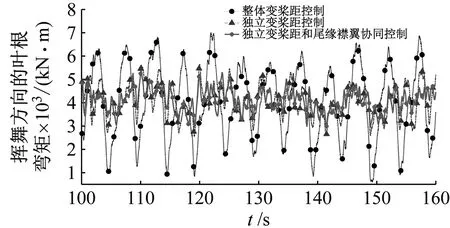
(a)挥舞方向的叶根弯矩

风力机独立变桨距与尾缘襟翼协同控制通过改变叶片攻角和尾缘襟翼偏转角，调用对应的升力系数、阻力系数等气动参数，从而改变叶片气动性能。气动参数变化对叶片的挥舞弯矩和摆振弯矩均有影响，且由于控制系统的输入信号是叶根挥舞弯矩，故挥舞弯矩的控制效果明显，摆振方向的控制效果不明显。

2.2.2 风力机叶片振动

风力机采用整体变桨距控制，独立变桨距控制，独立变桨距和尾缘襟翼协同控制的叶片振动(叶尖变形)如图13所示，叶片振动振幅标准差数据如表3所示。如图13(a)所示，采用整体变桨距控制时挥舞方向的叶片振动的振幅较大；采用独立变桨距控制时叶片振动振幅明显减小，标准差减少了50.6%；采用独立变桨距和尾缘襟翼协同控制时叶片振动振幅进一步减小，标准差减少了56.7%。如图13(b)所示，采用独立变桨距控制、独立变桨距和尾缘襟翼协同控制时，摆振方向的叶片振动振幅也有一定程度的降低。

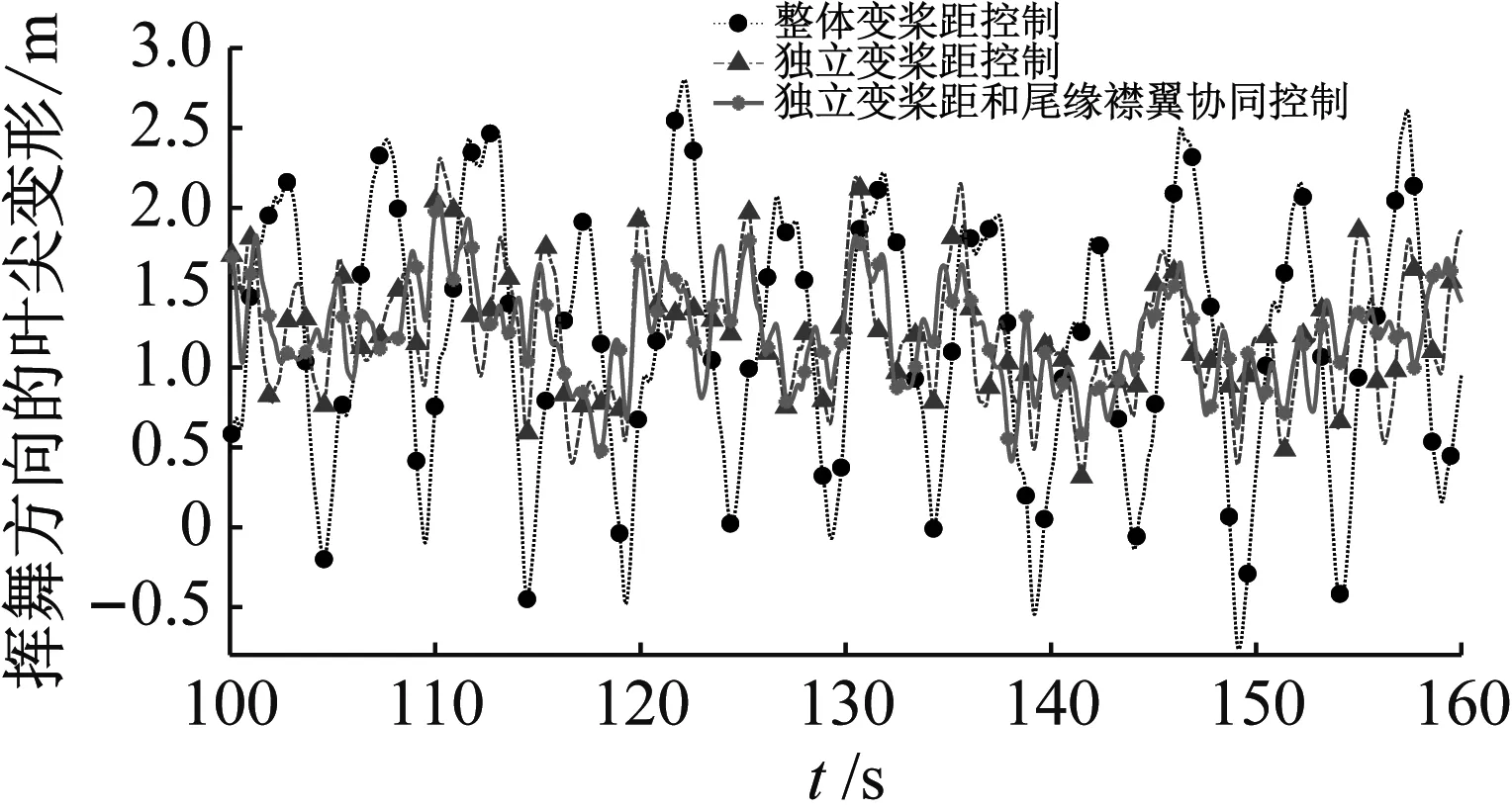
(a)挥舞方向的叶尖变形

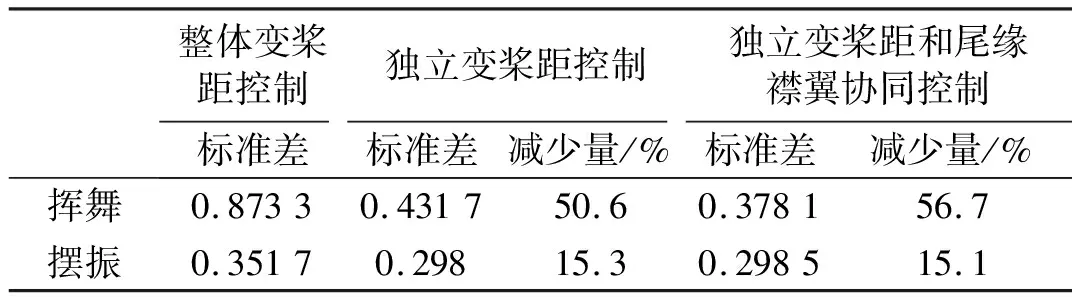
表3 叶尖变形标准差

2.2.3 叶片振动功率谱密度分析

风力机采用整体变桨距控制，独立变桨距控制，独立变桨距和尾缘襟翼协同控制三种控制策略的挥舞方向叶片振动功率谱密度分析如图14所示。从图中可见，采用整体变桨距控制时1P频率处(约0.2 Hz)和2P频率处(约0.4 Hz)存在较高的频峰。采用独立变桨距控制时1P频率处的频峰峰值明显降低；采用独立变桨距和尾缘襟翼协同控制时1P频率和2P频率处的频峰峰值都明显降低。在控制策略设计中独立变桨距控制主要用于减缓1P频率的振动，而尾缘襟翼控制主要用于减缓2P频率的振动，仿真结果与控制策略设计的预期结果一致，表明独立变桨距控制和尾缘襟翼协同控制对风力机叶片的振动有较好的控制效果。

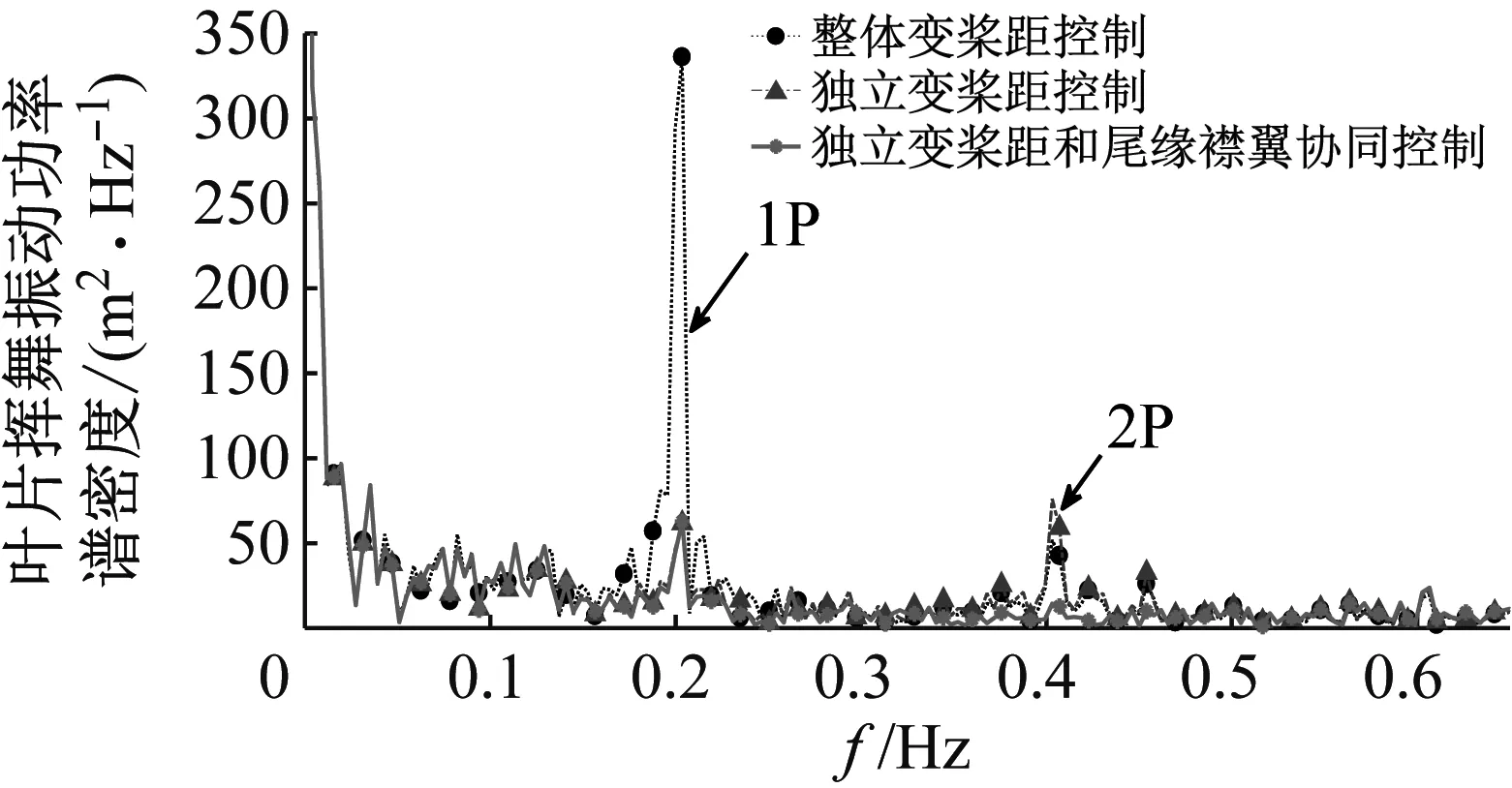
图14 风力机挥舞方向的振动功率谱密度分析

2.2.4 等效疲劳载荷分析

采用雨流计数法对叶根挥舞弯矩、摆振弯矩的等效疲劳荷载进行分析。叶片为复合材料，故S-N斜率取10。计算得到风力机采用整体变桨距控制，独立变桨距控制，独立变桨距与尾缘襟翼协同控制三种控制策略的的等效疲劳荷载如图15所示，等效疲劳荷载数据如表4所示。采用整体变桨距控制时叶根挥舞弯矩等效疲劳荷载为2 340 kN·m；采用独立变桨距控制时叶根挥舞弯矩等效疲劳荷载为1 110 kN·m，比整体变桨距控制降低了52.6%；采用独立变桨距与尾缘襟翼协同控制时叶根弯矩等效疲劳荷载为845 kN·m，比整体变桨距控制降低了63.9%。采用独立变桨距控制，独立变桨距与尾缘襟翼协同控制时，叶根摆振弯矩也有一定程度的降低。

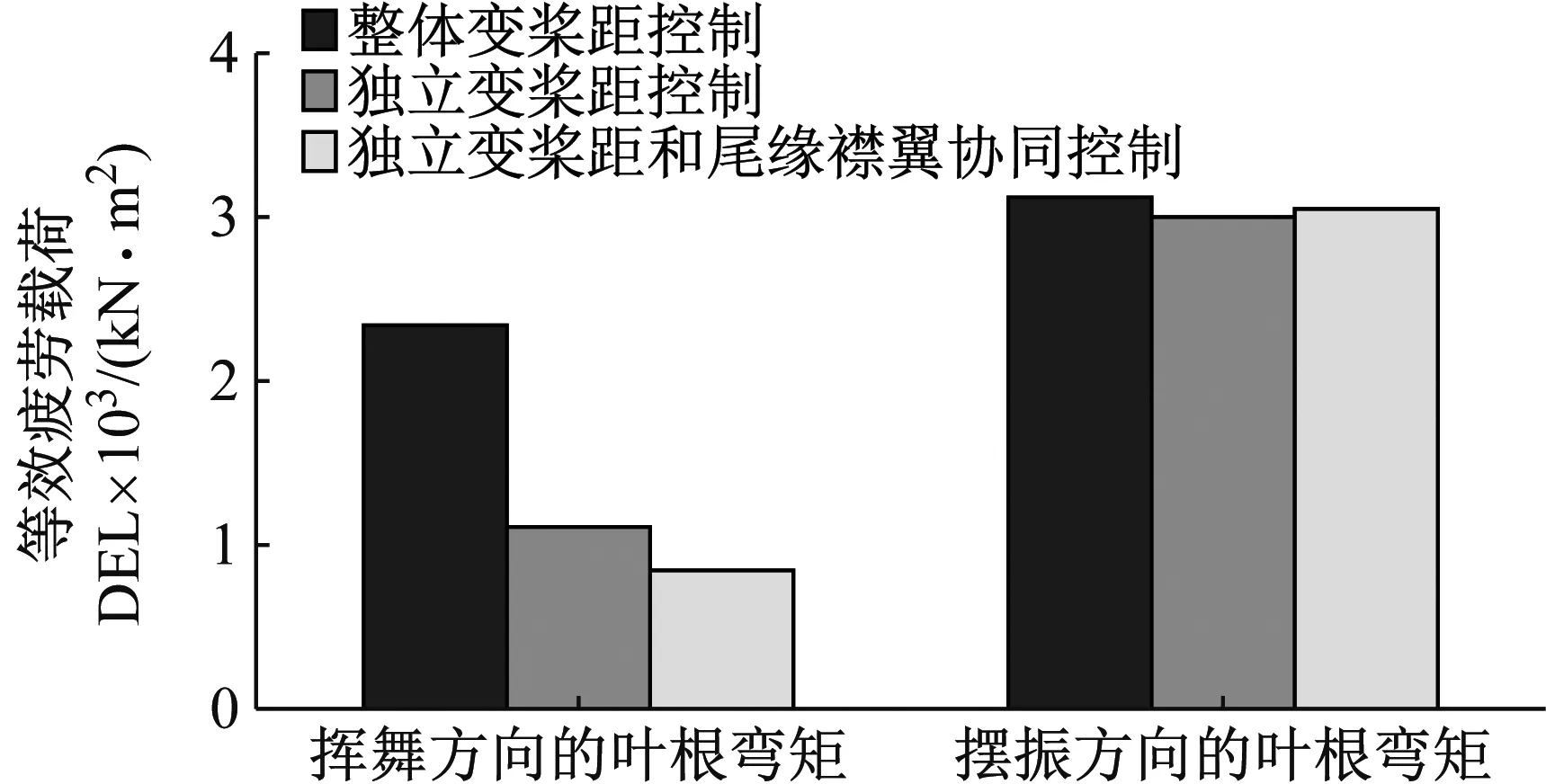
图15 等效疲劳荷载分析

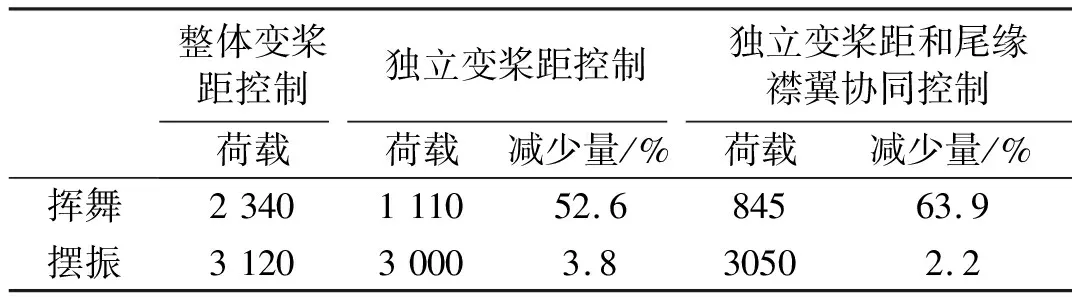
表4 等效疲劳载荷DEL

3 结 论

本文通过风洞试验研究风力机尾缘襟翼的气动特性，并通过模拟仿真研究尾缘襟翼与独立变桨距协同控制对风力机叶片的减振性能，得到的主要结论如下：

(1)尾缘襟翼对翼型绕流有显著的影响。当尾缘襟翼偏转角增大时，使吸力面气流速度加快，压力系数减小；同时，压力面气流流动速度减小，压力面的压力系数增大。当攻角增大至翼型进入失速点后，尾缘襟翼对翼型的压力系数分布的影响作用显著减小。

(2)风力机尾缘襟翼可有效调节翼型的气动参数。尾缘襟翼偏转角增大时，翼型的升力系数增大，升力系数曲线向上偏移。当攻角小于3°时，翼型的升阻比随着尾缘襟翼偏转角增大而增大；当攻角大于3°时，翼型升阻比随着尾缘襟翼偏转角增大而减小；且尾缘襟翼偏转角对翼型升阻比的影响随攻角增大而逐渐减小。

(3)根据尾缘襟翼对高频振动响应速度快的特点，设计尾缘襟翼和独立变桨距协同控制策略，设计风力机尾缘襟翼和独立变桨距协同控制策略，独立变桨距主要控制低频荷载及振动，尾缘襟翼主要控制高频荷载及振动。仿真结果表明，风力机独立变桨距控制使叶根挥舞弯矩等效疲劳荷载降低了52.6%，挥舞方向振动标准差减小了50.6%；尾缘襟翼与独立变桨距协同控制使叶根挥舞弯矩等效疲劳荷载进一步降低了63.9%，挥舞方向振动标准差减小了56.7%。风力机尾缘襟翼和独立变桨距协同控制对叶片具有较好的降载减振作用。