插板透水丁坝拦沙作用数值模拟研究
2021-08-11李玉建耿义鑫
毛 亮,李玉建,李 鹤,2,耿义鑫
(1.新疆农业大学水利与土木工程学院,乌鲁木齐 830052;2.新疆水利水电勘测设计研究院,乌鲁木齐 830000)
1 研究背景
河道整治及水沙防治方面多以透水丁坝为主,就功能作用特点及结构优势而言,透水丁坝具有透水孔以透水为目的,产生的回流很小,可以起到拦沙和淤滩作用[1-2].此前,大部分学者主要对透水丁坝水沙调控性能[3-4]、丁坝坝后回流淤积[5]、丁坝附近冲刷[6-7]等进行了研究,随后学者们又对丁坝拦沙机理[8]、拦沙量与减蚀量计算[9-10]和拦沙效应时间变化[11]等展开了部分研究.何富荣等[12-13]研究了水力插板在航道拦沙过程中的应用与其特殊的拦沙作用优势.李浩等[14]研究了沙棘“柔性坝”阻水拦沙作用,结果表明,不同水沙参数情况下柔性坝周围含沙量不同,从上游往下游逐渐呈减小趋势.彭程等[15]对沉沙池内拦沙帘的拦沙特性进行了试验研究,结果表明,拦沙帘对泥沙粒径较大的泥沙截沙率较高.Lien[16]通过试验分析了拦沙坝对水沙拦截效率,并且给出了过流量比例和储存量比例系数定义.在2002—2003年期间新疆农业大学对植物坝拦沙进行了室内试验,得出了其阻水、拦沙作用以及削减水流剪切应力,减小泥沙输移比,起到拦沙作用[17-19].插板透水丁坝作为一种新型结构护岸整治建筑物,相对于其他结构型式透水建筑物具有极大的优越性,而对于插板透水丁坝拦沙相关问题缺乏研究,截至目前还未有人对插板透水丁坝拦沙作用进行研究.本文通过数值模拟方法计算分析不同因素下插板透水丁坝坝前河道断面含沙量变化来研究插板透水丁坝拦沙作用,为我国西北部地区,尤其在新疆干旱区内陆河河道演变治理与生态修复等工作提供了新的研究思路.
2 数值模型及验证
2.1 控制方程
2.1.1 连续性方程

2.1.2 动量方程
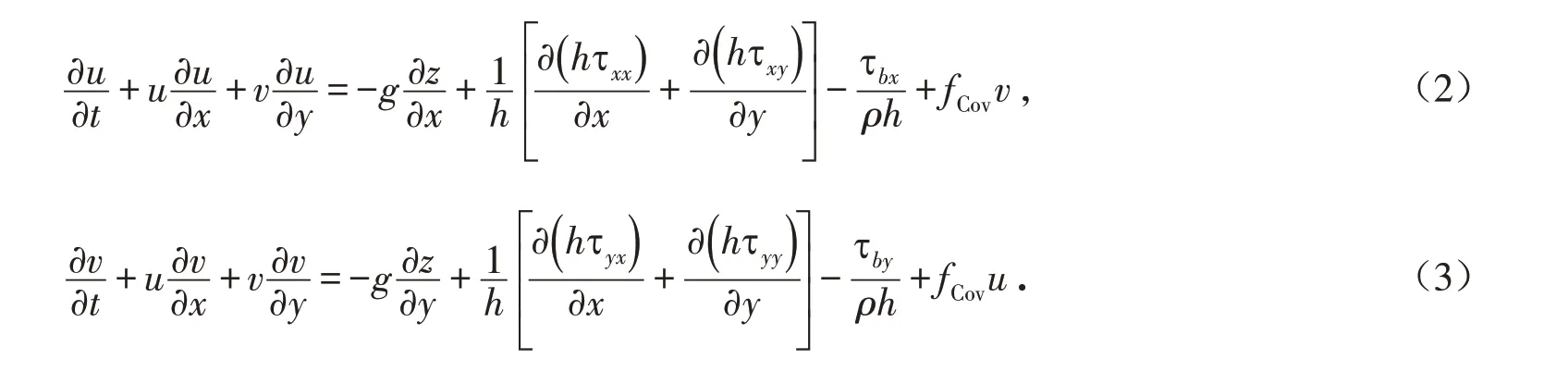
式中:u和v为垂线平均流速在x和y方向上分量;g为重力加速度,m/s2;z为水面高程,m;ρ为水密度,kg/m3;h为当地水深,m;fCov为科氏力系数;τb表示河床切应力,τxx,τxy,τyy和τyx为垂线平均雷诺应力.
2.1.3 泥沙输移 根据CCHE2D软件采用以悬移质泥沙为主的全沙非平衡输沙模型,悬移质泥沙输移方程如式(4)所示:
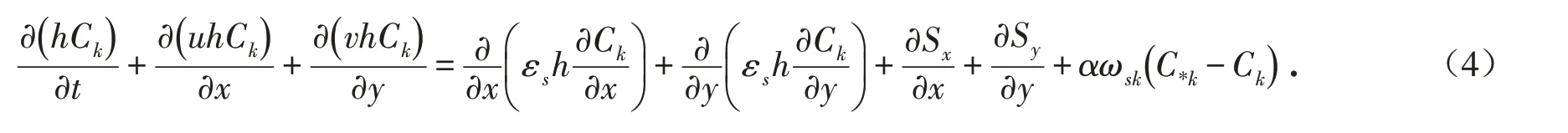
式中:Ck平均悬移质浓度,kg/m3;C*k平衡状态下悬移质的容重,kg/m3;εs沉积物的湍流扩散系数;ωsk沉积物沉降速度,m/s;α为非平衡适应系数;k=1,2,…,N.
2.2 数值模型
数值模拟基于张凯[20]物理模型试验,如图1所示.选取塔里木河新其满河段洪水流量Q=16.03 L/s作为典型流量,在长6 m、宽1.2 m、高0.45 m、底坡坡降i=1/500的混凝土水槽中进行,模型比尺为:水平比尺λL=93,垂直比尺λH=25,几何变率比尺e=10,流速比尺λV=5,流量比尺λQ=83 407.93,粒径比尺λd=0.93,比降比尺λJ=0.1,时间比尺λt=50,河床糙率比尺λn=0.54.针对不同因素,共设计9种试验方案,选取插板透水丁坝开孔率为30%[20],插板透水丁坝采用单一正挑布置的方式,插板均匀布置在水槽中.
根据图1水槽模型,建立本文数值模型如图2.首先建立模型地形文件,用CCHE-MESH结构化网格对模型网格进行划分,用边界模块连接各边界点,以此形成模型边界,再对边界线进行优化并划分网格,取Imax=100,Jmax=300,网格数量共计30 000个(除加密网格点).运用双边界代数网格形成初始网格,为了提高计算精度,对插板透水丁坝周围网格进行局部加密,并使用RL正交网格(带光滑函数-1)来提高全区域网格的光滑性、正交性,以达到网格质量优化.设定初始条件,采用实测物理模型地形高程数据,再用四边形平面插值的方法,水槽模型设置了一个进口边界和一个出口边界.初始水面高程根据实测值设置,进口水面高程为0.841 m,出口断面水面高程为0.826 m,壁面采用无滑移条件,糙率n=0.010.对于自由液面的处理,不需要对其设置,采用软件默认自由液面,将处理好的网格文件导入CCHE-GUI进行模拟计算.
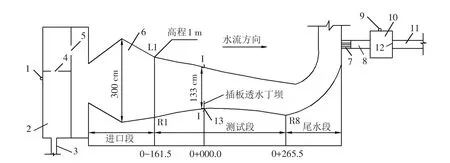
图1 水槽模型平面图Fig.1 Plan of flume model
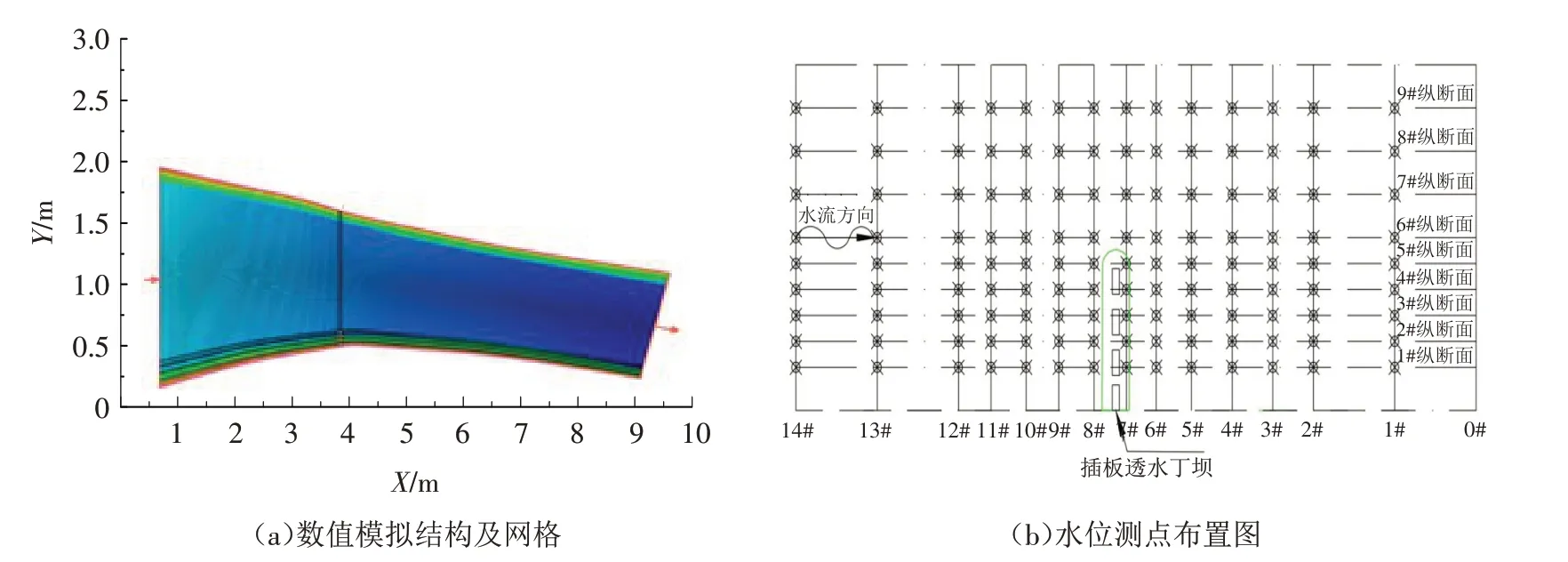
图2 插板透水丁坝数值模拟及测点布置图(俯视图)Fig.2 Layout of numerical simulation and measuring points of permeable sheet piling spur dike(top view)
根据塔里木河其满河段河床性质、流量及泥沙特征[20],对模拟影响因素参数进行确定.模拟最大流量选取20 a一遇洪水流量16.03 L/s(相当于原型1337 m3/s),由于塔里木河河床为粉细沙河床,粒径为0.050~0.086 mm,结合其满河段实际情况,选用有效坝长为25、30、35 cm的插板透水丁坝.
当流量为Q=16.03 L/s、泥沙粒径d=0.050 mm、有效坝长L=25 cm工况下,选取物理实测数据与数值模拟数据进行对比,结果发现两条曲线各点基本吻合,说明数值模拟可以准确进行模拟试验,具体见图3.
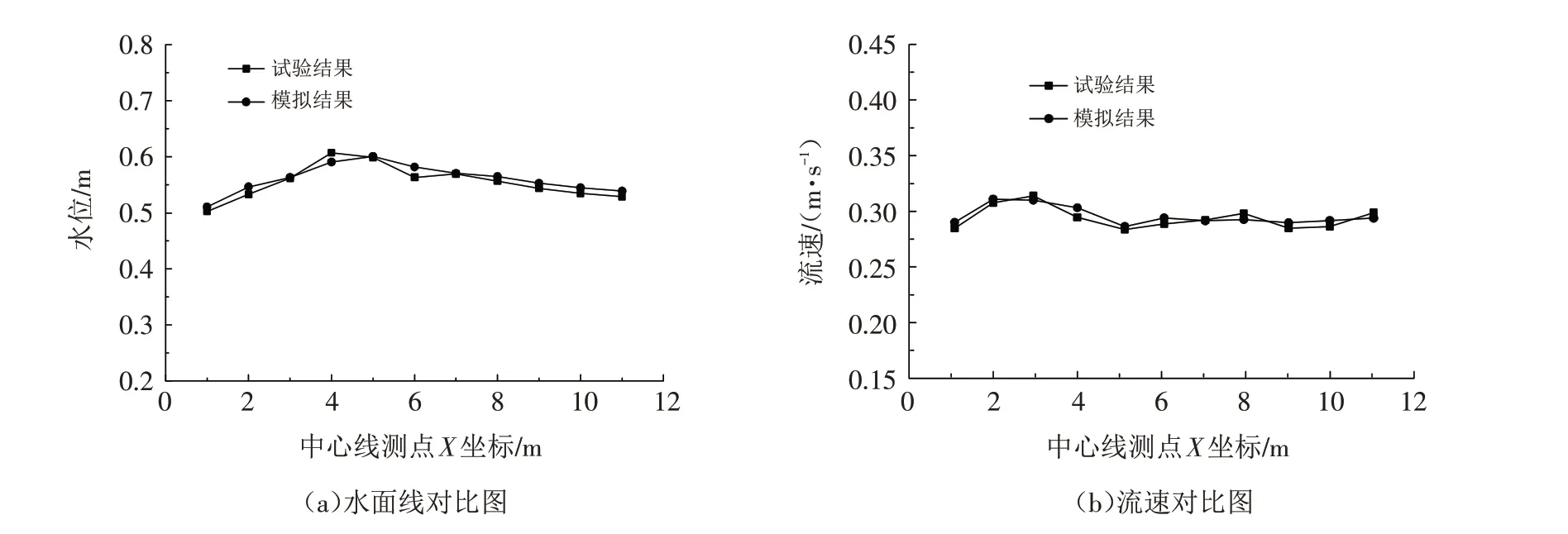
图3 试验结果与模拟结果对比图(7#纵断面)Fig.3 Comparison of test results and simulation results(7#vertical section)
2.3 拦沙指标
拦沙量是指有插板透水丁坝时横断面(8#断面)含沙量与无插板透水丁坝(8#断面)时横断面含沙量之差,即:

拦沙比是指拦沙量与有插板透水丁坝时横断面(8#断面)含沙量之比,即:

式中:CS拦为插板透水丁坝拦沙量;CSy8为有插板透水丁坝时横断面(8#断面)含沙量;CSw8为无插板透水丁坝时横断面(8#断面)含沙量;φ表示拦沙比.
3 计算结果分析
3.1 流量对拦沙作用影响
保持有效坝长和泥沙粒径不变,选取开孔率为30%,挑角90°,流量为10.28、13.07、16.03 L/s进行模拟计算.取坝前8#横断面含沙量计算结果,并绘制含沙量相关曲线(如图4).
流量改变对插板透水丁坝附近水沙运动具有一定影响.水槽中布置插板透水丁坝,由于插板透水丁坝对水沙具有挑流消能以及阻水缓流等作用,丁坝附近泥沙含沙量发生变化.通过对有无插板透水丁坝时8#横断面含沙量变化分析,随着流量减小,水流中泥沙运动趋于缓慢,越靠近插板透水丁坝运动速度越慢,这样虽不能反映真实的运动情况,但可以定性地反应插板透水丁坝坝前含沙量变化.
图4 a为插板透水丁坝坝前8#横断面含沙量分布、流量和拦沙比与拦沙量分布,可以看出含沙量沿着8#横断面从右岸往左岸逐渐增大,并在坝头附近含沙量达到最大值.插板透水丁坝布置在河道右岸边,插板透水丁坝坝前横断面随着流量的增大,水流中泥沙含沙量增大,在坝前拦沙量减小.这是由于流量增大,同时水流流速也增大,水流中携带泥沙量增多并通过主流区输送下游,丁坝具有束水攻沙的作用.由图4 b可知,流量与拦沙比呈负相关、与拦沙量呈正相关.
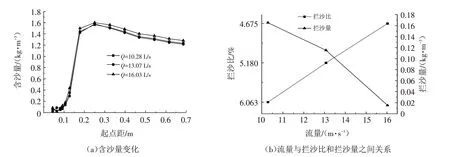
图4 坝前8#断面试验结果Fig.4 Test results of 8#cross section in front of spur dike
结果表明,插板透水丁坝拦沙量(比)与水沙条件有密切联系,随着流量增大,插板透水丁坝坝前拦沙比越小,同时拦沙量减小.其他条件不变时,流量越大,水流流速越大,水流中携带泥沙量也越多,由于插板透水丁坝阻水缓流与挑流作用,使悬沙横向输移,最后通过丁坝主流区束水攻沙,最终使丁坝拦沙量(比)减小,由此看来,插板透水丁坝具有拦沙作用.
3.2 泥沙粒径对拦沙作用影响
保持流量和有效坝长不变,选取开孔率为30%,挑角90°,泥沙粒径为0.050、0.068、0.086、0.104、0.122 mm进行模拟计算.取坝前8#横断面含沙量计算结果,并绘制含沙量相关曲线(图5).
在流量和有效坝长一定的情况下,通过改变水流中泥沙粒径大小来观测插板透水丁坝坝前8#横断面含沙量变化,分析插板透水丁坝拦沙作用.同一流量同一坝长下,随着泥沙粒径增大,8#断面含沙量逐渐增大,拦沙比增大,但增加幅度相对较小,拦沙效果显著.
图5 a为插板透水丁坝坝前8#横断面含沙量的变化情况,可以看出在0~0.25 m处,含沙量随着泥沙粒径增大而减小,而且泥沙粒径越小,含沙量变化也越大,含沙量最大值出现在泥沙粒径d=0.050 mm,最大值约2.0 kg/m3.每种不同泥沙粒径,其含沙量最大值出现在坝头附近,在距坝头0.25 m处,含沙量变化开始趋于平缓,而且d=0.068 mm要比d=0.086、0.104、0.122 mm在主流区含沙量高,d=0.122 mm变化幅度比较大.图5 b可以看出,泥沙粒径与拦沙比呈负相关,与拦沙量呈正相关关系.
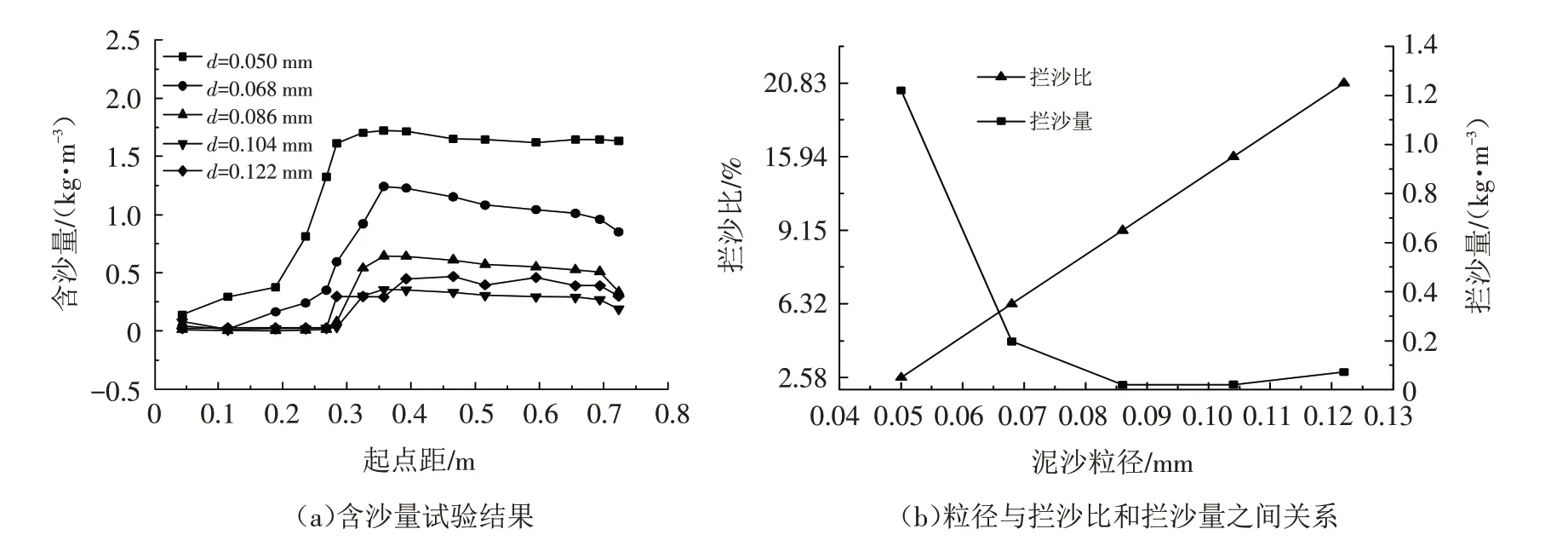
图5 坝前8#断面试验结果Fig.5 Test results of 8#cross section in front of spur dike
结果表明,插板透水丁坝拦沙量(比)与水流中泥沙粒径有很大关系,泥沙粒径越大,坝前水流流速越小,大颗粒粒径水沙搬运速度越低,通过丁坝作用将其拦截在丁坝前.随着泥沙粒径增大,拦沙量增大,同时丁坝拦沙比增大,由于粗粒径沉降速度快,需要更大的启动速度,大量粗颗粒泥沙被拦截在丁坝前,从而表明插板透水丁坝在河道中具有拦沙作用,且具有拦截粗沙的作用.
3.3 有效坝长对拦沙作用影响
保持流量和泥沙粒径不变,选取开孔率30%,挑角90°,有效坝长为25、30、35 cm进行模拟计算.取坝前8#横断面含沙量计算结果,并绘制含沙量相关曲线(图6).
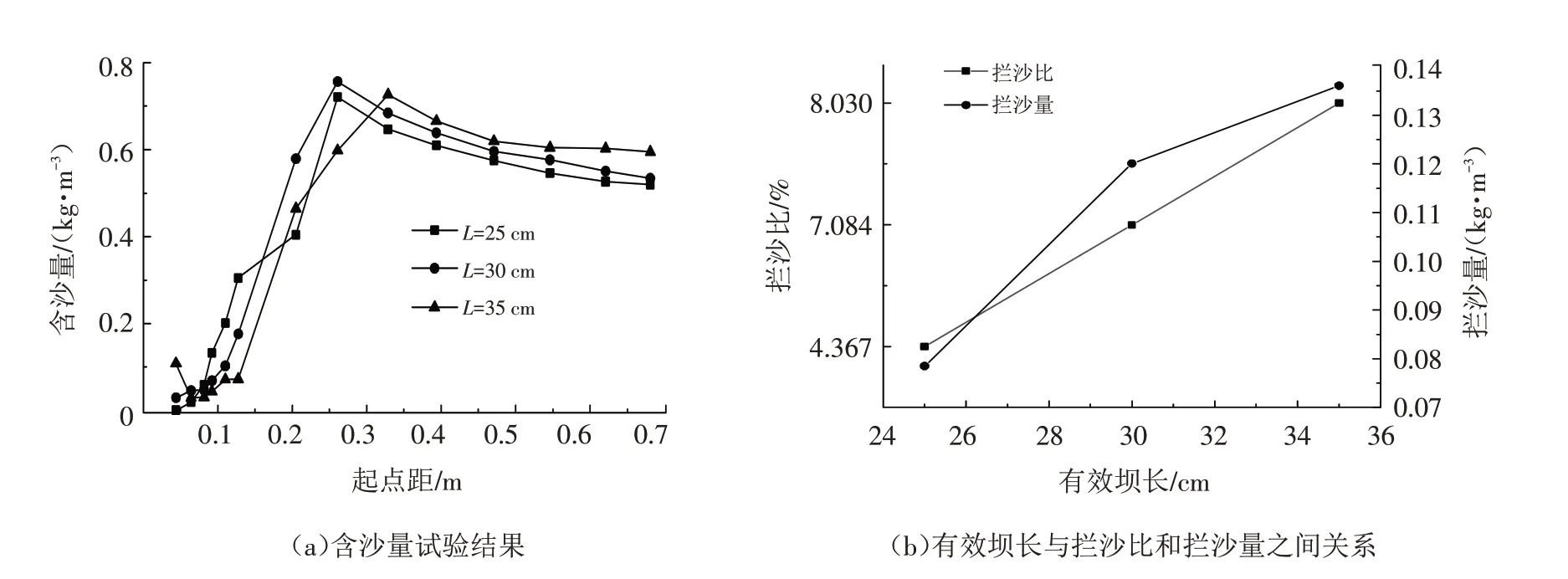
图6 坝前8#断面试验结果Fig.6 Test results of 8#section in front of spur dike
流量和泥沙粒径一定,改变插板透水丁坝有效坝长来观测8#横断面含沙量变化.同一流量同一泥沙粒径下,随着插板透水丁坝有效坝长增加,丁坝前壅水面积增大,丁坝阻水缓流作用增强,拦沙量逐渐增加,但增加幅度不大.图6 a所示为插板透水丁坝8#横断面含沙量变化情况,可以看出坝前含沙量逐渐增大,不同有效坝长,含沙量最大值出现的位置不同,其最大值都出现在坝头附近,并且在有效坝长为30 cm时,含沙量最大值最先达到.主要是由于插板透水丁坝有效坝长越长,其阻水缓流和挑水分流作用越强,导致上游丁坝作用区面积增大,大量水沙速度减缓,水流中泥沙被其拦截,主流区束窄宽度提高.图6 b所示为拦沙比和拦沙量与有效坝长之间的关系,可以看出,有效坝长与拦沙量、拦沙比呈递增关系,有效坝长越长,拦沙效果越好.
结果表明,流量和泥沙粒径一定,随着有效坝长增加,插板透水丁坝坝前缓流阻水面积增大,阻流与引水挑流能力增加,束窄宽度增加,拦截效果明显.
3.4 插板透水丁坝某一断面平均流速
1)天然河道
天然河道某一过水断面平均流速的计算,通常采用R.Maning公式[21]:

式中:U为河道某一过水断面平均流速,m/s;n0为河道糙率;R为河道水力半径,m;Jp为河道水力坡度.当河流为天然游荡型宽浅河床时,水力半径可以用河道平均水深代替(即:h≈R).
2)透水丁坝下游平均流速
透水丁坝下游平均流速公式[22]:

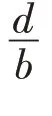
本文通过李玉建[22]推导的透水丁坝下游平均流速公式,概化径距比(d/b)约等于L×p(坝长与开孔率乘积),用数值模拟计算结果验证插板透水丁坝减缓流速及拦沙作用,即:

3)插板透水丁坝下游平均流速
无插板透水丁坝时河道下游平均流速:
河道平均水力坡度Jp=0.014 6,河道试验糙率n0=0.010,试验下游平均水深hB1=0.275 6 m,下游过水断面的平均流速:
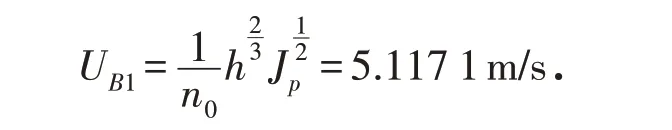
有插板透水丁坝下河道下游平均流速:
丁坝长L=0.25 m,p=30%,试验下游平均水深hB2=0.224 3 m,插板透水丁坝处水位差∇z:
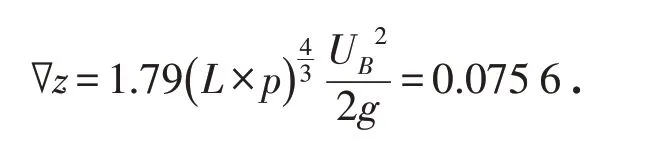
下游过水断面的平均流速:
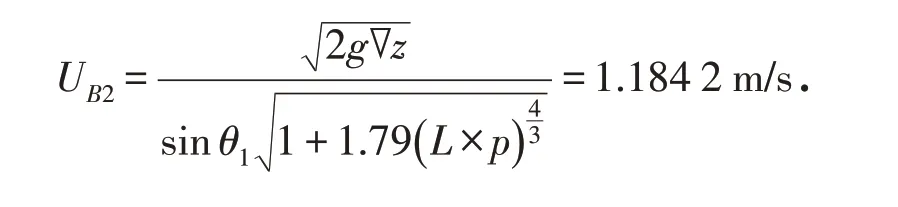
以上计算可看出:UB1>UB2,证明插板透水丁坝有缓流作用,在插板透水丁坝作用下,下游河道平均流速降低,对水沙具有拦截作用,展现出插板透水丁坝在河道水沙治理的优越性.
4 结论
1)插板透水丁坝能减小水流中悬-推移混合质运动速度,使坝前泥沙含沙量增大,证明了插板透水丁坝具有拦沙作用.插板透水丁坝拦沙作用除了与来沙条件、丁坝结构型式有关外,还可能与水流含沙量、河床边界条件有关,有待进一步研究.插板透水丁坝对泥沙拦截作用是解决干旱区内陆河泥沙治理的一种有效方法,并具有创新意义.
2)从粒径分布来看,粗粒泥沙含沙量表现为先增大后减小,粗粒泥沙最先落淤,被插板透水丁坝拦截坝前;细颗粒泥沙含沙量先减小后增大,细颗粒泥沙坝前淤积少,大部分透过开水孔落淤坝后,证明了插板透水丁坝对泥沙具有“拦粗排细”分选作用.
3)随着插板透水丁坝有效坝长增加,坝前壅水面积增大,丁坝阻水缓流作用增强,水流中泥沙被拦截,拦沙量增加;流量越大,水流流速越大,水流中携带泥沙量越多,由于插板透水丁坝阻水缓流与挑流作用,使悬沙横向输移,从而证明了拦沙作用显著.
