基于改进Jensen不等式的中立型时滞系统稳定性判据
2021-08-11杨明明
杨明明, 邵 荃,丁 啸
(1.南京航空航天大学民航学院,南京 210016;2.上海农村商业银行总行,上海 201210)
时滞现象是引起系统振动和不稳定的关键因素,在工业过程、神经网络等实际生产生活中随处可见.近年来,许多学者对于时变时滞系统的区间显著性过程进行了大量的研究.He等[1]推动了最初的区间变时滞的发展,确定了基本的稳定性判据,并在文献[2]通过自由权矩阵方法,提出了有关区间时变时滞的神经网络更低保守性的研究成果.文献[3-7]使用的自由权矩阵方法和Jensen积分不等式对时滞系统稳定性进行进一步研究.文献[8-11]通过结合构造新的Lyapunov函数进一步改善了时滞系统的稳定性结论.彭丹和华长春[12]通过引入2-D Jensen不等式并结合Lyapunov函数给出了新的时滞系统稳定性准则.孙欣、高跃[13-14]将Writinger积分不等式应用于时滞系统,证明其与Jensen不等式相比有更低的保守性.
本文基于现有时滞系统的研究成果,通过将Jensen不等式转化为保守性更低的Wirtinger型不等式,并构建新的Lyapunov-Krasovskii泛函,结合自由权矩阵得到了基于线性矩阵不等式形式(Linear matrix inequality,LMI)的时滞系统渐近稳定性的新判据并进行了证明.
1 基本概念
1.1 Jensen不等式
Jensen不等式是反映凸函数的基本不等式,对于任意常数矩阵M∈Rm×m,M=MT>0,标量γ>0,向量函数[0 ,γ]→Rm有以下Jensen积分不等式:
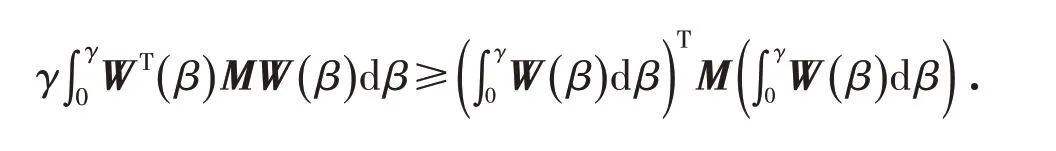
1.2 Wirtinger型不等式
与Jensen不等式相比,Wirtinger不等式的保守性更小[13].因此本文对Jensen不等式进行改进,得到新的Wirtinger型不等式.
Wirtinger不等式的形式为:对于任意常数矩阵M∈Rm×m,M=MT>0,向量函数[0 ,γ]→Rm有:
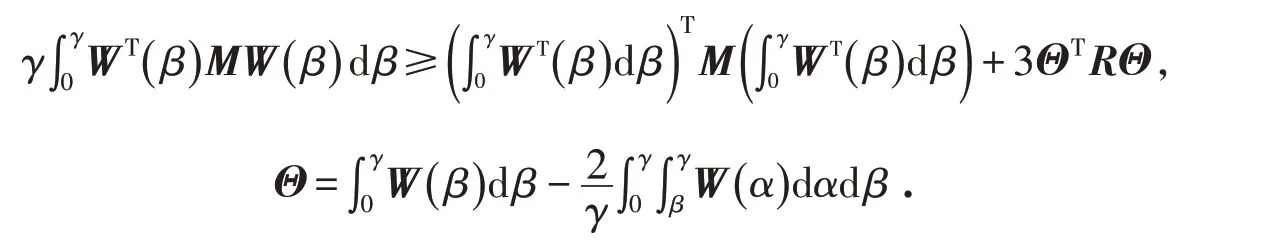
1.3 自由权矩阵
利用Park不等式或Moon不等式结合模型变换是解决时滞问题的主要方法,即在稳定性分析过程中用Leibniz-Newton公式来取代Lyapunov-Krasovskii泛函导数中的时滞项,即使用固定权矩阵来处理Leibniz-Newton公式间各项的关系,无法取代所有的时滞项,存在极大的局限性.
因此,为了克服固定权矩阵的保守性,自由权矩阵方法被引入用来表示Leibniz-Newton公式中各项的相互关系.通过求解LMI进行自由权矩阵优化,获得具有较低保守性的时滞相关稳定条件.自由权矩阵方法在处理Lyapunov-Krasovskii泛函导数时,不利用交叉项界定技术或模型变换,而是将ẋ(t)用系统方程ẋ(t)=Ax(t)+Ad x(t-h(t))替换后将该式左侧恒为零值的项加入Lyapunov-Krasovskii泛函导数中,从而得到时滞相关的稳定条件:
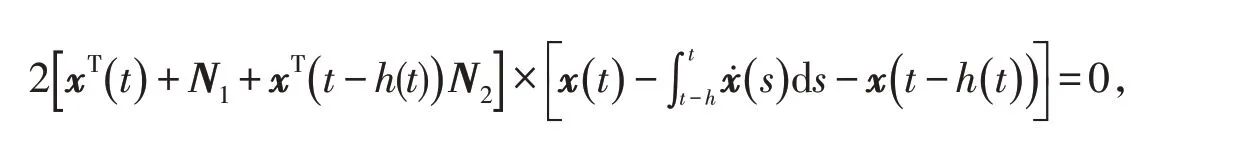
其中N1,N2是自由的,其最优值通过LMI的解求出,从而避免了固定权矩阵方法导致的高保守性.
2 稳定性分析
2.1 问题描述
考察以下中立型时滞系统:
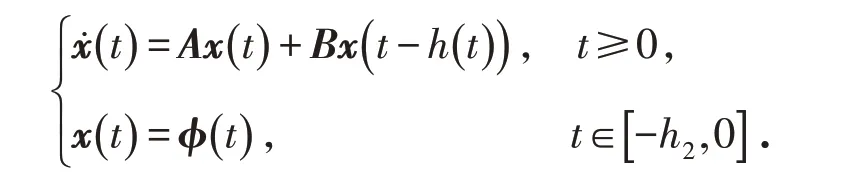
其中,x(t)∈Rn是系统状态向量,0≤h1≤h(t)≤h2,h12=h2-h1,且φ(t)∈C1(h2)为连续可微函数,定义域为[- 2h2,0].
2.2 改进的Jensen不等式
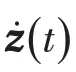
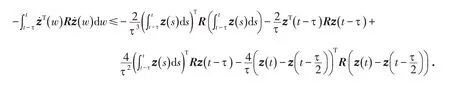
证明
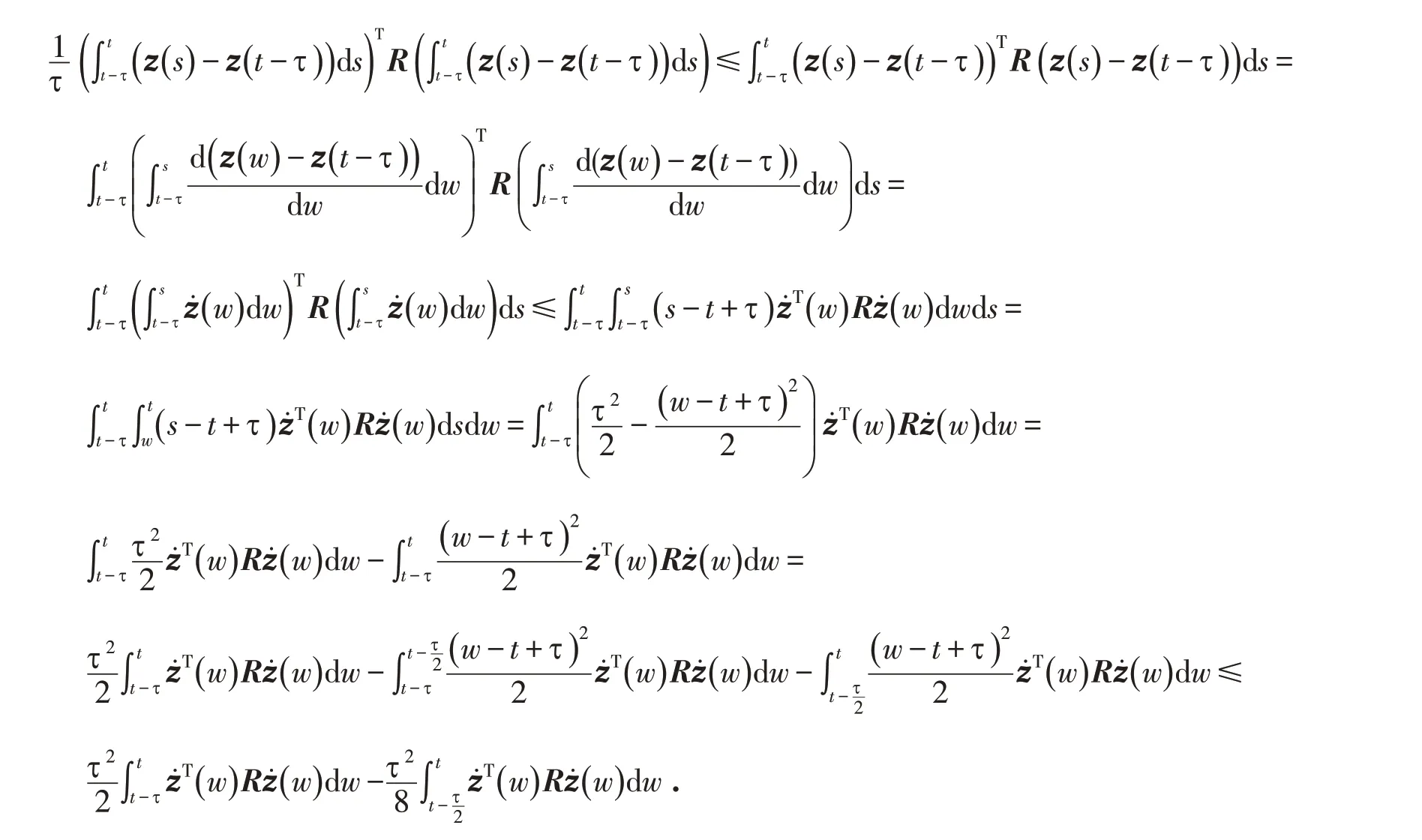
可以发现,
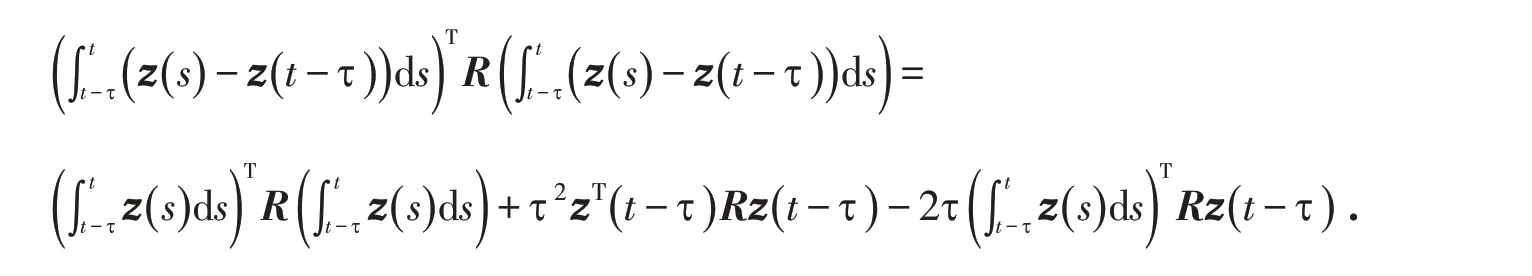
可推得:
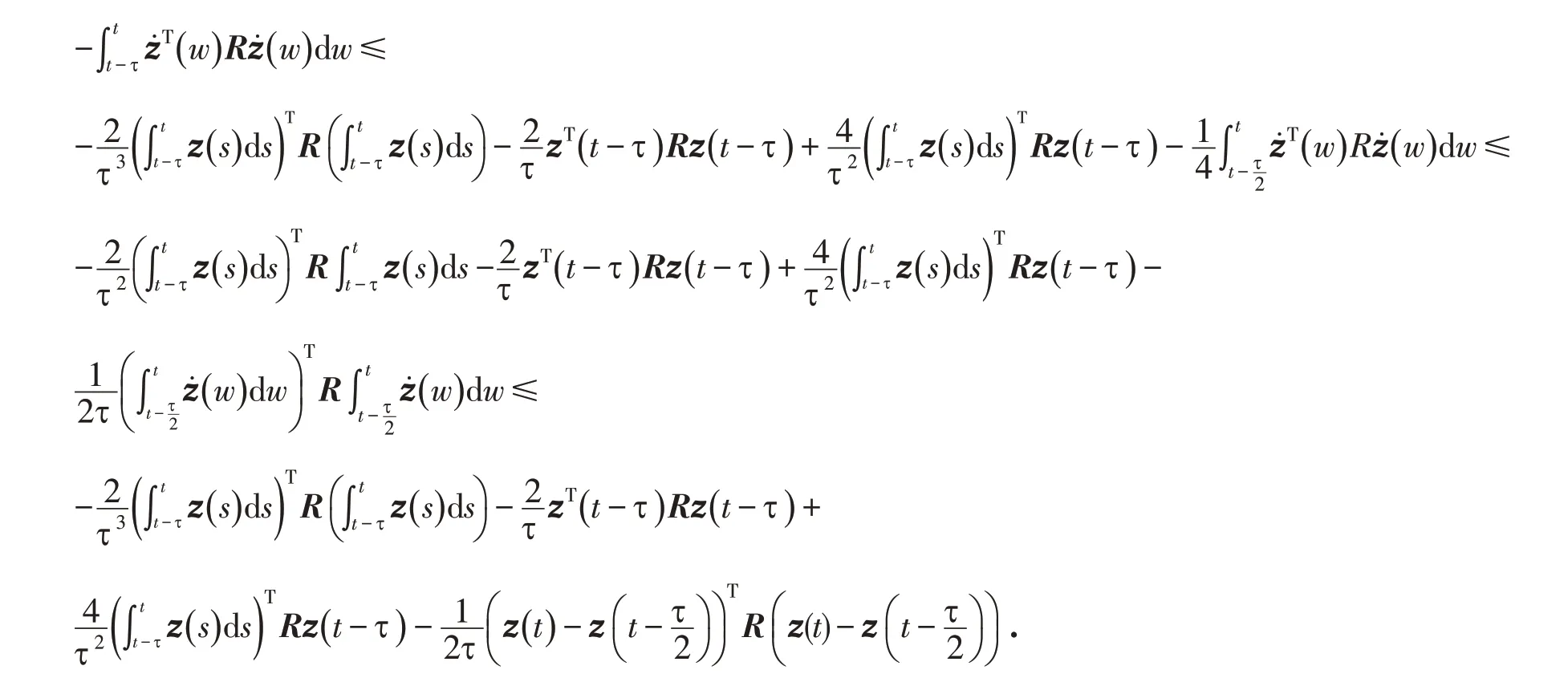
即定理1得证.
2.3 时滞系统的稳定性分析
做如下定义:
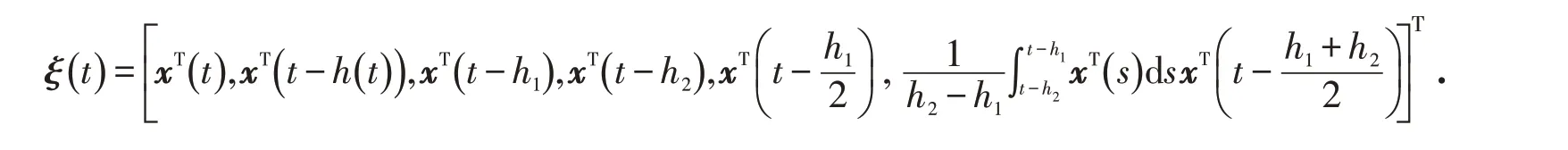
相应地分块矩阵如下:
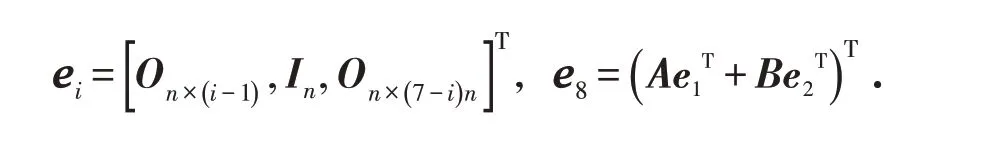
则该时滞系统可写作:
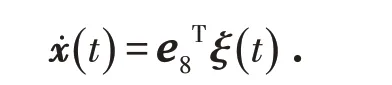
定理2 若存在矩阵P∈Rn×n,Q1∈Rn×n,Q2∈Rn×n,Q3∈Rn×n,R1∈Rn×n,R2∈Rn×n,满足线性矩阵Ξ<0,那么中立型时滞系统是渐进稳定的.
证明 构造如下的Lyapunov-Krasovskii泛函:
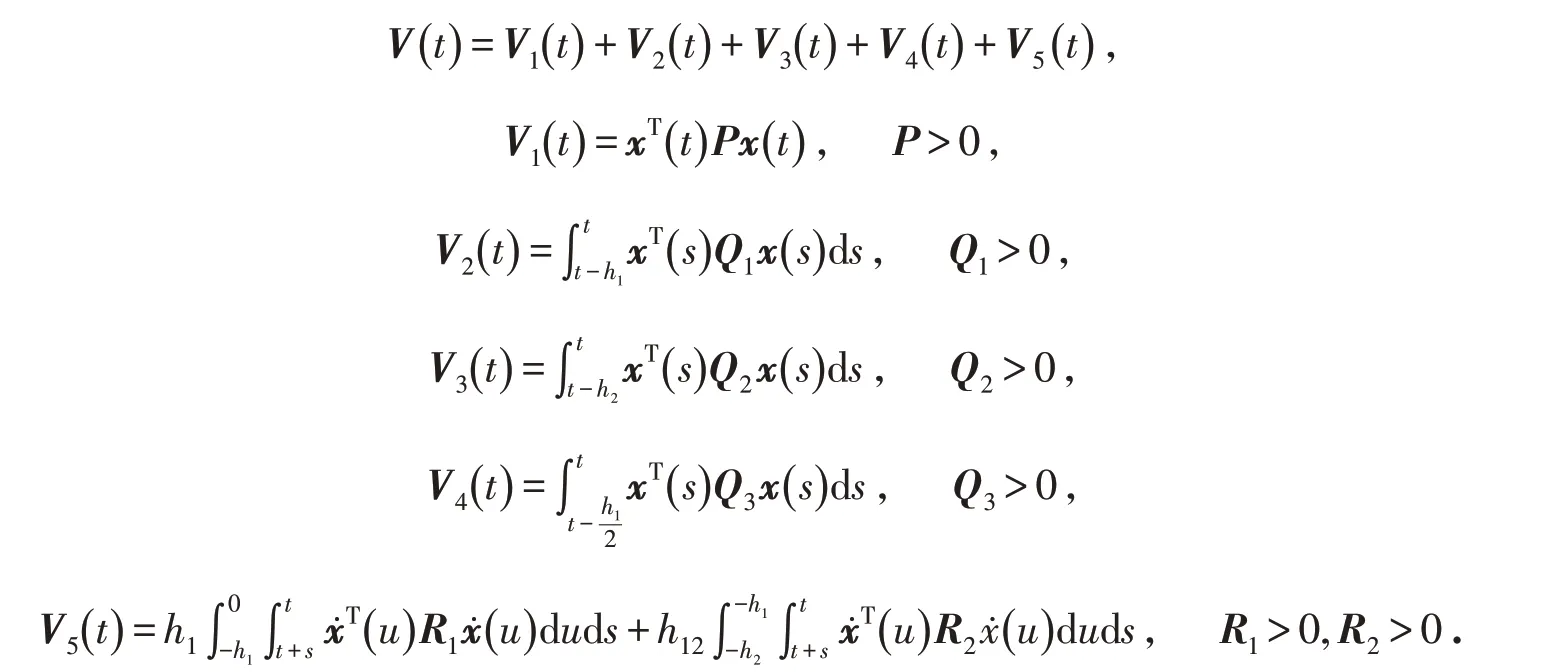
依次求导后可得:
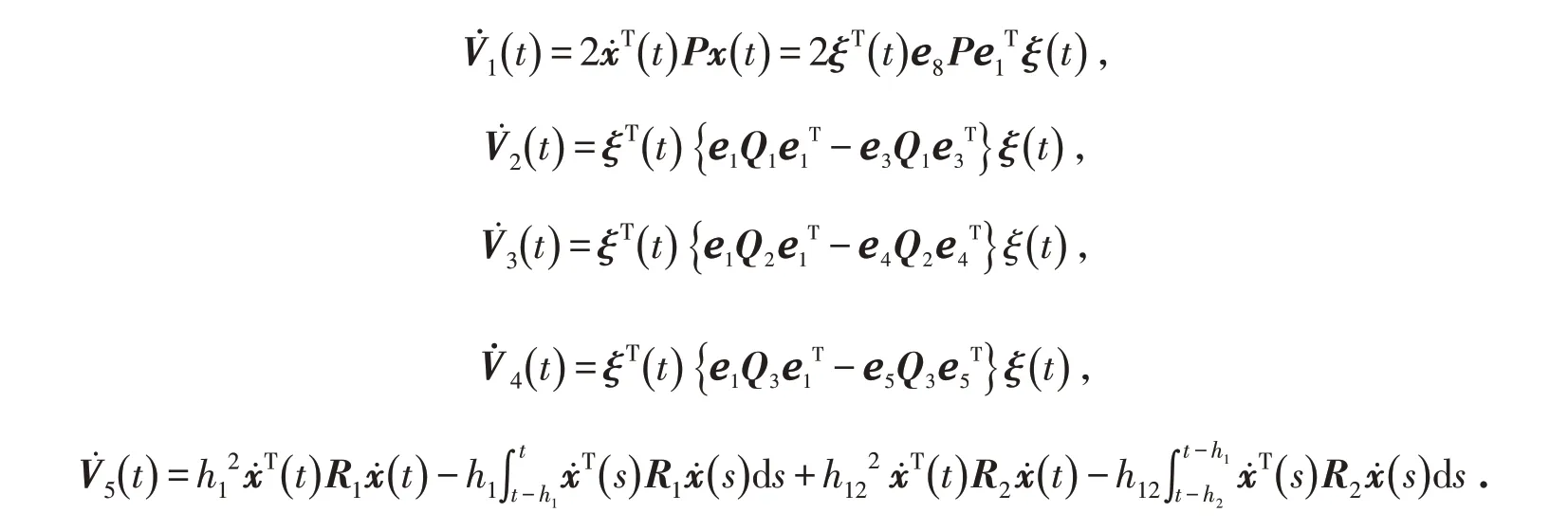
由定理1可推知:
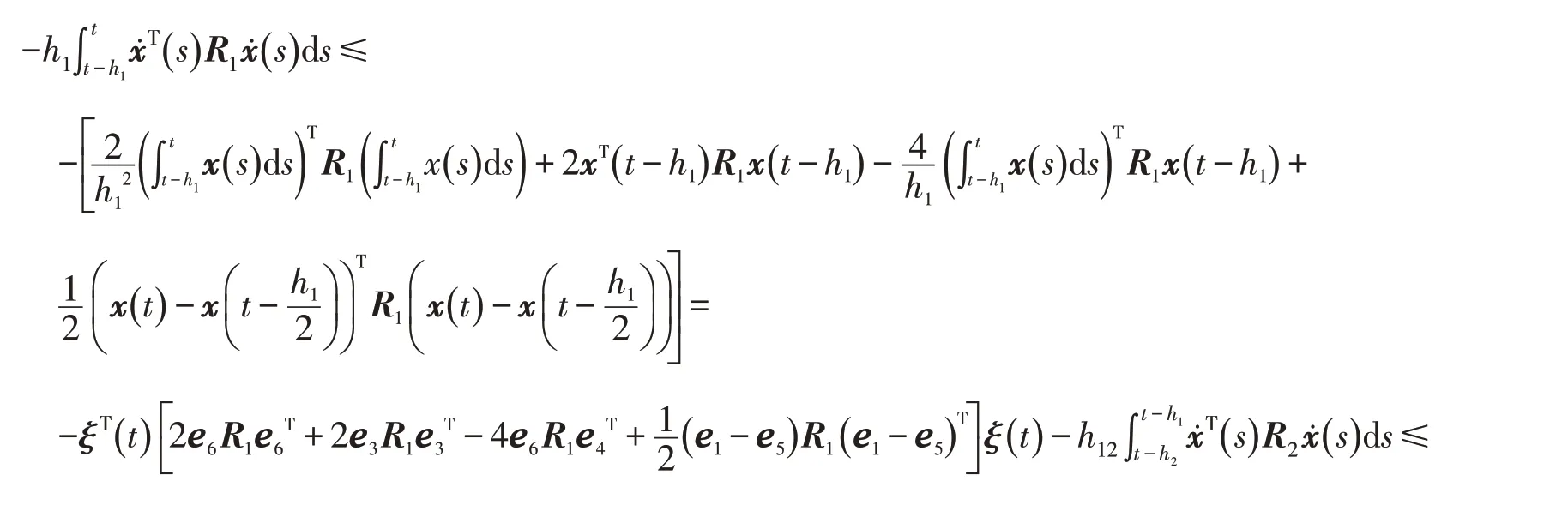
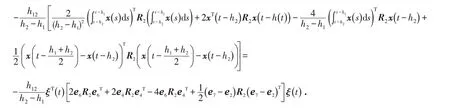
构造线形矩阵Ξ:

可得:
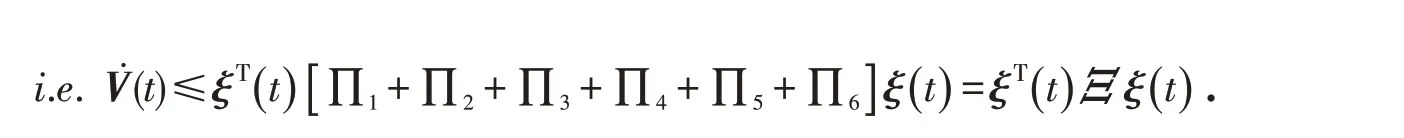
当Ξ<0时,V̇(t)<0,即时滞系统是渐进稳定的.
引入自由权矩阵,定义
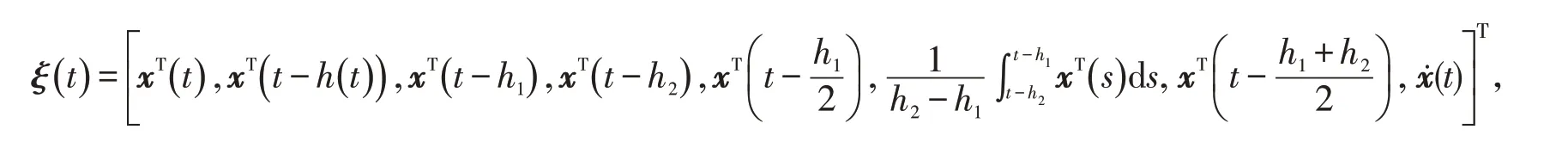
其相应的分块矩阵如下:

那么时滞系统有如下自由权不等式:
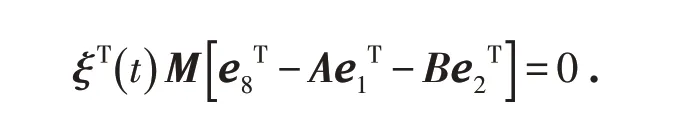
其中M为任意的合适维数的矩阵.结合该自由权不等式及定理2,可得定理3.
定理3 若存在矩阵P∈Rn×n,Q1∈Rn×n,Q2∈Rn×n,Q3∈Rn×n,R1∈Rn×n,R2∈Rn×n以及任意的M∈R8n×n,满足线性矩阵Ξ<0,时滞系统是渐进稳定的.
其中:

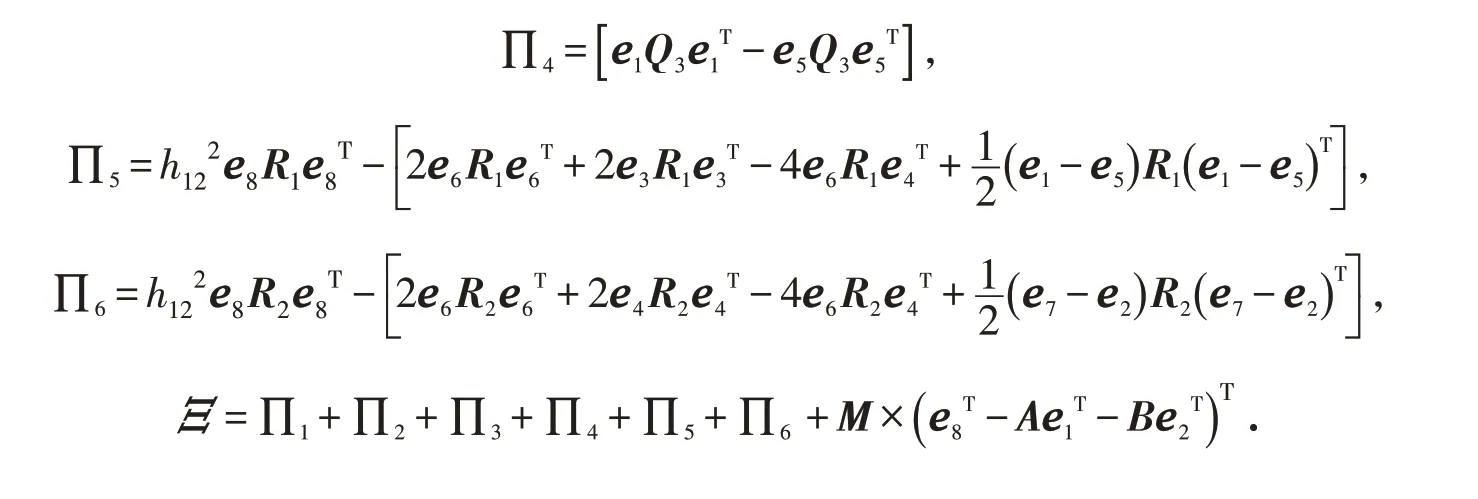
3 结论
本文以中立型时滞系统作为研究对象,将Jensen不等式进一步构建成为保守性更低的Wirtinger型积分不等式,利用Lyapunov第二方法构造新的Lyapunov-Krasovskii泛函,并引入自由权矩阵来表示Leibniz-Newton公式中各项之间的关系,最终得到了保守性更低的时滞系统稳定性判据.
