利用同构求解圆锥曲线问题*

广东省中山市中山纪念中学(528454)李文东

数学中的同构式是指除了变量不同,而结构相同的两个表达式.数学中的同构式,它不仅体现了数学的对称和谐美,而且运用同构式的思想解题能够培养学生的抽象,转化化归的思维能力.例如求数列的通项公式的关键就是将递推公式变形为“依序同构”的特征,即关于(an,n)与(an-1,n−1)的同构式,从而将同构式设为辅助数列便于求解.在解析几何中,经常碰到结构相同的问题,此时我们如果采用同构的思想来处理,会给我们的解题带来很大的方便,下面举例说明.

一、过曲线上一定点的两直线的斜率同构

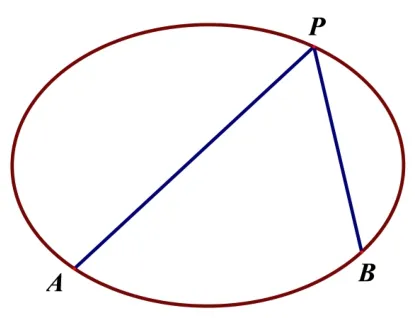
图1

代入曲线C的方程可得关于k1的一元二次方程同理可知k2也满足该方程,即k1,k2是方程aK2+bK+c=0 的两根,利用这个方程可以方便的处理与直线PA,PB的斜率之和或之积问题.

二、过曲线外一定点的两切线同构

1 过曲线外一定点的两切线的斜率同构

过曲线C外一定点P(x0,y0)作曲线C的切线PA,PB,切点分别为A,B,设直线PA,PB的方程分别为:y−y0=k1(x−x0)和y−y0=k2(x−x0),联立y−y0=k1(x−x0)与曲线C的方程,根据相切得Δ=0或d=r(曲线为圆时)得到关于k1的一元二次方程同理可知k2也满足该方程,即k1,k2是方程aK2+bK+c=0 的两根.

例3如图 2,已知M(x0,y0)是椭圆上的任一点,从原点O向圆M:(x−x0)2+(y−y0)2=2 作两条切线,分别交椭圆于点P、Q.若直线OP,OQ的斜率存在,并记为k1,k2,求证:k1·k2为定值.

图2

2 过一定点的两切线的切点方程同构

三、参数同构