基于数学文化浸润的章头引言课教学
2021-08-10叶良铨


摘 要:高考评价体系指出“要将立德树人融入考试评价全过程,健全立德树人落实机制”.数学文化对学生形成正确价值观、数学观有不可或缺的作用,而教材中的章头引言引领着全章,蕴含着丰富的数学精神、数学史、思想和方法,因此充分认识章头引言的作用,选择恰当的教学策略,浸润数学文化,是目前课堂教学迫切的价值追求.
关键词:章头引言;数学文化;教学策略
引言
李大潜院士曾提出:“数学是一种先进的文化,是人类文明的重要基础.它的产生和发展在人类文明的进程中起着重要的推动作用,占有举足轻重的地位.”[ 1 ].教育部在2003年颁布的《普通高中数学课程标准》(实验)中,在标题中首次使用了“数学文化”一词,并在四个位置用大量的文字从数学文化的角度来阐述观点,这标志着数学文化走进了中小学课堂[ 2 ].
现行人教A版2020普通高中新教材在它的每一章的开篇部分都安排了几段简明扼要的文字说明,它是全章内容的导入材料,引领全章,是每一章知识的生长点和着眼点,引领着全章起始课的教学,称为“章头引言”.章头引言位于每一章的起始位置,让学生了解本章的学习背景、意义和必要性,提升学习的欲望,同时让学生对本章学习的内容有个大致的了解,它以数学的眼光概述了与本章内容相关的数学史、人文价值、数学精神,从而浸润数学文化,培养学生的探究、求真的数学精神,激发学生学习的热情和欲望.
1 基于数学文化浸润的章头引言课教学的价值
1.1 挖掘章头引言所蕴含的数学文化,上好数学概念课
数学史是数学文化的一部分,在高中数学概念的引入环节,教师可以以数学文化创设情境,引领学生了解数学概念的发展历程,知晓概念的背景,领会数学知识的本源,激发学生的求知欲和探究心理.
例如,在高中数学新教材必修第二册第七章讲授“复数”概念时,可以充分地利用章头引言,引导学生一起学习以下数学史,以时间轴为主线,创设教学情境,还原“复数”的前世今生.
复数是在解方程的实践过程中解出来的.1545年,数学家卡丹(G.Cardano)在研究开篇那道题时,他给出了一种答案:
提出了卡丹公式,他将这类数称之为“诡辩量”,同时他是历史上第一个将负数的平方根写入算式中的人.1637年,法国哲数学家笛卡儿将这类数命名为“虚数(imaginary) ”也就是想象中的数.1777 年,瑞士数学家欧拉用 “i” 符号来表示虚数.发表了对复数的发展具有重要意义的欧拉公式:
eix=cosx+i·sinx
欧拉用这个公式处理了大量数学问题.
1799年,维塞尔首次发表了对复数的正确几何解释并把复数表示为平面向量.1830年,高斯第一次发表了有关复数几何表示的论文,并详细论述了用直角坐标系上复平面上的點表示复数a+bi,使复数有了立足之地,人们才最终承认了复数.
在数学史上,虚数以及复数发展过程,饱含着数学家的辛勤汗水和坚忍不拔、精益求精的精神.倘若教师能带着学生一起重温这段历史,不仅可以让学生理解复数概念的源头,更能让学生感受到数学文化之精华,意义深远.
1.2 利用章头引言,渗透数学人文精神和辩证唯物主义 ,树立民族自豪感
教材中,不少“章头引言”都介绍了我国在这章节知识的成就,我们可以课前查找一些文献,通过图片展示、小视频、讲数学史引领学生学习了解国内、国外在这方面的成就.这不仅对于学生树立正确的人生观、价值观、数学观以及人文素养的培养有极大的帮助,同时也增强了民族自信、文化自信,更加坚定了中华民族伟大复兴的中国梦.
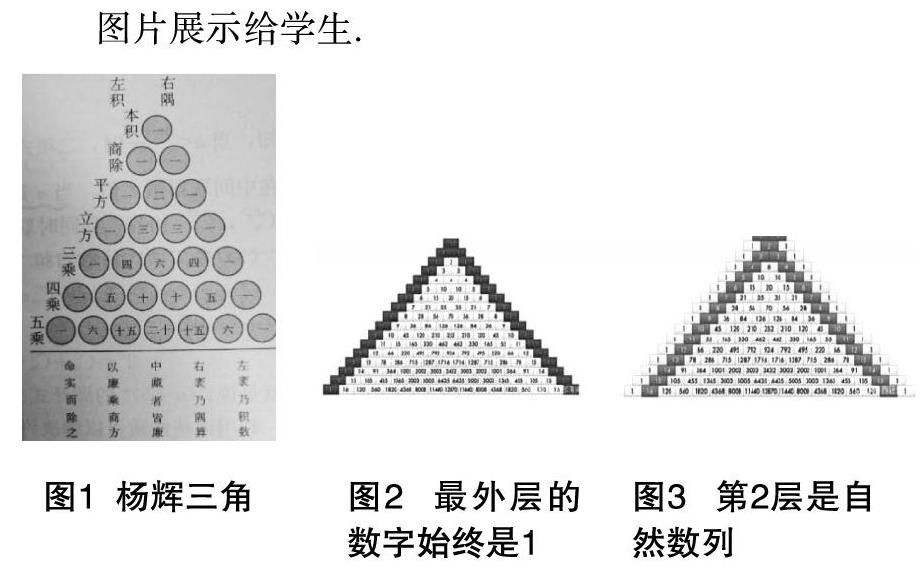
例如,在选择性必修第三册第六章章头引言课教学时,我们就可以利用这个阵地好好地介绍一下我国的杨辉三角如图1.杨辉三角,是二项式系数的一种等边三角形数阵排列,两腰都是1,如图2,在同一行中距离首末两端等距离的两个数相等;在相邻两行中,除1以外每一个数都等于它“肩上”两个数的和(Crn+1=Cr-1n+Crn)如图3,杨辉指出这个方法出于《释锁》算书.值得指出的是,这个表在我国南宋数学家杨辉于1261年所著的《详解九章算法》一书里就出现了,比欧洲的帕斯卡三角形早500年,这是非常值得中华民族自豪的.
图片展示给学生.
遵循由特殊到一般的原则,由教师引导学生从不同角度认识蕴含在杨辉三角间的几类美学因子----自然美、和谐美、形式美、奇异美、对称美、统一美.一方面为后面的数学探究---《杨辉三角的性质与应用》埋下铺垫.另一方面,我国历代数学家们艰苦卓绝、勇于探索创新的数学精神将会深深植入学生的脑海,影响他们的心灵深处.但到了近现代,我国数学的发展止步不前,严重落后于世界.这样让学生又要以辩证唯物主义的态度来认识世界,从而激励学生严谨治学,开放思想,追求数学真理为人类的发展与科技的进步而奋斗.
1.3 利用章头引言浸润数学求真精神,厚植爱国主义情怀
通过在章头引言课中展现数学家创造知识的历程,让学生感受数学家坚忍不拔的求真精神,创新精神和理性的爱国主义情怀.
例如,在上选择性必修第二册第五章的章头引言课时,我们可以向学生介绍微积分的发展历程,从精神上来更深远地浸润学生的心灵深处.
17世纪初,有四类问题束缚着人类社会的发展和科技的进步,这四类问题是:曲边梯形面积、曲线的切线、函数的最值、变速运动.几百年来,历代科学家们为了破解这些数学问题前赴后继,也得到了一些有建树的理论.直到17世纪中叶,英国物理学家牛顿和德国数学家菜布尼茨,凭着他们敏锐的直觉和丰富的想象力,在前人探索与研究的基础上,各自独立地创立了微积分.
在中国,刘徽在他所著的《九章算术》(公元263年)(图4)中的“割圆术”(图5):割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣.“割圆术”体现了极限思想,他是在人类历史上首次将极限和无穷小分割引入数学证明[ 3 ].
一个知识的创造史,就是古今中外历代数学家们艰辛卓绝的奋斗历程.他们在为世界奉献智慧、寻找数学答案的同时,他们的身上无一不绽放着勇于创新,不屈不挠的高尚品格,指引着历代数学工作者的前赴后继.作为新时代的一线教师应该责无旁贷地在课堂教学中浸润数学文化,传承数学家们优秀的求真精神和创造性精神,让学生润泽数学家们的高尚人格魅力.
2 结束语
叶澜教授说:“有文化意义的课堂,一定是充满生命激情、生命动感的课堂.课堂要凸现学生的主体地位,尊重学生的生命价值,发挥学生的主动性,赋予课堂教学以生命的意义,让课堂充满生命的活力 .”课程改革已经走进“一核四层四翼”的时代,数学文化更不是空中楼阁、虚无缥缈,它完全可以通过教师的挖掘实实在在地渗透到课堂中发挥其育人的潜在功能,让学生用数学的眼光去感受数学的深刻和优美,获得无形向上力量,为他们的终身发展奠基,为人类社会发展作出贡献.
参考文献:
[1] 李大潜. 将数学建模思想融入数学类主干课程[J]. 工程数学学报,2005,22(8).
[2] 中华人民共和国教育部. 普通高中数学课程标准[S]. 北京:人民教育出版社,2003.
[3] 叶良铨. 融入数学文化 实现学科育人[J].中学理科园地,2020(8).
