中立切换系统在异步切换下的指数稳定性
2021-08-10齐齐哈尔大学李明侠
齐齐哈尔大学 李明侠
切换系统是众多系统中特殊的一种动态系统,它是由有限个离散的或者连续的子系统和一个切换信号组成。这个切换信号是用来组织和协调这些子系统进行有序的切换。近几十年,切换系统在控制论中的应用越来越广泛[1-6]。时滞是切换系统中较常见的现象,因此在研究切换系统的稳定性问题时要将时滞考虑在内。
在现有的时滞系统稳定性条件中,根据是否依赖系统中时滞的大小,可以将稳定性条件分为时滞独立和时滞依赖两类[6]。其中时滞依赖稳定性条件具有更小的保守性。已有的文献中只规定了一个上界,但是这种规定在工程中不一定成立。在实际工程应用中,时滞可能会更大地超过这个上界,我们称之为大时滞。而较大时滞在系统中的出现往往导致系统不稳定,因此研究含有大时滞子系统的稳定性是非常必要的[7]。
另外,外部扰动也是减少建模与实际系统的误差的又一必要的因素。简言之,在切换系统的研究中,可以利用时滞和扰动来控制系统,可以提高系统的控制效率,进而降低保守性。文献[5]研究了一类中立切换系统的指数稳定性。异步控制指的是各个控制器间的切换滞后于系统模型,其主要原因是在实际操作中,控制器需要一定的时间去识别系统模型,进而产生了异步。
到目前为止,对于切换系统异步切换下镇定问题已经被广泛研究,但是对于含有大时变时滞的切换系统在异步切换下的研究还不够深入。文献[1]对于线性切换系统在异步切换下的稳定性问题进行了分析;文献[4]讨论了在异步切换下具有混合时滞的切换系统指数稳定性。基于上述现实,带有非线性扰动的时滞切换系统在异步切换下的指数稳定性受到越来越多的关注。
对于带有非线性扰动的时滞切换系统的稳定性分析虽然已经取得了一些成果,但是还不够深入和完善。因此,在此类系统的稳定性研究方面还需要更多的努力,才能更好的服务社会。本文通过构造李雅普诺夫克拉索夫斯基函数,运用Jessen不等式和平均驻留时间方法,以线性矩阵不等式的形式,分别给出了大时滞系统在控制器匹配和不匹配的情况下系统指数稳定的充分条件。
1 问题描述
考虑如下非线性中立切换系统:

其中,x(t)∈Rn是状态向量;u(t)∈Rn是控制输入;A1i、A2i、Ci、Di是已知的适当维数矩阵;σ(t):0,∞→M={1,2,…,l}为切换信号;时变时滞d(t)和h(t)满足下式:0≤d1 构造一个无记忆状态反馈控制器式(2):u(t)=Kσ′(t)x(t),这里,{(t0,σ(t0)),(t1+Δ1,σ(t1)),…,(tk+Δk,σ(tk)),…}延迟时间Δk≤Γ。由式(2)闭环式(1)系统简化为:0≤h1≤h(t)≤h2<∞, 引理1:对于正定对称矩阵M∈Rn×n和常量γ>0,如果存在一个向量函ω:[0,r]→Rn,则下列不等式成立:。 对于给定常数α>0,β>0,i,j∈M,i≠j,如果存在正定对称矩阵Pi,R1i,R2i,Q1i,Q2i满足下式: 这里: 则异步切换下系统指数稳定。 t∈[tk-1+Δk-1,tk)和t∈[tk,tk+Δk)的情形。 2.2.1 当t∈[tk-1+Δk-1,tk)时,构造lyapunov函数 在此区间内,σ′(t)=σ(t)=i,对V1i(t)求导并结合0≤d1 由引理1得: 2.2.2 当t∈[tk,tk+Δk)时,构造lyapunov函数 在此区间内,σ′(t)=σ(t)=j,对V1i(t)求导并结合0≤d1 由引理1得: 同理,当t∈[tk+Δk,tk+1)时,我们有: 这里: 因此: 系统(1)指数稳定。 近些年切换系统仍然备受关注,而稳定性作为系统的一个重要特性,仍是系统研究的一个热点问题。由于时代的发展和科技的进步,系统模型的复杂程度日益增高,对所研究问题的精确程度也越来越高。控制器在系统的稳定性研究中起着非常重要的作用,而子系统与控制器的匹配要花费一定的时间,因此控制器之间的切换往往滞后于子系统之间的切换,进而引发异步切换问题。到目前为止,切换系统的镇定问题已经得到了广泛的研究。 本文研究了一类非线性中立切换系统在异步切换下的指数稳定性,通过选取适当的李雅普诺夫—克拉索夫斯基函数,运用平均驻留时间方法和积分不等式,在已有文献的基础上得到了更为复杂的非线性中立切换系统在异步切换下系统指数稳定的条件。 切换系统依然有许多问题函待解决,本文所讨论的对于含有非线性扰动的时滞切换系统的研究只是初步的,还有许多问题需要进一步研究:离散的非线性时滞切换系统的相关问题。本文所研究的系统是连续的切换系统,未对离散的切换系统加以讨论。日后会对离散的非线性切换系统的稳定性问题加以分析;理论联系实际。由于切换系统的稳定性问题与实际问题的联系非常紧密,若此类问题的研究仅限于理论的研究是远远不够的,如何将切换系统的稳定性理论应用于实际问题并将所研究理论服务于实际问题是今后值得深入研究的;在今后的研究中会在理论的基础上加入仿真,以更清晰地说明文章的结论的正确性。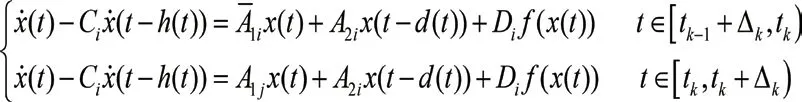
2 主要结果
2.1定理1
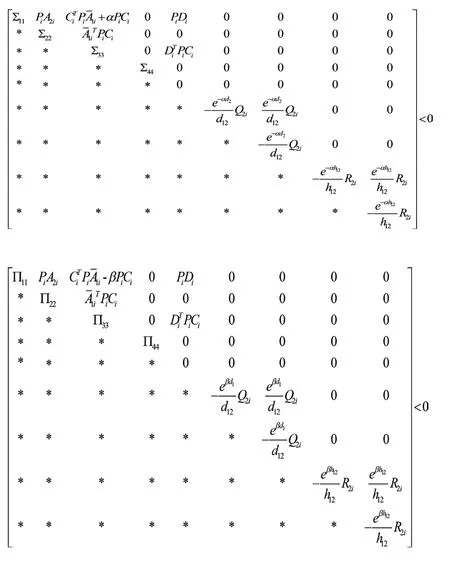
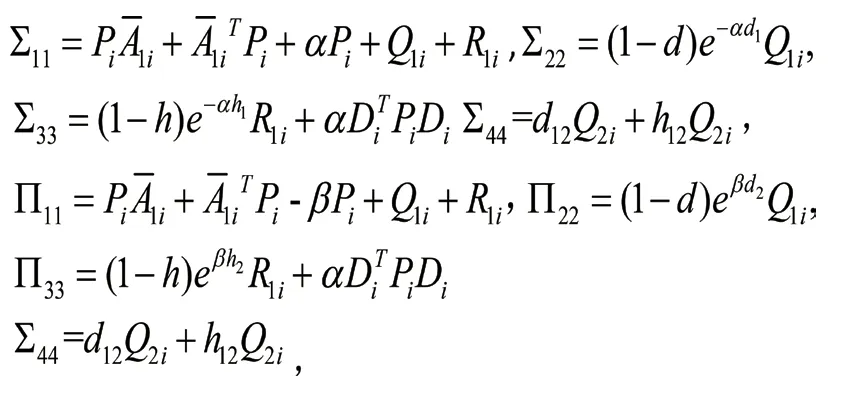
2.2证明
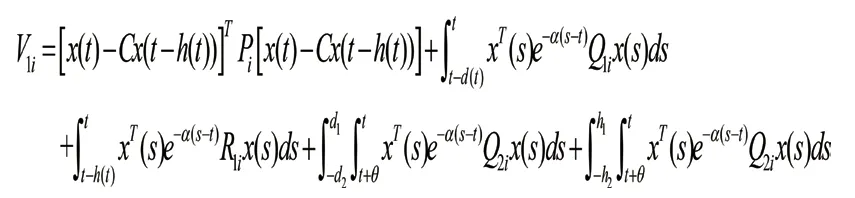
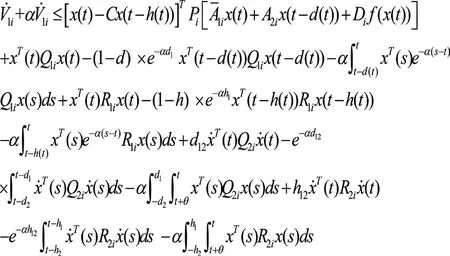
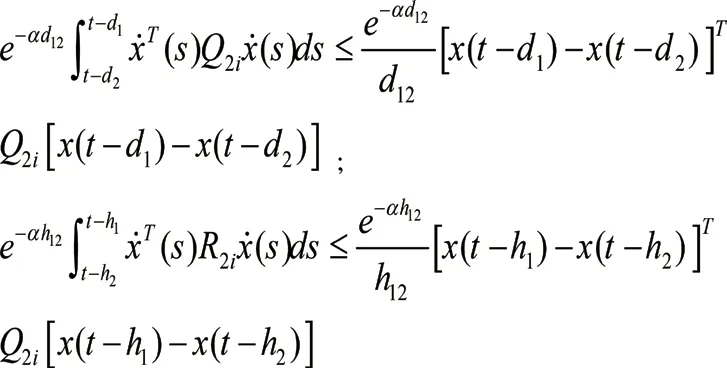
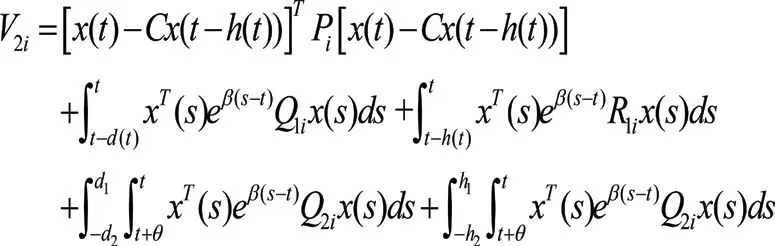
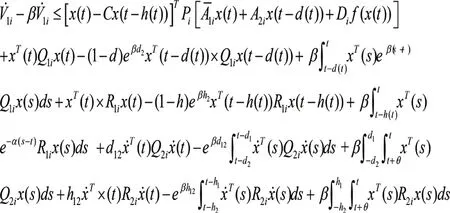
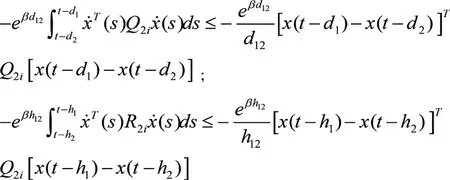
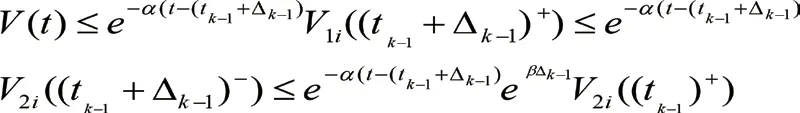
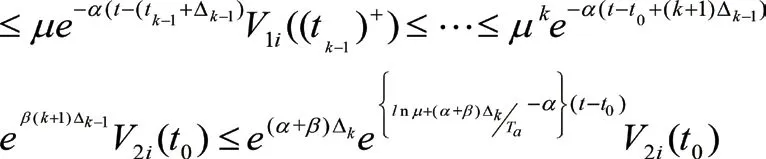
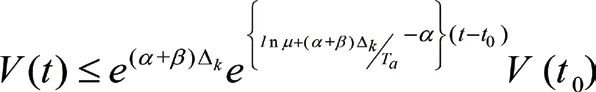

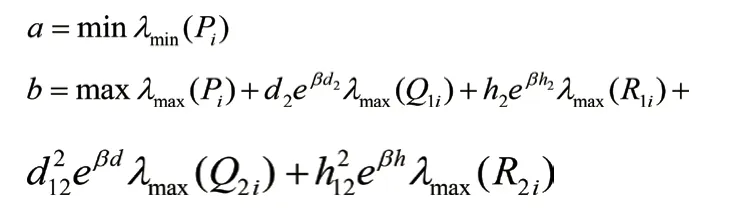
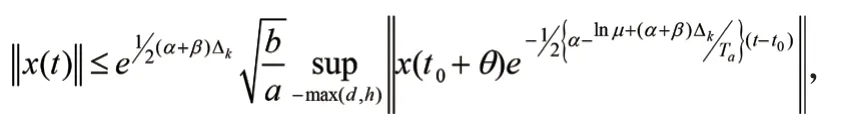
3 结语
