把握度量本质 拓展小数意义

[摘 要]度量是连接数量关系和空间形式的桥梁，也是人类认识、理解和表达现实世界的重要工具。在“小数的认识”教学中，教师要把握度量本质，让学生经历数数的过程，体会小数是由小数计数单位累加而成的，从而加深学生对小数意义的理解。

[关键词]度量本质;小数意义;计数单位

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）20-0072-02

一、课前慎思

1.对“度量”的认识

度量是用统一的度量单位去测量，其核心要素是度量对象、度量单位和度量值。度量的本质就是看度量对象中包含多少个度量单位。根据度量单位的不同分为抽象度量和具象度量。抽象度量是用计数单位去数数，着重于培养学生的数感;具象度量是用计量单位去测量，着重于培养学生的量感。

2.对“数概念”的理解

多与少是数量之间最基本的关系，与此对应，大与小就是数之间最基本的关系。基于数学本质的思考，数量的多与少或是数的大与小，就是抽象度量的本质。

整数可以一个一個、一十一十……地累加;分数可以八分之一、八分之二、八分之三……地累加;小数也可以0.1、0.2、0.3……地累加。无论是整数、分数，还是小数，它们都是计数单位的累加。

3.教材解读

关于“小数的认识”，教材分成了两个阶段。第一阶段是借助熟悉的元、角、分和米、分米、厘米初步认识小数，并不涉及计数单位和数位;第二阶段是借助实例，在小数与十进分数之间建立联系，抽象出小数的计数单位和数位，完善数位顺序表，拓展小数的意义。

如北师大版教材四年级下册第一单元“小数的意义（一）”中设计了三个活动：一是借助元、角、分等素材引导学生认识小数与十进分数的联系;二是抽象出一般意义上的小数与十进分数的联系，借助面积模型让学生理解小数的意义;三是通过生活中小数的实例来使学生加深对小数意义的理解。

二、课堂实践

1.动手测量，体会小数产生

（1）估一估：出示一根绳子，让学生估一估它的长度。（大约1米）

（2）量一量：让学生动手测量绳子的长度。（绳长90厘米）

（3）说一说：你发现了什么？（用米作单位去量，不能得到整数结果）

（4）小结：在测量时，不能正好得到整数结果，需要用小数来表示。

（5）拓展：教师介绍小数的历史。

【反思】

学生通过估、量、说的实践活动，明白了在实际测量和均分过程中得不到整数结果时需要用小数来表示，体会到小数存在的必要性。

2.联系生活，激活已有经验

（1）互学：自主思考，同伴交流。

0.5元是什么意思？和1元有什么关系？

0.9米是什么意思？和1米有什么关系？

（2）群学：分享理解，展示思维。

生1：0.5元是5角。因为1元=10角，把1元平均分成10份，1角占1元的1/10，就是1/10元，也是0.1元。5角占1元的5/10，就是5/10元，也是0.5元。

生2：0.9米表示9分米。因为1米=10分米，把1米平均分成10份，1分米占1米的1/10，就是1/10米，也是0.1米。9分米占1米的9/10，就是9/10米，也是 0.9 米。

（3）共学：借助直观，加深理解。

课件出示元、角的人民币模型和线段图，动态演示0.5元与1元、0.9米与1米的关系，并总结：0.5元就是5/10元，0.9米就是9/10米。

【反思】

从生活经验入手，利用“元、角、分”或“米、分米、厘米”等模型，让学生初步感知分数与一位小数的联系，为拓展小数的意义奠定基础。

3.借助直观，拓展小数意义

（1）在直观中认识一位小数。

师：0.6表示什么意思？请你想办法表示出来，可以画一画、写一写。

（学生自主探究、小组交流后汇报）

生（齐）：0.6表示把1平均分成10份，取其中的6份，也就是6/10。

用面积模型和线段图表示如下：

总结：把1平均分成10份，其中的1份用1/10表示，也可以用0.1表示;6份就是有6个1/10（0.1），可以用6/10表示，也可以用0.6表示。

师：我们把像0.1、0.2、0.3……这样的小数叫作一位小数。这些一位小数中，你认为哪个最重要？为什么？

生3：0.1最重要，因为0.2是由2个0.1组成的，0.3是由3个0.1组成的……

【反思】

学生利用面积模型与线段图展示一位小数，体会0.6就是由“0.1”这个计数单位累加而成的，在建立一位小数与0.1关系的过程中体会计数单位的价值。

（2）在冲突中引出两位小数。

师：比0.6多一些，但又比0.7小，还能用0.6表示吗？该用多少来表示呢？和同伴说一说。

（学生独立探究、小组交流后汇报）

生4：把每个长方形平均分成10份，这样就把整个大正方形平均分成了100份，涂色部分有63份，占整个大正方形的63/100，用0.63表示。

师：把1平均分成100份，每份是1/100，可以用0.01表示;9份是9/100，可以用0.09表示;63份是63/100，可以用0.63表示。像 0.01、0.09、0.63……这样的小数叫作两位小数。

师：0.01和0.63又在这条线段上的哪里呢？请找一找。

（课件出示线段图（略））

师：哪个数是两位小数的基础？为什么？

生5：0.01。因为0.09是由9个0.01组成的，0.63是由63个0.01组成的……

【反思】

“比0.6多一些，但又比0.7小，还能用0.6表示吗？”这个问题让学生产生认知冲突，学生借助模型进一步细化单位，引出两位小数的计数单位“0.01”，通过数数，体会两位小数就是由若干个0.01累加起来的，并通过在线段图上找两位小数，培养数感。

（3）在联想中引出三位小数。

师：0.663又在哪里呢？在图上找一找。

学生借助已有经验进行联想，通过推理得出：再把面积模型中的每一长条都平均分成100份，这样整个面积模型就被平均分成了1000份，涂色部分有663份，占整体的663/1000，可以用0.663表示，同时还可以在图上找到其他三位小数。

【反思】

教师继续制造认知冲突，用问题引领学生思考，使学生在联想、推理中认识三位小数，借助直观模型在经历不断细分分数单位的过程中拓展小数的意义。

（4）沟通联系，深化计数单位。

师：0.1、0.01、0.001……是小数中的重要成员，它们对认识小数格外重要，我们称它们为计数单位。

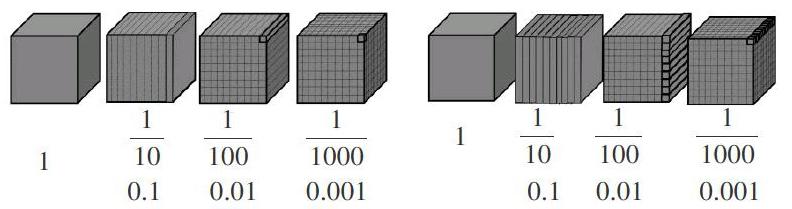
师：把1个正方体木块平均分成10份，每一份是多少？繼续分，平均分成100份，每一份是多少？接着分，平均分成1000份，每一份是多少？还能继续分吗？

师：观察，你发现了什么？

生（齐）：10个0.001就是0.01;10个0.01就是0.1;10个0.1就是1。相邻两个计数单位间的进率是10。

关于数的认识，从整数的认识，到小数、分数的认识，再到负数的认识，就是“自左向右”的数级拓展，“向微观”的数域拓展，“自右向左”的改变方向，但本质都是计数单位的累加。数起源于数，量产生于量。在数的认识教学中，教师要让学生尽情地数数，系统地数，不断感受度量的价值，体会数的本质。

[ 参 考 文 献 ]

[1] 黄慧章，郑大明.基于度量本质的教材解读与教学探究[J].小学教学参考，2020（2）.

[2] 娜仁格日乐，史宁中.度量单位的本质及小学数学教学[J].数学教育学报，2018，27（06）.

（责编 黄 露）