弄通小数乘法的理:从为什么越乘越小说起
2021-08-09郭慧
郭慧

[摘 要]针对学生的小数乘除法运算正确率低的现象,以小数乘法教学为例,展现教学关键过程,分析引发学生错误的原因,提出沟通整数除法与小数除法算理的一致性,以及通过加强对小数意义的理解来促进学生对小数乘法算理的理解。
[关键词]小数乘法;教学改进;运算一致性;算理算法
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2021)20-0018-02
计算教学是小学数学教学的重要内容,虽然课程改革后的小学数学的教学内容比以前更丰富了,但计算依然是小学数学中比重较高的内容之一。相对整数的四则运算来说,小数的四则运算对学生来说有一定难度,尤其是小数的乘除法。笔者曾选择353名来自城市学校和农村学校的学生,以所用教材(北师大版教材)上的8道小数除法练习题作为测试题,结果能做对8道题的学生仅占31.1%。怎样才能提高小数乘除法运算的正确率?如果只是一味地增加练习题,可能短时间内会有提高,但从素养本位、能力为重的数学教学要求来看,这只能提高运算的技巧或运算的技能,并没有促进运算能力的提高以及数学素养的形成,显然不是一种理想教学的选择。那么,怎样实现学生从技能到能力的转变?本文将以“小数乘法”教学为例,谈谈怎样让学生既掌握算法,又弄通算理,从而提高理解能力和正确率。
一、教学现象再现
【教学片段1】四年级“小数乘法”第一课时
教师从整数乘法入手,依次给出4×2、40×2、400×2,引导学生观察这些算式的特点,并说说它们之间的规律;然后出示0.4×2、0.04×2,让学生思考后总结出“小数乘法可以先转化为整数乘法进行计算”,进而让学生思考:“积的变化规律在小数乘法中成立吗?你能用什么方法验证?”
学生反馈:
方法1: 0.4×2,就是2个0.4相加,即0.4+0.4=0.8。同理,0.04×2=0.08。
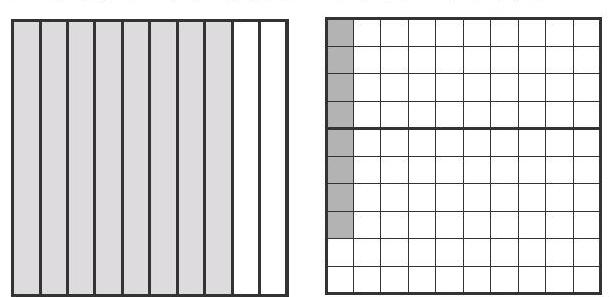
方法2:利用面积模型理解(如下图)。
从教学的整体情况来看,学生的学习都在教师的基本预设之中,进行得非常顺利。然而面对练习题“3×0.5”时,有一个学生举手提问:“不对呀,怎么会越乘越小呢?”
无独有偶,“怎么越乘越小了”这句话让笔者想起另一个课堂。
【教学片段2】四年级“积的小数位数与乘数小数位数的关系”(“小数乘法”第四课时)
教师先呈现一组信息“一张单人学生桌,长6分米、宽4分米,面积是多少平方米?”,然后请学生独立思考解决,鼓励学生用不同的方法。
生1:6 dm×4 dm=24 dm2=0.24 ㎡。
师:为什么24 dm2=0.24 ㎡?
生1:因为1 ㎡=100 dm2,24÷100=0.24(㎡)。
生2:6 dm=0.6 m,4 dm=0.4 m,0.6×0.4=2.4(㎡)。
(学生议论纷纷,有两种声音:0.6×0.4=2.4,0.6×0.4=0.24。原本很有信心的生2十分犹豫。)
生3(迫切地想表达自己的想法):我有一个问题,0.6×0.4不可能是0.24,怎么会越乘越小呢?因此不可能是0.24。
二、透过现象,分析成因
如果在小数乘法的第一课时,学生的质疑还是情有可原的话,那么在第四课时学生还提出“怎么会越乘越小的呢?”的疑问就让笔者深思……
整数乘法的算理是基于“几个几相加”,也就是乘法是加法的简便运算来理解的,即4×2是2个4相加,40×2是2个40相加。同理,出现 0.4×2时,学生自然而然想到是2个0.4相加。
学生已经通过前期的学习建立了这样的观念:乘法运算是累加的计算;乘法运算的积是累加的结果,自然是越加越多的……这些观念一直不断强化。因此,学生把整数乘法中 “越乘结果越大”的经验迁移到小数乘法中似乎是自然而然的。更何况,教师在教学中引导学生探索小数乘法的算法就是从整数乘法中一脉相承而来的。
史宁中教授指出:“人们一般认为,乘法是加法的简便运算,但事实上,问题并不这么简单。需要分两种情况讨论:一种情况是基于自然数集合的乘法,另一种情况是基于整数集合的乘法。”比如3×4,可以说是3个4或者4个3相加,但是-3×4则不能说是-3个4相加。根据这样的说法,小数0.3×0.4不能解释为0.4 个0.3或者0.3 个0.4相加。而学生一旦从整数乘法的意义上来理解小数乘以小数的乘法,就产生了“为什么越乘越小”的困惑。
那么,难道是整数乘法的算理不适用于小数乘法吗?作为整体教学的视角,教师应该重新审视整数乘法算理的教学。一个好的数学体系,不会因为数域的扩张,“理”就发生了改变,应该还是同一个“理”,这样学生学习起来才前后一致,融会贯通,所学知识才能起到“纲举目张”的作用。
在数的认识和运算中有两个重要的元素——数和计数单位,在整数乘法的算理教学中,重点落在数的计算上,而没有强调计数单位的运算,比如4×2=?,4个1与2个1相乘,4×2=8,1×1=1,8×1=8;同理,40×20=?,4个10与2个10相乘,4×2=8,10×10=100,8×100=800。如果按这样的算理进一步推导的话,小数乘法的“理”就相通了,0.4×0.2=?,4个0.1与2个0.1相乘,4×2=8,0.1×0.1=0.01,8×0.01=0.08。前后一致,算理相通。
三、整体设计,教学改进
【教学片段3】教学0.6×0.4
第一環节:删繁就简,意义理解得以真实发生
师(直接呈现算式,没有给出任何背景材料):0.6×0.4表示什么意思?
生1:表示0.4个0.6。
(生1一说出口就发现好像不对)
师:0.6表示什么意思呢?你能用图或者其他方式来说明0.6×0.4的意思吗 ?
(大部分学生选择了用面积模型表示,也有学生选择用文字表达)
生2: 0.6×0.4就是把0.6平均分成10份,取其中的4份。
生3:也可以说把0.4平均分成10份,取其中的6份。
生4:我知道了,我知道了!0.6×0.4是0.6里面的4/10,乘了反而少了!
生5:0.6×4就是2.4了!
师:我们也可以这样想,0.6×0.4=?,6个0.1与4个0.1相乘,6×4=24,0.1×0.1=0.01,24×0.01=0.24。
这个环节重在通过理解算式本身的意义推动学生以小数意义来理解小数乘法。因此,教师并不急于得出计算的结果,而是给予学生充足的时间自主探究、讨论交流,从而使得学生能够基于小数的意义来理解小数乘法的意义,并通过语言表达得以强化。同时,也使小数乘法从算理上与整数乘法保持一致。
第二环节:联系生活,算法算理真正融合
师(呈现教材“街心广场”的数学信息):地砖的长为0.3米,宽为0.2米,求出地砖的面积。请独立思考。
(许多学生都有意识地借助图形来解决问题)
生1:其实就是3×2=6,6个1/100。
师:为什么是6个1/100?
生1:一个大格是一平方米,就是100平方分米,那一个小格是1平方分米,现在有3×2=6个小格,就是6个1/100。
在这一环节中,学生联系生活经验理解算式在现实背景意义下的意义,算理与算法自然地融合。
四、教学反思,形成经验
学生产生“为什么越乘越小”的困惑的主要原因是整数乘法表示累加产生的负迁移。一方面,教师要努力让学生在理解整数乘法的算理的基础上,不为后续小数乘法留下不一致的思维印象;另一方面,追根溯源,把小数乘法建立在小数的意义的基础上,让学生真正理解小数乘法的算理,将数的认识与运算整合起来。学生在三年级“小数的初步认识”的学习就是建立在整数十进制位值及分数的初步认识基础上的,也就是说,学生已经初步建立了小数与分数的关系,感悟到小数与分数一样是“分”的结果,10×10=100,1/10×1/10=1/100,从这层意义上讲,引导学生从小数意义的角度来理解小数乘法算式本身的意义是完全可行的。
如果题目是“一块地砖长0.3米、宽0.2米,求出地砖面积”,几乎所有的学生都会把0.3米、0.2米转换成分米,也就是先把小数转换成整数再进行计算,然后通过面积单位之间的进率关系将结果转换成平方米。在这样的过程中,学生得到更多的是小数乘法算法的体验,并没有真正理解小数乘法的算理,学生对“为什么结果变小”还会心存疑惑。
史宁中教授认为:绝不可以简单地把算理理解为依附于运算的一种性质,而应当把算理理解为运算的本质。正因为这样,教师要加强运算的一致性,使得整数运算与小数运算在算理上保持一致,同时加强学生对数的意义的理解,将数的认识与运算联系起来,通过探究小数乘小数算式本身的意义,使得學生从小数意义本身理解小数乘法算理的本质内涵。只要理解对了,哪怕慢一点,计算错误也会大大减少。
(责编 金 铃)
