简谐振动冲击钻井技术破岩机制及钻进效果

2021-08-09李思琪田胜雷房永生

中国石油大学学报（自然科学版） 2021年4期

李思琪, 田胜雷, 李丽, 李玮, 陈卓, 房永生

(1.东北石油大学石油工程学院,黑龙江大庆 163318; 2.青海油田公司,甘肃敦煌 736202)

简谐振动冲击钻井技术是一项由阿伯丁大学应用动力学研究中心为提高质硬地层钻进效率而提出的一种新兴高效破岩方法[1-2],是一项配合以适当的钻压和转速,通过钻头向岩石施加周期性的简谐振动冲击而实现岩石破碎的一项钻井技术,当施加的激励频率与岩石的固有频率相等时,岩石产生共振,即为共振钻井。自该技术提出以来,已有许多学者针对其进行了大量研究[3-4]:一方面是关于冲击系统动力学特性的研究[5-7],通过建立钻柱系统的动力学模型分析冲击系统的运动状态和特性;一方面着手于室内试验测试[8-10],通过和常规钻井破岩试验对比,验证简谐振动冲击钻井技术的钻进效果。此外,还有少量研究针对该技术的破岩机制展开,主要分析了冲击特性参数[11-12]和岩石力学特性参数[13-14]对破岩效率的影响。和常规钻井技术相比,简谐振动冲击钻井技术相当于在静载(钻压)基础上对岩石介质施加了一个额外的周期性的动载(简谐冲击力),因此岩石介质在该动载作用下的响应情况也是研究简谐振动冲击钻井技术破岩机制的关键问题之一。笔者从岩石介质在简谐振动冲击下的响应问题出发,在已有的研究成果基础上[15],进一步考虑岩石介质的阻尼,完善简谐振动冲击下岩石介质的振动响应模型,分别推导岩石介质的位移和能量响应方程,最终从位移响应和能量响应两个角度解释说明简谐振动冲击钻井技术的破岩机制;然后通过开展简谐振动冲击钻进过程的模拟仿真,进一步分析该技术钻进过程特性;最后通过自主研发的轴向振荡冲击工具现场应用实例进一步验证简谐振动冲击钻井技术的提速效果。

1 简谐振动冲击破岩机制

1.1 物理模型

将钻头与岩石作用简化为平底压头与岩石的作用,用多个弹簧叠加模拟平底压头建立岩石介质振动模型,如图1所示。忽略弹簧间的耦合力,将压头下面的区域无限分割。由于平底压头与岩石介质作用面上压头各点对岩石的作用力相同,研究平底压头上一点与岩石介质平面上微元的作用关系即可代替整个平底压头与岩石介质的作用,因此单独提取一个小微元进行分析。假设岩石介质是各向同性的均匀介质,压头的简谐冲击力为F,冲击频率为ωi。由于重点考虑简谐动载的存在对钻头破岩的影响,虽然孔隙压力、液柱压力等其他因素也会对钻进过程产生不同程度影响,但并不会对结果的变化产生实质性的改变,因此分析过程中暂不考虑这些因素。

图1 压头冲击岩石简化模型

1.2 数学模型

在简谐力作用下,岩石会产生与静载作用不同的响应,这种响应直接决定着钻头的钻进效率,因此从岩石介质的位移响应和能量响应两个角度分析简谐振动冲击下钻头的破岩机制。

1.2.1 位移响应

外力作用下岩石介质的振动方程为

(1)

简谐振动冲击时压头施加的动载具有周期性,其冲击力为

F=fcos(ωit+β).

(2)

将式(2)代入式(1)得到其通解为

x=aexp(-λt)cos(ω1t+α)+b1cos(ωit+β+δ).

(3)

其中

式中,x为岩石的振动位移,m;ω为岩石的固有频率,rad/s;m为岩石质量,kg;f为冲击力的幅值,N;c为岩石阻尼,N·s/m;k为岩石刚度,N/m;ωi为冲击频率,rad/s;

式(3)即为考虑阻尼的岩石介质在简谐振动冲击下的位移响应方程。

1.2.2 能量响应

由哈密顿能量函数可知,在简谐振动冲击下,岩石介质的响应能量是只随时间变化的函数,与冲击系统所处的位置无关。

对于简谐振动冲击下岩石的一维振动模型,拉格朗日函数为

(4)

(5)

哈密顿能量函数则可写为

(6)

由于岩石介质处于微振动状态,基于得到的简谐振动冲击下岩石介质的振动响应方程,可以进一步得到

β+δ)+2a2λω1exp(-2λt)cos(ω1t+α)sin(ω1t+

α)+2ab1λωiexp(-λt)cos(ω1t+α)sin(ωit+

β+δ)+2ab1ω1ωiexp(-λt)sin(ω1t+α)sin(ωit+β+δ))],

(7)

α)cos(ωit+β+δ)],

(8)

β)+fb1cos(ωit+β+δ)cos(ωit+β).

(9)

将式(7)～(9)代入式(6)得

2a2λω1exp(-2λt)cos(ω1t+α)sin(ω1t+α)+

2ab1λωiexp(-λt)cos(ω1t+α)sin(ωit+β+δ)+

2ab1ω1ωiexp(-λt)sin(ω1t+α)sin(ωit+β+δ)]+

2ab1exp(-λt)cos(ω1t+α)cos(ωit+β+δ)]+

afexp(-λt)cos(ω1t+α)cos(ωit+β)+fb1cos(ωit+

β+δ)cos(ωit+β).

(10)

式(10)即为简谐动冲击下岩石介质的能量响应方程。

1.3 破岩机制

基于岩石介质的振动响应方程,可以得到岩石介质的位移响应曲线,如图2所示。

如图2所示,简谐振动冲击下岩石介质的位移响应也呈简谐形式波动,说明岩石介质会呈现上下往复的规律性振动。当压头以非共振频率冲击岩石时,即图2中的低频区和高频区,岩石介质的位移响应较微弱。当压头的冲击频率接近或达到岩石介质的共振频率时,即图2中的共振区域,很明显可以看到岩石介质的响应位移会达到峰值。

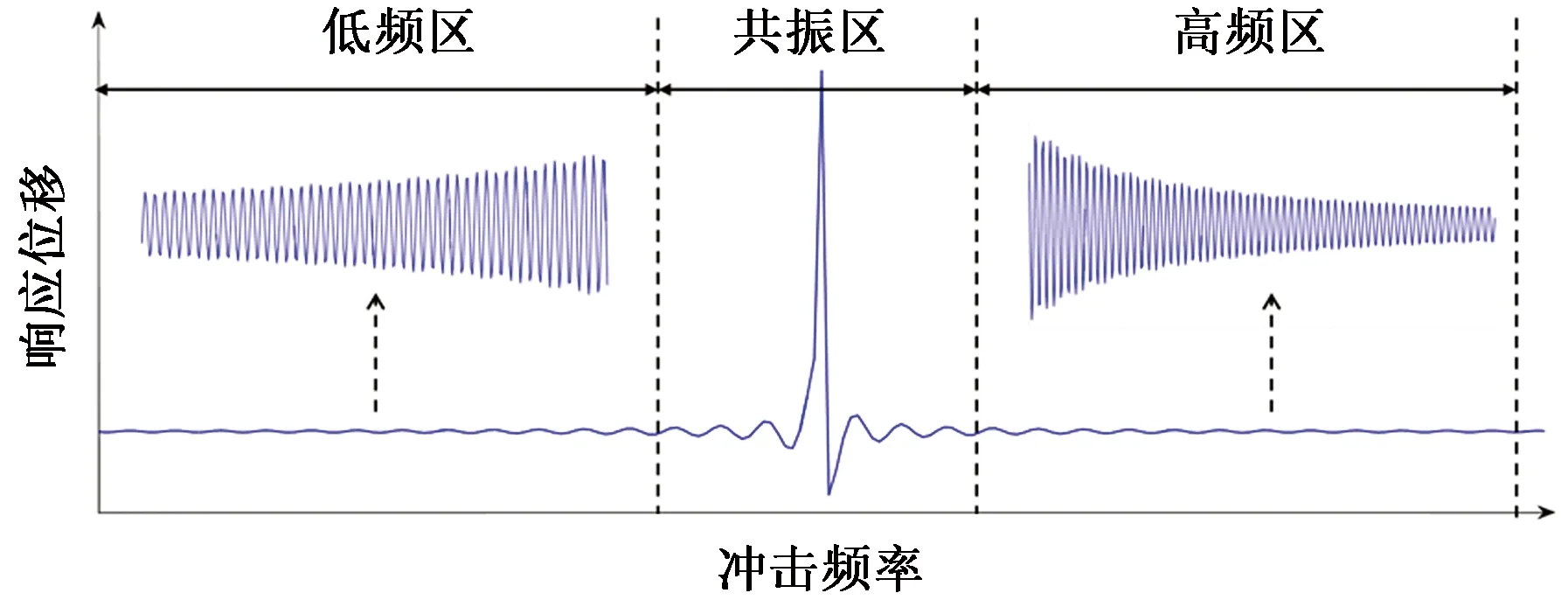
图2 不同冲击频率下岩石介质的位移响应

根据岩石介质的能量响应方程,可以得到简谐振动冲击下岩石介质的能量响应曲线,如图3所示。

由图3可以看出,简谐振动冲击下岩石介质的响应能量也以简谐波动形式进行规律性地衰减。当压头以非共振频率的简谐力冲击岩石时,岩石介质的能量响应波动强烈。当压头以共振频率的简谐力冲击岩石时,岩石介质响应能量达到稳定状态,此时岩石振动与冲击载荷保持相同步调,岩石介质最大程度吸收了压头的冲击能量用于自身运动状态的改变,冲击系统效率达到最优。

图3 岩石的响应能量随时间的变化曲线

总之,在简谐振动冲击下,岩石的规律性振动响应,无论是位移响应还是能量响应,均说明周期性的简谐冲击力对岩石介质产生了持续稳定地交变应力作用。该作用力使岩石介质在冲击载荷作用下,不仅单纯受到压应力作用,同时还会受到拉应力作用。由于岩石的抗拉强度远小于岩石的抗压强度,因此拉应力的存在使岩石更容易达到其抗拉断裂极限而产生断裂,从而使钻头破岩效率提高。另一方面由于施加的简谐力是高频的,在该载荷作用下岩石产生的简谐式振动响应会使其内部持续产生损伤累积,最终当总损伤量达到岩石疲劳破坏极限时,即使岩石受到的应力未达到其断裂极限也会发生破碎,这也是造成钻头钻进效率提高的一个原因。特别地,当简谐力的冲击频率与岩石介质的固有频率相同时,岩石达到共振状态,此时由于岩石介质的响应最为剧烈而更容易产生体积破碎。

2 简谐振动冲击钻进数值模拟

2.1 模型建立与求解

为进一步分析简谐振动冲击钻井技术的破岩效果和钻进过程,应用有限元软件动力分析模块对钻柱-钻头-岩石系统进行仿真模拟。为了更好地与钻井实际情况相匹配,建立的有限元模型包括了转盘、钻杆、底部钻具组合、钻头以及岩石等部件,如图4所示。具体模型尺寸设置如下:钻头采用Φ215.9 mm 5刀翼PDC钻头,设置为刚性单元;岩石岩性为石灰岩,尺寸为600 mm×600 mm×250 mm,考虑其弹塑性力学特性;底部钻具组合尺寸为Φ178 mm×500 mm,钻杆尺寸为Φ10 mm×1 000 mm,转盘尺寸为Φ400 mm×40 mm,均设置为弹性单元。

图4 冲击钻进系统有限元模型

为了提高求解精度,单元网格划分时分别将PDC钻头的切削齿部分以及钻头主要接触的岩石区域进行加密处理,从而保证网格划分的精细度已对结果不再产生影响。在载荷设置过程中,分别对转盘施加一个恒定的旋转角速度,对底部钻具组合施加一个恒定的钻压和一个简谐冲击动载。位移约束方面,对整体模型施加横向固定约束,在岩石底部施加全固定约束。此外,在PDC钻头表面中心位置设置一个刚性节点,用于读取钻头的轴向运动位移、运动速度、周向角速度、加速度等参数数据,从而进一步得到两种钻井条件下钻进效果对比结果。

模型中具体的钻井参数:转速为4.7 rad/s,钻压为15 kN,冲击力为7.5 kN,冲击频率为100 Hz;岩石特性参数:密度为2.75×10-9t/mm3,弹性模量为51 500 MPa,泊松比为0.33,屈服强度为120 MPa,摩擦角为30.16°,断裂应变为0.075。

2.2 结果分析

2.2.1 岩石主应力

图5为两种钻井形式下岩石最大主应力分布。图例中正号代表拉应力,负号代表压应力。相比于常规钻井,在简谐振动冲击下,钻头下会有更多的岩石单元受到拉应力的作用,这正是由于简谐振动冲击使岩石发生规律性简谐振动响应的结果。由于岩石抗拉强度又远小于抗压强度,所以岩石在简谐振动冲击下更容易产生破碎。

图5 岩石最大主应力分布

2.2.2 钻头轴向运动

常规钻井和简谐振动冲击钻井条件下钻头在轴向方向上的钻进特征如图6所示。

由图6(a)可以看出,由于钻头黏滑效应的存在,两种钻井条件下钻头的进尺均随着时间的增加呈阶梯状形式递增,但相同时间内简谐振动冲击下钻头进尺明显大于常规钻井,提高幅度达46.4%,说明简谐动载的存在确实可以实现提高钻井效率的目标。

图6(b)中常规钻井的最大机械钻速为39.59 mm/s,平均机械钻速为5.58 mm/s,简谐振动冲击钻井的最大机械钻速为54.77 mm/s,平均机械钻速为8.56 mm/s,平均机械钻速较常规钻井提高了46.3%,很明显可以看出简谐振动冲击作用显著提高了钻头轴向的钻进速度。此外,还可以得到常规钻井轴向最大的反向速度为15.94 mm/s,而简谐振动冲击下最大的反向速度为12.17 mm/s,且其轴向钻速的波动稳定性更优于常规钻井,说明简谐振动冲击钻井减缓了钻头的跳钻现象,改善了轴向钻进的稳定性。

图6 钻头进尺和机械钻速随时间的变化

2.2.3 钻头扭转运动

常规钻井和简谐振动冲击钻井在扭转方向上的运动特性如图7所示。

图7 钻头角速度和角加速度随时间的变化

和常规钻井相比,简谐振动冲击下钻头的旋转角速度略有下降,但下降幅度仅为3.4%。但从角速度变化的稳定性来看,常规钻井条件下角速度的标准方差为6.2,简谐振动冲击下角速度的标准方差为5.7,说明钻头的角速度变化更加稳定,这种稳定性主要体现在钻头的黏滞阶段,该阶段不仅被缩短了,而且钻头的反转现象也得到了明显的缓解。

从钻头旋转角加速度的角度看,也可以得到简谐振动冲击下的平均角加速度更高于常规钻井,角加速度的标准方差也更小于常规钻井的结论,这也进一步说明了简谐振动冲击钻井使钻头的切削作用更加有效、稳定。

3 应用实例

为实现简谐振动冲击钻井技术的现场应用并评价其钻进效果,东北石油大学高效钻井破岩技术研究室自主研发了轴向振荡冲击器。该工具的工作原理是将钻井液的流动转换成周期性的振动冲击传递给钻头,再由钻头将简谐力作用于井底岩石。将工作性能稳定的轴向振荡冲击工具应用于S井进行现场试验,如图8所示。工具的工作性能参数:井眼尺寸为241.3 mm、钻压为8～16 t、转速为50～70 r/min、流量为28～32 L/s、钻井液密度小于等于1.4 g/cm3。

图8 轴向振荡冲击器现场作业

S井现场试验的井段为3 970～4 220 m,其中3 970～4 140 m 井段使用的钻具组合为螺杆钻具+PDC钻头,4 140～4 220 m井段使用的是轴向振荡冲击器+PDC钻头的钻具组合。钻头在试验井段钻遇的岩性包括砾岩、泥岩以及粉砂岩,PDC钻头的机械钻速及钻遇不同岩性时的平均机械钻速随井深的变化如图9所示。

图9 S井试验井段钻速随井深的变化

在未使用轴向振荡冲击器时:PDC钻头钻遇1次砾岩层,平均机械钻速为1.42 m/h;钻遇4次泥岩层,平均机械钻速分别为2.22、1.94、2.31 及1.29 m/h;钻遇3次粉砂岩地层,平均机械钻速分别为1.68、1.72 及1.83 m/h。使用轴向振荡冲击器之后:PDC钻头钻遇粉砂岩层1次,平均机械钻速为1.95 m/h;泥岩层1次,平均机械钻速为2.04 m/h;砾岩层2次,平均机械钻速分别为1.52 和1.35 m/h。通过对比使用轴向振荡冲击器前后相同岩性机械钻速可得,砾岩层、泥岩层、粉砂岩层的平均机械钻速分别提高了1.44%、5.2%、12.1%。

众所周知,随着钻井深度的增加,地层压力逐渐增加,岩石强度随之提高,钻头磨损严重,机械钻速也随之下降。然而在本应用实例中,随着井深的增加,使用轴向振荡冲击器之后,钻头的机械钻速不但没有降低,反而针对不同岩性有了不同程度地提高。虽然钻速提高的幅度并不显著,这主要由于工具与钻井参数的匹配优化等客观原因,但已足以证明简谐振动冲击作用可以起到提高机械钻速的效果。