基于支持向量机和主成分分析的辫状河储层夹层识别

2021-08-09徐守余李顺明韩业明

中国石油大学学报（自然科学版） 2021年4期

陈修, 徐守余, 李顺明, 何辉, 刘健, 韩业明

(1.中国石油长庆油田勘探开发研究院,陕西西安 710018; 2.中国石油大学(华东)地球科学与技术学院,山东青岛 266580;3.中国石油勘探开发研究院,北京 100083; 4.中国石油集团西部钻探工程有限公司,新疆克拉玛依 834000)

河流相砂体规模大、物性好,是优质的油气储集体[1],其内部夹层是造成储层层内非均质的重要原因[2],也是控制剩余油分布和采收率的关键地质因素[3]。在其影响下,大庆油田、胜利油田等已进入高—特高含水期的老油田剩余油整体上高度分散,局部相对富集,挖潜难度增大[4]。因此有效地识别夹层是提高采收率的重要环节[5]。目前,夹层研究一方面通过现代沉积和野外露头等建立夹层沉积分布模式[6-7];另一方面通过小井距井间对比,结合注采井动态资料等对夹层厚度、倾角及其展布范围进行定性-定量表征[8]。但密井网区(数千口油水井)夹层识别工作往往面临测井数据资料巨大、识别过程重复、效率低等问题。在大数据和机器学习迅速发展的背景下,寻找一种针对砂体内部夹层及其类别的自动识别方法代替人工识别,具有一定的现实意义。对于研究目标与不确定性特征相关的非线性问题,可以运用机器学习方法建立已知样本集的特征和结果之间的预测模型,对未知样本作尽可能准确的推断。支持向量机(SVM)作为一种常用的机器学习算法,在处理地质问题方面已取得重要进展,已被成功地应用于岩性识别[9]、烃源岩预测[10]、储层流动单元识别[11]和剩余油预测[12]等方面,其识别或预测准确率均超过90%。由此可见,SVM在解决地质问题方面可以达到较高的准确率,具有一定的推广价值。笔者以大庆长垣喇嘛甸油田密井网区辫状河储层为研究对象,对测井数据预处理并提取特征参数作为输入数据集,利用SVM算法进行处理并将夹层类别作为输出,从而达到自动识别的目的,以期提高夹层识别效率。

1 地质概况

喇嘛甸油田位于松辽盆地大庆长垣的最北端,大庆长垣是松辽盆地北部的一个二级构造单元,自北向南发育喇嘛甸、萨尔图、杏树岗、高台子、太平屯、葡萄花和敖包塔7个三级背斜构造(图1),基底主要由古生界加里东、海西期褶皱变质岩系与同期及燕山期花岗岩侵入体组成,上覆沉积的白垩系地层厚度最大,是盆地内主要含油层系[13]。喇嘛甸背斜构造主要形成于燕山运动晚期,也就是上白垩统四方台组—明水组(K2s—K2m)沉积时期[14]。

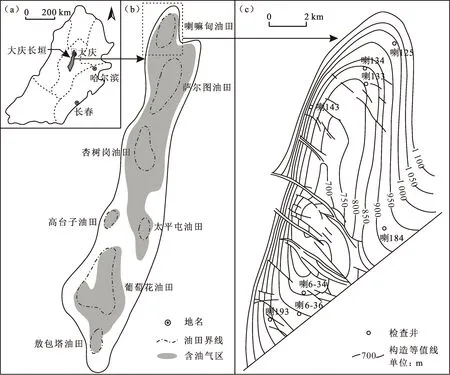
图1 喇嘛甸油田区域地质概况及其构造特征(据文献[19]修改)

研究的目的层段葡萄花油层一段2砂层组(PI2)位于上白垩统姚家组(K2y)。直到青山口组(K2qn)沉积期松辽盆地仍处于坳陷发展阶段,但沉降速度缓慢,湖岸线到达喇嘛甸油田北部,湖盆面积已基本达到最大[14]。进入姚家组(K2y)沉积期,由于湖盆的抬升,湖水变浅,湖盆面积急剧缩小,湖岸线向南收缩到杏树岗地区的南部,使得喇嘛甸地区整体以相对高能的河流沉积为主[14]。

2 SVM原理与数据处理

2.1 SVM算法原理

SVM是由Vapnik提出的一种新型机器学习方法[15],通过核函数将非线性问题的变量映射到高维特征空间,构造最优分类超平面实现线性分类(图2)。对于给定的变量样本集(xi,yi),i=1, 2, …,n,xi∈Rd为输入变量;yi∈{1,-1},为输出变量,那么最优超平面满足:

图2 基于SVM核函数的输入空间到特征空间的数据映射

yi[wTφ(xi)+b]≥1-ξi.

(1)

式中,wT为多维向量;b为常数;ξi≥0为一个松弛变量,控制分类误差。

为最大程度地增加两个类别之间的距离,那么该分类问题可转化为带有惩罚项的最小化问题,式(1)可改写为

(2)

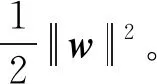
由于目标函数(2)和约束条件(1)构成了一个不等式约束问题,求解此不等式可引入以下拉格朗日函数:

(3)

式中,αi≥0为拉格朗日乘数。

对式(3)w和b求偏导数,以上问题转化为对偶函数的优化问题,借助于核函数K(xi,xj),SVM可以实现对这一非线性可分离样本进行线性分类,约束函数可以表示为

(4)

式中,K(xi,xj)为非线性映射问题中的内积核函数,即K(xi,xj)=φ(xi)·φ(xj)。本文中选择高斯径向基核函数(RBF),它在解决非线性分类问题方面优于其他核函数[16]。假设αi*是该二次函数的最优解,即支持向量,那么以上问题的最优分类函数为

(5)

式中,b*为分类临界值。

2.2 输入特征参数与输出变量

测井特征参数的选取是储集层夹层自动识别的关键,选择与夹层相关性或敏感程度较高的自然电位、自然伽马、微电极、声波时差4条曲线,可以综合反映各不同类型夹层的粒度、泥质含量、孔隙度等特征。为提高训练模型的准确性,需要选取尽可能多的输入特征参数,选用自然电位(最大值、最小值、平均值)、自然伽马(最大值、最小值、平均值)、微电极(微电位、微梯度、微电位和微梯度差)、声波时差(最大值、最小值、平均值)共12种测井特征参数作为输入特征,即夹层特征集X;根据研究区辫状河储层夹层的种类,以Y={Ⅰ,Ⅱ,Ⅲ}作为输出值,其中Ⅰ类代表物性夹层,Ⅱ类代表泥质夹层,Ⅲ类代表钙质夹层。

2.3 参数寻优

参数寻优属于SVM算法样本学习的训练过程,关系着模型识别的准确率。核函数建立后还需优选出最优的高斯径向基核函数半径g和惩罚因子C,从而使SVM模型取得最准确的分类结果。采用目前较为常用的网格搜索和十折交叉验证相结合的方法进行参数寻优,其基本流程如图3所示。通过逐渐缩小网格搜索的范围和步长,寻找使交叉验证精度最优的参数值,最终确定最优的训练参数(g,C)。

图3 参数寻优网格搜索法基本流程

2.4 数据降维

对输入参数进行特征选择,减少数据的维度,尽可能消除数据集中与类别关联较小的特征,可以更好地提升分类精度,其中主成分分析(PCA)可以较好地解决信息冗余问题。故采用PCA对特征参数进行降维处理,其原理主要是通过线性变换把高维空间的数据沿着区分度最小的方向映射到低维空间,从而达到降维的目的。

假设输入样本集X=(x1,x2,…,xm)为n维向量,将其降维到k′得到样本集Y,则首先对样本进行中心化处理,那么中心化后样本之间的协方差和协方差矩阵[17-19]分别为

(6)

(7)

在此基础上求协方差矩阵C的特征值λ和对应的特征向量u,满足

Cu=λu.

(8)

将特征值按照从大到小的顺序排序并选择累积方差贡献率大于85%的前k个λ(λ1,λ2,…,λk),将其相应的特征向量u(u1,u2,…,uk)作为行向量组成特征向量矩阵P,则可得

Y=PX.

(9)

式中,Y即为降维到k维后的样本数据。其中选取最大的前k个特征值和相对应的特征向量,并进行投影的过程,就是降维的过程。

3 不同类型夹层特征

通常,根据沉积和成岩等因素的影响可以把夹层分为3类,即泥质、物性和钙质夹层[20],不同成因的夹层其测井响应特征和厚度差别较大。

3.1 物性夹层

物性夹层通常是由于后期流水作用,冲刷之前河道的泥质沉积物,在相对较弱水动力条件下细粒沉积物的混合沉积。研究区物性夹层的岩性主要为泥质粉砂岩,厚度分布范围为0.15～0.3 m,具有较低的孔渗性能,相对较厚的物性夹层有一定的遮挡能力。物性夹层测井响应常呈现出自然电位曲线轻微回返;自然伽马值小幅升高;微电极曲线略有回返,且有一定幅度差;声波时差曲线表现为中等数值(图4(a),岩心来自L5-J3512和L6-J3555)。

3.2 泥质夹层

泥质夹层一般是由于水动力减弱,在短期的弱水动力环境下细粒悬移沉积物稳定沉降而成。喇嘛甸地区辫状河储层中泥质夹层主要为泥岩或粉砂质泥岩,厚度一般为0.05～0.25 m,通常小于物性夹层厚度。由于孔隙度和渗透率均非常低,泥质夹层对流体表现为完全阻挡,也是最为常见的夹层。其测井响应主要表现为:自然电位曲线靠近泥岩基线,明显回返; 自然伽马值出现大幅升高的现象;微电极曲线呈低值且幅度差很小,几乎为零;声波时差曲线呈现高值或略微增加(图4(b))。

3.3 钙质夹层

钙质夹层主要与河道砂质沉积物的碳酸盐岩胶结作用有关,一般是成岩非均质的表现。研究层位的钙质夹层出现的频率较低,岩性主要为薄层钙质粉—细砂岩,厚度一般为0.05～0.1 m,但其密度大、孔渗性低,对流体流动有一定的遮挡作用。钙质夹层的微电极曲线与前两者具有明显的差别,微电极呈现明显的高值,呈尖峰状;自然电位和自然伽马曲线略有回返;声波时差曲线明显低值(图4(c))。

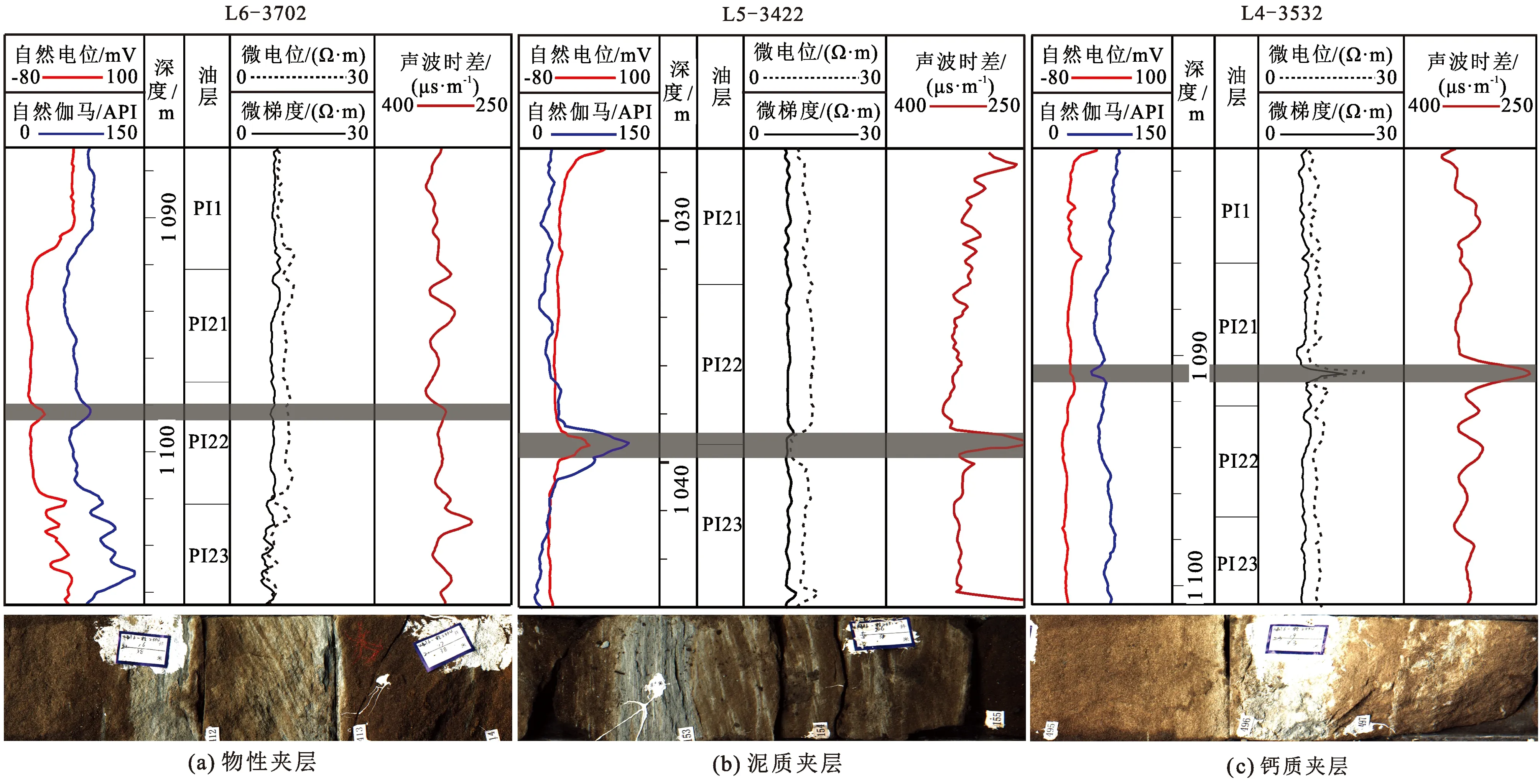
图4 喇嘛甸油田辫状河砂体夹层类型及其测井响应特征

在对研究区的夹层定性识别后,笔者基于94个夹层样本定量统计了3类夹层的自然电位、自然伽马、微电极和声波时差的测井响应结果(表1),可将其作为喇嘛甸油田辫状河储层夹层半定量判别的依据之一。

表1 基于测井资料的辫状河夹层判别标准

4 基于SVM算法的夹层识别

不同类型夹层所对应的测井特征(曲线幅度、形态、光滑程度、幅度差等)具有差异性,因此利用SVM方法,针对测井特征进行储集层夹层识别具有理论上的可行性。

4.1 基于未降维特征参数的夹层识别

首先选择未降维的测井数据作为特征参数,应用高斯径向基函数作为核函数的SVM用于辫状河储层夹层识别。SVM的识别准确率高度依赖于径向基核函数内核的半径g和惩罚因子C[16]。由于没有确定最优参数的特定规则,在此通过反复试验的方法找到g和C的最佳值。

图5(a)为未降维测井参数的SVM分类精度和用于选择最佳参数的网格搜索方法的实验结果。当SVM径向基核函数(RBF)的半径g和惩罚因子C持续变化时,分类精度先从77.5%上升,达到稳定状态为87.5%。实验结果表明,基于未降维测井特征参数识别测试的交叉验证精度达到86.67%,通过网格搜索获得的最优参数g和C分别为0.23和29.86。在对SVM模型训练之后,基于未降维测井特征参数直接识别夹层的结果如图6(a)所示,识别准确率为86.17%。其中实际值来自于测井曲线定性解释,预测值表示SVM定量识别。经过比较SVM的训练和识别表现,可以观察到SVM对于测试数据的识别能力与SVM对于训练数据的识别能力几乎相当,证明了SVM对于未降维测井数据的夹层识别具有一定的泛化能力,但识别精度相对较低。

图5 网格法参数寻优及验证精度

图6 基于SVM算法的辫状河储层夹层识别结果

4.2 基于PCA降维特征参数的夹层识别

由于直接选择未降维的测井数据作为特征参数的SVM识别准确率相对较低。如前所述,测井数据的冗杂会影响到夹层的识别精度,因此尝试对测井数据进行PCA降维处理作为特征参数进行辫状河夹层的SVM识别。

利用Matlab在SVM算法中对样本集的12种特征参进行PCA降维处理后,训练样本集(特征参数)主成分累积方差贡献率如图7所示。显然,经过PCA降维后前6种主成分方差贡献率累积达到86.32%,已经可以代表原始样本集的大部分特征,并且在一定程度上消除了参数冗余,前6种主成分的各个特征参数的系数见表2,表明了各主成分中不同测井特征参数对夹层识别影响的相关性和程度。

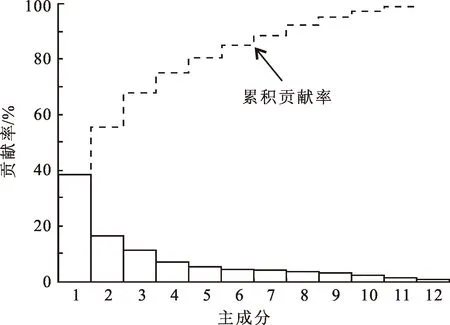
图7 测井特征参数主成分贡献率及累积贡献率

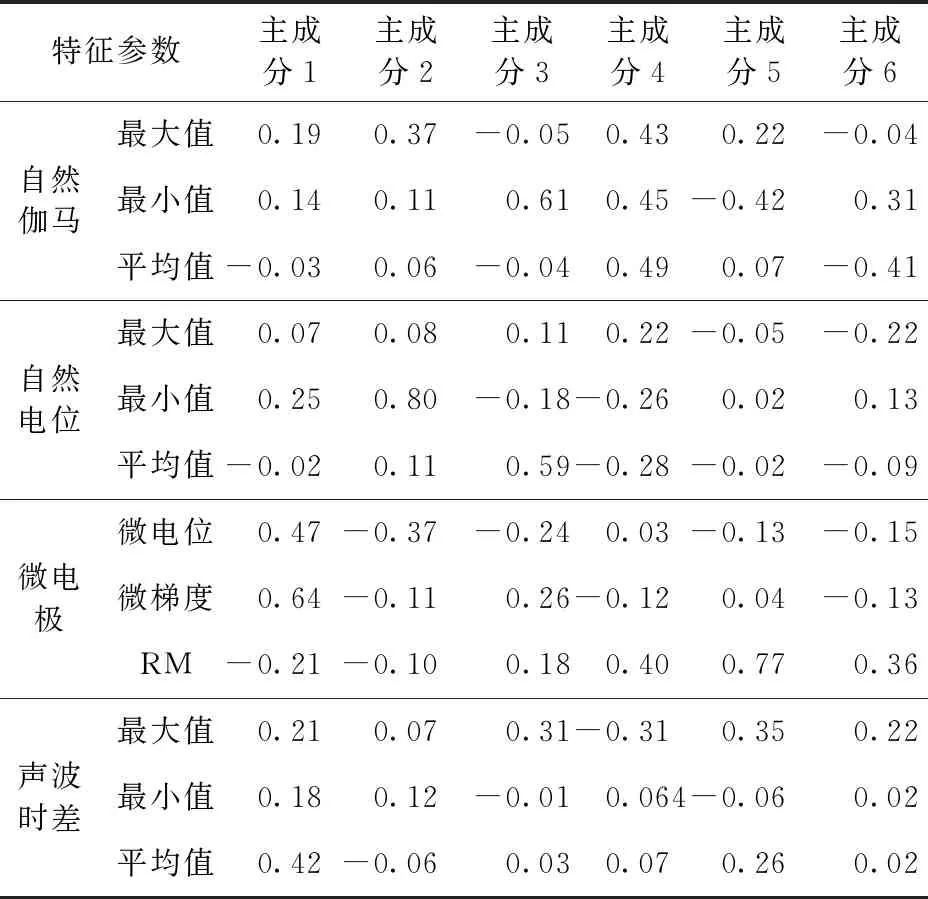
表2 前6种测井特征参数主成分相关系数

对于降维后的测井特征参数,最优高斯径向基核函数半径g和惩罚因子C仍采用网格搜索反复试验获得。图5(b)显示了降维后的SVM分类精度和用于选择最佳参数的网格搜索方法的结果。随着高斯径向基核函数半径g和惩罚因子C的变化,训练样本集的SVM交叉验证精度最高可以达到93.33%,此时的最优参数g和C分别为0.29和34.30。在以上SVM模型训练之后,基于降维的测井特征参数识别沉积夹层的结果如图6(b)所示,识别准确率为92.55%。对比降维前后SVM的识别发现,特征参数降维后的SVM识别准确率提高了6.38%,这表明SVM对于降维测井数据的辫状河夹层识别具更强的泛化能力。

4.3 SVM模型应用性能分析

本文中主要讨论对辫状河储层夹层识别准确率更高的PCA降维后的SVM模型的性能(图6(b))。基于4类测井数据的12个特征参数,经PCA降维处理作为SVM的输入参数,识别结果表明当核函数半径g为0.29,惩罚因子C为34.30时,SVM的识别性能最优。具体而言,94个测试样本中出现87个正判,7个误判,其中5个“Ⅰ”类错判为“Ⅱ”类,2个“Ⅱ”类样本错判为“Ⅰ”类,Ⅲ类样本未出现误判。以取芯井L6-J3555为例,基于PCA的SVM模型对辫状河砂体夹层的识别结果与人工定性识别整体上具有较高的吻合度,仅出现一个物性夹层误判为泥质夹层(图8)。

图8 密闭取芯井L6-J3555辫状河储层夹层PCA-SVM识别结果

通过对错判样本的分析发现,SVM对不同类型夹层的识别准确率存在差异,尽管钙质夹层训练样本数量少,但由于其微电极曲线显著的差异性特征导致识别准确率最高。样本较多的泥质和物性夹层二者在测井表现上存在一定的相似性,少量夹层测井响应差异不明显,因此误判的样本多出现在这两类夹层之间(图6)。此外,由于测井资料的限制,选取的测井参数也很难完全地体现泥质和物性夹层的全部特征,存在着系统误差。但是,92.55%的准确率对于密井网区辫状河夹层的识别基本可以满足地质上的需求。如果用地质规则来监督算法,那么SVM对地质问题识别的准确性会进一步提高[16]。

SVM算法在实践中的表现往往优于其他机器学习算法的原因是,它们对训练集中的异常值不太敏感,因此不太容易过度拟合。此外,SVM的性能受训练数据集大小的影响较小,这是它作为机器学习方法的一个优点。在大数据迅速发展的今天,SVM在解决地质大数据的特定问题上具有一定的可行性,可以有效地减少重复而繁杂的工作量,提高工作效率。