高速铁路大跨度中承式钢桁拱桥设计研究

2021-08-08闫岩

铁道建筑 2021年7期

闫岩

中铁第一勘察设计院集团有限公司，西安710043

我国现代钢拱桥技术起步较晚，发展较慢。基于我国独特的地理环境条件和国外技术经验，我国建成了多座世界先进的钢拱桥（表1）。如建成的大瑞（大理—瑞丽）铁路怒江特大桥，主拱跨度为490 m，采用上承式钢桁拱桥形式，一跨过江，刷新了我国铁路钢拱桥的记录，标志着我国钢拱桥设计理论和施工工艺的修建技术处于国际领先水平［1-3］。

表1 国内已建成部分铁路钢拱桥

现代钢拱桥多采用高强材料，承载能力已不是起控制作用的因素。提篮拱桥由于改变了传统拱结构的静力计算图式而获得较大的横向稳定性，解决了拱桥施工中的横向面外稳定性问题［4］，但是中承式钢桁拱桥在我国铁路桥梁领域尚无应用实例。本文以西十高速铁路铁路汉江特大桥为对象，对中承式钢桁拱桥的结构设计及重点结构参数进行研究。

1 工程概况

西十高速铁路是设计时速350 km的双线高速铁路，位于陕西省东南部和湖北省西北部，汉江特大桥是西十高速铁路的控制性重难点工程。桥址处呈现开阔的深U形河谷，河谷宽度约500 m，设计轨面与最高水位高差约30 m。桥址两岸基岩裸露，桥址处断裂构造不发育，工程地质条件较好。对于跨度400 m左右的桥梁，可采用拱桥、斜拉桥和悬索桥。结合桥址条件，低桥位方案宜采用中承式钢桁拱桥方案［5］。该方案不仅能够满足通航要求，避免深水基础，且对自然环境的影响较小。中承式钢桁拱桥桥梁结构刚度大，受力性能优，景观效果好。

2 中承式钢桁拱桥结构设计

主桥为1×420 m中承式提篮钢桁拱结构，采用2片拱形桁架，通过平联及横联连接成整体。跨径布置为（31.5+31.5+360+35+35）m，两侧均接桥台，主桥全长为509.9 m。全桥上弦矢跨比1∕4.15，下弦矢跨比1∕3.86，拱轴线均采用二次抛物线，主桁为N形桁架，拱顶和拱脚处拱肋面内桁高分别为8、15 m，2片桁架内倾3.5°。拱脚处2片桁架间距25 m，节间水平投影长度10 m。

2.1 拱肋

弦杆为箱形截面，上弦截面尺寸1 600 mm（高）×1 600 mm（宽），下弦截面尺寸1 600～2 000 mm（高）×1 600 mm（宽），板厚32～50 mm，主桁采用焊接整体节点结构形式。为满足局部稳定的要求，在箱形截面四面每块板上设置一道纵向加劲肋。箱形截面杆件内设置横隔板，板厚16 mm，横隔板间距不大于3 m。主桁腹杆除横梁处为箱形截面，其余均为H形截面，H形截面高1 600 mm，翼缘截面宽1 000～1 600 mm，板厚24～40 mm。为满足局部稳定的要求，H形截面腹板设置2道纵向加劲肋。主桁杆件均采用Q370qD钢材。

拱肋上、下弦平面内设平联，米字形布置；部分平联采用1 000 mm×800 mm的工字形截面，板厚24 mm，部分平联采用1 200 mm×1 200 mm的箱形截面，箱形截面四面每块板设置一道纵向加劲肋。主梁以下拱肋每个节间均设置横联，主梁以上拱肋每2个节间设置1处横联，全桥共21处。横联杆件采用1 000 mm×800 mm的工字形截面，板厚24 mm。横向联结系采用Q345qD钢材。拱肋立面布置见图1。

2.2 主梁

综合考虑铁路限界、接触网柱、电力、通信信号电缆槽等控制因素，桥面结构宽取17.0 m（图2），吊杆横向间距14.4 m。主梁采用正交异性钢箱梁，顶板厚16 mm，底板厚18 mm，腹板厚24 mm。顶底板均采用U肋加劲，顶板U肋厚10 mm，间距600 mm；底板U肋厚8 mm，间距800 mm，腹板采用板肋加劲，沿桥梁纵向每隔3 m设置横隔板。主梁采用Q370qD钢材。

2.3 吊杆

短吊杆采用PES7-223型和PES7-151型平行钢丝束成品吊杆，其余吊杆采用PES7-127型平行钢丝束成品吊杆，锚具采用对应规格的锚固装置。全桥共设31对柔性吊杆，吊杆最长为67.4 m。吊杆上端锚固于拱肋下弦杆，下端锚固于钢箱梁锚固区域。

2.4 拱座

主拱基础采用分离式斜桩+竖直桩嵌固基础，全桥共设4个拱座。拱座采用C40混凝土，拱座宽10 m，高18.6 m，拱肋深入拱座6 m（图3）。拱脚处拱肋下弦内填充混凝土，通过在拱肋的端部焊接端板和加劲肋的方式增强局部承压能力。基础竖直桩采用8 m×8 m方桩，斜桩采用7.0 m×8.5 m的马蹄形断面。

图3 拱脚立面（单位：cm）

2.5 计算模型及荷载

采用MIDAS∕Civil软件建立有限元模型，拱肋杆件和主梁均采用梁单元模拟，吊杆采用桁架单元模拟。全桥模型共有1 128个单元，561个节点。

钢结构自重考虑整体节点板等构造，对其重度进行调整计算；二期恒载为180 kN∕m；考虑基础变位的影响进行最不利工况组合；列车活载采用ZK活载图式；列车横向摇摆力为l00 kN，将其作为一个集中活载作用于桥梁结构最不利位置，作用点位于垂直线路中心线的钢轨顶面；瞬时最大风速为17.8 m∕s，基本风压取400 Pa；全桥整体升温30℃，降温25℃；钢拱桥上下游侧面温差为±10℃。

2.5.1 主梁静力计算结果

计算主桥主要杆件在主力、主力+附加力作用下的受力，结果见表2。可知，拱肋上下弦均受压，上弦拱顶和下弦拱脚钢混结合处为受力最不利位置。

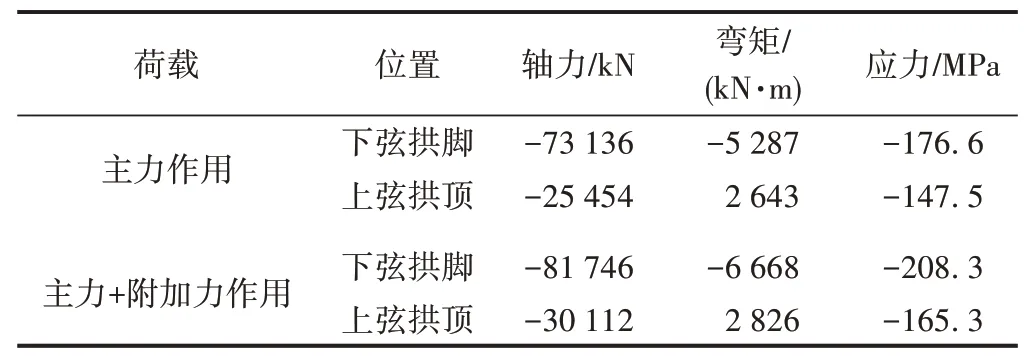
表2 主桥主要杆件计算结果

2.5.2 主梁刚度

利用有限元软件移动荷载分析模块对全桥进行影响线分析，计算得到主桥刚度指标，见表3。

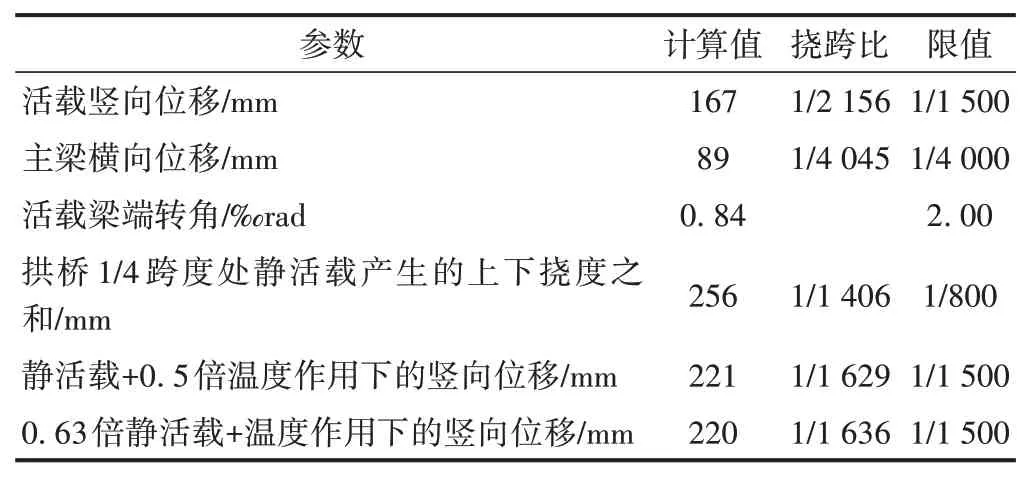
表3 主桥刚度指标

由表3可知，结构最小竖向挠跨比为1∕1 629，横向挠跨比为1∕4 045，均满足TB 10002—2017《铁路桥涵设计规范》要求。桥梁整体刚度较大，能很好地满足行车安全及舒适性的要求。

2.5.3 运营整体稳定系数

对钢桁桥进行稳定分析得到成桥阶段（恒载作用）和运营阶段（中跨布置双线活载）的稳定系数，见表4。可知，该在成桥阶段及运营阶段稳定系数最小值为12.74，大于TB 10002—2017中规定的4.00，表明该桥稳定安全系数较大，整体具有较好的稳定性。

表4 整体稳定系数

2.5.4 车桥耦合动力仿真结果

CRH3动车组以速度180～420 km∕h通过中承式钢桁拱桥时，动车与拖车的脱轨系数、轮重减载率、轮轨横向力等安全性指标均在限值以内，保证了高速列车的行车安全，竖向和横向舒适性均达到优，其动力性能符合要求。

3 技术难点及关键点

3.1 拱圈拱轴线的选取

拱桥拱轴线的线形对结构弯矩分布影响较大，合理的拱轴线形使得拱肋各部分杆件受力均匀，更方便统一杆件截面尺寸［6-7］。该桥采用悬链线拱轴线，选取拱轴系数m为1.0、1.3、1.6和2.0进行对比分析。拱轴系数为1.0时拱轴线为二次抛物线。

3.1.1 拱轴线对轴力的影响

主力作用下不同拱轴系数的拱肋轴力对比见图4。可知：拱轴系数从1.0增至2.0，上弦拱脚轴力增加了42%，上弦拱顶轴力增加了21%，下弦1∕4处轴力增加了16%，而下弦拱脚轴力减小了17%，下弦拱顶轴力减小了26%，上弦1∕4处轴力减小了19%。

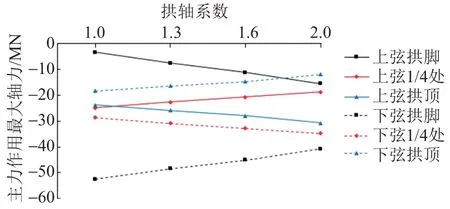
图4 主力作用下不同拱轴系数的拱肋轴力对比

3.1.2 拱轴线对弯矩的影响

主力作用下不同拱轴系数的拱肋弯矩对比见图5。可知：拱轴系数为1.3时，下弦拱脚负弯矩变为正弯矩，其变化最剧烈；上下弦拱顶的正弯矩随拱轴系数的增大而增大，但变化幅度较小；上下弦1∕4处的正弯矩随拱轴系数的增大而减小，但变化幅度不大。

图5 主力作用下不同拱轴系数的拱肋弯矩对比

3.1.3 拱轴线对偏心距的影响

不同拱轴系数的偏心距见图6。可知：①上弦拱脚偏心距随拱轴系数变化最剧烈。当拱轴系数为1.0时，主力最大作用下拱脚偏心距为-45.2 mm，主力最小作用下拱脚偏心距为134.9 mm；当拱轴系数为2.0时，主力最大作用下拱脚偏心距为-261.8 mm，主力最小作用下拱脚偏心距为33.49 mm。②下弦拱顶和拱脚偏心距幅值随拱轴系数增大而增大。当拱轴系数为1.0时，主力最大作用下拱脚偏心距为38.4 mm，主力最小作用下拱脚偏心距为129.66 mm；当拱轴系数为2.0时，主力最大作用下拱脚偏心距为-104.1 mm，主力最小作用下拱脚偏心距为50 mm。

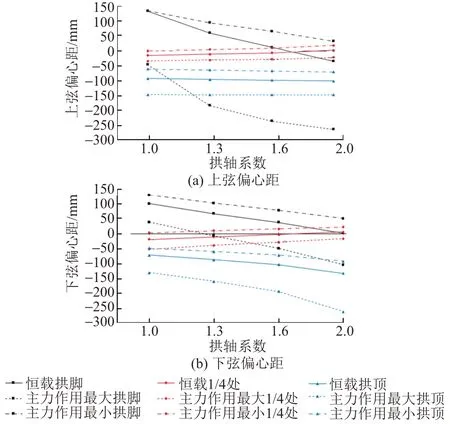
图6 不同拱轴系数的偏心距

综上，当拱轴系数为1.0时，在主力作用下，上下弦偏心距相对值接近0，更靠近合理拱轴线。为保证拱肋杆件在全拱轴线上受力均匀，使杆件截面尺寸变化合理，该桥拱轴系数取1.0，采用二次抛物线作为弦杆拱轴线。

3.2 内倾角

拱桥结构支承的荷载达到临界值时，整个拱结构失去平衡稳定性，或在拱的平面内发生纯弯屈曲，或倾出平面之外发生弯扭屈曲。因此，有必要研究大跨度拱桥的稳定性。

拱肋横桥向倾斜一定角度可显著提高拱桥的稳定性，增大主拱的稳定安全系数，特别是对宽跨比较小的窄桥，拱肋内倾对其横向稳定性的影响非常显著［8］。但是对于钢桁拱桥，其单侧拱肋抗扭刚度及横向刚度很小，横向稳定性由横撑（平联）提供，一旦内倾，其稳定性会降低。

根据桥面布置及限界，固定拱梁交汇处的横梁长度为20 m，以此为基点旋转拱肋，分别对内倾1°～5°进行计算。不同内倾角时拱肋间距见表5，整体稳定安全系数对比见图7。

表5 不同内倾角时拱肋间距

图7 不同内倾角整体稳定安全系数对比

由图7可知：①拱肋横向整体稳定系数随内倾角的增大而降低，且下降速率增加。当内倾角为5°时，成桥阶段横向整体稳定安全系数为16.17，满足TB 10002—2017要求的整体稳定安全系数大于4.00的要求。②拱肋竖向稳定系数随内倾角的增大而增加，但是增加幅度不大，说明拱肋内倾能够小幅提高钢桁拱桥的竖向稳定性。

从平联设置方面考虑，由于节间距取10 m，当内倾5°时，拱顶间距为6.2 m，平联与弦杆的夹角为31°（图8），节点板设置十分困难，且小角度杆件次内力会增加。提篮式拱桥的拱肋内倾后会降低拱肋横向稳定性，但仍在安全范围内，故该桥内倾角采用3.5°。

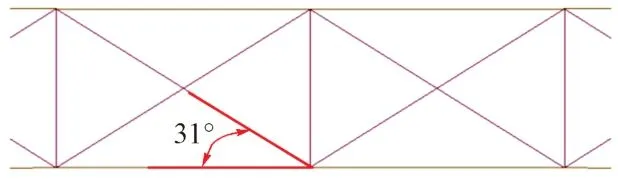
图8 内倾角5°时拱顶构造

3.3 拱脚下弦杆结构优化

拱轴线为二次抛物线，拱肋上下弦基本受力均匀，但是下弦拱脚受力较大，拱肋下弦须采用1.6～2 m（高）×1.6 m（宽）的箱形截面，拱脚采用3 m（高）×2 m（宽）的截面才能满足受力要求。为保证拱桥下弦截面高度一致，在下弦拱脚的箱形截面内灌注C50自密实补偿收缩混凝土，从而提高拱脚的受力性能［9-10］。当拱脚不灌注混凝土时，拱脚下弦杆主力作用下的应力为190.7 MPa，而灌注混凝土后应力为161.5 MPa。灌注混凝土对钢桁拱桥横向刚度有一定提高，且箱形尺寸能与其他下弦杆件保持一致，故推荐在拱脚下弦杆内灌注混凝土的方案。

3.4 主梁形式比选

拱桥多采用由混凝土桥面板与钢主梁和钢横梁形成的结合梁体系。基于减振、降噪、结构受力和耐久性的需要，选择4种主梁方案（表6）进行比选：方案1，混凝土桥面板结合梁；方案2，正交异性板钢纵横梁；方案3，正交异性板钢箱梁；方案4，混凝土桥面板扁平钢箱。不同主梁方案工程量和造价对比见表7。

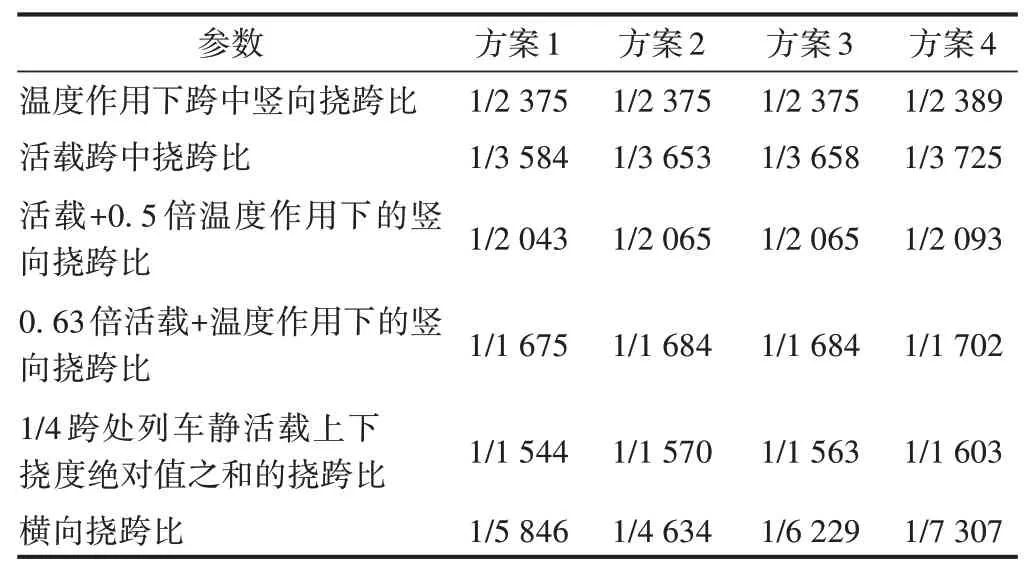
表6 不同主梁方案挠跨比

表7 不同主梁方案工程量和造价对比

由表6和表7可知：4种方案的竖向刚度非常接近，横向刚度差别大；方案2横向刚度最差，在风荷载和摇摆力及温度作用下的横向挠跨比达到了1∕4 634，接近限值1∕4 000。综合工程量估算和整体计算结果，方案1和方案3的刚度较好，虽然方案3用钢量较大，但方案1的工程造价略高于方案3，即便进一步优化结合梁的构造，其工程造价优势并不明显。因此设计时优选方案3。