基于自适应RBF神经网络的连续压力波信号滤波方法
2021-08-08宋晓健薛文伯马鸿彦陈维海
宋晓健,刘 勇,薛文伯,马鸿彦,陈维海,陈 菲
(1.中国石油集团渤海钻探工程有限公司 定向井技术服务分公司,河北 任丘 062552;2.中国石油测井公司 华北分公司,河北 任丘 062500; 3.中国石油集团测井有限公司 长庆分公司,陕西 西安 710065)
引 言
钻井液连续压力波信号频率一般在15~30 Hz,上传过程中会受到钻井泵、井下振动、钻井液性能、传输距离的影响,与高频噪声信号在频域上存在混叠现象,有用钻井液连续压力波信号往往湮没在噪声中,固定参数滤波器难以满足滤波需求。
Jarrot A等[1]提出了钻井液泵噪声消除法, 通过模拟泵噪声频谱特征,消除实际压力脉冲中的噪声。李红延等[2]提出了一种基于小波包变换的钻井液压力信号滤波算法, 上述滤波算法的研究克服了傅里叶变化仅在频域中进行的问题,取得了一定效果,但是该方法受小波基选择和分解层数的影响很大,滤波效果不稳定。杨金显[3]提出了小波变换与经验模态分解相结合的滤波方法,该算法虽然可以在一定程度上抑制模态混叠现象,但每个重构分量难以确定,且其计算量较大。沈跃[4]提出了针对钻井液压力信号的自适应滤波算法,无需对噪声信号进行系统建模, 但自适应滤波器算法的学习步以确定。
针对上述滤波问题,通过分析钻井液连续压力波信号的频域特性,本文提出了一种小波包变换结合自适应变步长RBF(Radial Basis Function,RBF)神经网络非线性滤波器的滤波方法。
1 钻井液连续压力波信号的频域特性分析
某公司连续波仪器的钻井液连续压力波信号调制原理是通过可变幅度脉冲序列在信号零点处进行相位调制。压力传感器采集到的钻井液连续压力波信号频谱如图1所示,包含有用钻井液连续压力波信号、低频噪声和高频噪声信号,有用信号的中心频率在12~15 Hz,低频噪声在0~10 Hz,高频噪声在10~50 Hz,噪声信号强度大分布广且没有规律。有用钻井液连续压力波信号和高频噪声信号在频域上出现大量重叠,且有用钻井液连续压力波信号具有突变型、非线性等特点,采用固定参数的滤波算法,滤波信号出现相位延迟、频谱缺失等问题,严重影响信号检测。
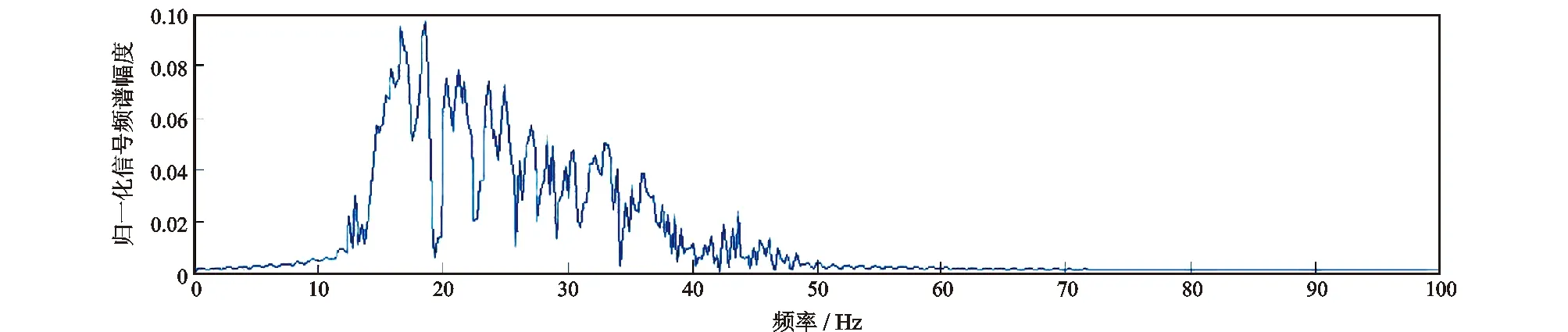
图1 钻井液连续压力波信号频谱分析Fig.1 Spectrum analysis of continuous pressure wave signal of drilling fluid
2 RBF神经网络非线性滤波器分析
2.1 钻井液连续压力波信号滤波流程
基于小波包变换与自适应变步长RBF神经网络非线性滤波器的滤波方法流程图如图2所示。
该方法步骤为:①对发码的钻井液连续压力波信号采用小波包分解,根据分层阈值滤波算法和奇异值分解算法,获得含噪声的有用连续压力波信号,同时对不发码的钻井液连续压力波信号进行带通滤波,获得噪声相关信号;②将上述两路信号延时后,同步输入RBF神经网络非线性滤波器中,根据自适应变步长滤波算法对神经网络参数进行迭代更新,输出误差信号;③误差信号通过FIR低通滤波器,恢复有用的钻井液连续压力波信号。
2.2 自适应变步长RBF神经网络非线性滤波器分析
为了保证滤波后信号不失真,结合钻井液连续压力波信号频域分析,采用RBF神经网络来逼近噪声信号。对于连续非线性函数RBF神经网络具有最佳的逼近性能,相比其他神经网络参数少、收敛速度快、泛化能力强。自适应变步长滤波器能够根据误差大小调整步长,兼顾滤波器的收敛速度和滤波效果[5]。
2.2.1 RBF神经网络非线性滤波器结构和功能
RBF神经网络非线性滤波器的运行分为两步[6-7]:①非线性滤波。利用m个延时采样值和g个隐含神经元高斯基函数激活输入信号并输出响应信号,将该响应信号与期望输入信号进行数值对比,得出误差函数信号。②自适应调整。根据上一时刻获得的误差函数信号,运用自适应变步长滤波算法,调整RBF神经网络参数,实现滤波功能。
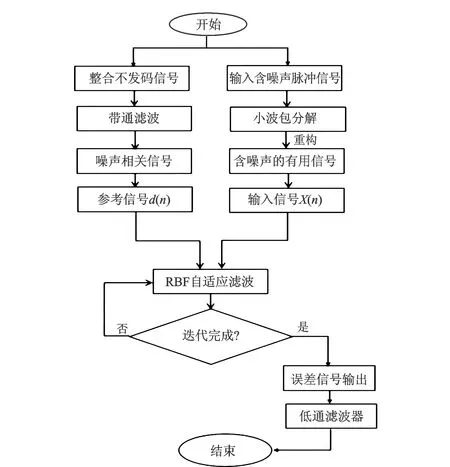
图2 基于小波包变换结合自适应变步长RBF神经网络非线性滤波器滤波方法流程Fig.2 Flow chart of nonlinear filter filtering method based on wavelet packet transform and adaptive variable step RBF neural network
用于非线性滤波的RBF神经网络如图3所示,输入信号通过延时器形成输入信号向量X(n),传递到RBF神经网络中由激活函数sigmoid输出y(n)。
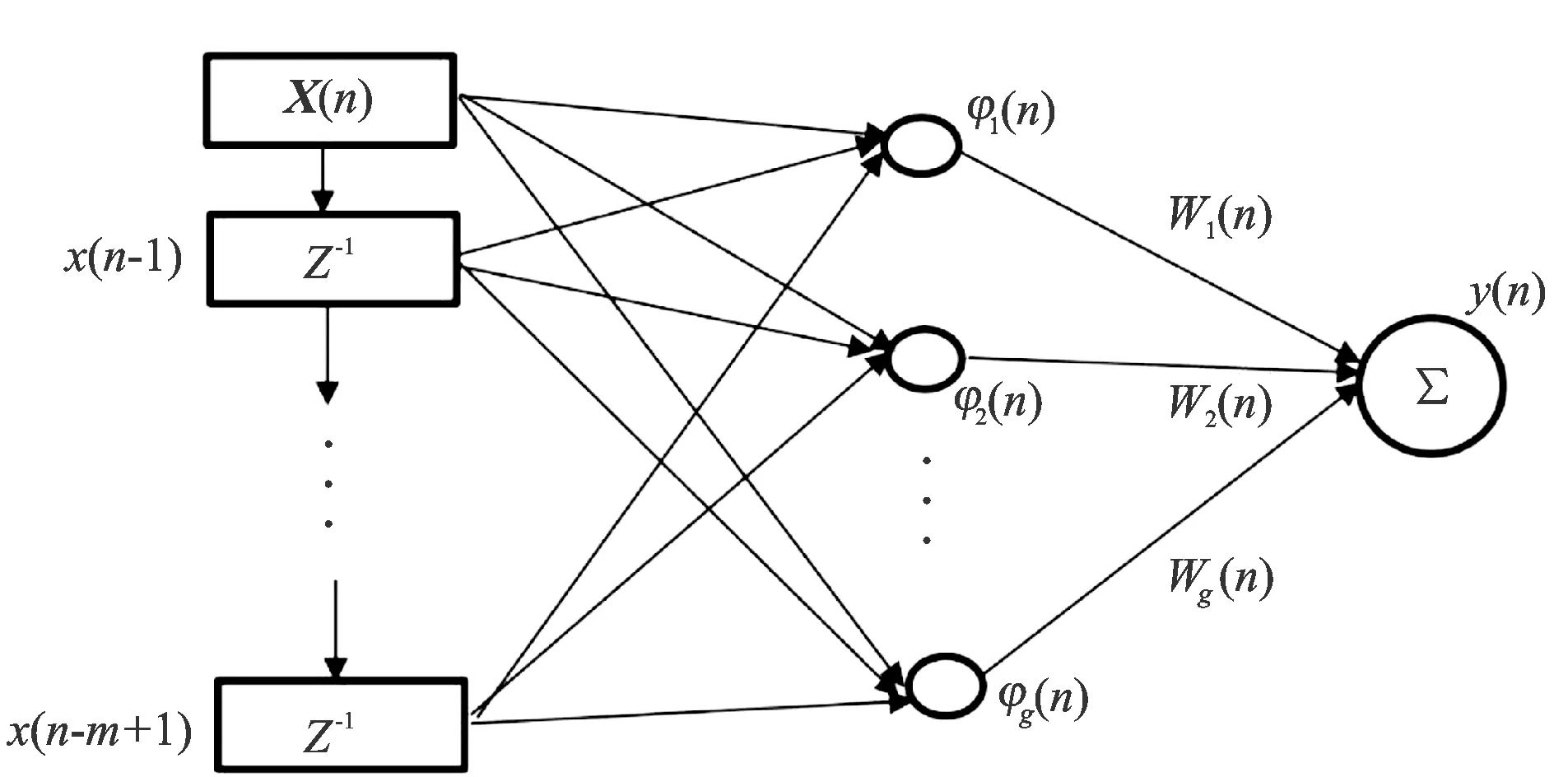
图3 自适应RBF神经网络基本拓扑结构Fig.3 Basic topology of adaptive RBF neural network
输入层中,输入向量
X(n)=[x(n),x(n-1),x(n-2),…,x(n-m+1)]T。
(1)
式中:x(n)为第n时刻受宽带噪声干扰的信号采样值;m为输入信号长度;x(n-m+1)为x(n)信号延时m个单位后的采样值。
隐含层中,φi(n)(i=1,2,…,g)为n时刻第i个隐含神经元对于输入X(n)的响应函数,该函数为高斯基函数,定义为
i=(1,2,3,…,g)。
(2)
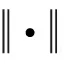
Ci(n)=[ci1(n),ci2(n),ci3(n),…,cim(n)]T,
i=(1,2,3,…,g)。
(3)
输出层中,第n时刻含g个隐藏层神经元的RBF神经网络的输出为
(4)
式中:W(n)为RBF神经网络线性连接权值向量;φ(n)为响应向量。分别定义为
W(n)=[w1(n),w2(n),w3(n),…,wg(n)]T。
(5)
φ(n)=[φ1(n),φ2(n),φ3(n),…,φg(n)]T。
(6)
其中,wi(n)(i=1,2,…,g)为n时刻第i个隐含神经元与输出的线性连接权值。
旅游纪念品本应是某地特有的或特别著名的产品,富有当地的文化历史内涵,有些纪念品甚至只能在当地才能生产。然而,当成百上千个景区都在贩卖长了“同一张脸”的旅游纪念品时,谁还会认为值得购买、值得为“到此一游”留念?据说有人在四川旅游,竟买到了写有“少林寺纪念”的“特产”,如此忽悠手法实在是太低级了。
RBF神经网络非线性滤波器原理如图4所示。
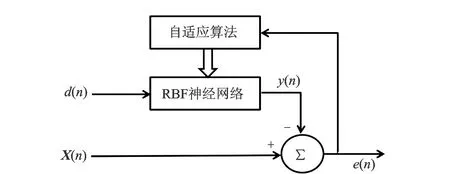
图4 基于自适应变步长RBF神经网络非线性滤波器原理Fig.4 Principle diagram of nonlinear filter based on adaptive variable step RBF neural network
X(n)作为原始输入信号,为经过小波包变换重构后的有用钻井液连续压力波信号的延时信号,可以表示为s(n)+dnoise(n);d(n)作为参考输入信号,为经过带通滤波的噪声相关信号的延时信号;s(n)作为信号源发出的连续压力波信号;dnoise(n)作为噪声信号;y(n)作为RBF神经网络输出信号。e(n)为RBF神经网络输出信号和参考输入信号的误差,则
e(n)=X(n)-y(n)。
(7)
X(n)为连续压力波信号中发码的延时信号序列,存在泵噪声、其他噪声和有用的钻井液连续压力波信号成分。d(n)为连续压力波信号中不发码的延时信号序列,存在泵噪声和其他噪声成分,不存在有用钻井液连续压力波信号[8-9]。由于d(n)与X(n)相关性很低,有用钻井液连续压力波信号在输出信号e(n)中得以最大程度的保存,提升了滤波器的收敛性。
通过对输出e(n)的控制,在线调整RBF神经网络参数,使得RBF神经网络的输出y(n)与d(n)的均方误差最小,则当RBF神经网络稳定后,该非线性滤波器的输出e(n)就是消除了dnoise(n)的期望输出信号s(n)。
2.2.2 自适应变步长滤波算法
钻井液连续压力波信号具有频率变化复杂、与噪声有大量重叠频带的特性,为了加快收敛速度,更好地分离有用钻井液连续压力波信号和噪声,本文提出了自适应变步长滤波算法。该算法通过误差的大小自动调节滤波器的学习步长,滤波初期采用较大的步长获得较快的收敛速度,稳态期间采用较小的步长保持稳态,避免稳态误差失调。
(8)
在n时刻,学习步长对应μ0=[μc0、μσ0、μw0],对应的训练误差代价函数为E(μ0),将代价函数作为学习率的函数。由于可以认为学习步长前后代价函数的取值相差较小,将E(μ)在μ0处三阶泰勒展开得
(9)
令μc-μ0=△,△为学习步长优化量,则
(10)
式(10)中,学习步长优化量与误差代价函数为二次项关系,根据梯度下降法算法,求得误差代价函数E取最小值时的学习步长优化量,更新速度设为0.05△到0.50△。学习步长更新速度取决于上一次迭代结果,如果误差的绝对值降低,则以5%的幅度增大学习步长;如果误差的绝对值增加,返回上一次迭代参数并重置代价函数,将学习步长调整为之前的1/2,继续进行更迭,寻找全局最优解。
3模拟井下接收信号QPSK仿真实验
模拟泵噪声信号为
x(t)=0.5sin(sin4πt)+0.5sin(sin20πt+π/3)+0.5sin(sin44πt+2π/3)。
(11)
模拟信号由QPSK信号[10-14],信噪比4 dB的高斯白噪声信号,2、10、22 Hz周期性模拟泵噪声组成,混合信号波形如图5所示。
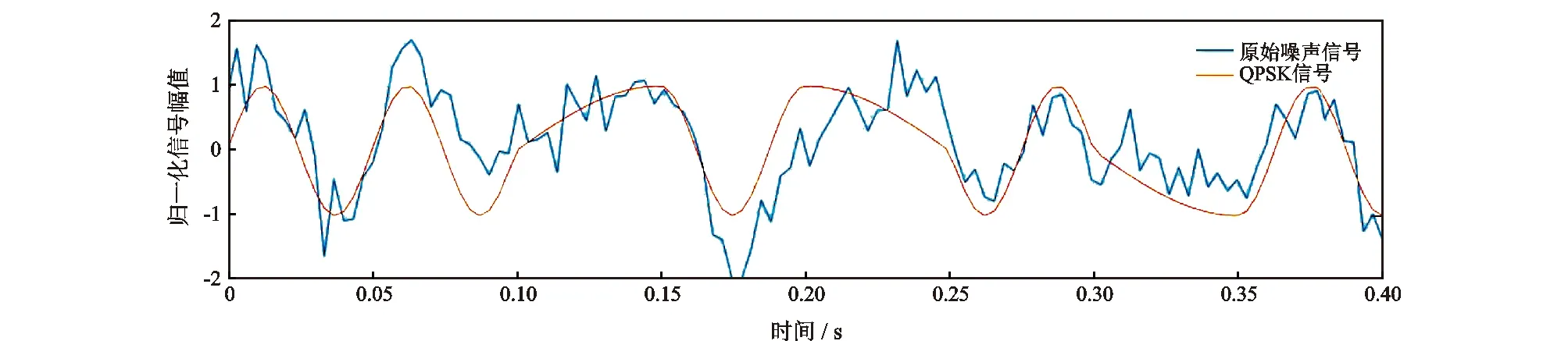
图5 带噪声的模拟信号波形Fig.5 Analog signal waveform with noise
3.1 滤波过程
精确选取RBF神经网络非线性滤波器的原始输入信号和参考输入信号[15-17],步骤为:①通过大量实验,综合考虑滤波后的信噪比、均方误差、相关系数,选择最优小波基;②运用分层阈值滤波算法和奇异值分解算法,获取有用钻井液连续压力波信号;③对多段不发码的信号进行整合,采用带通滤波获得噪声相关信号。
为了提高小波包重构信号的分辨率,对模拟QPSK信号进行小波包分解,选取滤波后的信噪比、均方误差、相关系数作为分解效果衡量参数对小波基进行选择。根据表1和图6对比结果,Db6小波基重构信号的相关系数、信噪比(SNR)为最高,均方根误差(RMSE)最小,所以选取Db6小波基。
模拟信号选用Db6小波基,根据分层阈值滤波算法和奇异值分解算法,对发码信号序列进行小波包变换,得到原始输入信号时序波形如图7所示。
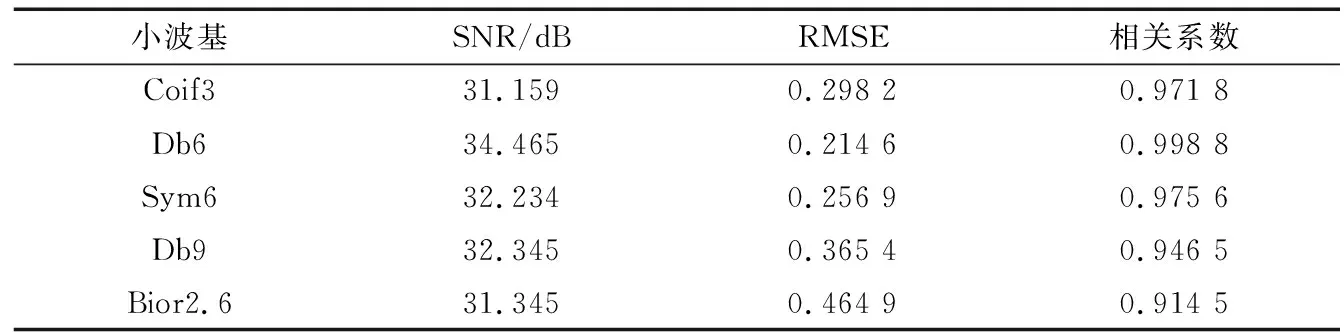
表1 小波基性能比较Tab.1 Performance comparison of wavelet bases
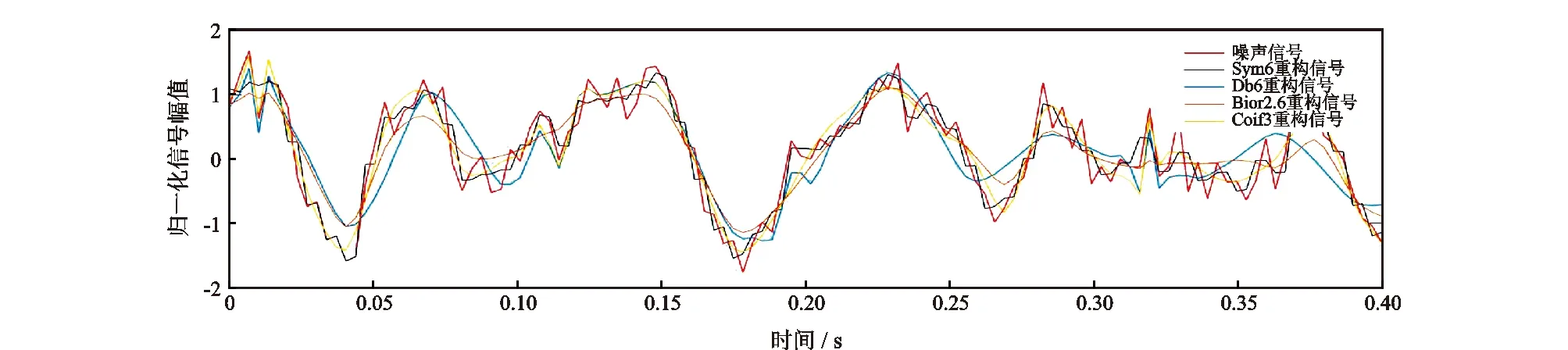
图6 不同小波基重构信号对比Fig.6 Comparison of reconstructed signals with different wavelet bases
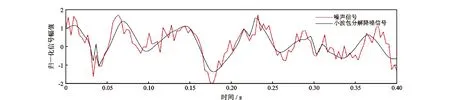
图7 有用连续波压力信号重构信号Fig.7 Reconstructed signal of useful continuous pressure wave signal
由于不发码信号序列主要由周期性的泥浆泵噪声和其他非周期噪声组成,所以选取多段不发码信号序列进行整合,得到与发码信号序列具有相同个数的参考输入信号,如图8所示。对多段不发码信号序列进行带通滤波处理,滤除明显位于钻井液连续压力波信号以外的随机高频、低频噪声和泵噪声。
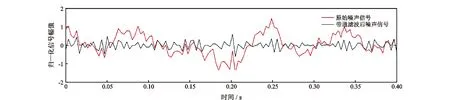
图8 带通滤波后QPSK噪声波形Fig.8 QPSK noise waveform after bandpass filtering
将上述两路延时信号同步输入RBF神经网络非线性滤波器中进行自适应滤波,原始信号波形与滤波输出波形对比如图9所示。滤波后的波形在信号零点处的位置明显,泵噪声信号和随机噪声信号基本被滤除。
3.2 不同滤波算法效果的比较和分析
不同滤波算法频谱对比如图10所示,自适应滤波、小波分解和改进的自适应互补集合经验模式分解(CEEMD)的滤波效果大致相同[18-19],中心频率12~15 Hz 中有用的钻井液连续压力波信号频谱少部分被滤除,约22 Hz的噪声信号没有被滤除。采用新方法滤波后,频率为2 、10、22 Hz的钻井泵噪声基本被滤除,中心频率12~15 Hz的有用连续波信号得到保存。不同滤波算法波形对比如图11所示。新算法滤波后的波形在过零点处无明显噪声,相位检测容易;其他滤波方法在过零点处均有明显噪声,相位检测困难。相同仿真信号的信噪比对比结果见表2,新方法去噪后的信噪比、均方误差、相关系数均高于其他滤波方法。不同仿真信号的信噪比对比结果见表3,随着信噪比的下降,其他算法在信噪比1.023 6 dB时,去噪信噪比受到了很大程度的干扰,但新方法的去噪信噪比均高于其他滤波方法,特别在低信噪比-14.547 0 dB的情况下,新方法去噪信噪比明显高于其他滤波方法。
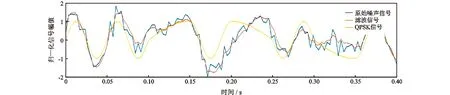
图9 滤波前后的波形Fig.9 Waveforms before and after filtering
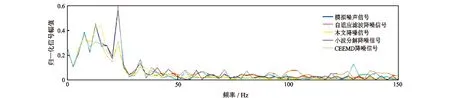
图10 不同滤波算法滤波前后的频谱对比Fig.10 Comparison of spectra before and after filtering using different filtering algorithms
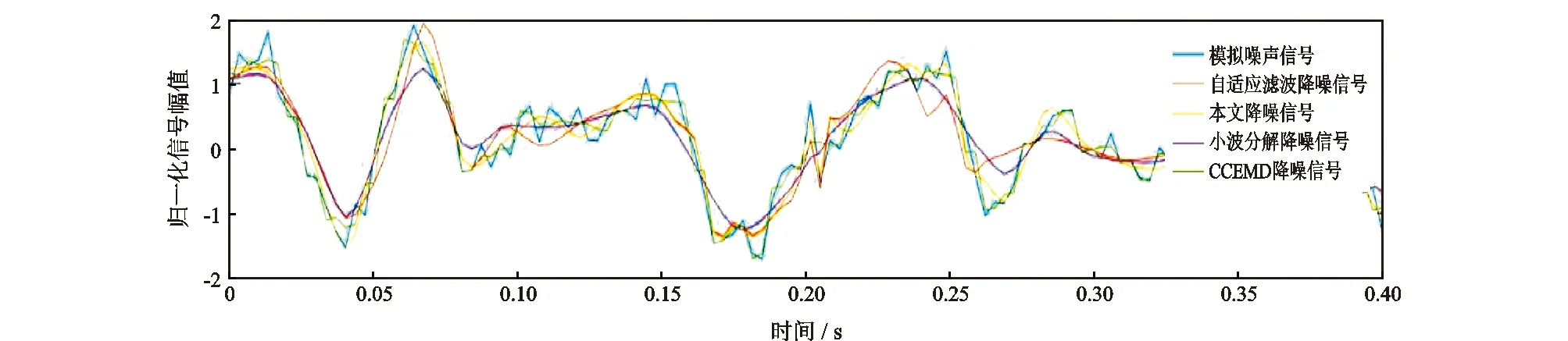
图11 不同滤波器滤波前后波形对比Fig.11 Comparison of waveforms before and after filtering using different filters

表2 带噪信号信噪比10 dB情况下不同滤波算法结果对比Tab.2 Comparison of filtering results of noisy signal with SNR of 10 dB using different filtering algorithms

表3 不同带噪信号信噪比下不同滤波算法结果对比Tab.3 Comparison of filtering results of noisy signal with different SNR using different filtering algorithms
4 现场应用
某公司的连续波MWD,该钻井液连续压力波信号采用QPSK编码方式。如图12所示,该原始信号频谱中心频率为12~19 Hz,与中心频率接近的泵噪声12 Hz、18 Hz、35 Hz,高频随机噪声频率在50 Hz以上,低频噪声频率范围为0~10 Hz。噪声分布广且与有用的钻井液连续压力波信号频谱相混叠。通过新方法滤波后,输出波形的频谱(图13)中低频率噪声0~10 Hz、与中心频率接近的泵噪声12 Hz、18 Hz、35 Hz 的高频信号、50 Hz以上的随机高频噪声得到了更大程度的抑制,有用的钻井液连续压力波信号得到了更好的复原。

图12 原始钻井液连续压力波信号频谱分析Fig.12 Spectrum analysis of original continuous pressure wave of drilling fluid
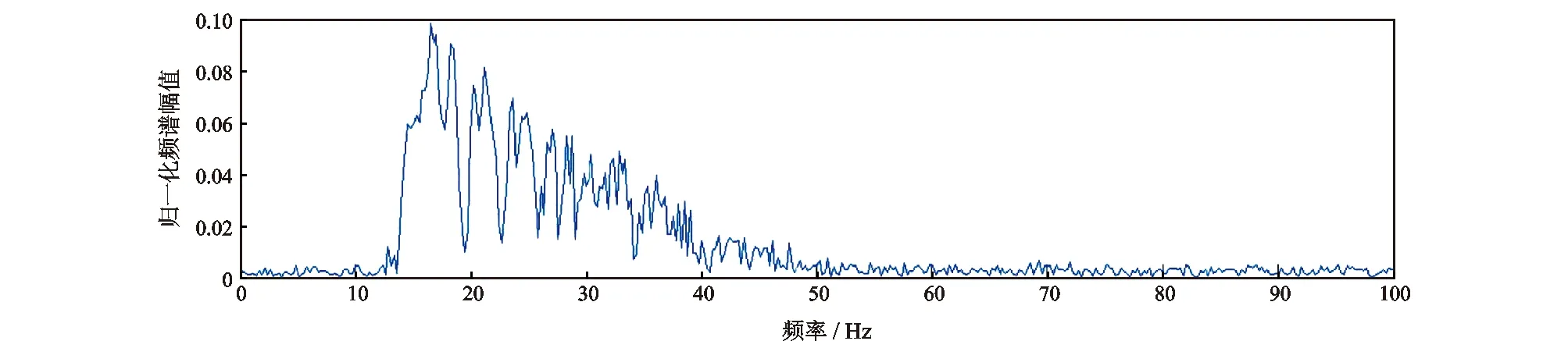
图13 钻井液连续波滤波后波形频谱Fig.13 Spectrum analysis of continuous pressure wave of drilling fluid after filtering
自适应变步长滤波算法性能对比如图14所示。由于该算法在计算起初误差大,步长调整为较大值,加快了收敛速度,而当滤波算法误差较小时,步长调整为平稳的较小值,保持了平稳收敛误差。相比其他算法,自适应变步长滤波算法缓解了收敛速度与稳态误差之间的矛盾,取得了良好的结果。
钻井液连续压力波信号在不同信噪比下,自适应滤波、小波分解、CEEMD、新方法的误码率见表4。固定参数滤波算法误码率在22%以上,新方法误码率在11%以下。特别在低信噪比的情况下,新方法的误码率远低于固定参数滤波算法,证明了该方法在钻井液连续波信号检测和识别上的优越性。
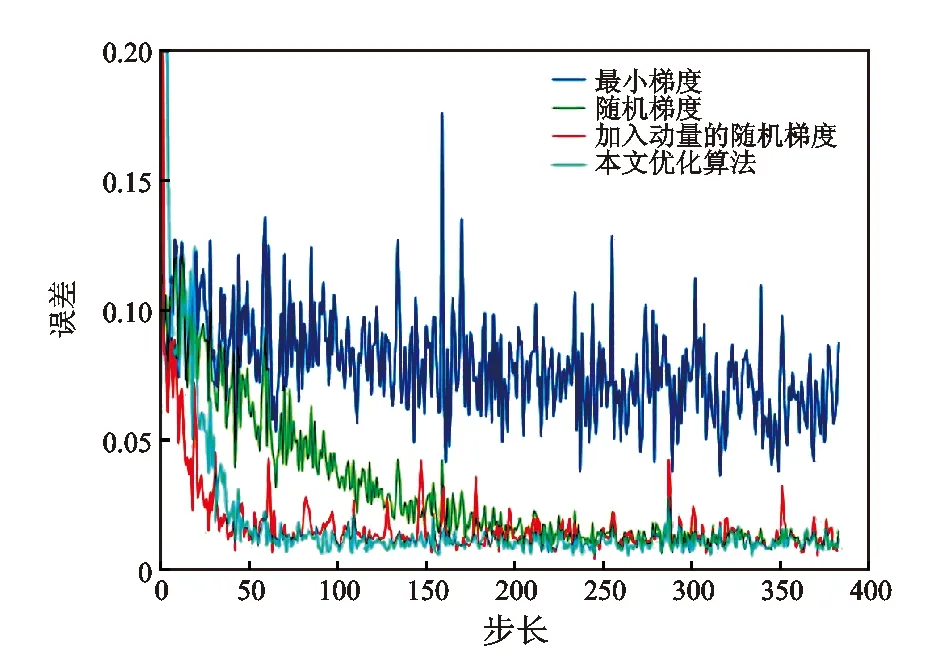
图14 优化算法性能比较Fig.14 Performance comparison of optimization algorithms

表4 不同信噪比下不同滤波算法的误码率Tab.4 Bit error rate of different filtering algorithms under different signal-to-noise ratios
5 结束语
针对固定参数滤波器在钻井液连续压力波信号滤波上的问题,提出了基于小波包变换结合自适应变步长 RBF神经网络非线性滤波器的信号滤波方法,该方法发挥了小波包变换分辨率高、RBF神经网络逼近性能强、自适应变步长滤波算法精度高、实时性好的优势。
通过仿真验证和实际现场应用表明:相比固定参数滤波算法,新方法提高了滤波器收敛速度,降低了稳态误差,误码率小于11%,具有较高的实用价值。在较低信噪比情况下,该方法在提升信号信噪比方面有明显优势,能够实现连续压力波信号检测和识别。
