结合图像增强的含噪齿轮图像边缘检测研究*
2021-08-07肖文韬李登峰
肖文韬,李登峰
(武汉纺织大学 数学与计算机学院, 湖北 武汉 430200)
0 引 言
齿轮是现代工业生产中最重要的零部件之一。在齿轮的批量生产中,对其进行缺陷检测和后期故障检测具有重要意义。
图像的边缘对于人类视觉而言具有重要意义[1],同时边缘检测作为视觉测量的基础,其结果直接影响到图像特征及平面几何参数测量的精度[2]。Canny算子、Sobel[3]算子和LOG算子等目前常见的传统边缘检测算法具有易实现、应用广泛等特点。
由于图像噪声和边缘都属于高频信号,导致传统边缘检测算子对于噪声较为敏感,难以区分边缘和噪声[4],对图像真实边缘的检测不理想。而在傅里叶变换基础上发展而来的小波变换,与傅里叶变换相比,其在时间域和频域内处理信号方面有较强的优越性[5],因此,在图像处理等方面有非常多的应用[6]。
文献[7]提出了一种融合小波变换模极大值法和多尺度多结构形态学的图像边缘检测算法,并采用该算法对电力机房的图像进行了处理。文献[8]认为由于数据噪声的存在,在漏磁内检测会导致边缘检测精度大大降低,提出了一种基于数据融合的小波变换漏磁异常边缘检测方法。
由于采用视觉技术检测齿轮的第一步就是对工业齿轮图像的采集,避免不了混合噪声的混入,进行图像去噪的预处理,再进行边缘检测是其中必不可少的一步。文献[9]将非局部均值算法与字典算法相结合,通过建立字典集的方式减少了领域搜索操作。文献[10]将大津法与分数阶微分滤波器相结合,设计了图像去噪与增强算法。
综合上述的分析可知,在对齿轮图像边缘进行检测过程中,齿轮图像边缘信息易受外界环境因素干扰,在对齿轮图像进行去噪预处理时,传统边缘检测算法难以满足其去噪效果;并且无法尽可能地保留更多的真实边缘。
而尽可能保留更多真实边缘也是齿轮边缘检测的关键。因此,本文提出一种结合图像增强的含噪齿轮图像边缘检测算法,对该算法的去噪效果和边缘检测效果进行研究。
1 滤波算法
1.1 自适应中值滤波器
中值滤波器是一种常见的非线性滤波器。在图像的处理过程中,中值滤波器窗口尺寸大小固定,因此,它不能在去噪的同时,更好地保留图像的细节。
而自适应中值滤波器(AMF)通过动态的调节窗口尺寸,可以将窗口内像素点灰度值按顺序排列,获取排序后的中值代替所检测到的目标噪声像素点灰度值,同时还可以达到去噪和保护细节的效果。
AMF的处理过程主要有两个步骤。其算法的变量有:Zmin(窗口领域内最小像素值)、Zmed(窗口领域内像素中值)、Zmax(窗口领域内最大像素值)。AMF的具体处理过程如下:
步骤1:A1=Zmed-Zmin,A2=Zmed-Zmax。如果A1>0且A2<0,则进入步骤2,否则增大窗口尺寸ns;如果窗口尺寸ns≤nmax,则继续步骤1,否则直接输出Zmed;
步骤2:B1=f(i,j)-Zmin,B2=f(i,j)-Zmax。如果B1>0且B2<0,则输出f(i,j),否则输出Zmed。
1.2 马氏距离
随着图像处理技术的发展,像素间距离的定义及计算方式逐渐增多,欧氏距离和曼哈顿距离经常被应用到图像处理中,而马氏距离作为一种能够有效地计算未知样本集的相似度方法,已经逐渐出现在研究者的研究内容中。
马氏距离主要对样本数据进行标准化处理,排除变量之间的相关性干扰,可以有效地衡量样本之间的相似度[11],克服了欧式距离存在的不足。
马氏距离的定义如下:

(1)
(2)
可得两组样本数据之间的马氏距离为:
(3)
1.3 改进自适应中值滤波器
从式(3)中可以看出协方差S会出现逆矩阵不存在的情况,针对逆矩阵不存在问题,有研究者采用奇异值分解去解决,并提出了马氏距离公式,如下[13]:
(4)
式中:λ1—图像块中有用信号的方差。
综合上述分析,本文引入信息熵来替代λ1,信息熵作为一个信息含量的量化指标,可以反映图像中有用信息的丰富程度。
信息熵公式如下:

(5)
将式(5)引入马氏距离公式,解决了式(4)复杂的推导和马氏距离协方差逆矩阵不存在现象,同时由于图像信息熵各不相同,使得新的马氏距离公式具有不错的自适应性。
改进后的马氏距离公式如下:
(6)
相关研究已经表明,中值滤波器对脉冲噪声去噪效果较好,对高斯噪声去噪效果较差,现将改进的马氏距离公式用于改进自适应中值滤波器,使其对混合噪声去噪具有不错的效果,并采用本文权值公式确定权值,步骤如下:
(1)采用AMF对原图像f(x,y)去噪预处理得到一组样本数据xj;
(2)定义模板窗口T从n=3开始增加,最大nmax=7,窗口内最大像素值为Tmax、最小像素值为Tmin和中值Tmed;
(3)若Tmin (4)根据权值系数和式(7)计算f(x,y)所对应的权重。 本文的权值公式定义如下: H(i,j)=1/(1+hi) (7) (5)若满足步骤3中的判断条件,则根据式(7)得到最终输出像素值,否则输出像素值f(i,j)=Tmed。最终输出像素值公式如下: (8) 幂次变换和对数变换都是对图像整体明亮程度进行一种非线性变换。 图像的幂次变换基本公式如下: I(x,y)=c[f(x,y)]γ (9) 式中:f(x,y)—原始图像;I(x,y)—幂次变换后图像;c,γ—正常数。 当γ>1时,效果为放大原始图像亮区细节。当0<γ<1时,效果为放大原始图像中低像素值区的灰度值,压缩高像素值区的灰度值,从而增强暗处细节。 根据上述分析,通常令c=1,而γ值却无法自适应确定。因为图像均值和信息熵与图像性质具有很大关联,结合图像的均值和信息熵来自适应确定γ值,其具体步骤为: (1)将原图像根据图像均值映射到模糊域: (10) (2)根据公式(5)信息熵确定γ1值,公式如下: (11) (3)得到自适应幂次变换为: F(x,y)=[f(x,y)]γ1 (12) 其中:γ1∈[0,1]。 基于Retinex理论的算法是图像增强领域应用最为广泛的算法之一,其主要分为两类算法:单尺度Retinex算法和多尺度Retinex算法。该算法不但可以弥补光照不均匀对图像的影响,而且可以增强整体图像的对比度,但存在容易使图像失真的问题[14]。 因此,根据Retinex理论,可以将一幅图像的数学模型描述为: F(i,j)=L(i,j)·R(i,j) (13) 式中:R(i,j)—反射分量;L(i,j)—照度分量。 其具体步骤如下: (1)利用取对数的方式将分量分离,可得到: logF(i,j)=logL(i,j)+logR(i,j) (14) (2)得到单尺度Retinex算法(SSR)模型为: R(i,j)=logF(i,j)-log[I(i,j)*L(i,j)] (15) 式中:*—卷积算子;I(i,j)—高斯卷积函数。 (3)将自适应幂次变换代替对数变换求解分量,具体模型如下: R(i,j)=[F(i,j)]γ1-[I(i,j)*L(i,j)]γ2 (16) 其中:γ1、γ2均由公式(3)自适应确定。 最后,对R(i,j)取反对数,可以得到增强后的图像f(i,j)。 小波模极大值法边缘检测就是利用一个平滑函数的导数作为小波变换的高频基函数[15]。 其具体过程描述如下: (17) (2)运用高斯平滑函数对图像f(i,j)进行卷积处理,可得: (18) (19) (3)设在尺度s下,图像的梯度幅值为Msjf(i,j),幅角为Asjf(i,j),则有: (20) (21) 传统小波模极大值法阈值的选取为单一阈值,而在进行边缘检测时,高低阈值的选取直接影响到真实边缘的检测。由于边缘检测的起始点往往由高阈值控制,如果高阈值越小,虽然边缘信息保留的更多,但是伪边缘和噪声也会变多。 因此,本文根据梯度图像灰度值所在比例来得出高阈值,具体过程如下: (1)采用直方图统计法,对式(20)所得梯度图像进行灰度值统计,得到S(h),h∈[1,255]; (2)遍历直方图,统计每个像素值所占比例,得到公式如下: (22) (3)定义本文判断方式,若p≥0.6*MN,且p≤0.8*MN时,灰度值定义为高阈值。其中:MN—图像大小; (4)选取高阈值的40%作为低阈值。 图像质量评价客观法通过测量相关指标,定量模拟人类视觉系统对图像质量感知效果[16]。因此,为了更好地验证去噪实验的结果,本文选取可观评价指标PSNR(峰值信噪比)、SNR(信噪比)和SSIM(结构相似度)作为实验评价指标。 具体的实验结果如下: 加入0.5%高斯噪声和1%椒盐噪声检测齿轮图像去噪实验结果,如图1所示。 图1 齿轮图像去噪实验 加入0.5%高斯噪声和1%椒盐噪声检测齿轮图像去噪实验客观评价指标结果,如表1所示。 表1 客观评价指标值 加入0.5%高斯噪声和1%椒盐噪声检测齿轮图像用传统Canny边缘检测实验结果,如图2所示。 图2 传统Canny算子边缘检测 图1、表1和图2的实验结果表明:当加入0.5%高斯噪声和1%椒盐噪声验证齿轮图像去噪效果时,本文改进的自适应中值滤波具有更好的去噪效果;同时,采用传统Canny边缘检测算法验证去噪后的检测效果也表明本文的去噪效果明显,客观评价指标最高。 笔者截取上述齿轮图像的局部图像进行像素级边缘检测,同样地加入0.5%高斯噪声和1%椒盐噪声,用以验证亚像素精度,其结果如图3所示。 图3的实验结果表明:本文算法获取的局部齿轮边缘图像连续性良好,去噪效果明显。 图3 局部齿轮图像边缘检测实验 加入3%高斯噪声和2%椒盐噪声检测齿轮图像边缘检测实验结果,如图4所示。 图4 齿轮图像边缘检测实验 图4实验结果表明:加入高浓度噪声后,对去噪后的图像进行Retinex算法处理,对噪声起到了一定的抑制效果。但是由于原图并非低光照图像,齿轮表面本身就粗糙,对比度和亮度增强后,齿轮表面的部分混合噪声和特征点被放大,从而使得其表面噪声被当作虚假边缘检测出来。 这一不足也与本文小波采取的自适应阈值选取有关,对于边缘检测阈值的选取也将是以后的研究内容。 为了提高齿轮后期故障检测和缺陷检测效果,并在一定程度上去除图像中的混合噪声,笔者提出了一种结合图像增强的含噪齿轮图像边缘检测算法;首先利用马氏距离和自适应权值公式,改进了自适应中值滤波器;然后改进了Retinex算法,并将图像增强理论引入到齿轮图像边缘检测中,提升了边缘细节和去噪效果;最后采用小波模极大值法进行了边缘检测。 实验及研究结果表明: (1)将马氏距离用于自适应中值滤波器的改进,使其对低浓度混合噪声具有良好的去噪效果,引入Retinex算法来增强边缘细节信息,同时一定程度上抑制了噪声; (2)在低浓度噪声时,采用本文算法对齿轮图像边缘进行检测能够获得完整清晰的边缘,像素级边缘连续;在高浓度噪声时,采用本文算法对噪声也有一定的抑制效果。 在下一阶段,本研究将人工采集低光照图像进行亮度及对比度增强实验。由于距离公式的引入,时间复杂度有所增加。因此,后续笔者将把算法效率作为研究的重点。
2 幂次变换结合Retinex算法
2.1 自适应幂次变换
2.2 改进的Retinex算法
3 小波模极大值法边缘检测
3.1 传统小波模极大值
3.2 改进阈值选取方式
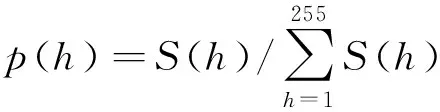
4 实验结果及其分析






5 结束语
