基于HEI量化故障信息的行星齿轮箱故障诊断方法研究*
2021-08-07李宇恒蒋章雷毕浩程
李宇恒,蒋章雷,梁 好,毕浩程
(北京信息科技大学 现代测控技术教育部重点实验室,北京 100192)
0 引 言
在全球的风电机组累计装机容量快速增长的背景下,由部件故障导致的机组停机事故频发。其中,造成停机最大时间的故障主要集中在风电机组的齿轮箱传动系统[1]。由此可见,齿轮和轴承是风电机组故障高发部件。因此,对风电机组发生各种异常状态或故障进行及时、有效的监测是非常必要的。
风力发电机组的传动系统多采用行星齿轮箱,且行星齿轮箱结构复杂、运行工况多变,齿轮啮合特征频率、零部件的旋转特征频率、故障特征频率等多个频率之间存在着大量的耦合情况。故对行星齿轮箱的故障特征提取一直存在着很大的困难。如今,行星齿轮箱的状态诊断、趋势预测研究及相关研究已成为国内外科学研究中的一个热点课题。
秦嗣峰等人[2]提出了基于Vold-Kalman滤波和高阶能量分离的方法,准确识别了信号中的时变频率成分,解决了频率离散的行星齿轮箱振动信号单分量分解问题。祝文颖等人[3]提出了迭代Hilbert变换与Fourier变换相结合的信号解调分析方法,实现了对敏感分量的幅值解调和频率解调,提取出了行星齿轮箱振动信号中的故障信息,实现了对行星齿轮箱故障的准确诊断。隆勇等人[4]对平均后的振动信号进行了加窗分离;然后,对分离的振动信号进行了VMD分解,并选取了包含故障的特征分量;最后,对选取的特征分量进行了Hilbert解调分析,实现了行星轮故障特征提取。刘一鸣[5]根据齿轮箱振动信号中故障成分与平稳啮合成分在形态上的差异,采用了基于可调品质因子小波字典的稀疏分解方法对信号中的故障成分进行了提取,形成了风电机组多故障诊断方法。李肖等人[6]为了准确提取行星齿轮箱组合故障特征,提出了基于变分模式分解的频率解调分析方法,根据中心频率和啮合频率的匹配关系选取了敏感单分量;通过分析敏感单分量瞬时频率频谱来诊断组合故障。马朝永等人[7]通过FSWT分解,重构了包含故障信息最多的频带,再对该频带进行FSWT-TT变换,提取了振动信号的故障特征。乔新勇等人[8,9]利用散布熵来实现VMD模态分量的选取,又把多尺度散布熵作为故障特征指标来实现故障诊断。武超等人[10]采用多点优化最小熵解卷积调整为原信号降噪,增强了信号中的周期性冲击成分,然后,通过包络谱实现了微弱故障特征的提取。
行星齿轮箱振动信号中频率情况复杂,难以直接对故障特征进行提取;通常对以啮合频率及其倍频为载波频率、故障特征频率等频率为间隔的边频带进行分析,实现故障特征提取;不能直接通过故障特征频率的出现来实现行星齿轮箱的故障诊断。
综上所述,本文提出基于谐波有效指数(HEI)量化故障信息行星齿轮箱故障诊断方法。首先,笔者对信号进行分析处理,对FSWT频率切片后的频带信号进行RCMDE值计算,选取故障特征多的频带进行信号重构,然后使用MOMEDA对重构信号中的故障冲击成分进行准确提取,再采用谐波有效指数量化处理信号中携带的故障信息,并通过该指标确定行星齿轮箱全寿命周期实验中,振动信号中包含的故障信息,实现对行星齿轮箱的故障诊断。
1 信号处理算法的基本理论
1.1 频率切片小波变换
令L2(R)为有限向量空间(R为集合实数),对任意信号有f(t)∈L2(R),频率切片小波变换的定义以p(t)的傅里叶变换存在为前提[11],即:
(1)
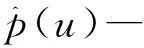
利用FSWT能方便地重构任意频带内的信号,对信号进行更加具体的分析。
1.2 精细复合多尺度散布熵
散布熵(DE)是一种表明时间序列复杂性和不规则程度的非线性动力学方法[12]。
(1)利用正态分布函数,将时间序列x={x1,x2,…,xN}映射到y={y1,y2,…,yN},y∈(0,1),即:
(2)
式中:μ―均值;σ―标准差。
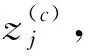
(3)
式中:c―类别数;int―取整函数。
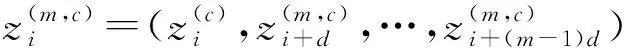
(4)
式中:m―嵌入维数;d―时延。
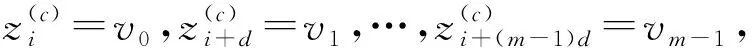
(5)计算所有散布模式πv0v1…vm-1的概率,即:
(5)
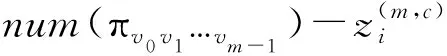
(6)根据香农熵的定义,则原序列的散布熵为:
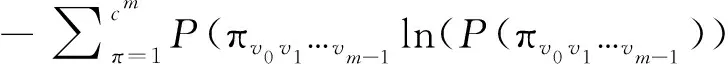
(6)
从散布熵的定义可知:当所有散布模式有相同的概率时,散布熵值最大,时间序列的越复杂,不规则程度越高;反之越低。
多尺度散布熵(MDE)是在散布熵的基础上,通过不同尺度反映时间序列的复杂程度。精细复合多尺度散布熵(RCMDE)是在MDE方法的基础上进一步细化,通过将原始信号按初始点分别为[1,τ]连续地分割成长度为τ的小段,并求其平均值得到τ个粗粒化序列来实现RCMDE计算的方法,其方式如下[13]:
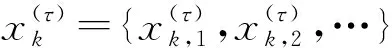
(7)

对于每个尺度τ,对应的RCMDE定义为:
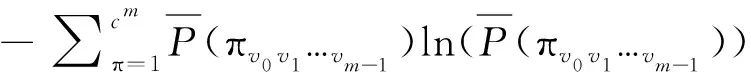
(8)

RCMDE解决了MDE粗细化过程中,部分统计信息易丢失的问题,减小了初始点选取对结果的误差影响,提高了计算精度。
1.3 MOMEDA算法
假设振动信号为x,可表达为[14]:
x=h*y+e
(9)
式中:y—冲击信号;h—系统频响函数;e—随机噪声。
为了实现对原始冲击信号的重构,减少噪声的影响,解卷积过程如下:
(10)
式中:N―采样点个数;L―滤波器大小。
其中:k=1,2,…,N-L。
考虑到故障脉冲周期性的特点,在这里引入了多点范数,即:
(11)
(12)
式中:t―目标向量,用于描述卷积目标冲击成分的位置和权重。
当目标向量t与原冲击信号y完全契合时,解卷积效果达到最佳;可以通过求解多点D范数的最大值来获得最优滤波器,此时的解卷积处理也可以获得最优解。
最优解可通过求解下式获得:
(13)
其中:f=f1,f2,…,fL;t=t1,t2,…,tN-L。
将式(10~12)代入式(13),可求得f作为一组最优滤波器,即:
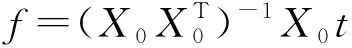
(14)
2 基于HEI的故障信息量化
2.1 HEI的提出
谐波乘积谱(HPS)是根据语音信号的短时谱来检测基音频率的方法。它可以通过将多个谐波的能量累计起来,寻求谐波乘积谱的最大值,来确定基音频率[15]。HPS的原理简单,对于某个频率ω,HPS被定义为其前N个谐波的幅值乘积,当ω恰好等于基本频率ω0时,突出的谐波幅值会进行相乘,幅值将急剧增加[16]。
基于此,谐波有效指数(HEI)被提了出来。它利用基本频率ω0谐波幅值的乘积,并进行标准化,来量化信号中包含故障脉冲的信息,即:
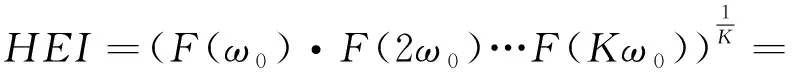
(15)
式中:F(ω0)―频谱图中ω0对应的幅值;K―谐频倍数。
HEI采用K次根运算来归一化谐波幅值的乘积,使得谐波的个数即使发生变化也可以有效表达故障信息。HEI的值与故障特征量成正比,与振动信号中包含的故障信息的丰富度成正比。
2.2 基于HEI的故障诊断流程
在实际工况中,受到噪声的干扰,行星轮故障特征频率更加难以直接在行星齿轮箱的振动信号的频谱中识别。
由于故障脉冲周期性出现的特点,笔者提出了基于HEI量化故障信息行星齿轮箱故障诊断方法。其具体的步骤如图1所示。
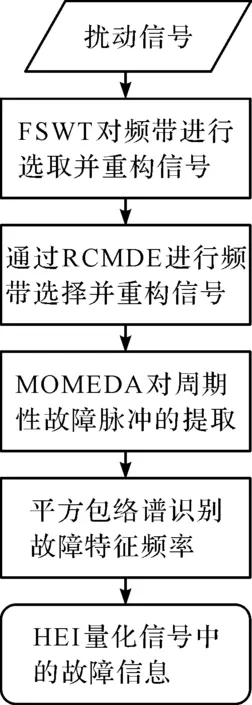
图1 故障诊断流程图
(1)对原始信号进行FSWT分析,将信号划分为不同频带的子信号,通过精细复合多尺度散布熵,对子频带信号进行分析;参考信号在不同尺度因子下值的差异,选取合适的尺度因子下的作为指标;对包含故障信息丰富的频带进行选取,并进行信号重构,实现对信号的降噪;
(2)对重构信号进行包络解调,将故障信息从复杂的信号调幅部分中分离出来,得到低频调制信号;结合理论故障周期,选择合适的周期区间,使用MOMEDA算法有效提取出调制信号中的周期性故障冲击成分;
(3)通过平方包络谱突出信号中的瞬态能量成分,识别聚集在低频段的故障特征频率;利用谐波有效指数(HEI)对故障特征频率进行计算,量化信号中包含的故障信息,实现对行星齿轮箱的故障诊断。
3 试验和结果分析
笔者针对行星齿轮箱齿面磨损故障进行试验,以获取磨损故障全生命周期的振动数据。
实验台由行星齿轮箱、电机、制动器及其控制器、数据采集系统(加速度传感器、电涡流传感器等)组成,如图2所示。

图2 行星齿轮箱实验台
图2中:测点1~3处布置加速度传感器,测量振动信号:测点1对应行星齿轮箱第二级的位置(与水平方向成45°角);测点2、3分别对应第三级垂直和水平位置;测点4放置电涡流传感器,配合测速齿轮盘可得输出轴的实时转速。
行星齿轮箱参数如表1所示。

表1 行星齿轮箱各齿轮参数
G1—第一级行星轮;G2—第一级太阳轮;G3—第一级内齿圈;G4/G6—第二、三级行星轮;G5/G7—第二、三级太阳轮;G8—第二、三级共用内齿圈
各级齿轮的转频和啮合频率如表2所示。
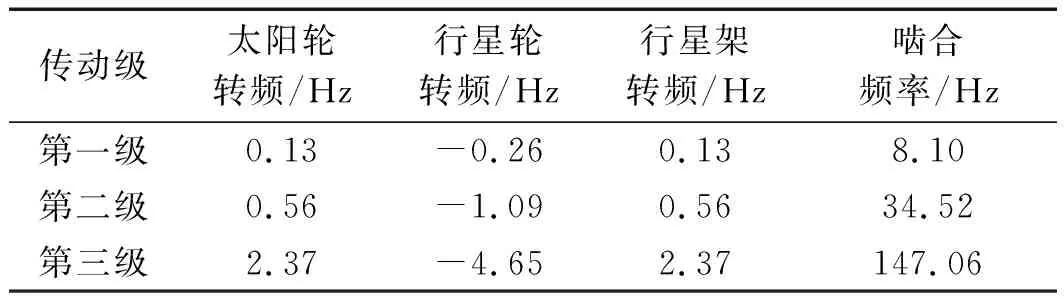
表2 齿轮转频及啮合频率
各级齿轮的故障频率如表3所示。
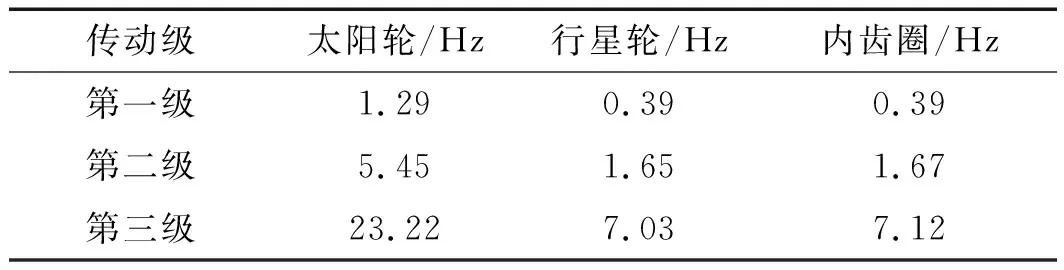
表3 各级齿轮故障频率
在该实验中,为了加快齿轮磨损的速度,笔者通过施加载荷和使用个别未经热处理的齿轮,来加快实验进度。实验中,采样频率设置为20 480 Hz,采样间隔为10 min,采样时间10 s;磁粉制动器转矩设置为8.33 N·m。
试验共持续9 300 min,本文分析数据采用测点2的振动信号。
3.1 基于RCMDE的信号降噪

根据行星齿轮箱故障演化机理可以得知:行星轮故障特征频率很大程度上会与啮合频率及其倍频参与耦合,而振动信号中正常状况下的啮合频率最为突出。因此,笔者使用FSWT对振动信号进行频率切片划分,分割间隔与啮合频率相近,为150 Hz。
振动信号的频率范围为0~9 900 Hz,笔者使用FSWT将信号频带划分为66组,得到其时域信号,如图3所示。
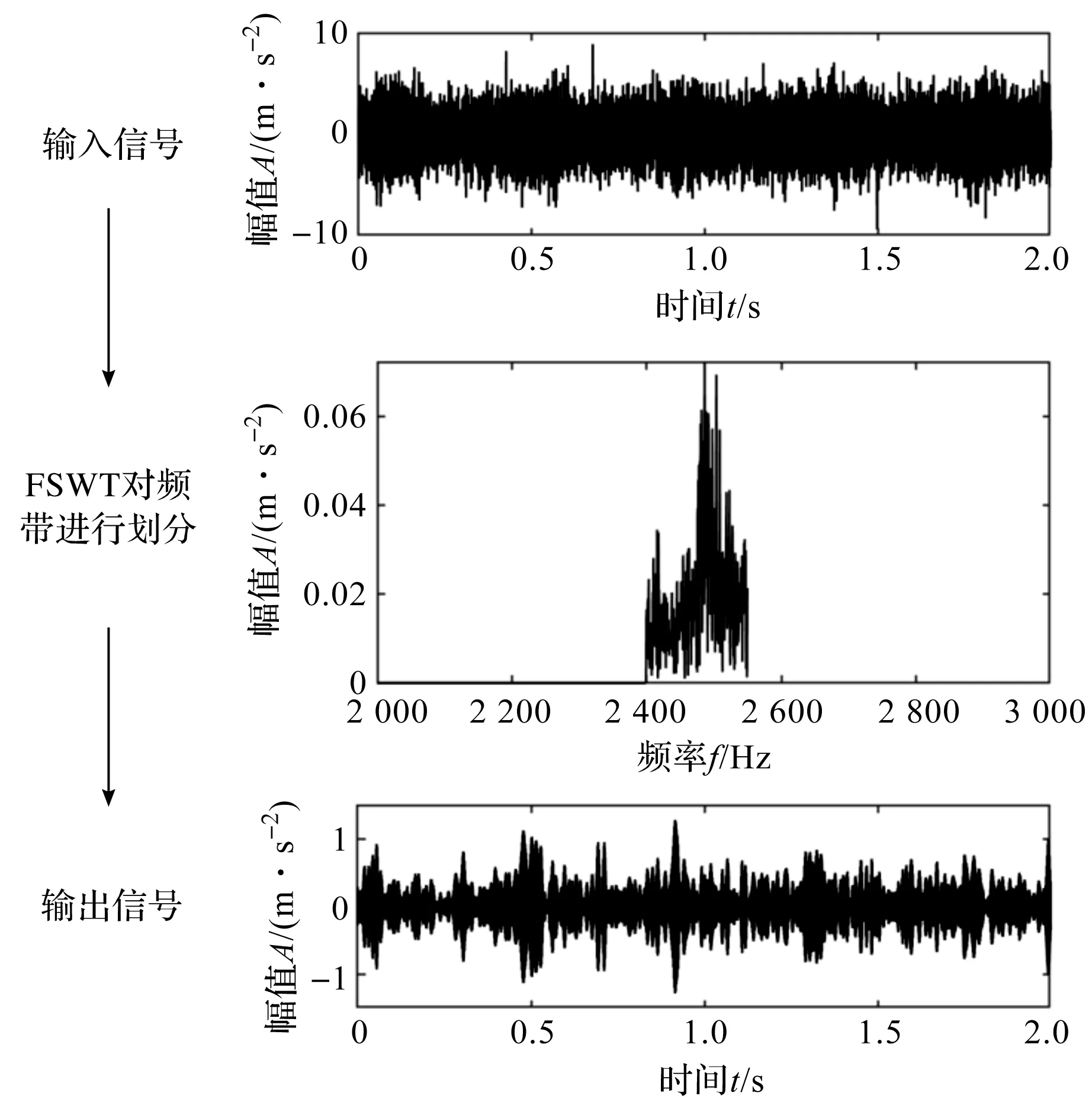
图3 FSWT对子频带信号的提取
图3为FSWT对第17组频带信号,即频率区间为2 400 Hz~2 550 Hz信号的提取方法。
将66组子频带的时域信号作为样本,对其进行RCMDE方法分析。设定其参数:嵌入维数m=3,类别c=3,时延d=1,最大尺度因子τmax=50。
在66组样本中,笔者任意选择3组进行RCMDE计算分析,如图4所示(图中所示为第9、18、27组样本数据在不同尺度因子下值的分析)。

图4 不同尺度因子下RCMDE值
从图4可以看出:3组数据熵值的整体变化趋势都大致相同;在低尺度因子范围内,其熵值较高,随着尺度因子的增加,熵值呈下降趋势,且逐渐趋于平稳。
对3组样本数据的ERCMDE值进行对比可以看出:在低尺度因子(τ<15)的情况下,不同样本数据在同一尺度因子的情况下,有明显的熵值区别和划分,整体熵值情况可近似为E09>E18>E27;在高尺度因子的情况下,不同数据的熵值在同一尺度因子或不同尺度因子的情况下都无明显差别;不同样本数据中包含的故障信息不可能完全相同,所以不同样本数据的ERCMDE值差异性越大,则对描述信号的故障程度更有效。
因此,该实例中笔者选取尺度因子τ=5、τ=10为计算样本数据的ERCMDE值的指标参数。
样本数据的ERCMDE值越高,则表明样本数据的复杂程度和不规则度越高,能量越分散,故障信息越少;反之,则说明信号中包含的故障信息越多。
笔者将尺度因子τ=5、τ=10对应的ERCMDE值作为指标,来衡量66组样本数据中包含的故障信息,如图5所示。
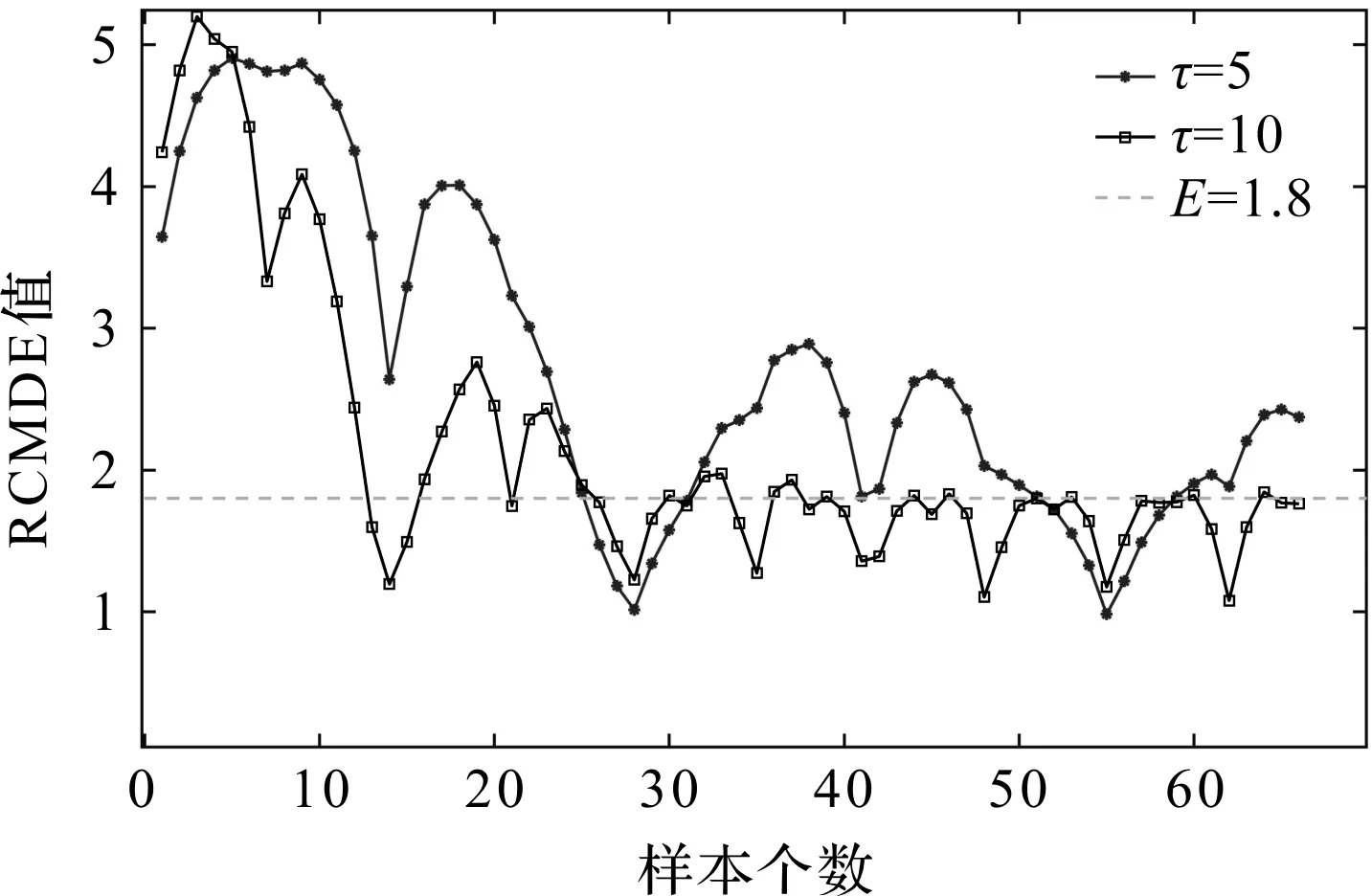
图5 65组样本数据的RCMDE值
笔者选取两种尺度因子下对应的66组样本数的ERCMDE进行分析;若样本同时在两种情况下熵值最小,则可以确定该样本数据中的故障脉冲所占比重越大。
笔者将ERCMDE=1.8作为选取频带信号熵值的临界值,将ERCMDE在两种尺度因子的情况下,同时小于1.8时的样本组进行提取,可以看出主要集中于样本组数为26~31区间和52~58区间,从中选取的频带数据如表4所示。
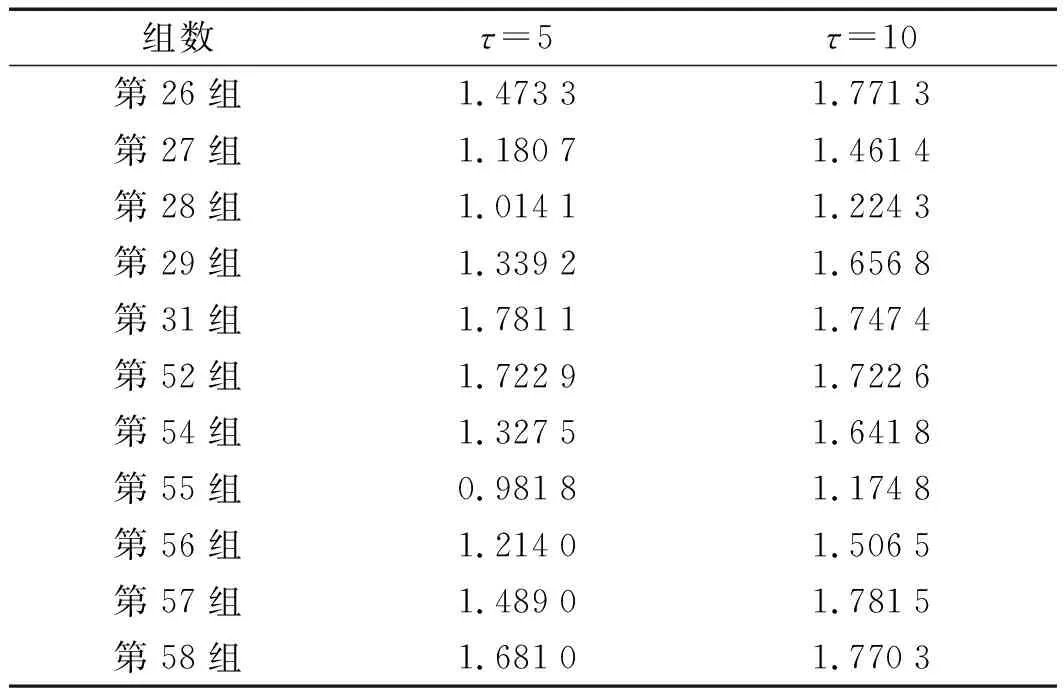
表4 所选频带信号的RCMDE值
将选取的11组频带信号进行叠加,可实现对信号的重构。由于行星齿轮箱的工况复杂,振动信号中存在多频率耦合情况;并且在FSWT信号分解过程中,原始信号中的某些谐波成分和噪声会分解为谐振频段。因此,对于重构信号中,仍然含有谐波分量和噪声成分,故障瞬态成分并不清晰。
笔者对重构信号进行包络解调,以将故障信息从复杂的信号调幅部分中分离出来,如图6所示。

图6 重构信号的包络谱
从图6中可以看出:最为明显的频率为行星轮齿轮箱的啮合频率fm=147.06 Hz;其次,较为突出的是行星架的转频fpc=2.37 Hz,行星轮故障特征频率fp=7.03 Hz及其倍频(3fp,7fp,10fp)。由此可以证明,采用RCMDE方法对信号进行重构,可以实现对信号的降噪,并将故障特征很好地突显出来。
同时,也可以看出:信号中存在很多其他频率,行星轮故障特征频率fp受到其他谐波和噪声的影响并不明显,故障瞬态成分和原始信号仍然没有很好地分离,需要进一步消除噪声,提取故障成分。
3.2 基于MOMEDA的故障特征提取
将重构信号进行Hilbert变换后,得到低频调制信号,再利用MOMEDA算法提取故障脉冲。

然后,笔者在多点峭度谱中选择在该区间峭度最大值处对应的周期,如图7所示。
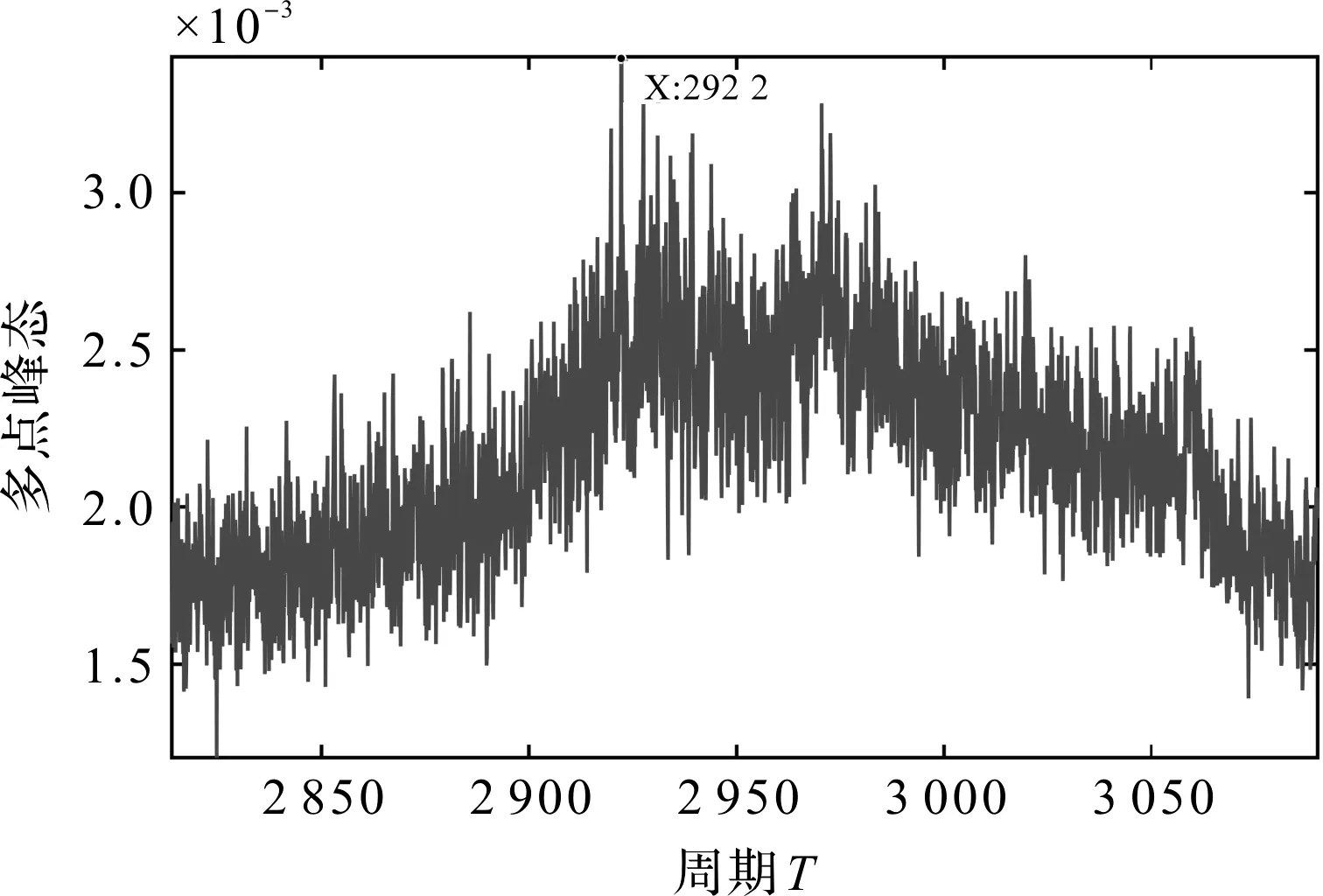
图7 多点峭度谱区间图
由图7可知:在周期T=2 922处的峭度值最大,此时的故障脉冲周期和理论脉冲周期的误差率为0.3%,故笔者所选择的故障脉冲周期为准确的故障脉冲周期。
笔者利用MOMDEA提取周期T=2 922的故障脉冲后的故障信号,对故障信号进行平方包络谱,将聚集在低频段的故障特征频率进行有效提取,如图8所示。

图8 故障信号的平方包络谱
从图8中可以清晰地看到行星轮故障频率fp及其倍频。由此可见,使用MOMEDA算法能够消除谐波分量和噪声等因素的干扰,准确提取故障信号中的周期性冲击成分;通过平方包络谱实现对行星轮故障特征的提取。
3.3 基于HEI量化的故障诊断
为了对故障信息进行精确计算,基于平方包络谱中得到故障特征频率fp及其倍频,笔者采用HEI来量化信号中包含故障脉冲的信息。
故障特征频率fp=7 Hz,nfp=7nHz(n—正整数),由于在实际分析中会存在微小误差,笔者在平方包络谱的频率区间[nfp-1,nfp+1]中取最大值,将前n个所选频率幅值相乘,并进行次根运算,即可得到谐波有效指数(HEI),将其作为故障谐波乘积谱指标,如图9所示。
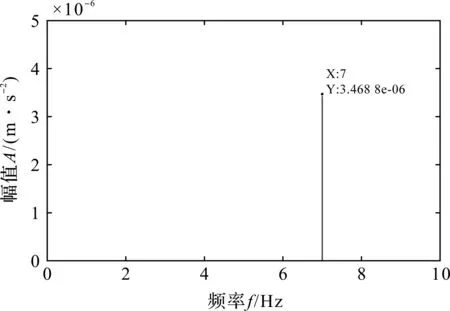
图9 故障谐波乘积指标
由图9可以看出,选定n=50后,所选数据中fp的HEI值为3.47×10-6。
分析行星轮故障演化机理可以发现:随着故障程度的增加,行星轮的故障特征频率会越发突出,而故障谐波乘积可以反映出故障特征频率在信号中的强度。因此,本文提出把HEI作为衡量故障程度的有效指标,可以有效量化信号中包含故障信息的强度。
4 结束语
本研究通过对振动信号处理方法的研究和分析,对行星齿轮箱故障特征进行提取,提出用谐波有效指数(HEI)来量化包含在信号中的故障信息的方法,并通过行星齿轮箱齿面磨损故障的试验对该方法进行了验证。
研究结果表明:
(1)通过利用RCMDE在不同尺度因子下ERCMDE值存在差异性的特点,对故障信号进行重构,不仅可以实现对信号的降噪,而且缩小了数据处理范围;
(2)使用MOMDEA和平方包络谱提取了行星齿轮箱的故障特征频率;基于HEI指标,将故障特征频率进行谐波乘积计算,有效量化了数据中包含的故障信息;
(3)解决了行星齿轮箱振动信号频率复杂、故障特征难以提取的问题,为衡量行星齿轮箱的故障程度提供了有效指标。
该研究方法涉及多种理论的应用,因此,今后的工作包括:
(1)对于RCMDE处理信号中的尺度因子和熵值的临界值ERCMDE的选取没有实现自适应,需要改进RCMDE中的参数,以实现其自适应优化;
(2)行星齿轮箱全寿命周期的磨损故障信息不一定呈上升趋势,需要对如何运用HEI指标描述行星齿轮箱系统故障的演变过程做进一步研究。
