自然光成像条件下植物根系图像的增强方法研究*

梁丽秀，裴玖玲，孙少杰，周 丹

（塔里木大学 机械电气化工程学院，新疆 阿拉尔 843300）

通过图像分割技术提取植物根系特征，是近年来植物根系研究中的重要技术手段，而在图像分割前对图像进行预处理是非常重要的一个环节，其目的是在提取目标区域之前先去除掉一些干扰信号，进而达到增强图片质量的效果，方便后续进行图像特征的提取及分析。本文以针对在自然光成像条件下水稻根系的图片为研究对象，如图1所示，因为水稻根系的特殊性和实验用于水稻生长的土壤环境限制，图像的边侧部位出现了不规则带状图，土壤颗粒及玻璃水印也会影响成像质量，复杂的环境造成了采集到的图像有较多的噪声点和条纹状的纹理，这些噪声和水稻自身众多根系在一起很难区分开来，使得采集到的图像普遍具有对比度低、噪声干扰大、纹理复杂等特点，想要完整、精确地对其进行分割面临很大困难。在分割之前对图像进行增强预处理，以便后续进行准确分割，这是极其必要的一环。本文采用多种图像增强方法，研究不同的图像增强方法对复杂环境成像条件的根系图像的增强效果。

图1 根系原图

1 直方图均衡化

直方图均衡化[1]的原理是利用累积函数来调整灰度图中的灰度值，进而全新分配图像中的像素值，拓宽比较窄的直方图，使密集分布的直方图通过非线性变换，转变为分布较为均匀的直方图，直方图均衡化的过程就是对像素变量的概率密度函数进行变换的过程，对于连续变化的灰度值，设变换函数为：

r是变换前的图像灰度，s是变换后的图像灰度值。T（r）在区间0≤r≤1中应为单调递增函数，并且当0≤r≤1时，0≤T（r）≤1。

Pr（r）是r的概率密度函数；Ps（s）是s的概率密度函数；Pr（r）和T（r）已知，所以有：

变量r的累积分布函数为：

由莱布尼茨准则：

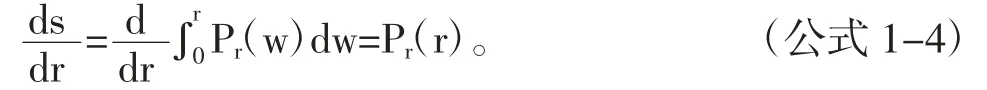
带入（公式1-2）中可得密度函数：

对于离散值：

其中：rk表示灰度级，k=0，1，2，…，L-1；nk是同一灰度级的像素个数；n为像素总数。

变换函数的离散形式为：

图2是对水稻根系图像的实验结果，由图可以看出，原图由于图像对比度偏低，根系细节和土壤难以分辨出来，经过直方图均衡后，由于根系图像的像素距离经变换后被拉大，使根系的细节得以突出显示出来，图像中可以较为清晰地看到水稻的根系轮廓，但同时土壤中的噪声点也突出显示出来了。

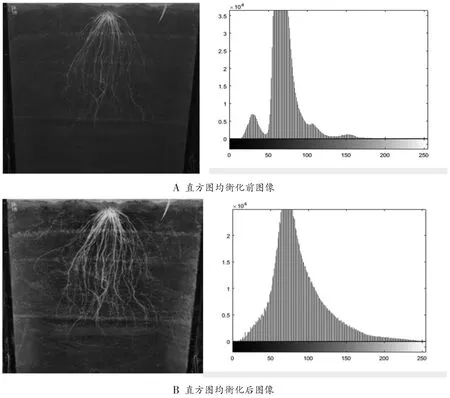
图2 直方图均衡化前后对比图

2 Frangi多尺度滤波

Frangi多尺度滤波器最初较多应用于医学领域的血管分割中，用于对血管和纺织图像的增强处理中[2-5]，水稻根系图像的特征与血管和织物图像的纹理特征有很多相似之处，其主体特征都是管状结构，尤其在末梢细小的部分相似的地方有很多，都是在对比度比较低的环境下进行分割处理，其要求都是要尽可能多保留细节特征。Frangi滤波器是利用Hessian矩阵原理对图像实现增强处理的，尤其适用于具有线性结构特征的图像提取。其原理是通过计算Hessian矩阵的特征值，而图像上像素如果发生了突变，那么该点像素与其相邻位置的像素就存在了差异，具有这种差异的像素点可以通过Hessian矩阵的特征值进行判断和寻找。对特征值函数进行分析，得出反映图像灰度像素在某点处的密度变化的趋势，从而找出突变位置。水稻的根系是线性结构，与背景之间存在明显的线性的边缘，利用Hessian矩阵来检测出图像中根系的边缘，进而将根系的线性结构提取出来，来实现对根系结构的增强效果。

利用高斯函数G（x，y）求出图像中每一个像素点的x和y方向上的二阶偏导：

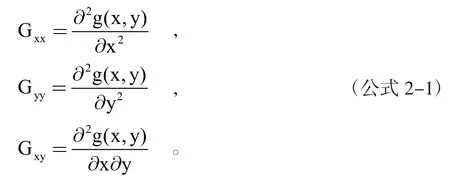
构造图像的Hessian矩阵H：

令λ1，λ2表示Hessian矩阵的特征值，|λ1|<|λ2|。计算出矩阵的特征值λ1和λ2，利用其构造出根系的增强函数，这里用两个特征值构造出两个变量S和Rb：

特征值都很小的地方多数是在背景点处，或和背景基本趋于一致的根系处，而特征值比较大的位置多数是在图像的灰度变化比较明显的地方，根系处的Hessian矩阵的特征值满足：Rb接近于零，S比较大；背景点处S比较小，Rb比较大。因此，可定义图像中点p是否属于根系的增强函数：

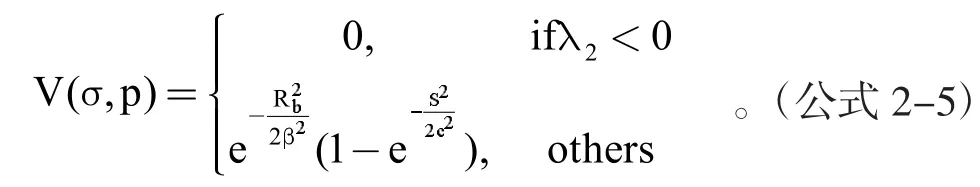
β和c分别是影响变量Rb和S的比例因子，其取值决定Rb和S灵敏性，由于水稻根系的直径大小不一，要对不同直径的根系进行尺度匹配，找到最大的响应度作为最终的输出，本文中β=0.5，c=15，由（公式2-6）计算出每个像素点增强后的最终像素值。

滤波器输出范围为0

图3 不同参数的Frangi滤波结果

在迭代步长step不变的条件下，尺度因子σ的取值越大对根系的增强效果在整体来看就越好，而在尺度因子σ不变的情况下，迭代步长step越小，在增强了细小的末梢根系的同时，也对图像中噪声的增强效果越强，为了更多地分割出细小的水稻根系特征，保留适当的噪声点是不可避免的，因此在不影响整体图像的增强效果的前提下，经过实验对比，尺度因子σ取值为[0.5 3.0]，迭代步长step取值为0.5的增强效果较为合理。

3 高斯滤波器

高斯滤波是一种线性平滑滤波器，纺织业和医学领域中的图像增强处理多采用高斯滤波器[6-7]。其滤波的原理和均值滤波器类似，核心就是对图像中的每一个像素进行过滤，过滤过程需设置一个卷积模板的窗口，该窗口的大小和参数值会直接影响到最终的滤波的效果，模板窗口的中心要高，边缘要低，也就是以模板的中心点为中心向外的数值是依次递减的。滤波时窗口扫描到的每一个像素，就用以该像素为中心的模板所确定的模板内像素灰度的加权平均值去代替中心的像素值。常用的高斯模板有如下几种形式：左侧是3×3的模板，右侧是5×5模板。而高斯函数适用于计算模板的系数。

高斯函数：

式中x和y是当前像素点的坐标，σ代表的高斯分布的标准差，标准差σ也是高斯滤波器的重要参数，是决定其平滑能力的一个重要指标，σ的取值与滤波器的平滑效果有很大关系。如果σ值较小，图像的平滑效果就不会很明显；若σ值较大，图像的平滑效果就会比较明显。通过调节σ的取值，就可以对图像的噪声和模糊程度起到抑制和均衡的作用。

本文以3×3的模板为基准，对根系图像进行平滑处理，图4为选取不同标准差σ下的实验效果对比图，由图可知，σ越小平滑效果不明显，图中σ取值分别为0.3、0.9和1.5时，根系图像增强效果并没有明显的变化。σ取值分别为2.0、3.0和5.0时，根系图像增强效果出现了明显的变化。σ取值越大对图像边缘和细节的增强效果越明显，会使根系的末梢变得更加模糊，根系细小的末梢很多已经看不到了，高斯滤波器可以抑制图像中环境引入的噪声点，但同时也会造成图像末梢细节特征的丢失。

图4 不同标准差的水稻根系高斯滤波结果

4 结束语

本文以自然光成像条件下的水稻根系的图片为研究对象，对具有较多的噪声点和条纹状的纹理的根系图像的增强处理进行研究分析，不同的图像增强方法对复杂环境成像条件的根系图像的增强效果不同，各有优缺点，经直方图均衡化增强后，根系的细节得以突出显示，图像中可以较为清晰地看到水稻根系的整体轮廓，但同时土壤中的噪声点也突出显示出来了。Frangi多尺度滤波高斯滤波在增强了细小的末梢根系的同时，也对图像中噪声的增强效果越强，在不影响整体图像的增强效果的前提下，为了更多地分割出细小的水稻根系特征，可适当保留一些图像中的噪声点。高斯滤波器可以抑制图像中环境引入的噪声点，但同时也会造成图像末梢细节特征的丢失。