基于有限元法的跌水闸闸室结构抗震安全复核研究

郭博文，鲁立三，王 荆，宋 力

（1.黄河水利科学研究院，郑州450003；2.水利部堤防安全与病害防治工程技术研究中心，郑州450003）

0 引 言

水闸是调节水位、控制流量的低水头水工建筑物，具有挡水和泄水（引水）的双重功能，在防洪、治涝、灌溉、供水、航运、发电等方面应用十分广泛。水闸一般由闸室段、上游连接段和下游连接段三部分组成。其中，闸室段是水闸控制水流最主要的部分，通常包括闸墩、闸门、底板、胸墙、岸墙、交通桥和工作桥等几部分。目前，我国具有的各种类型的水闸数量巨大，其中流量大于等于5 m3/s 的水闸数量就有105 283 座［1］。《水闸安全鉴定管理办法》［水建管（2008）214号文］规定，水闸工程在竣工验收后5年内进行首次安全鉴定，以后应每隔10年进行一次全面安全鉴定。

我国是一个多地震灾害国家，抗震安全复核是水闸安全鉴定的重要组成部分；同时，闸室结构作为水闸工程的咽喉部位，对水利枢纽工程安全性的影响尤为突出。因此，有必要对水闸闸室结构抗震安全复核进行研究。目前，大部分学者采用拟静力法对水闸结构进行抗震复核计算，事实上，水闸属于三维空间薄壁结构，如按照常规平面方法简化计算，会忽略闸底板、闸墩、启闭机房以及交通桥等建筑物之间的联系作用，计算结果误差较大［2］。近年来，随着计算机技术的快速发展，有限元数值模拟技术在水闸抗震分析中得到广泛应用［3］-［9］。因此，有必要采用三维有限元数值模拟技术对闸室结构进行抗震复核研究。

1 研究方法

1.1 振型分解反应谱法

本次采用《水工建筑物抗震设计标准》（GB51247-2018）［10］（以下简称抗震设计标准）中的标准设计反应谱对闸室结构进行抗震复核计算，具体如图1 所示，其中阻尼比取7%，反应谱最大值的代表值βmax取为2.25。

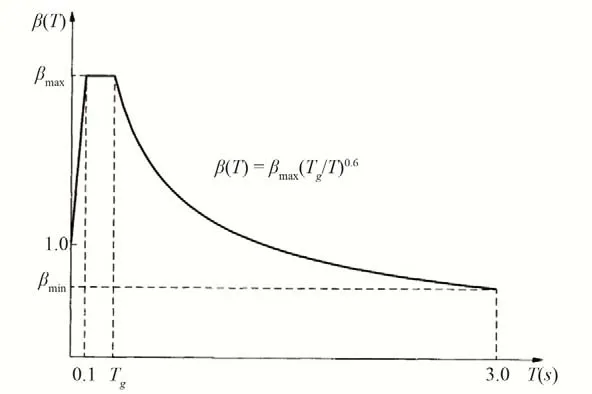
图1 标准设计反应谱

根据抗震设计标准的规定，采用振型分解反应谱法计算地震作用效应时，可由各阶振型的地震作用效应按平方和方根组合。当两个振型的频率差的绝对值与其中一个较小的频率之比小于0.1 时，地震作用效应宜采用完全二次型方根组合，具体计算公式如下：

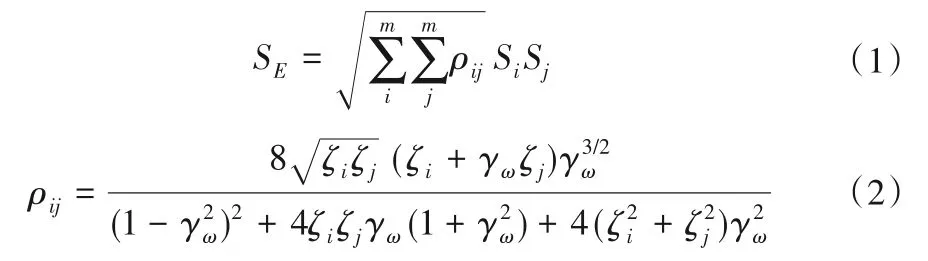
式中：SE为地震作用效应；Si、Sj分别为第i阶、第j阶振型的地震作用效应；m为计算采用的振型数；ρij为第i阶、第j阶振型的振型相关系数；ζi、ζj分别为第i阶、第j阶振型的阻尼比；γω为圆频率比，γω=ωj/ωi；ωi、ωj分别为第i阶、第j阶振型圆频率。

考虑到地震的往复性，由反应谱法得到的位移、应力等响应指标可正可负。因此，在进行结构响应的动静力叠加时，本次计算采用的叠加原则为：①静力计算结果直接加上反应谱计算结果（简称，静+动）；②静力计算结果直接减去反应谱计算结果（简称，静-动）。

1.2 拉应力复核

目前，如何对有限元计算结果中拉应力超过混凝土轴心抗拉强度标准值区域进行安全评价还研究较少，本文采用有限元数值模拟与结构力学计算相结合的方法对拉应力进行复核。总结开敞式水闸有限元抗震复核结果不难发现，受地震作用影响，闸墩与闸底板相交处易出现较大拉应力区，该区域拉应力一般会超过混凝土动态轴心抗拉强度标准值。地震作用下，闸墩为偏心受压构件，为安全考虑，考虑最不利情况，闸墩按纯弯构件考虑。

依据《水工混凝土结构设计规范》（SL191-2008）［11］中正截面受弯承载力计算相关内容，矩形截面或翼缘位于受拉边的倒T形截面受弯构件，其正截面受弯承载力应符合下列规定：

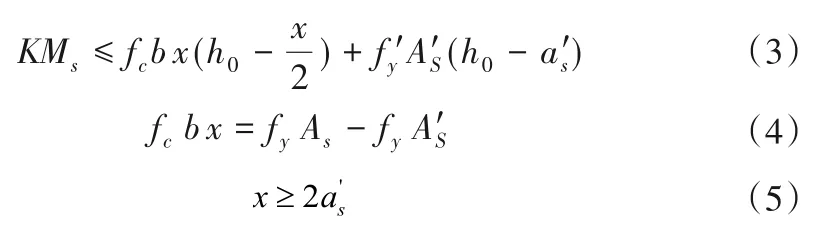
式中：K为承载力安全系数；Ms为弯矩设计值，N·m；fc为混凝土轴心抗压强度设计值，Pa；As为纵向受拉钢筋的截面面积，m2；A'S为纵向受压钢筋的截面面积，m2；fy为钢筋抗拉强度设计值，Pa；f'y为钢筋抗压强度设计值，Pa；h0为截面有效高度，m；b为巨型截面的宽度或T形截面的腹板宽度，m；x为受压区计算高度，m；为受压钢筋合力点至受压区边缘的距离，m。

同时，对于纯弯构件，其截面上任一点处正应力的计算公式为：

式中：M为横截面上的弯矩，为得到截面上所能承受的最大正应力，此处M可取为Ms，N·m；Iz为横截面对中性轴z的惯性矩，m4；y为所求应力的点到中性轴z的距离，m。

将根据上述公式计算得到的应力结果与有限元计算结果进行对比，即可对拉应力超过混凝土动态轴心抗拉强度标准值区域进行复核。

1.3 抗滑稳定计算

根据《水闸设计规范》（SL265-2016）［12］，土基上沿闸室基底面的抗滑稳定安全系数按以下公式计算：

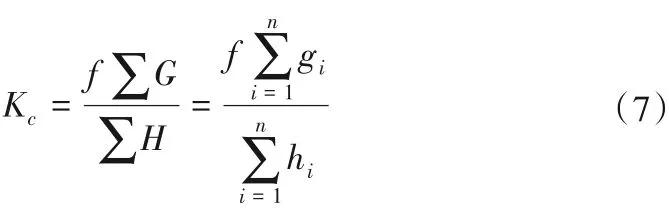
式中：Kc为抗滑稳定安全系数；f为基础底面与地基土之间的摩擦系数；∑G为作用在闸室上的全部竖向荷载，N；∑H为作用在闸室上的全部水平荷载，N；n为闸室底板节点个数；gi为第i个闸室底板节点上所受的竖向荷载，N；hi为第i个闸室底板节点上所受的水平向荷载，N。

2 有限元计算模型

2.1 有限元模型

某跌水闸工程共4 孔，为2 孔一联钢筋混凝土开敞式水闸，每联之间设置有分缝。闸室段总长度为12.50 m，闸室总宽度为47.45 m，边墩厚度为1.40 m，中墩厚度为1.40 m，缝墩厚度为1.85 m，每孔净宽为10.00 m。考虑到边墩两侧所受土压力和水压力的不同，本次计算主要对边孔一联跌水闸闸室结构进行计算分析。

根据跌水闸闸室结构实际尺寸，建立包括闸底板、闸墩、钢闸门、横梁和启闭机排架结构的边孔三维有限元模型，具体如图2 所示，模型共计48 802 个节点，34 825 个单元，全部采用八结点六面体单元进行空间离散。采用笛卡尔坐标系，横河向为X方向，顺水向方向为Y方向，铅直方向为Z方向，计算时闸墩和闸底板底部施加三向固定约束。需要指出的是，由于该枢纽工程已运行50余年，根据监测资料显示，地基沉降已基本稳定，同时，根据考虑地基时的初步试算结果，静、动力作用下闸室结构闸底板三向位移均较小，最大位移数值不足0.5 mm。因此，为便于分析计算，本次忽略地基的影响。

图2 某跌水闸边孔有限元模型

另外，由于跌水闸结构每孔闸墩上的公路桥和启闭机房是独立存在的，在相邻两节公路桥和启闭机房之间设置薄层单元，具体如图3 所示，在有限元计算中使薄层单元不参与运算，即可实现两节启闭机房之间以及公路桥之间的相对独立性。

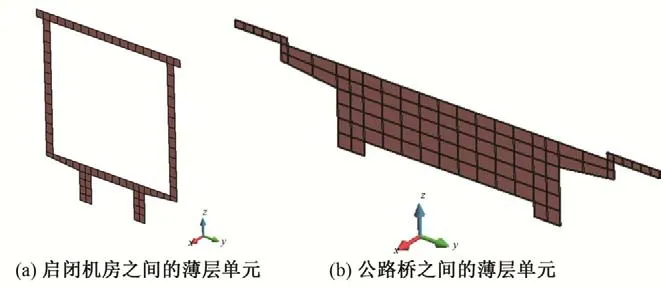
图3 跌水闸启闭机房之间以及公路桥之间的薄层单元

2.2 计算参数

本次计算中没有考虑钢筋单元，所有的混凝土单元代表的是素混凝土，为了体现钢筋的存在对混凝土弹性模量的影响，采用等效弹性模量来模拟钢筋混凝土的弹性模量。其中，在线弹性阶段，钢筋和混凝土是协调变形的，因此等效的原则如下：

式中：Ed为钢筋混凝土材料等效的弹性模量，GPa；Ec为素混凝土弹性模量，GPa；Es为钢筋弹性模量，GPa；As为钢筋截面面积，m2；A为混凝土截面面积，m2。

本次计算所采用的材料参数见表1。

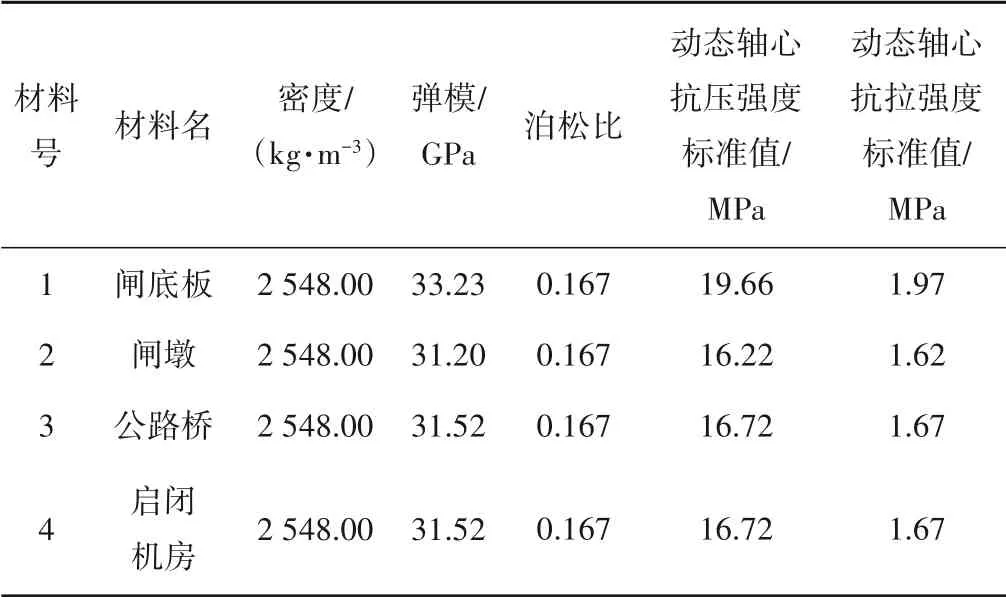
表1 混凝土材料参数

2.3 计算工况

本次计算工况为正常蓄水位运行期加Ⅷ度地震作用。其中，正常蓄水位运行时跌水闸闸室结构闸前水深4.03 m，闸后无水；Ⅷ度地震作用时地震动峰值加速度为0.20 g，地基反应谱特征周期Tg取0.35 s。

2.4 计算荷载

本次计算中主要考虑模型自重、水荷载、淤沙压力、浪压力、土压力、扬压力、风荷载、启闭机自重以及地震荷载等荷载作用。其中，扬压力由浮托力和渗透压力组成，渗透压力可采用改进阻力系数法计算。

3 有限元计算结果与分析

3.1 自振特性计算结果与分析

运用结构自振特性分析方法，考虑闸前水体对闸室结构的影响，对结构进行自振分析，得到跌水闸闸室结构前五阶频率、振型等自振特性参数，其中闸前水体对结构的影响采用Westergard的附加质量法进行模拟。正常蓄水位工况下跌水闸闸室结构前五阶自振频率和周期如表2 所示。从表2 中可以看出，在正常蓄水工况下跌水闸闸室结构自振的基频为4.038 Hz，且第二阶自振频率与基频数值相近，这主要是因为闸室结构每孔闸墩上的启闭机房是相互独立的，而闸室结构第一阶和第二阶振型分别为两节相互独立的启闭机房沿顺河向方向的振动。

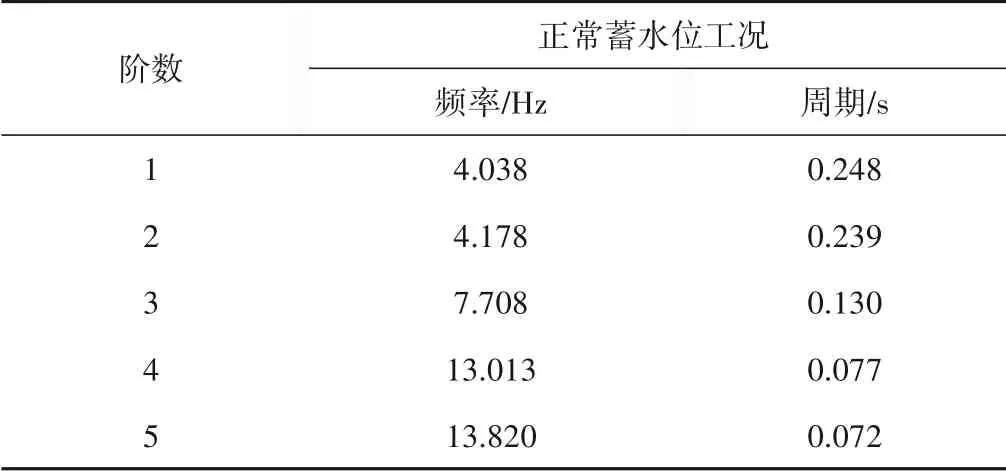
表2 不同工况下跌水闸闸室结构自振频率周期表

针对正常蓄水位工况，图4 给出了边孔闸室结构前五阶振型图。可以看出，跌水闸闸室结构前五阶振型主要体现为启闭机房和公路桥的振动，闸墩参与较少。

图4 跌水闸边孔闸室结构各阶振型图

3.2 位移计算结果与分析

图5 至图6 给出了动静叠加下边孔闸室结构在X向、Y向和Z向位移等值线图。由图5、6 可知，正常蓄水工况地震作用下跌水闸闸室结构位移在不同的叠加方式下最大数值分别为12.0 和10.0 mm，位置出现在启闭机房顶部位置，主要为顺河向位移。

图5 边孔闸室结构动静叠加（静+动）下位移等值线图（单位：m）

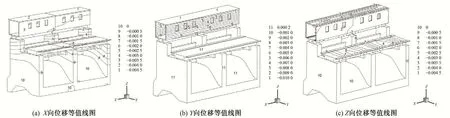
图6 边孔闸室结构动静叠加（静-动）下位移等值线图（单位：m）

3.3 应力计算结果与分析

图7 至图9 分别给出了动静叠加下跌水闸闸室结构各部位应力计算结果等值线图。可以看出，在正常蓄水位地震作用下，受地震作用影响，跌水闸闸墩与闸底板相交处出现了2.00 MPa 左右的拉应力，超过了跌水闸闸墩和闸底板混凝土动态轴心抗拉强度标准值（具体数值参照表1）。图10 给出了跌水闸边墩单位长度截面配筋图，基于2.2 节中所介绍的拉应力复核方法，根据式（1）至式（3）计算可得单位长度边墩横截面上最大承载弯矩为2 879.6 kN·m，由式（4）计算得到与跌水闸边墩与闸底板相交处能承受的最大拉应力为4.41 MPa，大于2.00 MPa，满足安全需求。

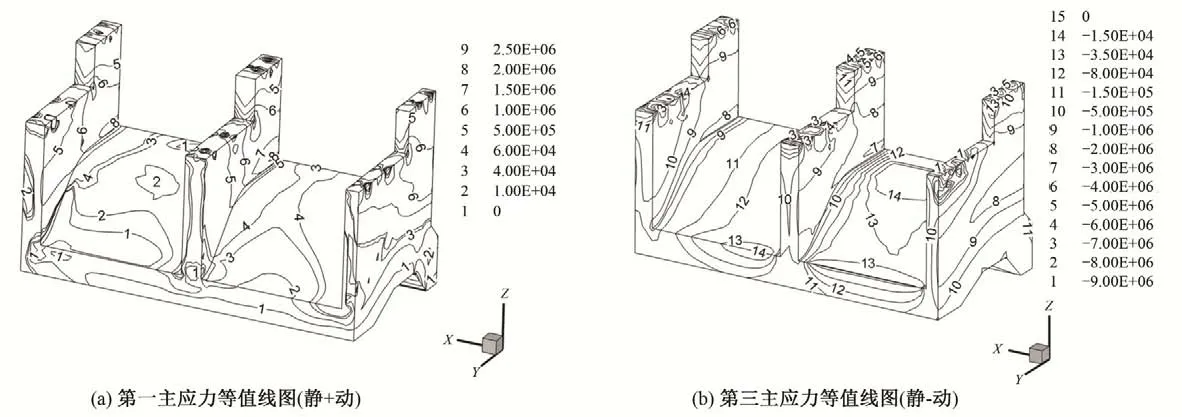
图7 跌水闸闸墩和底板结构主应力等值线图（单位：Pa）

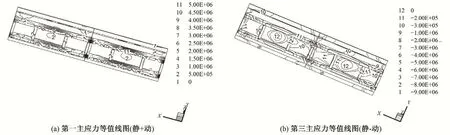
图8 横梁动静叠加下主应力等值线图（单位：Pa）

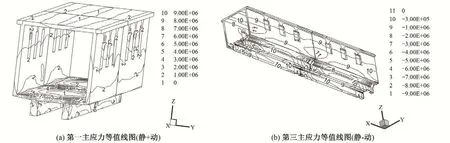
图9 机架桥动静叠加下主应力等值线图（单位：Pa）

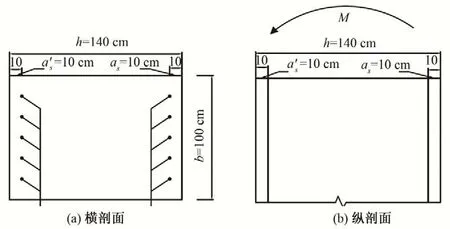
图10 跌水闸边墩单位长度截面配筋图

受自身重量、公路桥荷载以及地震作用影响，跌水闸公路桥跨中底部位置处出现了较大拉应力区，其数值达到了5.00 MPa 左右，远超跌水闸公路桥混凝土动态轴心抗拉强度标准值，考虑到跌水闸公路桥运行时间较长，且桥梁底部钢筋混凝土也出现脱落、露筋和胀裂等情况，具体如图11所示，应对跌水闸公路桥进行相应的抗震处理措施。另外，受地震作用影响，启闭机底板部分区域出现了8.00 MPa 拉应力区，为安全起见，宜采取相应的抗震加固措施。

图11 跌水闸桥梁底部混凝土脱落、漏筋和胀裂现象

同时，机公路桥和启闭机房与闸墩联结位置处有较大压应力区，最大压应力数值达到了9.00 MPa 左右，未超过跌水闸闸墩、公路桥和启闭机房混凝土动态轴心抗压强度标准值，满足安全要求。

3.4 稳定计算结果与分析

表3 给出了动静叠加下跌水闸闸室结构抗滑稳定计算结果。由表3可知，根据有限元动力计算结果，作用在边孔闸室上的水平向地震荷载为2 863.72 kN。由于地震作用是随机往复的，当该水平向地震惯性力朝下游时，结合静力计算结果，此时跌水闸闸室结构抗滑稳定安全系数Kc为2.30，满足安全需求；当该水平向地震惯性力朝上游时，结合静力计算结果，此时跌水闸闸室结构抗滑稳定安全系数Kc为4.64，满足安全需求。

表3 动静叠加下跌水闸闸室结构抗滑稳定计算分析表

3.5 抗震安全复核

综合上述计算结果，根据《水闸安全评价导则》（SL214-2015）［13］，跌水闸抗震安全满足《水工建筑物抗震设计标准》（GB51247-2018）要求，但存在不影响总体安全的缺陷，其抗震等级评定为B级。

4 结 论

基于有限元数值模拟技术，对某跌水闸闸室进行了抗震复核计算，根据计算结果，得到如下结论。

（1）正常蓄水位工况下，跌水闸闸室结构基频为3.57 Hz，其第一阶振型表现为启闭机房沿顺河向振动；

（2）跌水闸闸墩与闸底板相交处出现了2.00 MPa 拉应力，结合此处的配筋量，该处能承受的最大拉应力为4.41 MPa，满足安全需求；同时，跌水闸公路桥跨中底部位置出现了较大拉应力区，其数值远超混凝土动态轴心抗拉强度标准值，且桥梁底部钢筋混凝土出现了脱落、露筋和胀裂等情况，为安全起见，宜采取相应的抗震加固措施；

（3）地震作用最不利工况下，跌水闸闸室结构抗滑稳定安全系数为2.30，满足安全需求。根据《水闸安全评价导则》（SL214-2015），跌水闸抗震安全满足《水工建筑物抗震设计标准》（GB51247-2018）要求，但存在不影响总体安全的缺陷，其抗震等级评定为B级。