基于近场动力学理论的混凝土重力坝地震响应数值模拟

赵凯丽，邱流潮，李敬军

（中国农业大学水利与土木工程学院，北京100083）

0 引 言

随着国际能源发展战略方向的转移，大力发展水电等可再生能源成为了许多国家战略发展的新方向。我国如三峡水电站、糯扎渡水电站等大、中型水电站多数位于西部或西南部高烈度地震区［1］，地震作用下的安全问题是影响大坝可持续发展的重要因素，强烈地震作用下水工结构可能会产生结构破坏甚至垮塌的工程事故，从而造成人员伤亡、资金损失等一系列的灾难性后果。此外，我国大多数大坝都是在地震现场数据有限的情况下设计的［2］，大坝的除险加固研究也显得尤为重要。

随着计算机技术的高速发展，相较物理模型试验而言，数值模拟方法具有成本低、效率高、简单易行、可研究材料微观特性等一系列优点［3］，为大坝的地震动力响应研究提供了一种可行可靠的研究手段。在各种数值计算方法中，有限元方法的理论框架经过几十年的发展已相对较为成熟，在大坝的地震动力响应研究中被广泛应用［4-7］。然而，有限元方法是一种基于连续介质力学的方法，在求解非连续问题时仍存在局限性［5］，求解断裂破坏等非连续问题时会产生奇异性。针对上述不足，相关学者提出了一些改进方法，例如，Zhang 等［8］基于扩展有限元方法研究重力坝在地震作用下的裂纹扩展情况，Fang 等［9］应用扩展有限元方法模拟Koyna 大坝地震裂缝，该方法相对于有限元法有所改进，可以解决弱不连续问题，但是难以模拟多裂纹扩展问题。Das等［10］基于无网格法预测地震作用下大坝溃坝前破坏机制，该方法在处理网格畸变问题时具有很大优势，克服了对网格的依赖性，然而其计算量较大且在模拟多裂纹扩展时受到限制［11］。Pekau 等［12］基于非连续介质力学的离散元法对大坝进行裂缝分析，成功模拟了开裂问题，但是需要明确指出裂纹萌生点，在复杂的地震荷载作用下难以实现，并且计算量较大，因此需要一种新的方法来克服上述问题。

本文采用近场动力学（peridynamics，PD）方法进行混凝土重力坝地震响应数值模拟。该方法由美国Sandia 实验室的Silling［13］于2000年提出，黄丹等［14］2010年首次在国内应用。近场动力学法［15，16］是一种联系经典连续介质力学和分子动力学的数学力学理论，是分子动力学的连续版本，同时兼有分子动力学和无网格法的优点，在解决断裂等非连续大变形问题方面具有明显优势。近场动力学理论包括键基（bond-based）近场动力学理论和态基（state-based）近场动力学理论［17］，该理论已被应用到了许多研究领域，包括边坡稳定性分析［18］、非均质材料的水力压裂破坏模拟［19］、冰块撞击破坏［20］、岩土类材料［21］的大变形研究以及混凝土结构破坏过程模拟［22-24］等。Gu 等［25］运用近场动力学键基理论研究了混凝大坝冲击破坏；张钰彬等［26］模拟了高水头作用下混凝土重力坝的水力劈裂过程，为研究大坝破坏机理提供了新方法，具有重要的工程意义。

本文应用键基近场动力学理论对混凝土重力坝的地震动力响应进行了数值研究。论文的余下部分安排如下：在第一节中简要介绍了键基近场动力学理论及数值计算方法；在第二节中首先通过悬臂梁自由端施加集中力和底部输入周期运动的正弦波时的动力响应两个算例来验证模型和程序的精度和有效性，随后基于验证过的模型对混凝土重力坝的地震动力响应进行数值模拟；在第三节中列出了本文研究得出的一些结论和进一步研究的方向。

1 键基近场动力学方法

1.1 运动方程

近场动力学理论不再基于连续性假设以及微分方程求解力学问题［27］，而是采用非局部作用的积分形式的运动方程，避免了非连续奇异性问题的发生。非局部思想反映在物质的相互作用方面，如图1 所示，在某一时刻，空间域R内物体的任一物质点xi与以其为中心，近场范围δ（horizon）为半径的圆形平面或球体范围内的其他物质点xj之间产生相互作用，即当|xi-xj|≤δ时，两物质点之间产生相互作用力，而在近场范围内的物质点xj构成xi的家族（familiy），用H表示。

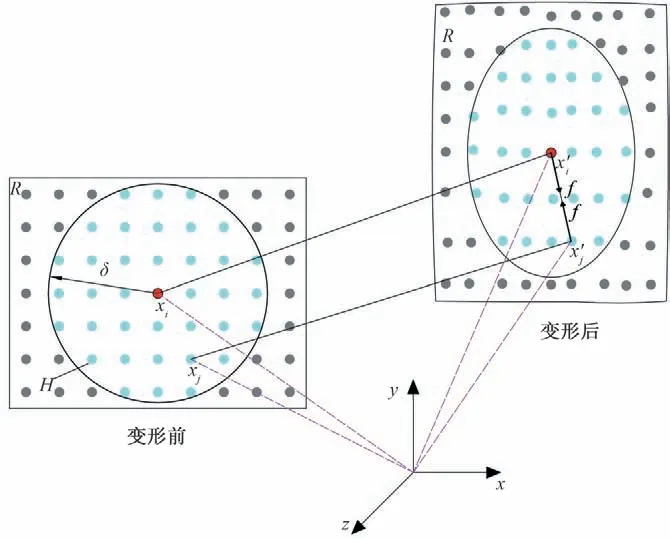
图1 物质点xi和xj变形过程中的相互作用Fig.1 Interaction between material points xi and xj during deformation

根据牛顿第二定律可以得到物质点xi的基于键基近场动力学理论的运动方程［28］：

式中：ρ表示密度；表示加速度；dV是物质点xj处的体积微元；b表示单位体积物质上施加的外部荷载，即体力密度为力的密度矢量，表示在t时刻物质点之间的相互作用。

对于键基近场动力学理论，物质点之间的相互作用力大小相等，方向相反，如图1所示。力密度矢量形式［29］如下：

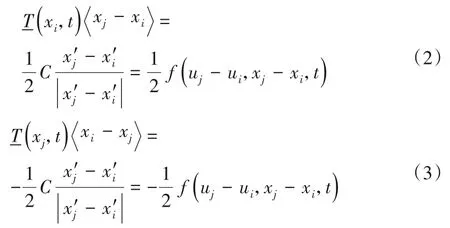
式中：C是一个与物质点xi和xj之间相对伸长量以及近场动力学范围有关的辅助参数和表示物质点xi和xj变形后的位置。则有物质点xi的运动方程为：

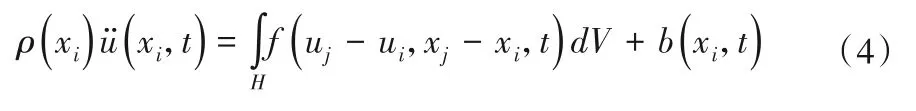
式中：f表示xi和xj之间的相互作用，用“键”来表示，由其构成的函数称作本构力函数。

两物质点之间的相对位置用ξ=xj-xi来表示，相对位移表示为：η=uj-ui，式（4）可进一步写为：

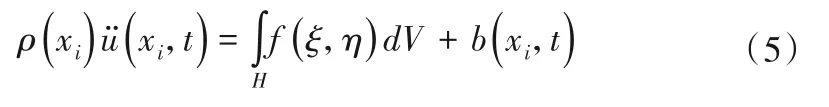
对于各向同性材料，可以假设力密度矢量f与物质点之间的拉伸成线性相关［29，30］：

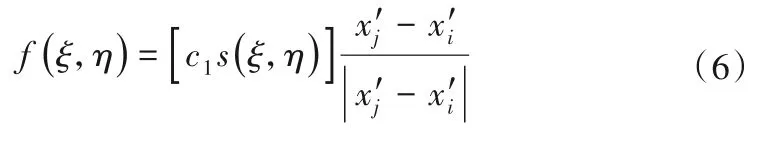
其中伸长率计算可以看做经典连续介质力学中的应变值计算如下［29］：

常数c1的计算公式如下［29］：

式中：c为键常数微观模量；体积模量，E是弹性模量，υ是泊松比。

1.2 数值离散与时间积分

近场动力学方法求解积分形式的运动方程，通常将所研究物体离散为一系列物质点，于是得到控制方程（4）在空间域的离散表达式为：

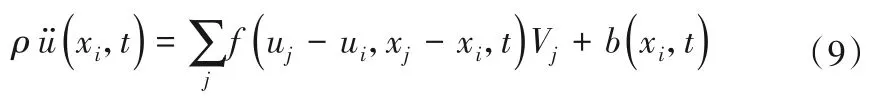
式中：Vj表示物质点xj代表的体积。

本文对（9）式采用显式的向前差分时间积分求解，即按下列步骤计算：

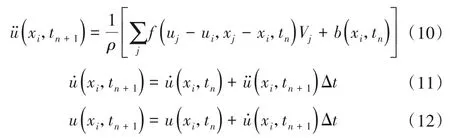
式中：n表示时间步数；Δt是时间积分步长，tn+1=tn+Δt，对于显式时间积分法，时间步长的选取需要满足稳定条件［30］。

2 数值算例与结果

本文通过使用FORTRAN 90 语言编程实现了近场动力学的数值计算。首先通过悬臂梁自由端受集中力响应以及在底部输入周期运动时动力响应两个算例验证来模型和程序的精度和有效性，接着对混凝土重力坝的地震动力响应进行了数值模拟。

2.1 集中力作用下的悬臂梁动力响应

这里首先对悬臂梁自由端在集中力作用下的动力响应进行模拟。悬臂梁的长度L=0.02 m，宽度W=0.002 m 和高度H=0.002 m，如图2 所示。悬臂梁自由端施加动荷载P随时间变化的关系如图3所示。

图2 悬臂梁尺寸及示意图（单位：mm）Fig.2 Dimensions and schematic diagram of cantilever beam

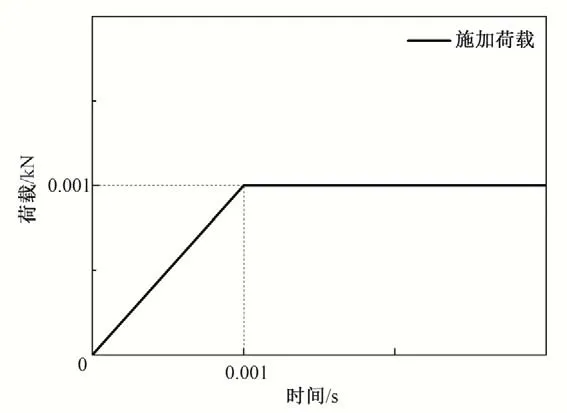
图3 荷载与时间之间的关系图Fig.3 The relation diagram between load and time

数值计算中，悬臂梁一共离散为337 50 个物质点，如图4所示。时间积分步长大小设置为Δt=1×10-8s，仿真总时间为0.02 s。本算例中使用的材料参数如下：密度为ρ=1 000 kg/m3，弹性模量E=1 GPa，泊松比为υ= 0.25。本算例将集中力作为体力密度施加在悬臂梁最外层单元上，并且暂时不考虑阻尼影响。

图4 悬臂梁初始时刻的离散效果图Fig.4 Discrete rendering of the cantilever at the initial moment

图5 给出了t=5×10-4s、t=2×10-3s、t=5.5×10-3s 和t=2×10-2s四个时刻悬臂梁的竖向位移云图。图6给出了悬臂梁自由端的竖向位移时程图，由于不考虑阻尼影响，1×10-3s 之后集中力大小不变时，自由端部数值模拟结果在1.5 mm 与2.5 mm 之间波动，即在解析解2 mm 上下波动，与实际相符，并将本文键基近场动力学模拟结果与有限元软件ABAQUS 的计算结果进行了比较，图6表明二者结果非常吻合，验证了本文键基近场动力学模型和程序的正确性。

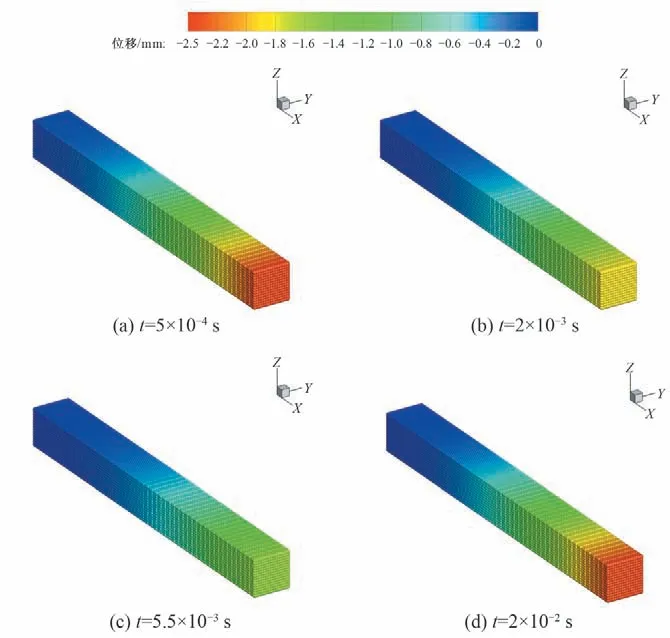
图5 悬臂梁在不同时刻z方向上的位移Fig.5 The displacement of the cantilever beam in the z direction at differenct moments

图6 自由端位移曲线比较Fig.6 The comparison of free end displacement curves

2.2 正弦加速度激励下垂直方柱的动力响应

在结构的地震动力响应分析中，需要输入地震波，本文计算中假设地基是刚性的，因而在结构基底输入地震加速度。本文近场动力学模拟中将已知加速度施加在三层虚拟边界层的物质点上实现地震波输入，虚拟边界层的定义如图7所示。

图7 虚拟边界层的定义Fig.7 The definition of virtual boundary layer

为了验证虚拟边界层物质点施加加速度模拟地震波的适用性和正确性，对垂直方柱在其底部正弦波激励作用下的动力响应进行数值模拟计算。方柱高度L=1.0 m，宽度W=0.02 m，厚度H=0.02 mm，如图8 所示。在本算例中，在方柱的底部虚拟边界三层粒子的y方向上施加总时长为4 s 的正弦加速度如图9所示。

图8 垂直悬臂柱体尺寸图（单位：m）Fig.8 The dimension of vertical cantilever column

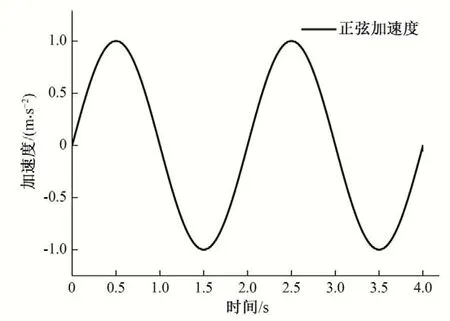
图9 正弦加速度Fig.9 Sinusoidal acceleration

数值计算中，方柱一共离散为10 800 个物质点，如图10 所示。时间积分步长大小设置为Δt= 1× 10-5s，仿真总时间为4 s。本算例中使用的材料参数为：ρ=7 780 kg/m3，弹性模量E=1 GPa，泊松比为υ= 0.25。计算中不考虑阻尼影响。

图10 垂直悬臂柱体离散图Fig.10 The discrete diagram of vertical cantilever column

图11 给出了t=1 s、t=2 s、t=3 s 和t=4 s 共4 个时刻方柱在y向位移云图，显示了柱体在施加周期波后在y方向上的摆动情况，且从图像可以看出悬臂柱体在以上4 个时刻顶部位移要大于底部位移，与图12 同一时刻相对应。图12 给出了方柱顶部和底部y向的相对位移时程图，更直观的显示出了柱体的动力响应，并将本文键基近场动力学模拟结果与有限元软件ABAQUS 的计算结果进行了比较，二者结果非常吻合，验证了本文基于键基近场动力学模型的虚拟边界层物质点施加加速度的方法实现地震波输入是可行的。

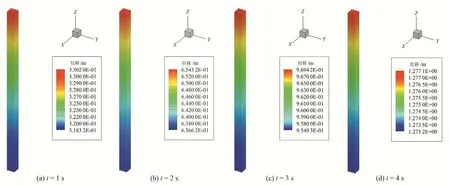
图11 悬臂梁在不同时刻y方向上的位移Fig.11 The displacement of the cantilever in the y direction at different moments

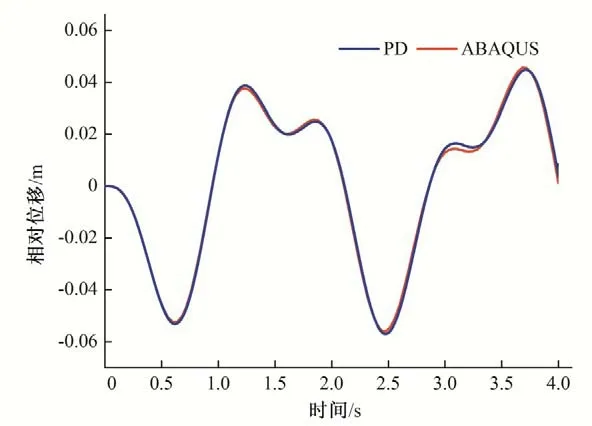
图12 近场动力学模型与ABAQUS软件计算得到的柱顶部和柱底部相对位移Fig.12 The relative displacement of column top and column bottom was calculated by the peridynamics model and ABAQUS software

2.3 混凝土重力坝地震动力响应

为了验证本文键基近场动力学模型模拟混凝土重力坝地震动力响应的可行性，本小节对Koyna 混凝土重力坝在水平及竖向地震波共同作用下的动力响应进行模拟。研究坝断面高度103 m，底宽70 m，顶宽14.8 m，原坝型形状及尺寸如图13所示。

图13 大坝基本尺寸示意图（单位：m）Fig.13 The schematic diagram of basic dam dimensions

数值计算中按照原坝型进行建模，为简化计算，将厚度方向取0.5 m，为一个单元高度大小，混凝土重力坝一共离散为28 840 个物质点，如图14 所示。时间积分步长大小设置为Δt=1× 10-5s，仿真总时间为10 s。本算例中使用的材料参数为：ρ=2 643 kg/m3，弹性模量E=31.02 GPa，泊松比为υ= 0.25。在本算例中，在坝的底部虚拟边界三层粒子的x及y方向上施加图15所示的地震加速度。计算不考虑库水及阻尼的影响，同时假设坝基为刚体。

图14 坝体离散图Fig.14 The discrete diagram of the dam

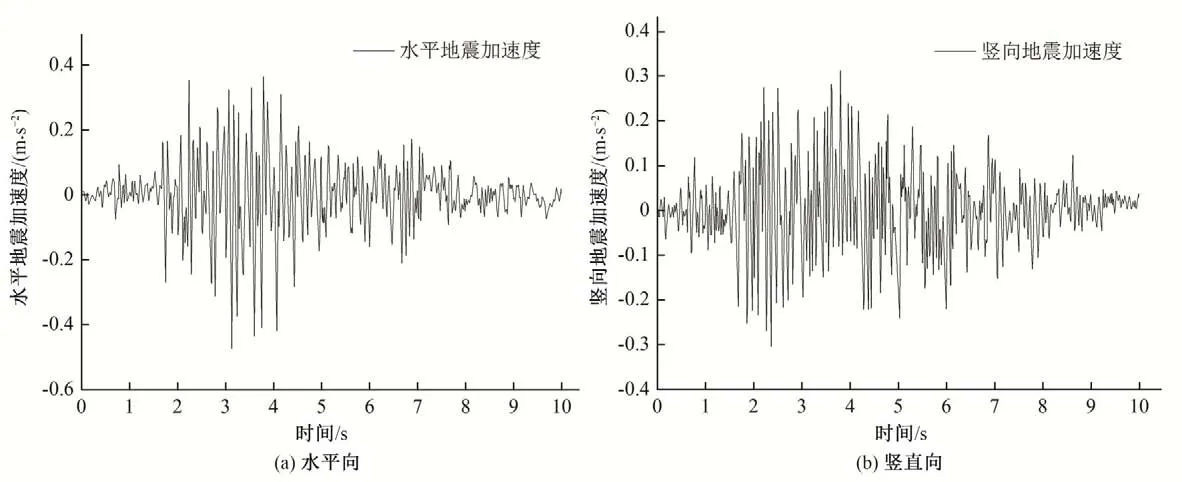
图15 地震加速度Fig.15 seismic acceleration

图16 和17 分别给出了t=2 s、t=4 s、t=8 s 和t=10 s 共4 个时刻混凝土坝水平向和竖向位移云图。图18 给出了混凝土重力坝顶水平向和竖向相对位移时程图的键基近场动力学模拟结果，数值计算中采用键基近场动力学模型在虚拟边界层物质点施加加速度的方法实现地震波输入，从图像可以看出，坝体的各个部位在不同方向上的动力响应情况随时间是变化的，由于本模拟厚度方向上取一个单元厚度，故暂不考虑z方向上的动力响应情况。从图18可以看出大约在3 s左右坝体横向和纵向位移开始有明显波动，与施加的地震波波动大小相对应，很好说明了本文键基近场动力学模型模拟混凝土坝地震动力响应是可行的。

图16 重力坝在不同时刻沿x方向的位移Fig.16 The displacement of the gravity dam in the x direction at different moments

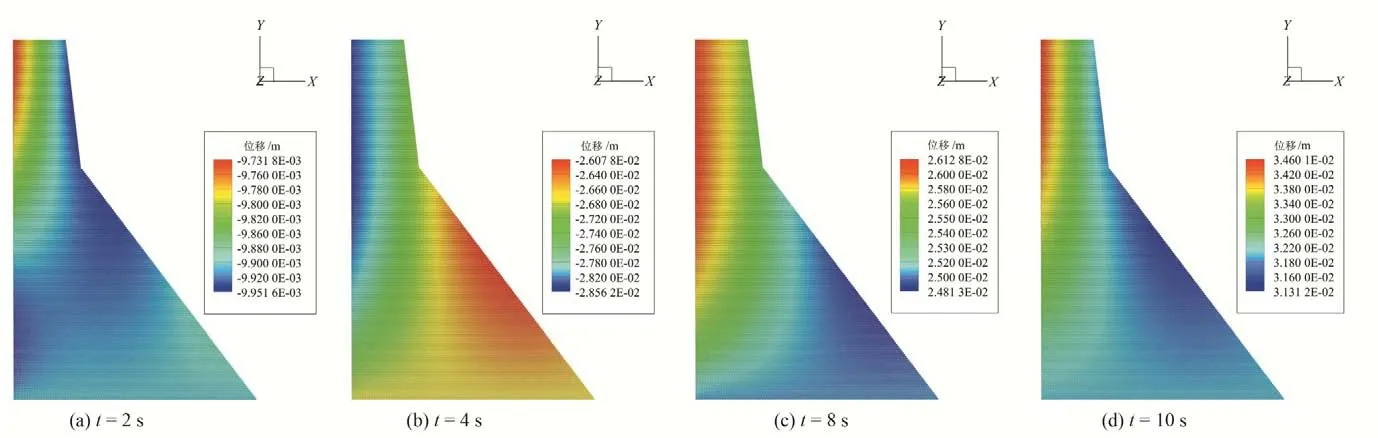
图17 重力坝在不同时刻沿y方向的位移Fig.17 The displacement of the gravity dam in the y direction at different moments

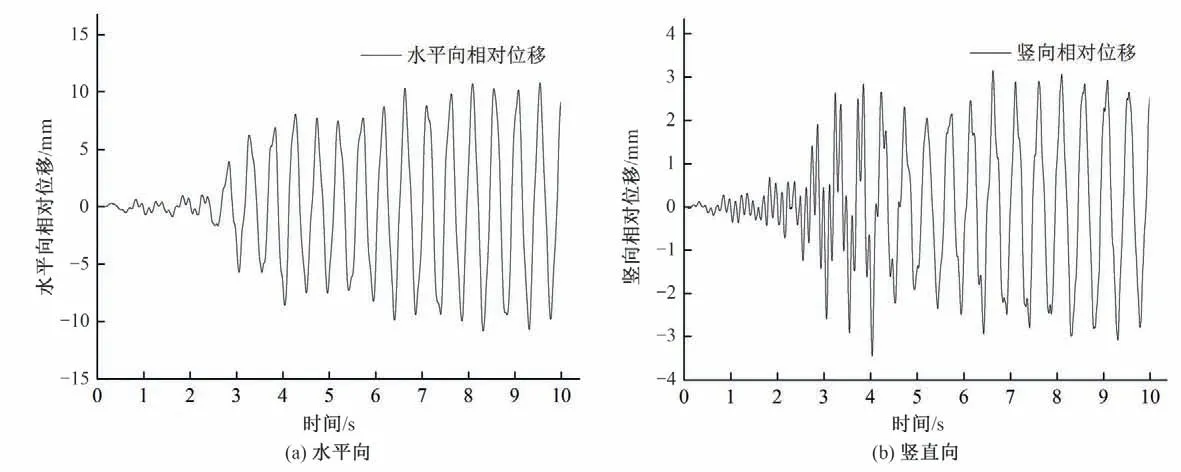
图18 坝顶相对位移时程图Fig.18 The relative displacement time history of dam crest

3 结 论

本文建立了模拟混凝土重力坝地震动力响应的键基近场动力学模型，并采用FORTRAN90语言编程实现。其中，地震波的输入是通过在三层虚拟节点施加地震加速度来实现的。本文通过对比悬臂梁自由端和底部受动力和周期运动正弦波的近场动力学数值模型与ABAQUS 软件的模拟结果，证明该近场动力学模型适宜模拟动力响应问题。接着利用本文模型对混凝土重力坝的地震动力响应进行数值模拟，结果表明：本文键基近场动力学模型模拟混凝土重力坝的地震动力响应是可行的，为混凝土坝地震动力响应数值模拟方法提供了新的思路。

近场动力学需要计算近场范围内的所有物质点的相互作用，较有限元等传统的网格方法需要计算的物质点多，因此计算时间较长，今后有待于进一步开展并行算法研究以提高计算效率。本文选用较为简单、应用较广的近场动力学键基模型，存在泊松比的限制，一些情况下可能产生误差，后续可以采用态基近场动力学模型进行研究。另外，本文计算中没有考虑坝基的变形以及辐射阻尼的影响，将在后期研究中进一步考虑。